Готови сте да задълбаете знанията си в статистическия анализ с Excel, специално в областта на анализа на разпределението. В този урок ще научите как да количествено определите и сравните колебанията в оборота за различни категории продукти като смартфони и лаптопи. Ще използвате различни статистически показатели, за да ефективно установите наличните разлики и вариации. Този анализ може да ви предостави ценни познания и да подкрепи вашето вземане на решения в рамките на управлението на продуктовият портфейл.
Най-важните изводи
Анализът на колебанията в оборота показва колко силно оборотите на даден продукт се различават от средното им. Ще изчислите основни статистически показатели като дисперсия, стандартно отклонение и коефициент на вариация. Тези показатели помагат за оценка на стабилността на оборотите и предоставят сравнителни стойности между различни продукти.
Стъпка по стъпка насоки
Стъпка 1: Подготовка на данните
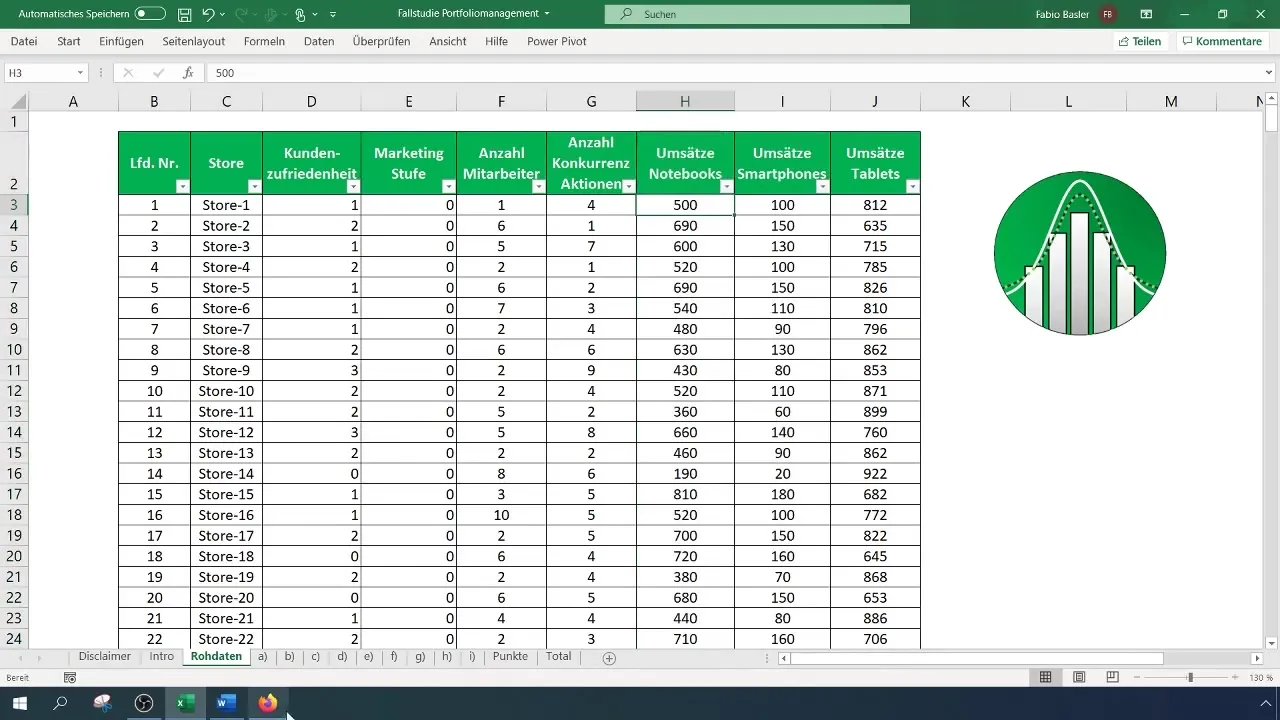
За да можеш да извършиш анализа коректно, данните ти трябва да бъдат структурирани. Увери се, че разполагаш с данни за оборота на смартфони и лаптопи в един Excel документ. Започни, като копираш данните в две отделни колони, за да осигуриш прегледност.
Стъпка 2: Изчисляване на средна стойност
Следващата стъпка е да изчислиш средната стойност на оборотите за двете категории продукти. Използвай формулата =СРЕДНОГР(). Тази стойност ще ти даде първоначална представа за средния оборот, който всеки продукт може да постигне.
Стъпка 3: Изчисляване на дисперсията
Дисперсията количествено оценява разпръснатостта на оборотните стойности. Можеш да я изчислиш с формулата =ДИСП.P(). За изборка използвай формулата =ДИСП.S(). По-висока стойност показва по-големи отклонения на отделните стойности от средната им стойност.
Стъпка 4: Изчисляване на стандартното отклонение
Стандартното отклонение е квадратният корен на дисперсията. В Excel можеш да я изчислиш с формулата =СТАНДО.П(). Тя показва колко силно отделните стойности отклоняват около средната си стойност.
Стъпка 5: Определяне на коефициента на вариацията
Коефициентът на вариация (VK) е относителна мярка, която определя стандартното отклонение спрямо средната стойност. Изчисли го с формулата =СТАНДО.П() / СРЕДНОГР(). Висока стойност на VK показва големи колебания спрямо средната стойност.
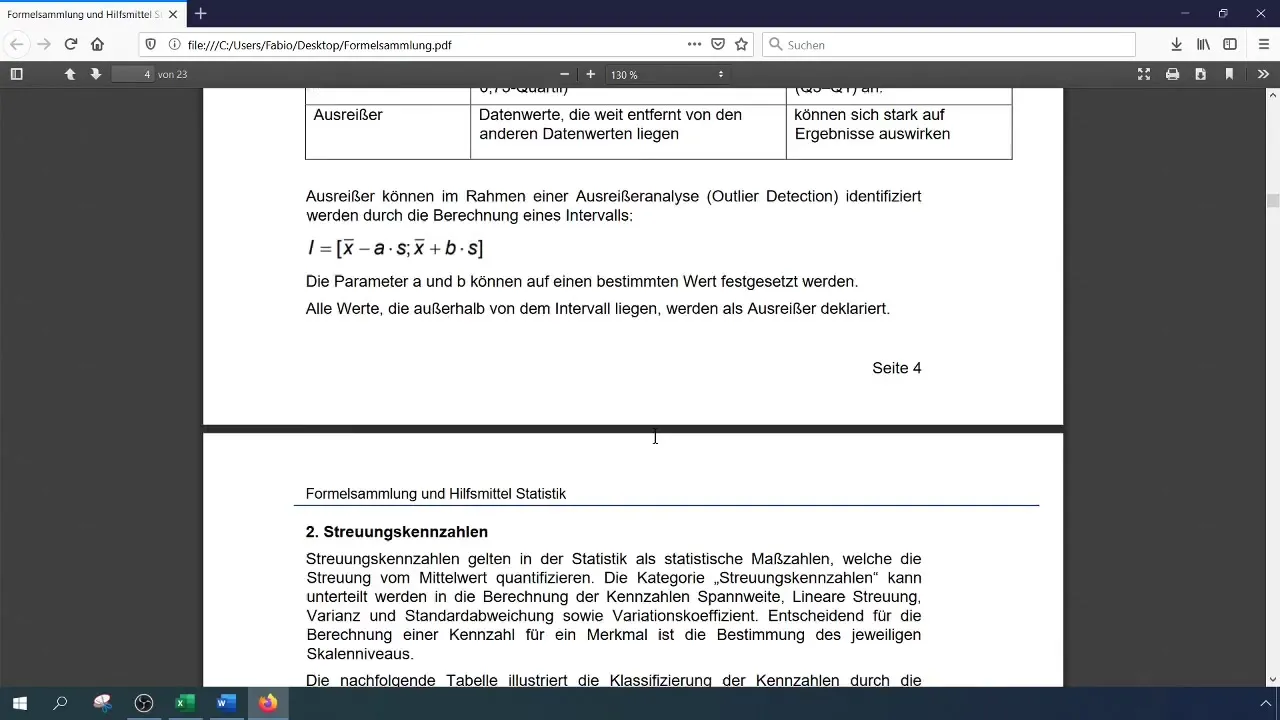
Стъпка 6: Анализ и интерпретация на резултатите
След като изчислиш показателите, анализирай резултатите. Висок коефициент на вариация (например ≥ 0,65) е индикатор за големи колебания в оборота. Обърни внимание и на конкретните отклонения в данните си, които могат да доведат до тези колебания.
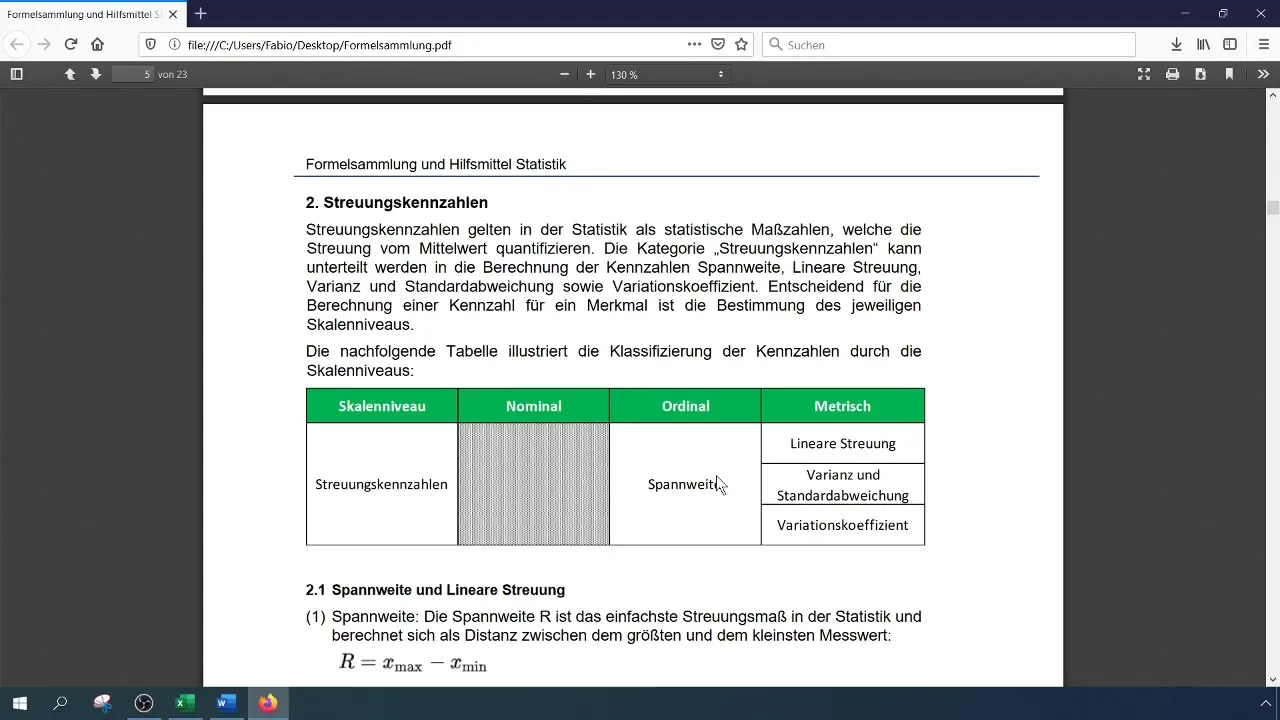
Стъпка 7: Използване на сводни таблици
Ако искаш преглед на изчисленията си, можеш да използваш и сводни таблици. Избери си си суровите данни, отиди в меню „Поставяне“ и избери „Сводна таблица“. Сводната таблица ти позволява да представиш оборотните данни по-структурирано и предлага автоматични изчисления на средни стойности и стандартни отклонения.
Стъпка 8: Приспособяване на изчисленията в сводните таблици
В рамките на сводната таблица можеш да промениш настройките така, че получиш средна стойност и стандартно отклонение на оборотите. Щракни с десния бутон на мишката в полето на сводната таблица и избери „Настройки на стойностното поле“. Там можеш да избереш, че за оборотите ще бъде изчислена средната стойност, за да постигнеш ясна представа.
Стъпка 9: Потвърждаване на ръчното изчисление
Имай предвид, че коефициентът на вариация не може да бъде изчислен директно в сводни таблици. Вместо това трябва ръчно да изчислиш стандартното отклонение спрямо средната стойност, което ти дава възможност да потвърдиш последователността на стойностите си и тук.
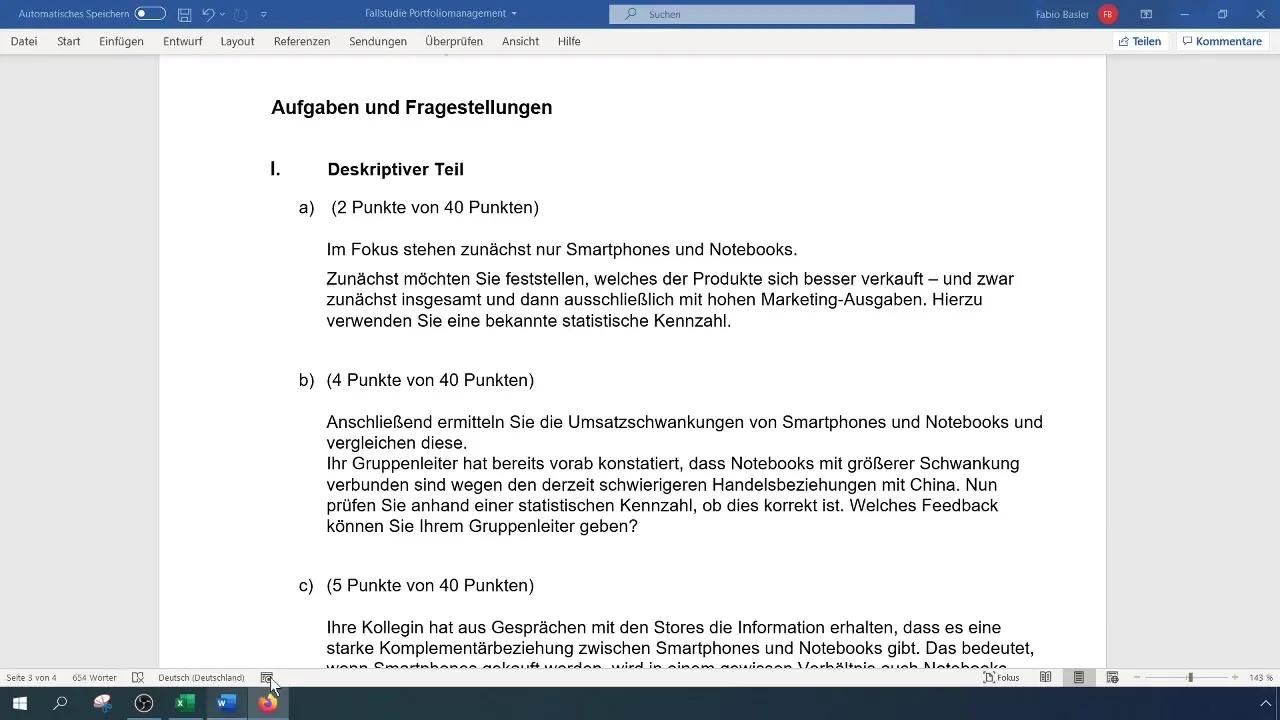
Стъпка 10: Обратна връзка и документация
Събери резултатите си в кратка документация. Увери се, че включваш основните точки от анализа си, както и всякакви отзиви или специфични забележки от ръководителя на групата ти.
Резюме
В това ръководство научи как да анализираш колебанията в оборота на смартфони и лаптопи, използвайки основни статистически мерки като средно аритметично, дисперсия, стандартно отклонение и коефициент на вариацията. Виждаш как можеш да ги изчислиш в Excel и как можеш да продължиш анализа си чрез пивот-таблици. Резултатите ще ти помогнат да вземеш обосновани решения в областта на управлението на продуктите.
Често задавани въпроси
Как се изчислява средно аритметично в Excel?Можеш да изчислиш средно аритметично с формулата =СРЕДНОВРАТИЕ(Обхват), където „Обхват“ указва клетките, които съдържат данните ти за оборота.
Каква е разликата между дисперсията и стандартното отклонение?Дисперсията измерва разпръскването на стойностите, докато стандартното отклонение е корен квадратен от дисперсията и представя разпръскването в същите единици като оригиналните данни.
Мога ли да изчисля коефициентите на вариация в пивот-таблици?Не, коефициентът на вариация не е директно наличен в пивот-таблици. Трябва да го изчислиш ръчно, като разделиш стандартното отклонение на средното аритметично.
Какво означават високите коефициенти на вариация?Високите коефициенти на вариация (например ≥ 0,65) указват на силни колебания на оборотните стойности в сравнение със средното.
Как мога да идентифицирам аутлайърите в моите данни?Можеш да идентифицираш аутлайърите, като изолираш колебанията и провериш дали еднoчлeннитe cтойности значително cе различават от средната стойност.


