Статистическите тестове са централна част от анализа на данни и вземането на решения. Особено в областта на биотехнологиите може да бъде от съществено значение да се проверят хипотези за успеваемостта на активните съставки. В рамките на този урок ще научите как да използвате ефективно тест за една извадка (1-SP-тест) за очакваната стоиност с известна дисперсия в Excel.
Най-важни изводи
Този указател ще ви помогне да:
- Теоретичните основи на 1-SP-теста.
- Стъпки за изпълнение на теста в Excel.
- Интерпретация на резултатите.
Подготовка на данните
За да извършите теста за една извадка в Excel, първо трябва да разполагате със съответните данни. В нашия пример предполагаме ситуация, в която анализирате успеваемостта на активните съставки. Известно е, че средната успеваемост преди е била 59%, със стандартно отклонение от 19. Първоначално трябва да въведете данните си в таблица на Excel.
Уверете се, че данните са организирани в колони, така че по-късно да можете да им достъпвате. Добрата организация ще ви помогне да разберете лесно отделните стъпки.
Преглед на теста
1-SP-тестът служи за проверка дали средната стойност на успеха се различава значително от предварително зададената стойност. В този случай проверяваме дали успеваемостта от 59% може значително да се увеличи в бъдеще.
Формулиране на хипотези
Формулирането на хипотезите, които задавате за теста, е от съществено значение:
- Нулева хипотеза (H0): Истинската очаквана стойност е равна на 59 (σ = 59%).
- Алтернативна хипотеза (H1): Истинската очаквана стойност е по-голяма от 59%.
При формулирането на хипотезите вниманието трябва да бъде фокусирано върху това, какво точно трябва да бъде тествано и как това се отразява в контекста ви.
Важно е ясно да разпознаете разликата между нулевата и алтернативната хипотеза, тъй като те представляват базата за следващите изчисления.
Събиране на извадката
За нашия тест вземаме извадка от 500 активни съставки. Важно е да се отбележи, че изборът на извадката трябва да бъде репрезентативен и гарантиран по съответния начин, за да може резултатите ви реалистично да се приложат за цялата популация.
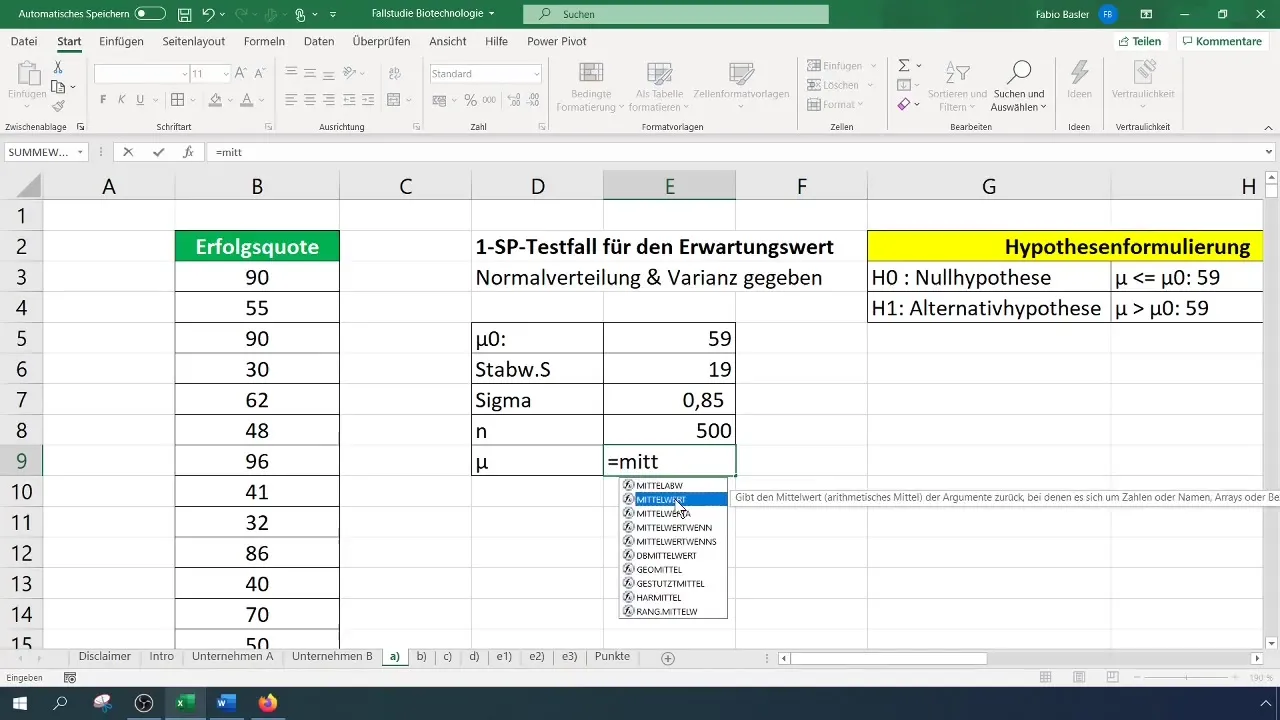
За теста първо трябва да пресметнете средното аритметично. Това може лесно да се направи, като използвате съответната формула в Excel.
Изчисляване на тестовия размер
Тестовият размер за 1-SP-тест се определя чрез следната формула:
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Тук (\bar{x}) представлява средната стойност на вашата извадка, (\mu_0) е предполаганата средна стойност (в този случай 59), (\sigma) е стандартното отклонение (тук 19), и (n) е броят на извадките (500).
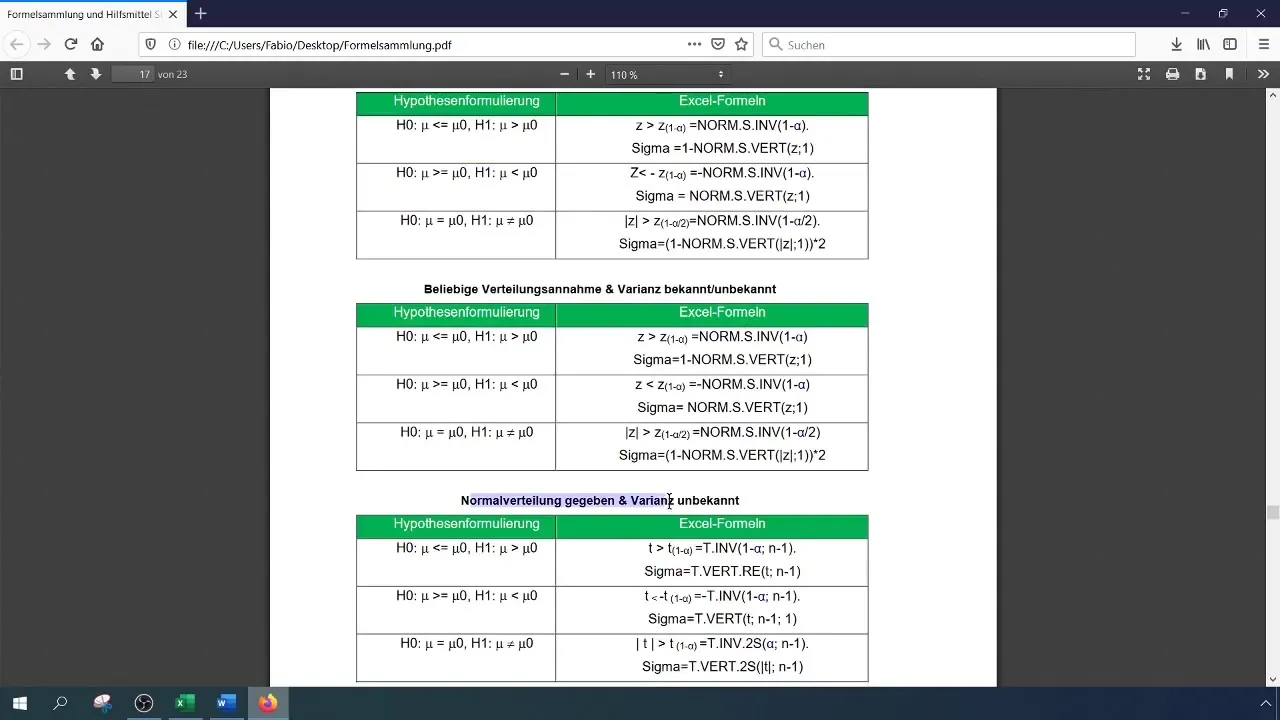
След като вкарате стойностите във формулата, пресметнете тестовия размер, за да определите дали е значим или не.
Установяване на критичната стойност
За значимост от 1% (0,01) трябва да прочетете или изчислите критичната стойност. Можете да направите това в Excel, използвайки функцията NORM.S.INV.
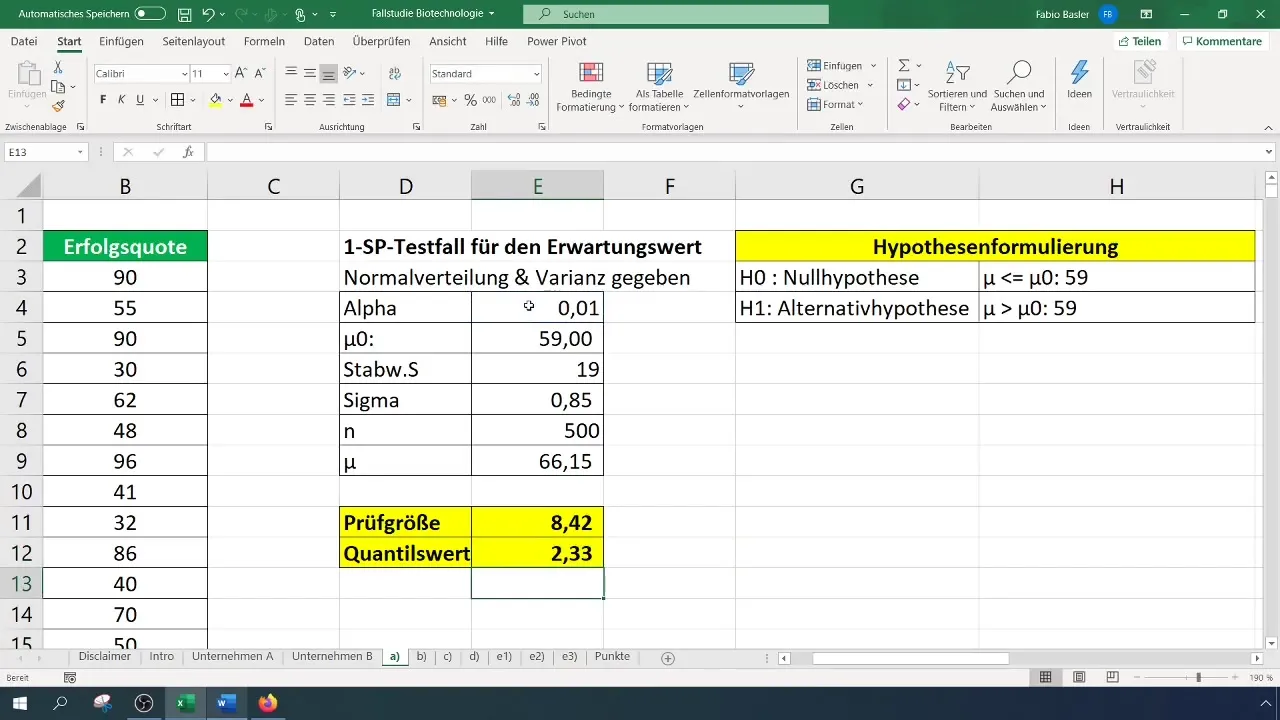
Формулата е:
[ \text{NORM.S.INV}(1 - \alpha) ]
Тук (\alpha) е нивото на значимост (0,01). Получената стойност ще бъде основата за сравнението с тестовия размер.
Изпълнение на теста
След като вече разполагате и с тестовия размер, и с критичната стойност, сравнете ги:
- Ако тестовият размер е по-голям от критичната стойност, нулевата хипотеза се отхвърля.
- В противен случай не може да се отхвърли нулевата хипотеза.
В нашия случай се получава стойност на теста от 8,4, която надвишава критичната стойност от 2,33. Затова можем да отхвърлим нулевата хипотеза. Това указва, че процентът на успешност е значително подобрен.
Интерпретация на резултатите
След като извършиш теста и определиш резултатите, трябва да ги интерпретираш в ясен контекст. Отхвърлянето на нулевата хипотеза означава, че тестваната нова стойност се различава значително от миналото, в този случай от 59%.
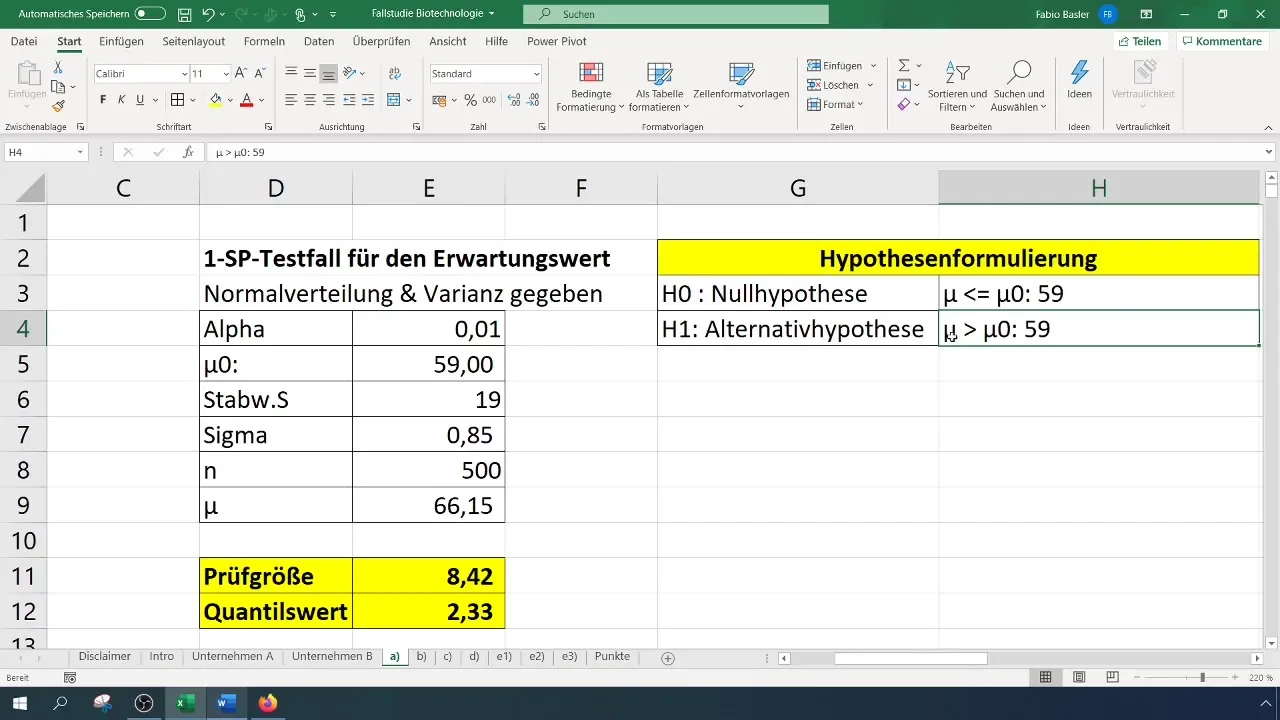
Тази информация е от огромно значение за стратегическото вземане на решения във вашия бизнес. Те потвърждават, че усилията за подобряване на процента на успешност бяха ефективни.
Резюме
В този урок научихте как да извършите тест за очакваната стойност в Excel с един стандартен пробен тест. Чрез казусна студия успяхте да следвате стъпките от формулирането на хипотезите през изчислението на данните до интерпретацията на резултатите. Този тип познания не са важни само за научни изследвания, но и за практически приложения в бизнеса.
Често задавани въпроси
Какво е тестът с един стандартен пробен тест?Тестът с един стандартен пробен тест е статистически тест, който проверява дали средната стойност на извадката се различава значително от предварително зададена стойност.
Какъв е начинът на поставяне на хипотезите за този тест?Хипотезите включват нулева хипотеза (H0) и алтернативна хипотеза (H1), които документират състоянието, което трябва да се провери.
Как се пресмята тестовата стойност?Тестовата стойност се определя по формулата ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ).
Какво се случва, ако тестовата стойност е по-голяма от критичната стойност?Ако тестовата стойност е по-голяма от критичната стойност, нулевата хипотеза се отхвърля.
Каква е ролята на нивото на значимост?Нивото на значимост показва с каква вероятност сте готови да приемете грешка, ако отхвърлите погрешно нулевата хипотеза.


