Двустранният тест на двата избора-t е важен инструмент в статистиката, когато искате да изследвате разликата между две средни стойности. В този урок ще научите как да извършите този тест лесно и ефективно в Excel. Чрез пример от биотехнологията ще научите как да сравнявате и статистически анализирате успешностите на две конкуриращи се компании.
Най-важните изводи
- Прилагане на двустранния t-тест за анализ на разликата между две средни стойности.
- Формулиране и проверка на хипотези.
- Използване на Excel за изчисляване и представяне на резултатите.
Стъпково ръководство
Първоначално започваме със създаването на необходимите данни и извършването на тест в Excel.
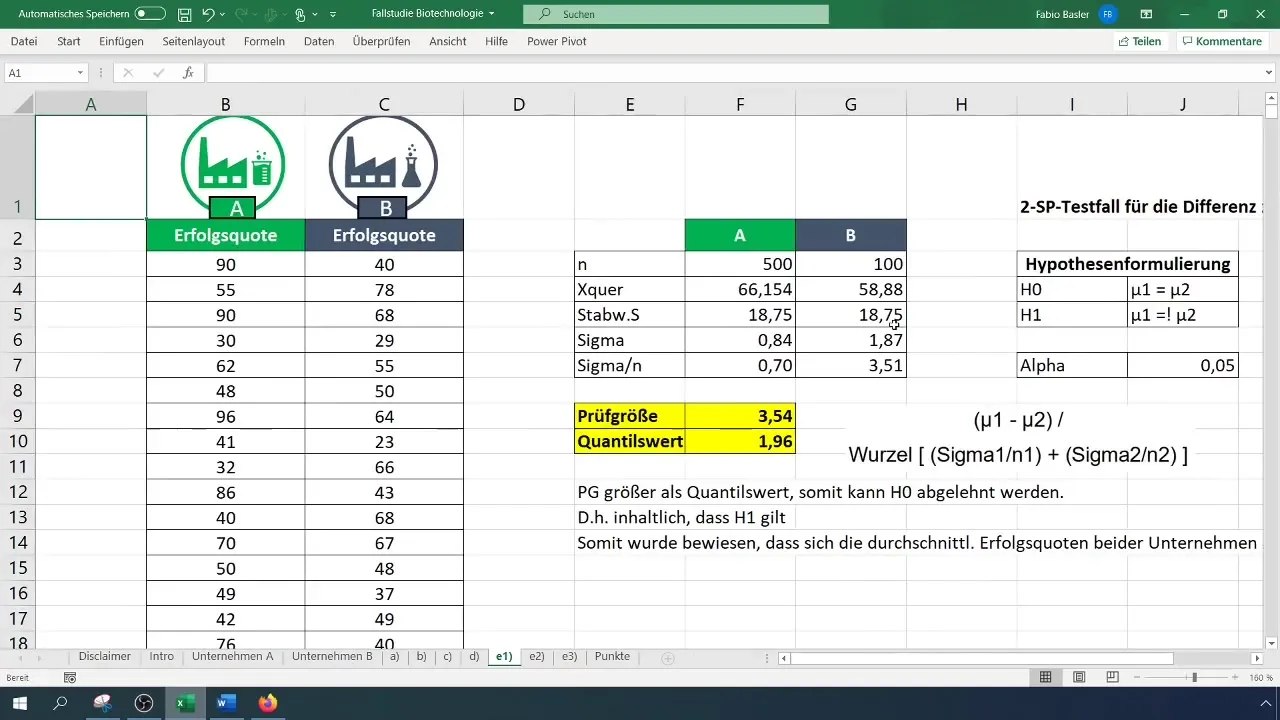
Стъпка 1: Подготовка на данните
Започнете събирането на суровите данни за успеха на двете компании. Нека предположим, че разполагате с данни за компания A и B. За всяка компания имате изборка от 100 записа.

Стъпка 2: Изчисляване на обема на изборката и средните стойности
Създайте таблица в Excel, за да сравните изборките и техните средни стойности. Първоначално изчислете обема на изборката (N) за двете компании, както и средната стойност (X).

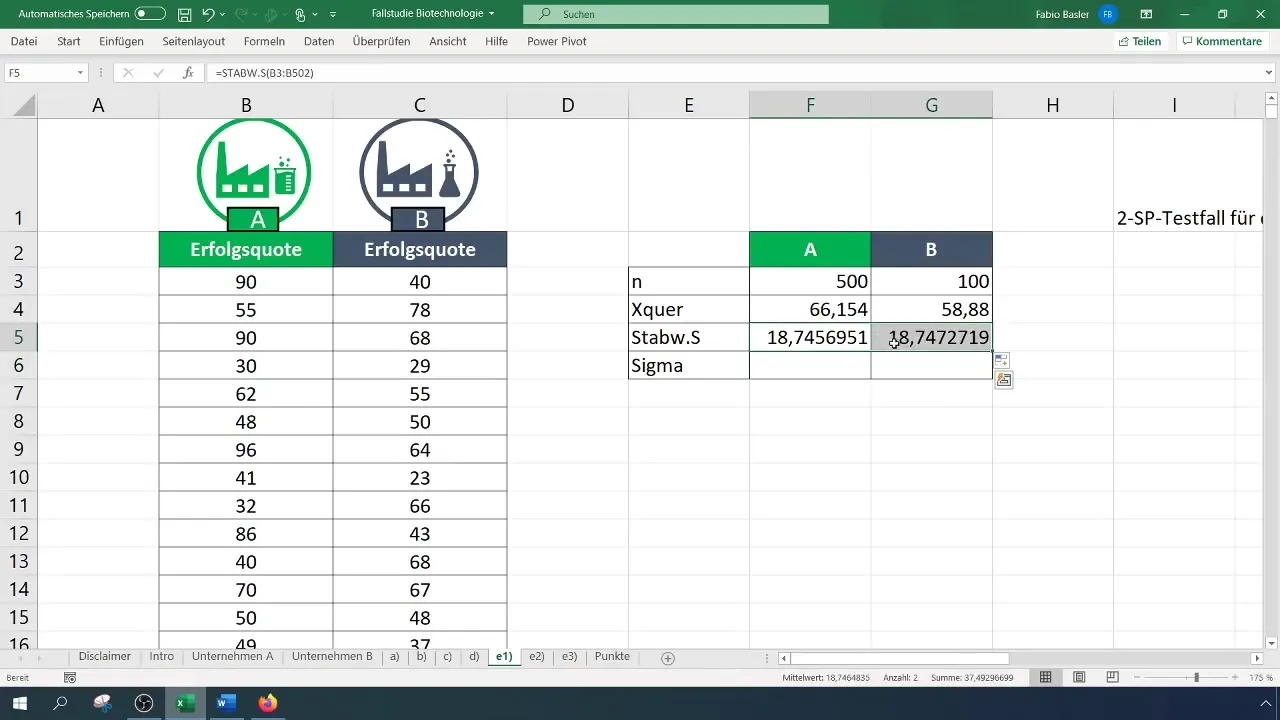
Стъпка 3: Определете стандартните отклонения
Изчислете стандартното отклонение за двете компании. Тези стойности са важни за извършване на изчисления по отношение на дисперсията и следващите стъпки.
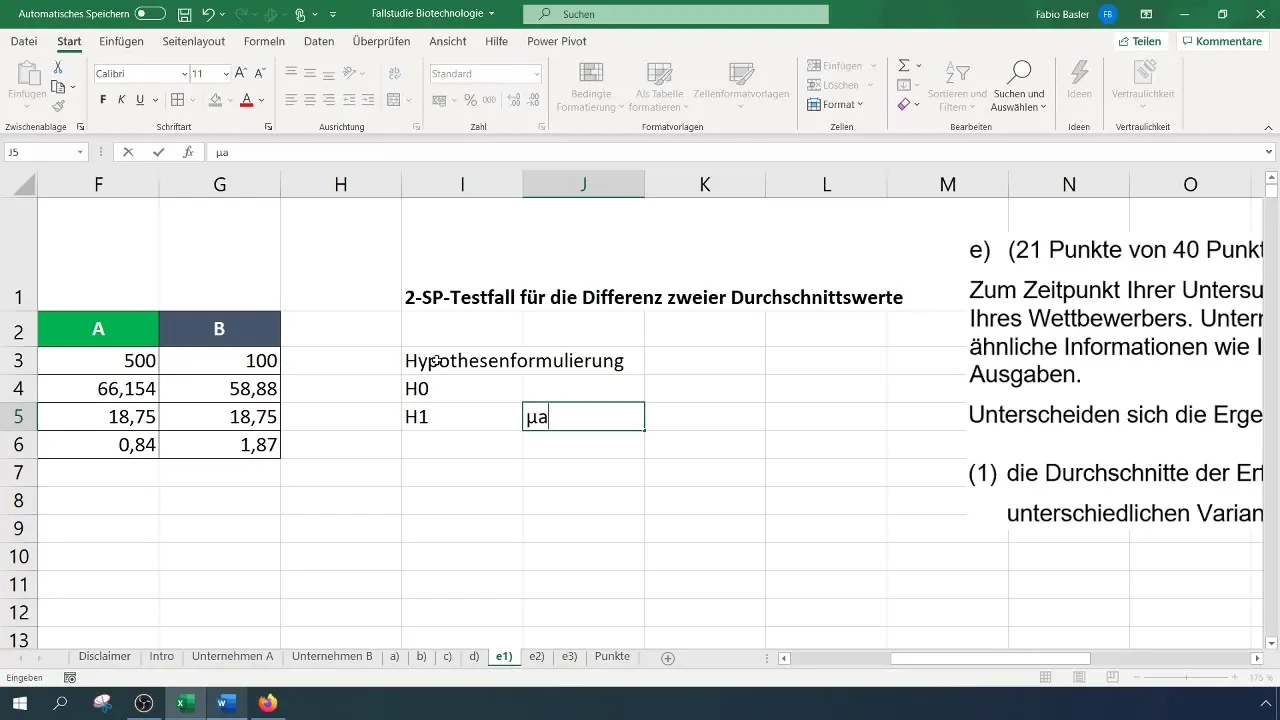
Стъпка 4: Формулиране на хипотези
Формулирайте нулевата хипотеза (H_0): Средните стойности на успеха на компаниите A и B са еднакви. Алтернативна хипотеза (H_1): Средните стойности на успеха са различни.
Стъпка 5: Изчисляване на статистическата величина
За изчисляването на статистическата величина използвайте формулата за t-тест. Изчислете разликата на средните стойности и разделете на квадратния корен на сумата на дисперсиите на всяка изборка.
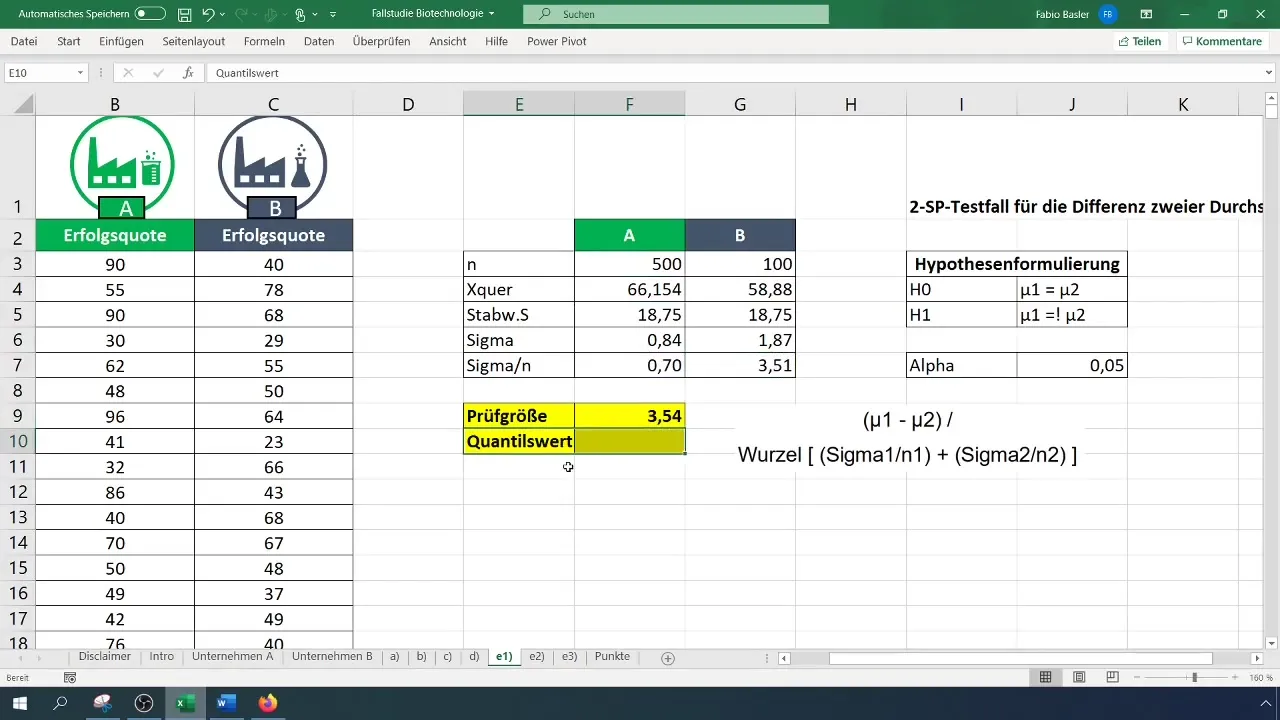
Стъпка 6: Определете критичната стойност
Използвайте двустранното t-разпределение, за да намерите критичната стойност. Задайте нивото на алфа на 0,05. Проверете таблицата на t-разпределението или изчислете фактора директно в Excel.
Стъпка 7: Вземете решение за хипотезата
Сравнете изчислената статистическа величина с критичната стойност. Ако статистическата величина е по-голяма от критичната стойност, отхвърлете нулевата хипотеза (H_0) и така потвърдете алтернативната хипотеза (H_1).
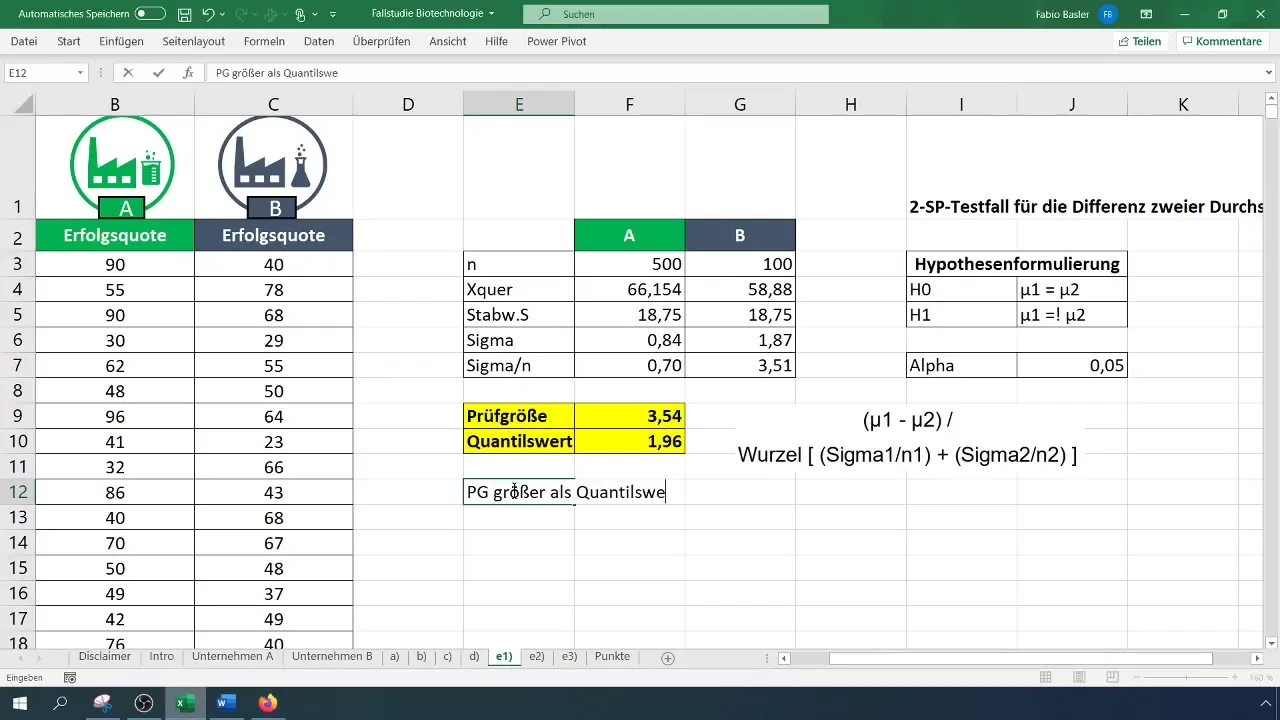
Стъпка 8: Интерпретация на резултата
Накрая интерпретирайте резултата. В този пример средните успехи на двете компании бяха установени като значително различни.
Обобщение
Научихте как да извършите двустранен тест на двата избора в Excel, за да изследвате разликите в средните стойности на две групи. Стъпките от подготовката на данните през формулирането на хипотезите до интерпретацията на резултатите са ключови за приемане на валидни и информирани решения.
Често задавани въпроси
Какво е двустранният тест на двата избора?Двустранният тест на двата избора сравнява средните стойности на две групи, за да определи дали те са значително различни.
Как да формулирам хипотези?Нулевата хипотеза (H_0) твърди, че средните стойности са равни, докато алтернативната хипотеза (H_1) твърди, че те са различни.
Как се изчислява статистическата величина?Статистическата величина се изчислява чрез деление на разликата на средните стойности на квадратния корен от сумата на дисперсиите.
Какво следва след изчисляването?Сравнете статистическата величина с критичната стойност, за да решите дали можете да отхвърлите нулевата хипотеза.
Защо е важно стандартното отклонение?Стандартното отклонение помага за разбиране на вариабилността на данните, която е от решаващо значение при изчисляването на статистическата величина.


