Хи-квадрат адаптационен тест за нормално разпределение с Excel

Хипотезният тест за пригодност на хи-квадрат представлява прост метод за проверка на хипотезата дали даден набор от данни следва нормално разпределение. В това ръководство ще научите как да използвате Хи-квадрат теста в Excel, за да установите дали оборотите на смартфони следват нормално разпределение. Ще преминем стъпка по стъпка през процеса, започващ от създаването на класифицирана таблица на честотите до изчисляването на статистиката на теста и сравняването й с критичната стойност на хи-квадрат.

Най-важни изводи

• Тестът за пригодност на хи-квадрат помага за проверка на нормалните разпределения.
• Важно е да се създаде класифицирана таблица на честотите.
• Статистиката се сравнява с критична стойност, за да се приеме или отхвърли нулевата хипотеза.

Стъпка по стъпка ръководство

Стъпка 1: Подготвяне на данните

За да извършите Хи-квадрат теста, първо ще ви трябват данни. Копирайте оборотите на смартфоните в един лист в Excel. Уверете се, че данните ви са организирани в една колона.

Стъпка 2: Създаване на хистограма

За да получите първите визуални показатели за разпределението, създайте хистограма на данните си. За целта отидете в „Вмъкни“ и изберете „Диаграми“. Добавете хистограма, като изберете областта за данните си.

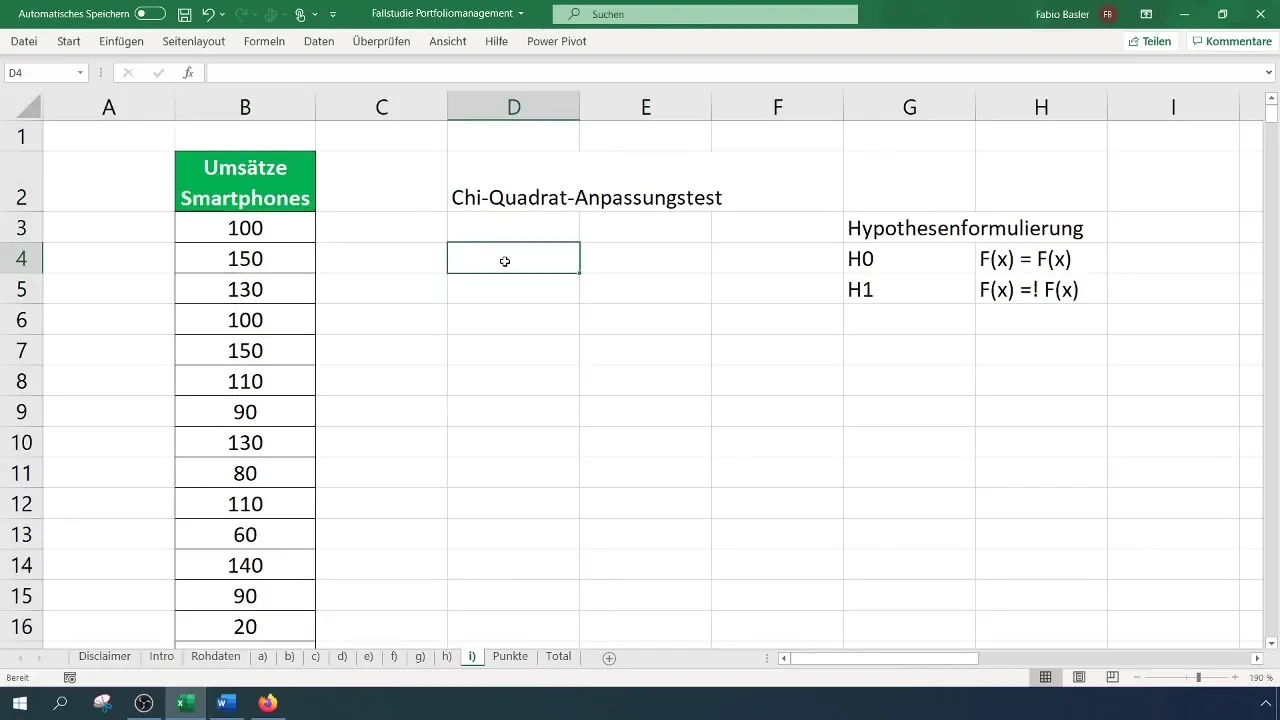
Стъпка 3: Създаване на класирана таблица на честотите

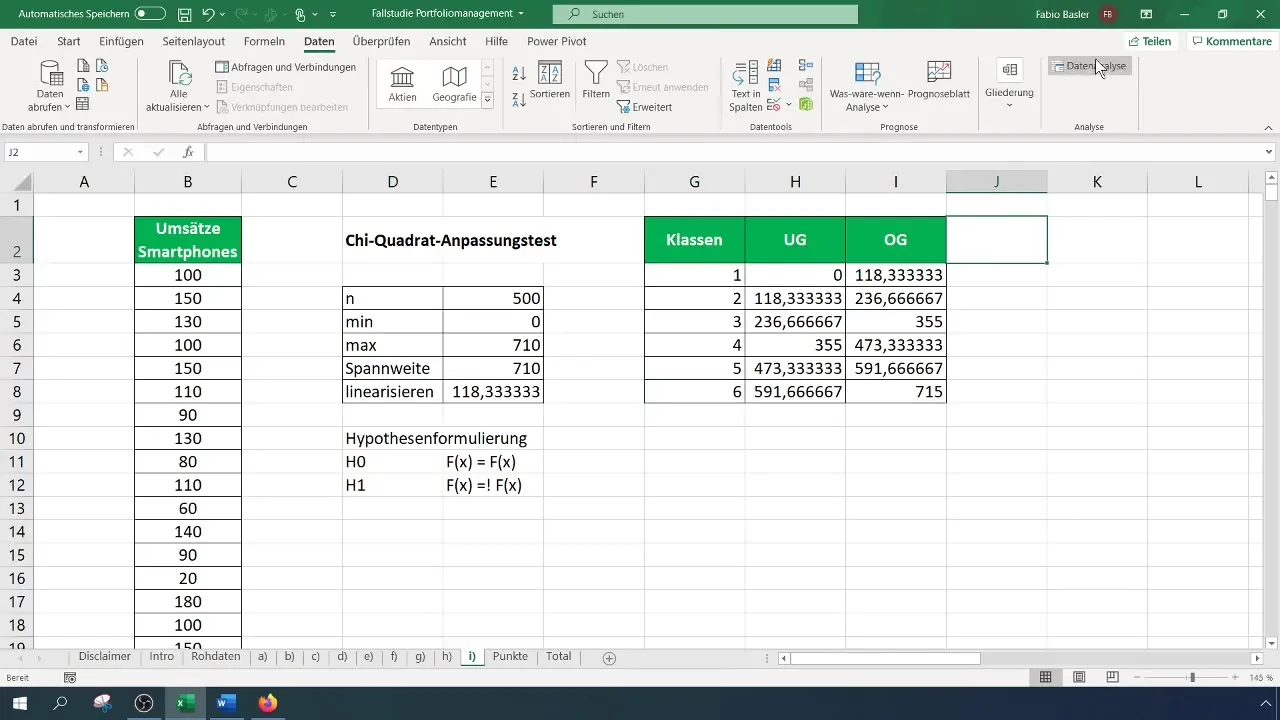
За Хи-квадрат теста е необходима класифицирана таблица на честотите. Определете първо броя на класовете за таблицата си – в този случай използваме шест класа. Пресметнете ширината на интервалите и създайте таблицата съответно.

Стъпка 4: Пресмятане на честотите

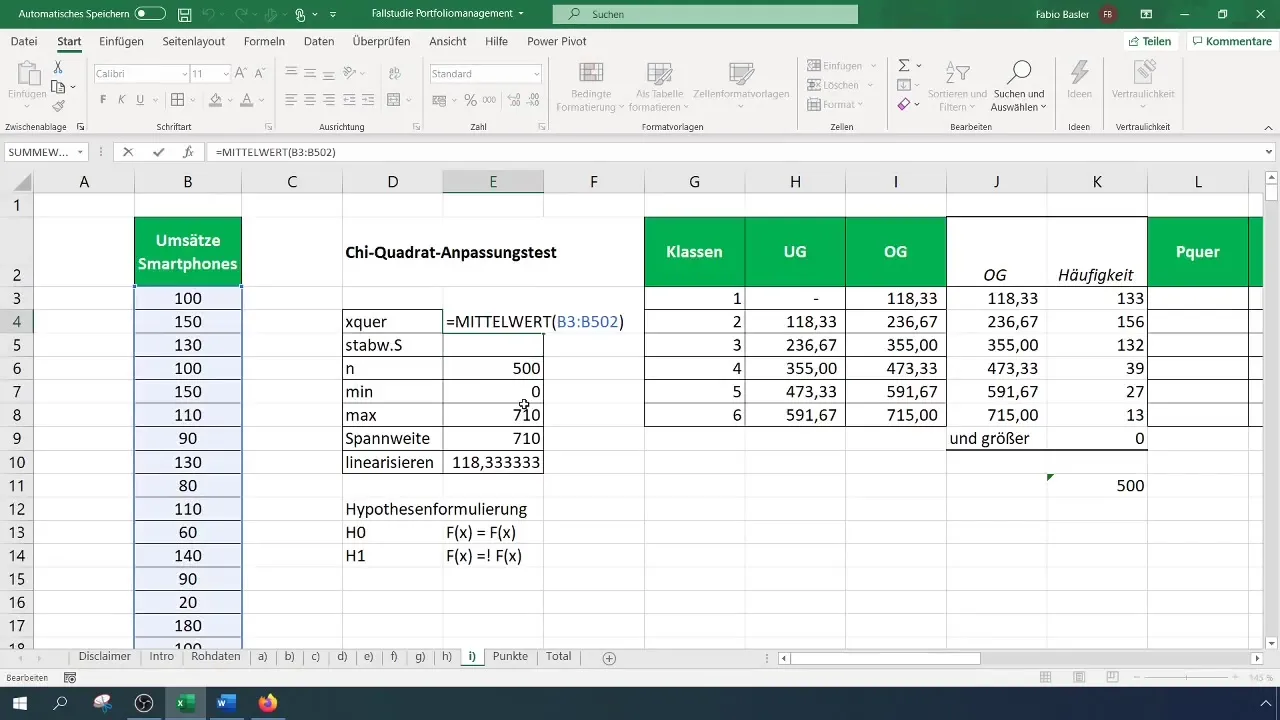
Сега трябва да пресметнете качествата за всяка класа. Отидете в „Анализ на данните“ от менюто и изберете „Хистограма“. Изберете входната област за вашите данни и класните граници. Определете изходната област за таблицата на честотите.

Стъпка 5: Пресмятане на очакваните честоти

За да определите очакваните честоти, пресметнете вероятностите за всяка класа, базирайки се на предположеното нормално разпределение. За тази цел е необходима средноаритметическата стойност и стандартното размах на вашите данни.

Стъпка 6: Пресмятане на статистиката на теста

Пресметнете статистиката на теста (Хи-квадрат) с формулата:

[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]

където (O_i) са наблюдаваните, а (E_i) очакваните честоти. Можете да извършите тази пресмятане в Excel, като запазите отделните компоненти в отделни клетки.

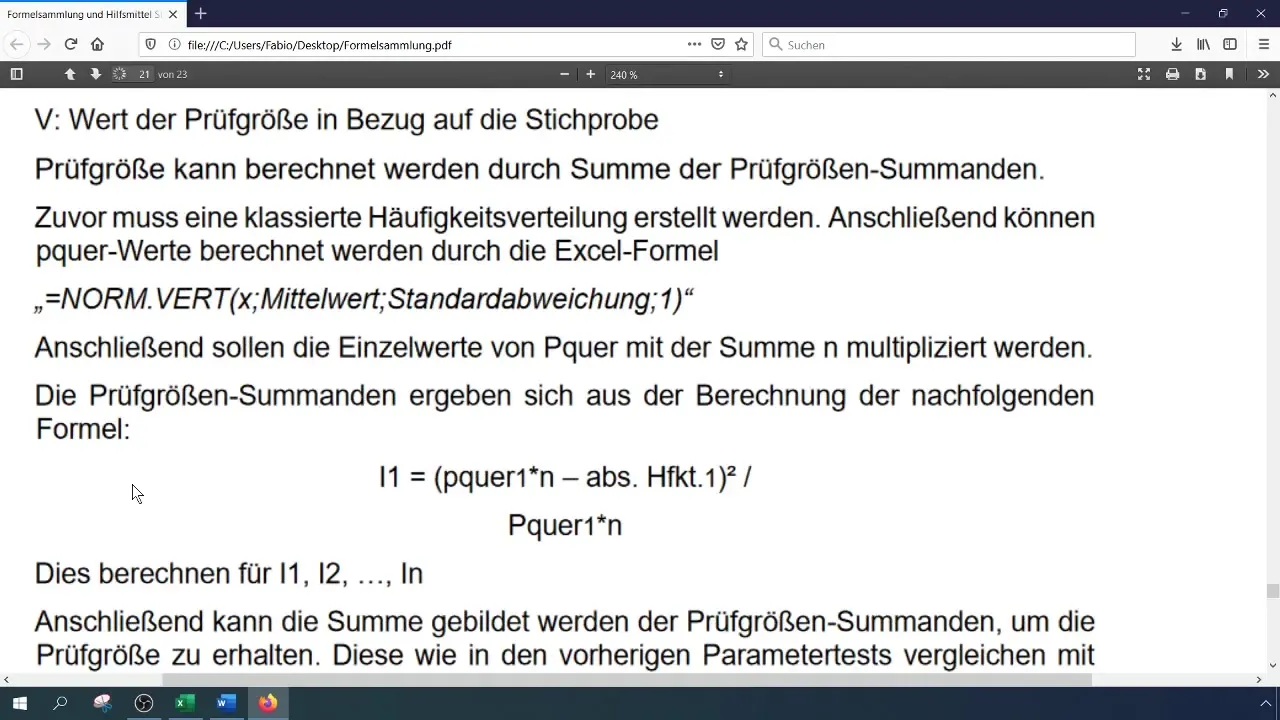
Стъпка 7: Пресмятане на критичната стойност

За да оцените статистиката на теста, трябва да пресметнете критичната стойност ( \chi^2 ) за вашето ниво на доверие и броя на степените на свобода. Броят на степените на свобода за Хи-квадрат теста е (k - 1), където (k) е броят на класовете.

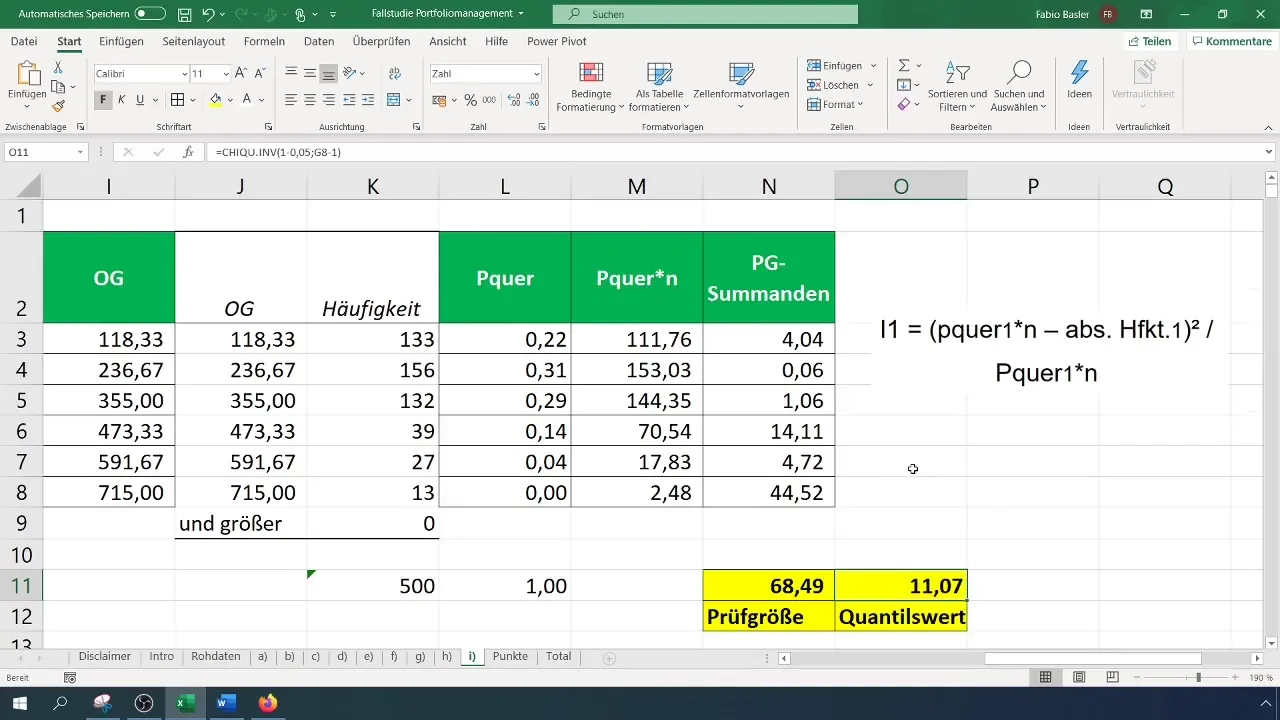
Стъпка 8: Проверка на хипотезите

Сравнете пресметнатата статистика на теста с критичната стойност. Ако статистиката на теста е по-голяма от критичната стойност, отхвърлете нулевата хипотеза, което означава, че данните не са нормално разпределени. В противен случай приемете нулевата хипотеза.

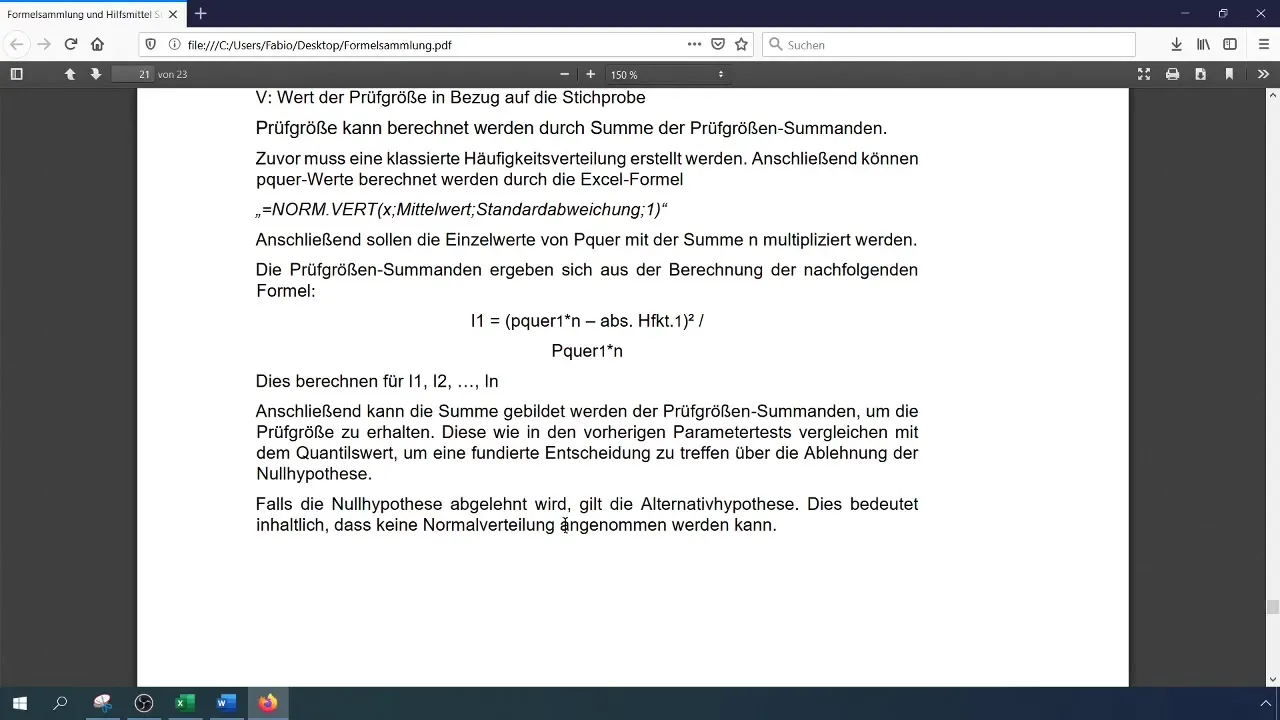
Стъпка 9: Сборяем резултатите

Запиши резултатите си и ги разшири с графичните данни и хипотезните тестове. Не забравяй да провериш хистограмата си, за да потвърдиш визуално, че разпределението не е нормално.

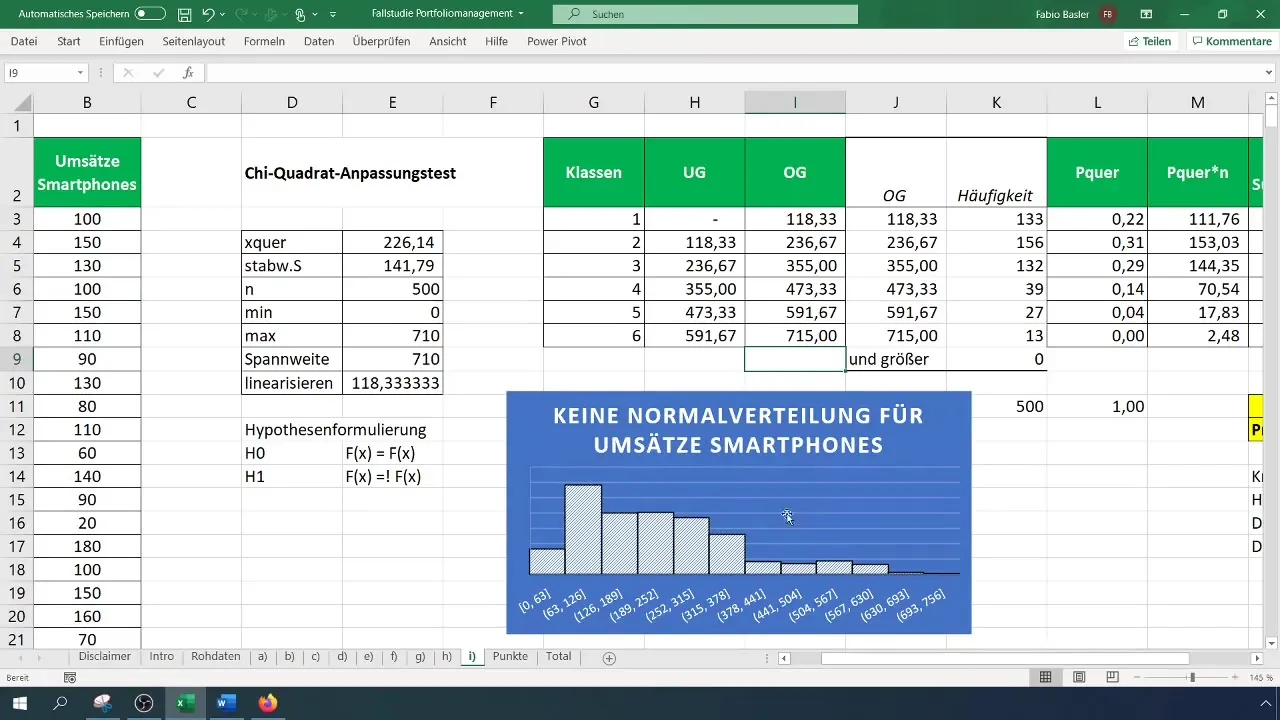
Обобщение

През този урок научихте как да използвате теста на приспособеност на квадрата на Хи в Excel, за да анализирате нормалното разпределение на приходите от смартфони. Стъпките включват създаване на класифицирана таблица с честотата, изчисляване на очакваните честоти, проверката и, накрая, сравнението с критичната стойност.