Статистическите анализи са незаменимо средство в управлението на портфейла. Една особено мощна процедура е анализът на регресията, особено когато става въпрос за определяне на влиянието на няколко независими променливи върху една зависима променлива. Искаш ли да разбереш как можеш да построиш и анализираш линеен функционален свързан модел чрез множествена регресия в Excel? Този наръчник ти предоставя ясен преглед и подробно стъпково ръководство.
Най-важни изводи
- Анализът на регресията помага да се количествено измери влиянието на независимите променливи върху една зависима променлива.
- Важно е да се оцени качеството и статистическата значимост на модела за регресия.
- Чрез оценяване на кофициентите може да се определи коя от независимите променливи оказва по-силен влияние върху зависимата променлива.
Стъпково ръководство за анализ на регресия в Excel
Подготовка на данните
Преди да започнете анализ на регресия, трябва да подготвите данните си. Зависимата променлива (у) в този случай е оборотът на ноутбуките, а независимите променливи (x1 и x2) са броят на служителите и броят на конкурентните акции. Първо трябва да въведете всички необходими данни в Excel и да ги представите по ясен начин.
Проверка на корелацията
За да получите първите показатели за евентуални връзки между променливите, можете да създадете корелационна матрица. Тази матрица ви помага да видите колко силно са свързани различните променливи помежду си. Можете да го направите чрез функцията "Анализ на данни" в Excel и след това да изберете корелационната матрица, като включите всички релевантни области на данните.
Изпълнение на анализ на регресията
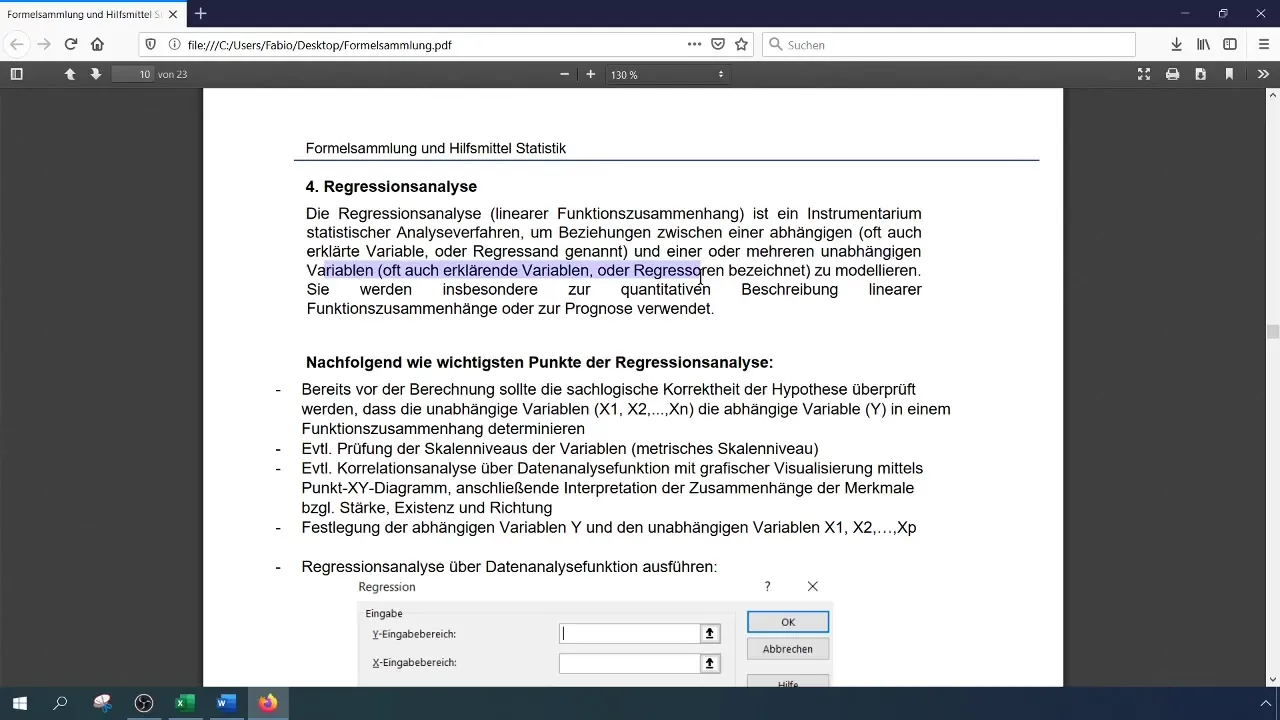
Сега сте готови да изпълните анализ на регресията. Изберете отново функцията "Анализ на данни", след което изберете "Регресия". Тук определете областта на входните данни за зависимата променлива (оборотът на ноутбуките) и независимите променливи (брой на служителите и конкурентните акции).
Интерпретация на резултатите
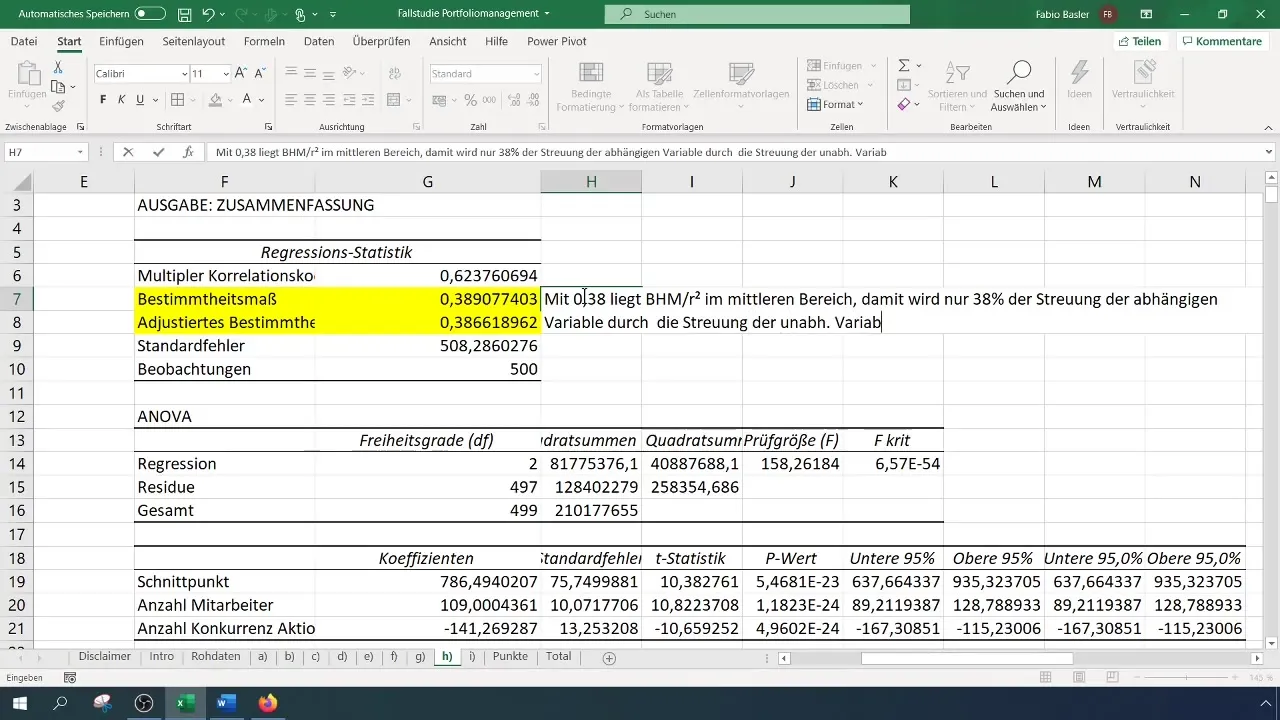
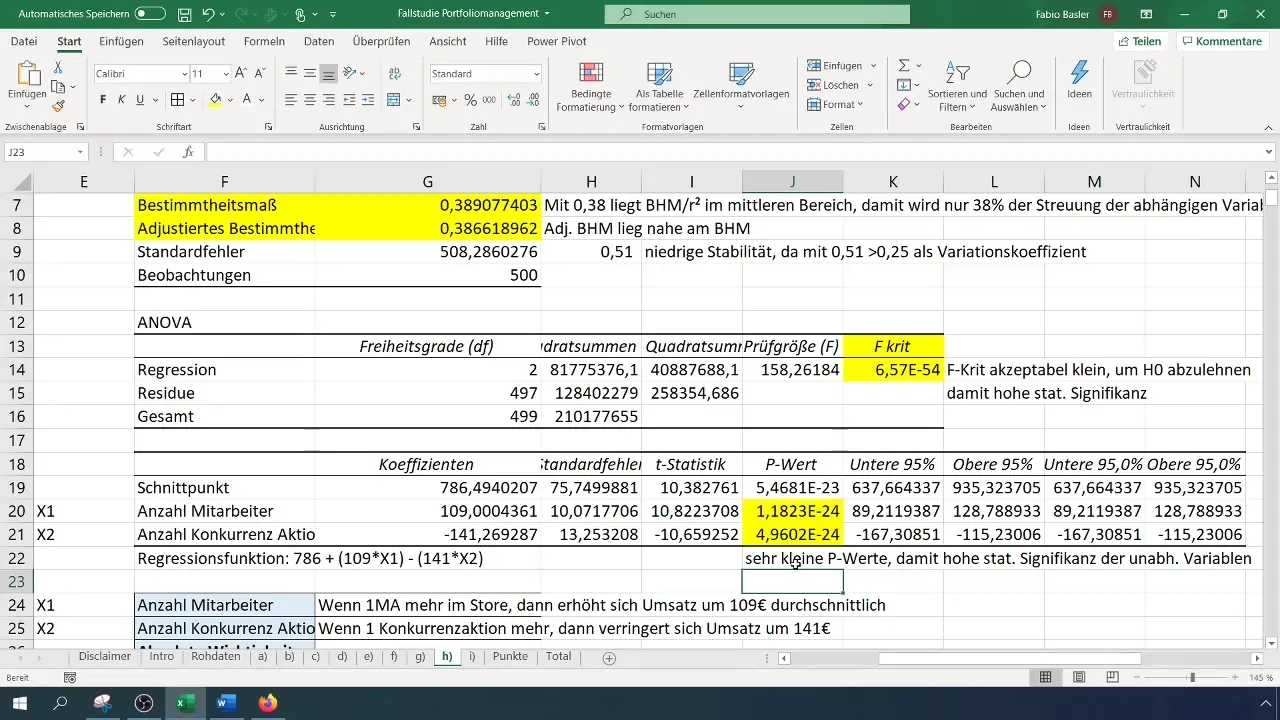
След изпълнение на анализ на регресията ще получите множество изходи и статистики. Първият важен аспект е мерата на детерминираност (R²), която описва процента от обяснението на зависимата променлива от независимите променливи. Стойността на R² от 0,38 показва, че 38% от вариативността в оборота може да бъдат обяснени от двете независими променливи.
При оценяването трябва да обърнете внимание на това колко стабилен е моделът. Можете да използвате стандартната грешка, за да определите стабилността. Например, ако получите стандартна грешка от 0,51, това означава висока относителна промяна и по-ниска стабилност.
Оценка на силните фактори за влияние
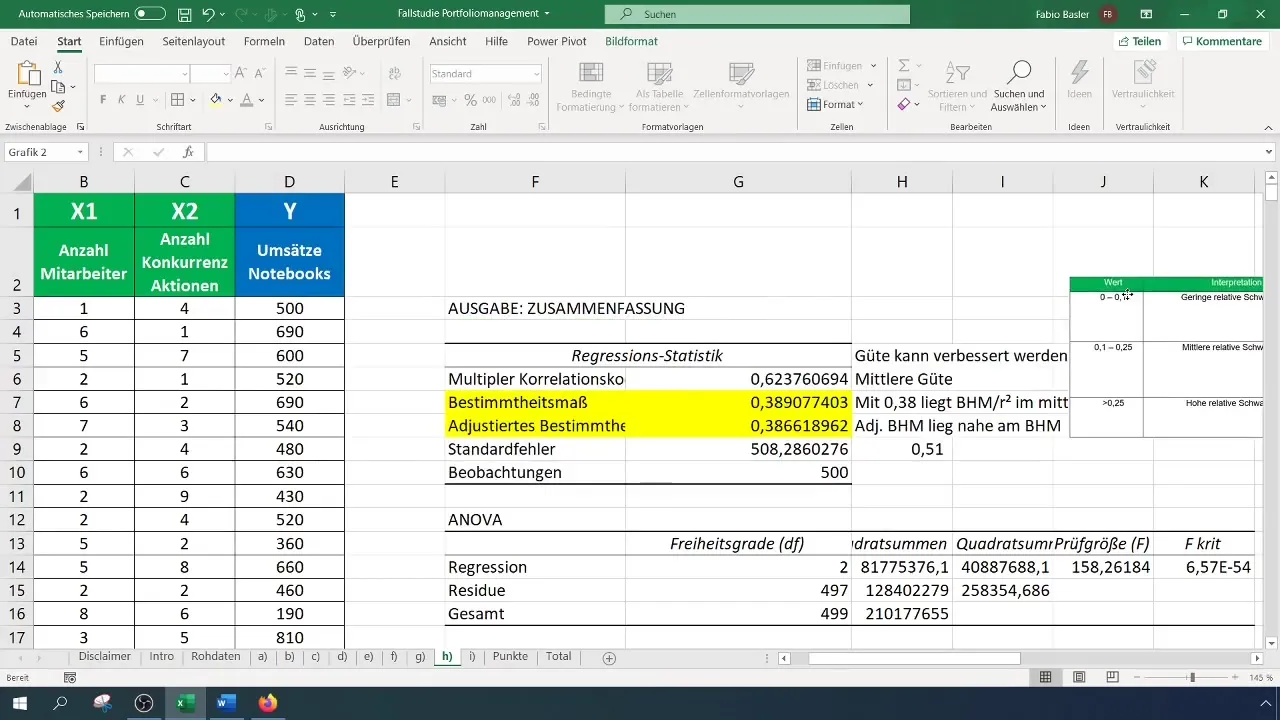
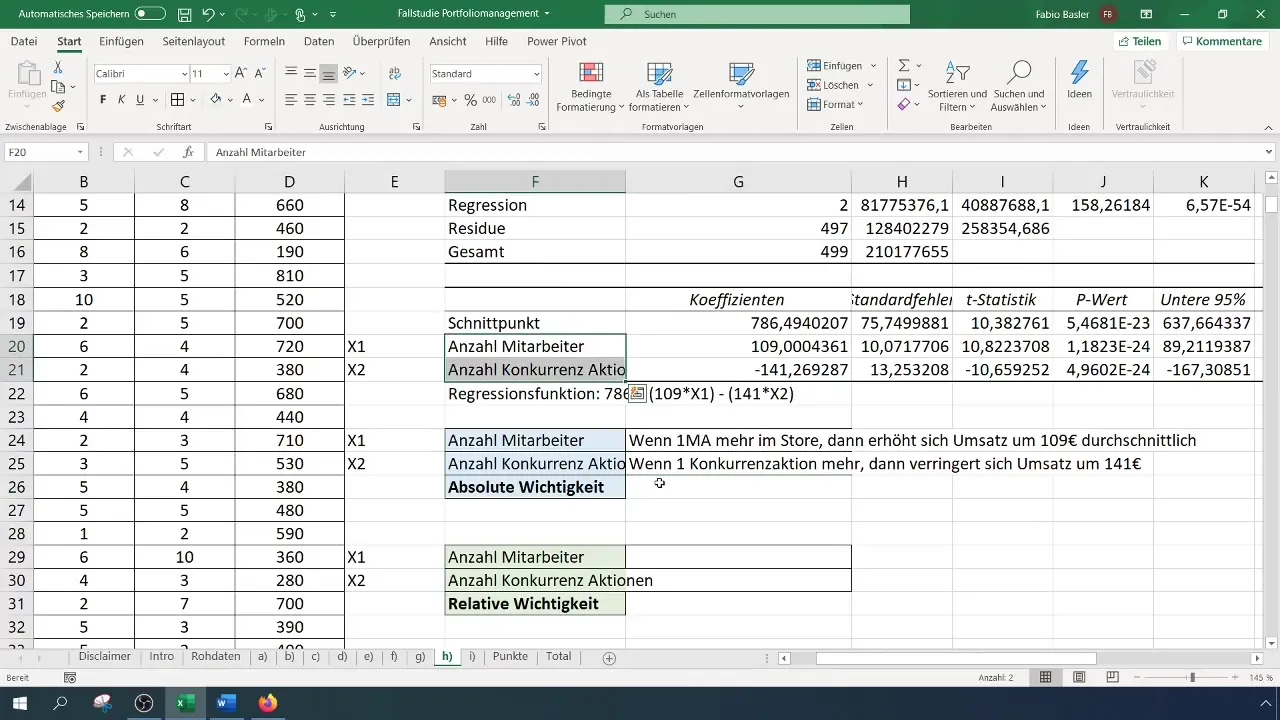
Решителна стъпка е да се определи коя от независимите променливи оказва по-силно влияние върху зависимата променлива. Това може да се направи чрез кофициентите, които показват абсолютната важност на променливите. Кофициентът на x1 (брой служители) е 109, докато кофициентът на x2 (брой конкурентни действия) е -141. Това означава, че всеки ръст на броя на служителите увеличава оборота с 109 евро, докато всеки ръст в конкурентните действия намалява оборота с 141 евро.
Оценяване на статистическата значимост
Друг важен аспект на анализа на регресията е статистическата значимост. Това може да се види от p стойностите и F-теста, които трябва да са много малки. Това показва, че независимите променливи имат значително влияние върху зависимата променлива и оправдава използването на модела.
Обобщение
Анализът на регресията в Excel ви позволява количествено да измерите връзката между различните променливи. С този наръчник научихте стъпките за изпълнение и интерпретация на множествена регресия. Внимавайте да оцените качеството и стабилността на модела, както и отделните фактори за въздействие, за да вземете обосновани решения в управлението на портфейла.
Често задавани въпроси
Кои данни са необходими за регресионния анализ?Необходима ви е зависима променлива (например оборот) и поне една или повече независими променливи (например брой служители, конкурентни действия).
Как се тълкува коэфициента на determinaciqta R²?По-висока стойност на R² означава, че по-голяма част от вариабилността в зависимата променлива се обяснява от независимите променливи.
Как може да се провери статистическата значимост?Може да използвате p-стойностите и F-теста; ниски стойности указват на висока значимост.
Каква е разликата между R² и коригирания R²?Коригираният R² взима предвид броя на независимите променливи и предлага по-реалистична оценка в модели с повече променливи.
Как може да се оцени силата на факторите на влияние?Това се постига чрез разглеждане на коефициентите на независимите променливи, които количествено определят влиянието на всяка променлива върху зависимата променлива.


