Възможността за използване на анализ на данни в Excel е от съществено значение за успешността в бизнеса и продажбите. Това ръководство се фокусира върху корелационния и регресионния анализ, за да се установи как броят на служителите и броят на телефонните обаждания влияят на оборотните данни. Изпълнението на двете анализа ви помага да оцените тези взаимоотношения количествено и прави интерпретацията на резултатите разбираема.
Най-важни заключения
- Разликата между корелация и регресия: Корелацията показва връзката между две променливи, докато регресията изучава въздействието на няколко независими променливи върху зависима променлива.
- Преглед на статистическата значимост и добротата на модела.
- Количествена оценка на важността на регресорите.
Стъпка по стъпка ръководство
1. Подготовка за анализ на данни
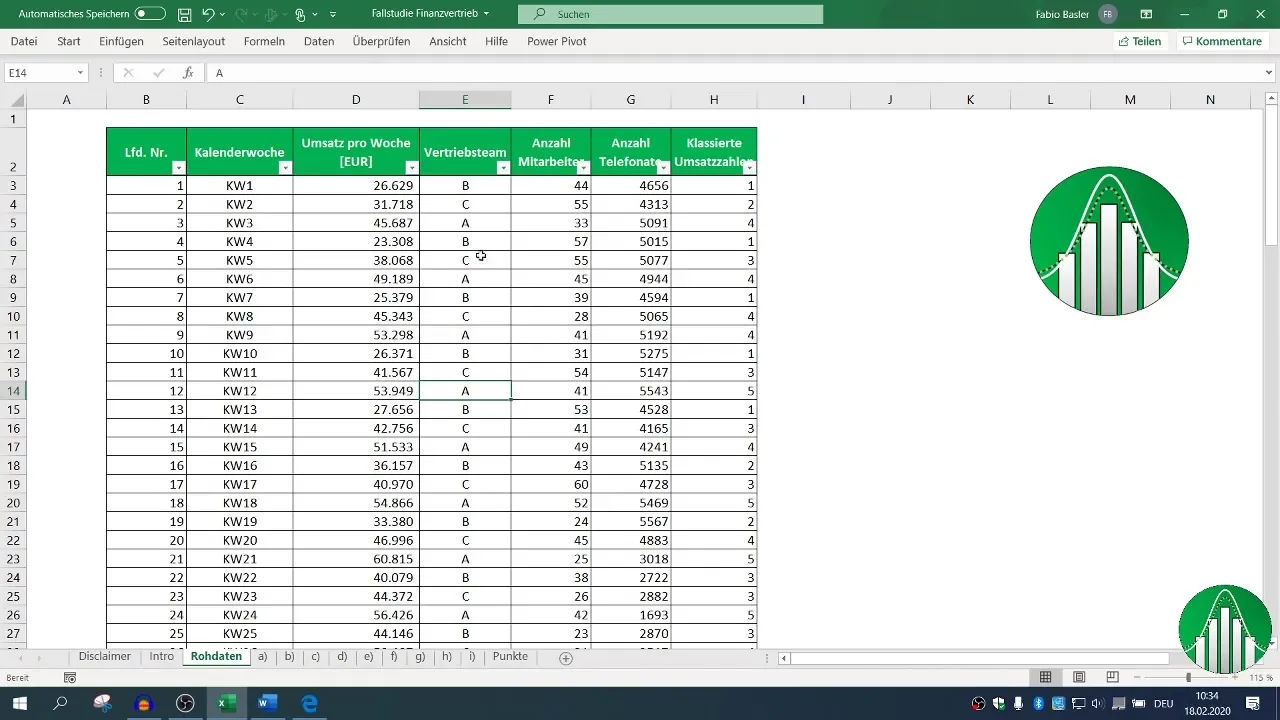
Преди да започнете анализа, уверете се, че вашите данни са правилно форматирани в Excel. Импортирайте данните за оборота, броя на служителите и телефонните обаждания в един лист на Excel. Проверете дали всички записи са пълни и необходимите променливи са налице.

2. Изпълнение на корелационния анализ
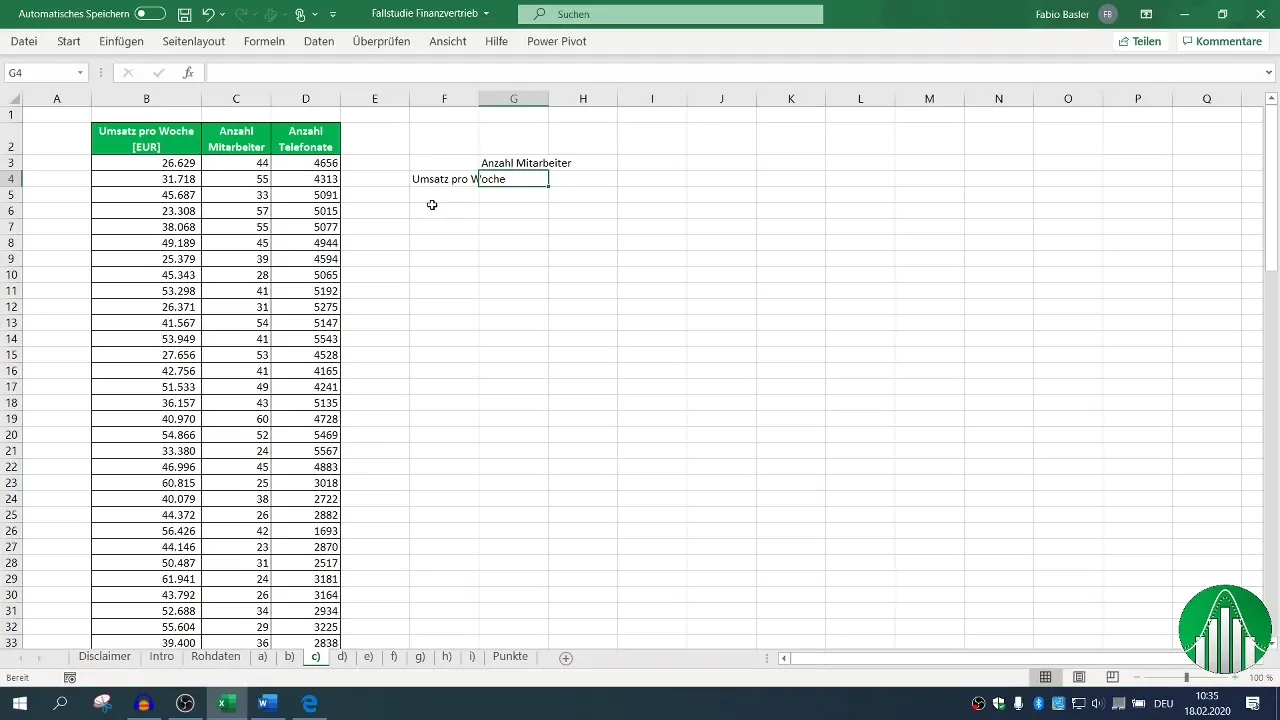
За да анализирате корелацията между оборота, служителите и телефонните обаждания, можете да пресметнете корелационния коефициент. За това използвайте формулата =КОРЕЛ() в Excel. За да получите преглед на всички променливи, създайте корелационна матрица.
Първо изберете съответните колони за оборота и броя на служителите. С формулата =КОРЕЛ( маркирайте областите за оборот и броя на служителите. Резултатът показва насколько е силна свързността.
3. Създаване на корелационна матрица
За по-подробен анализ е препоръчително да използвате функциите за анализ на данни на Excel. Активирайте функцията за анализ на данни, ако това вече не сте направили. Отидете на раздела "Данни", кликнете върху "Анализ на данни" и изберете "Корелация".
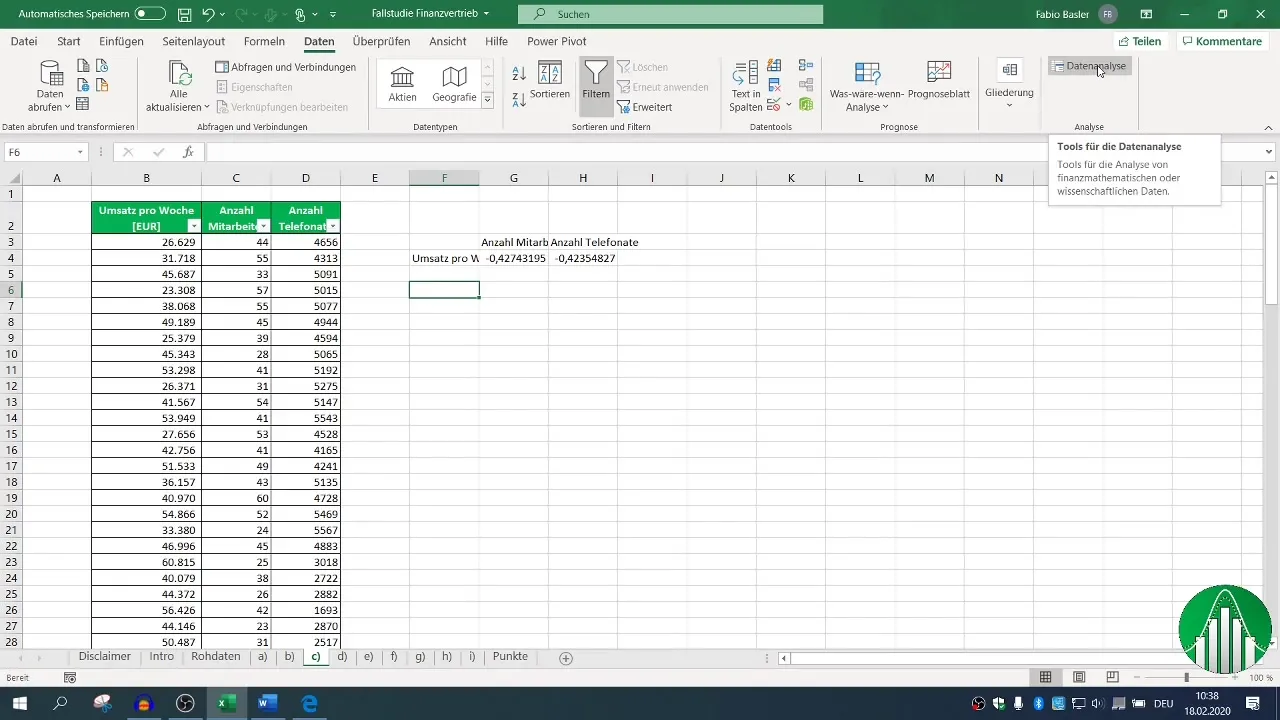
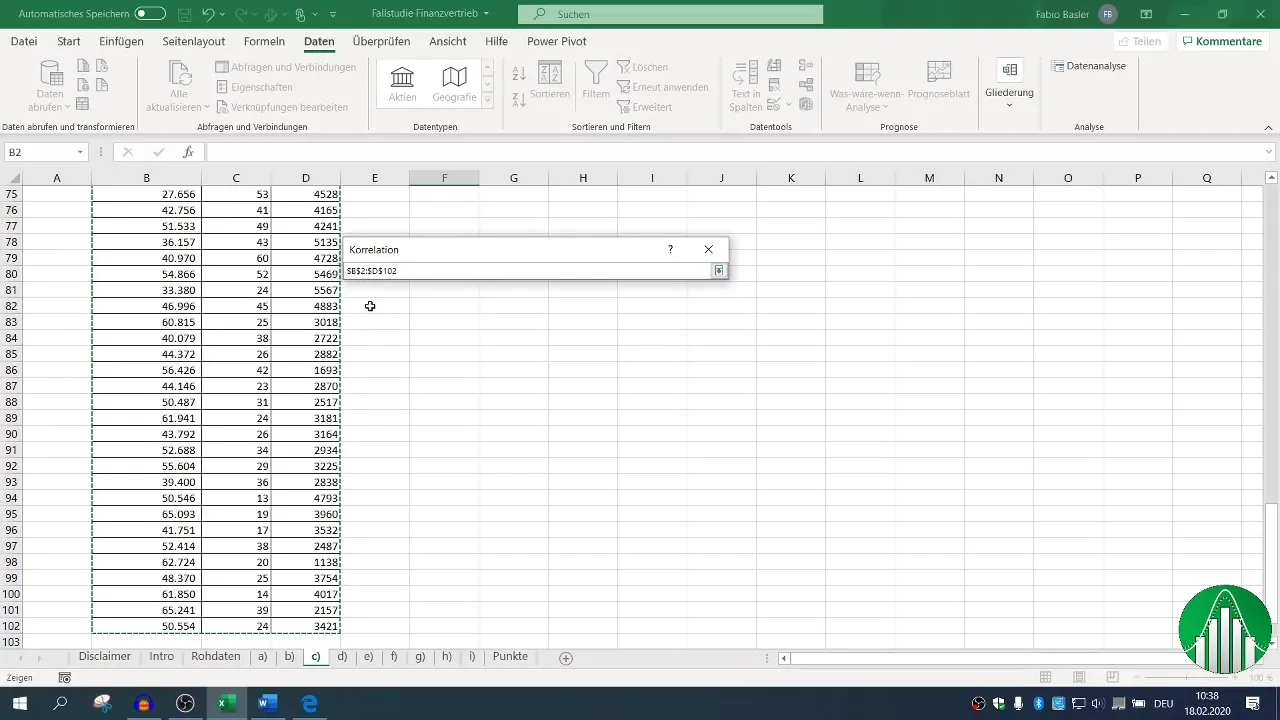
Определете входния обхват за вашите данни и поставете кръстчето за заглавията си, за да Excel разпознае правилно обозначенията. След като сте определили областта за изходните данни, можете да генерирате корелационната матрица, която показва всички съответстващи взаимоотношения.
4. Визуализация на корелациите
За да направите резултатите по-привлекателни, е възможно да е полезно да направите графично представяне чрез диаграма XY. Изберете данните си за X и Y и генерирайте облака от точки.
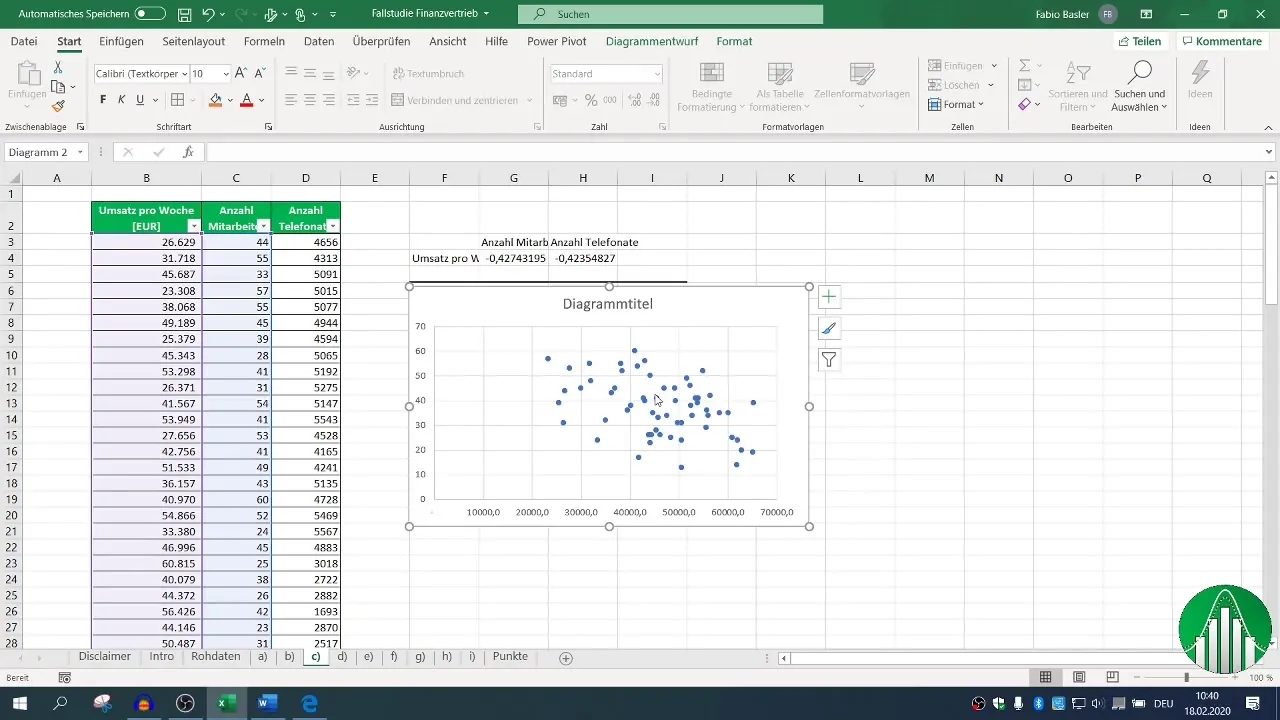
Добавете линия на тенденция, за да визуално представите връзката. Това може да предложи по-интуитивно разбиране на данните.
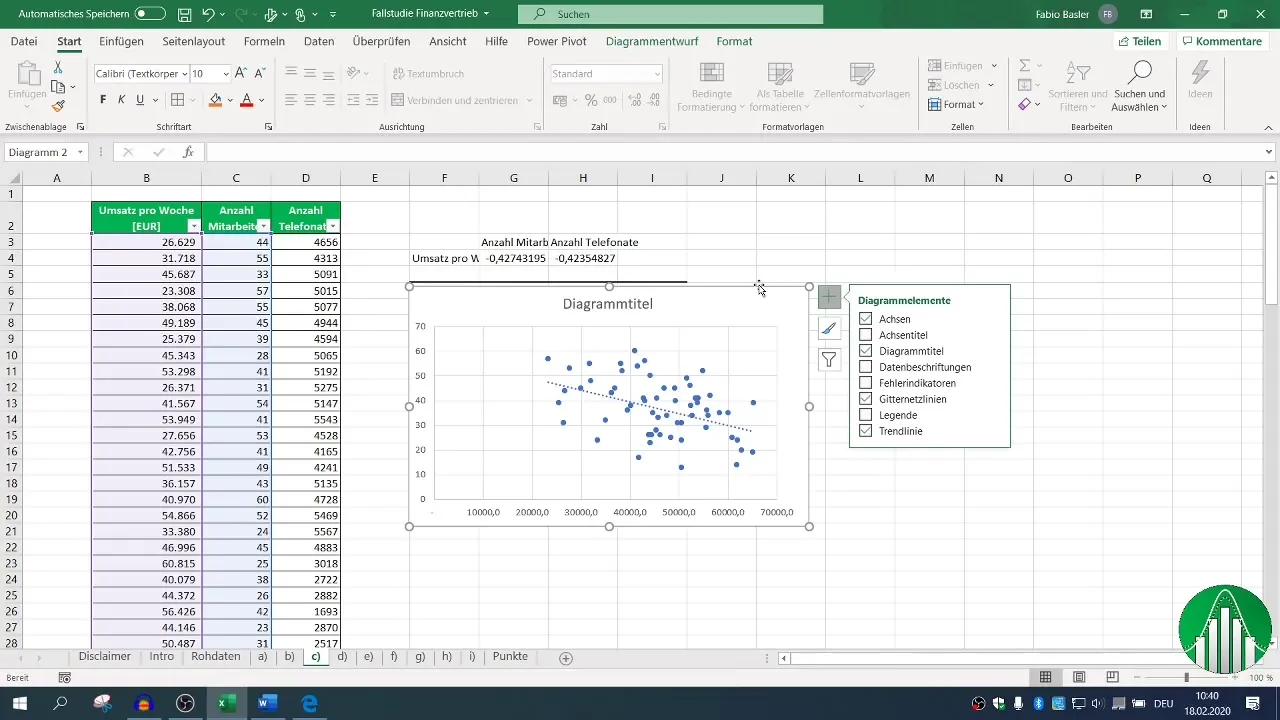
5. Изпълнение на регресионният анализ
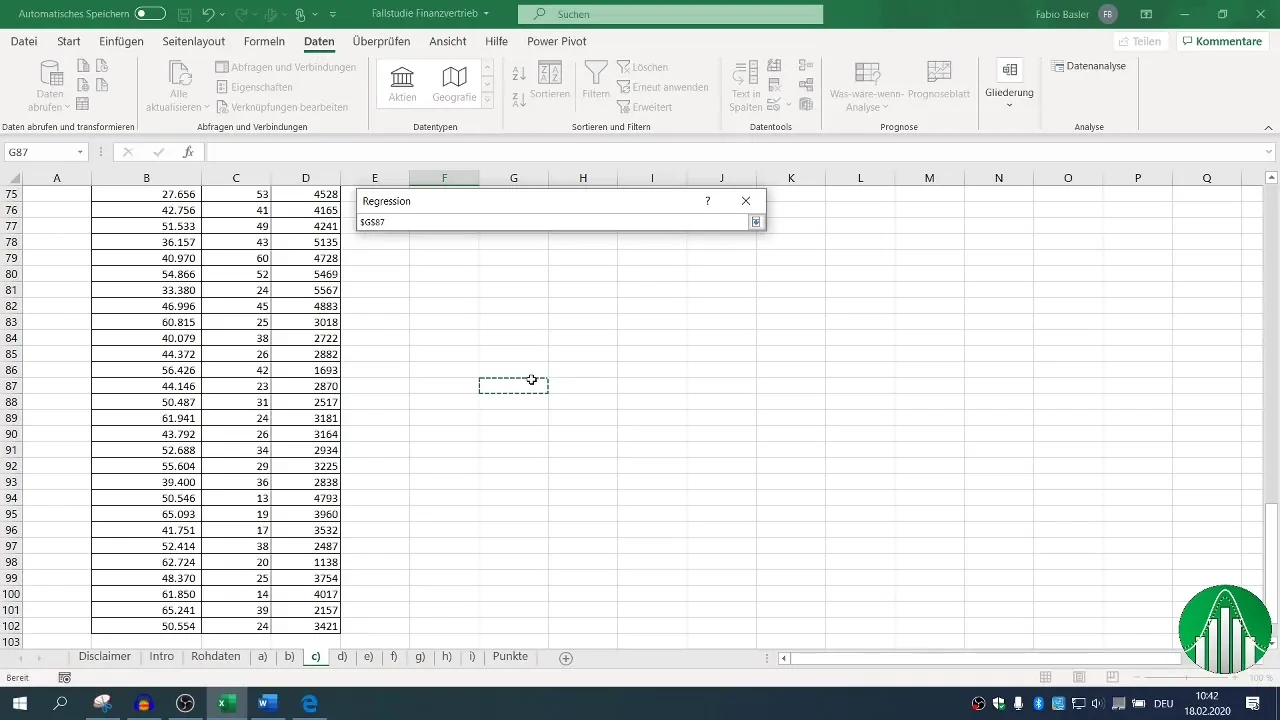
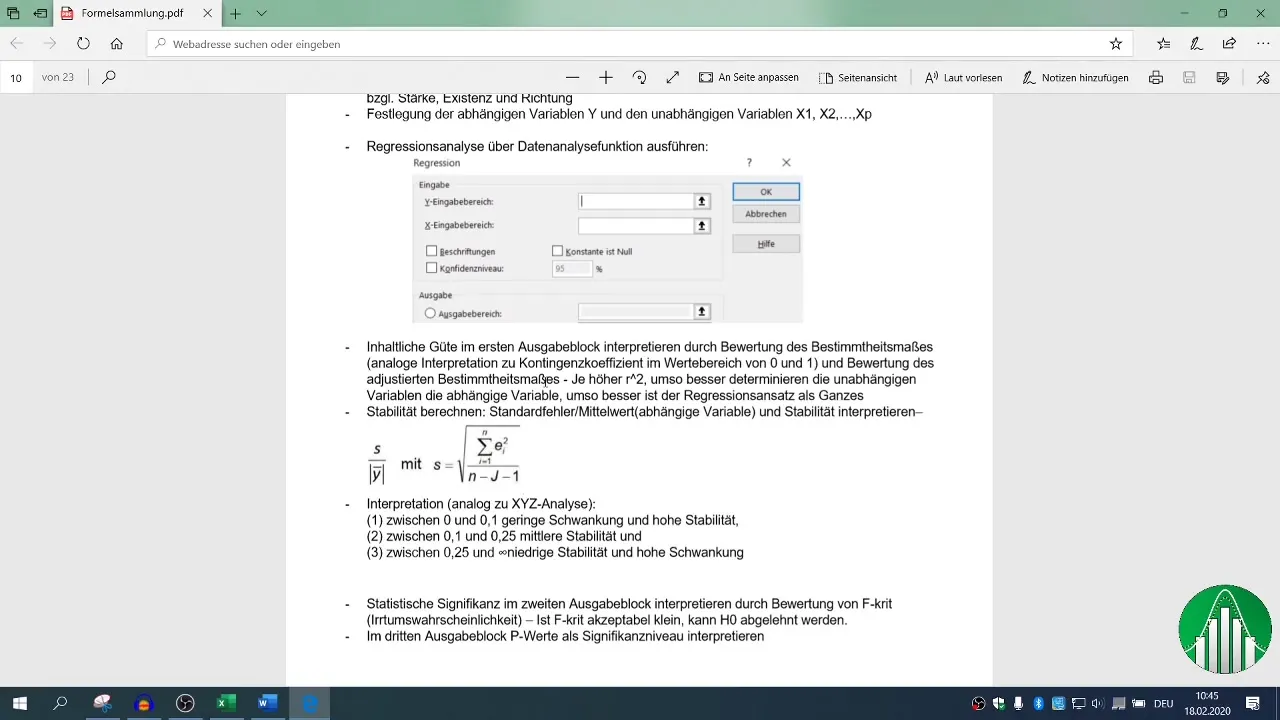
В момента следва стъпка за регресионния анализ. Отидете отново на "Данни" и изберете "Анализ на данни", след това "Регресия". Тук можете да определите за входния обхват зависимата променлива (оборот) и независимите променливи (брой на служителите и телефонните обаждания).
Уверете се, че сте задали заглавие на стойностите и дефинирайте вашия обхват на изходните данни. Стандартното ниво на доверие е зададено на 95%, което е достатъчно за повечето анализи.
6. Оценка на регресионния анализ
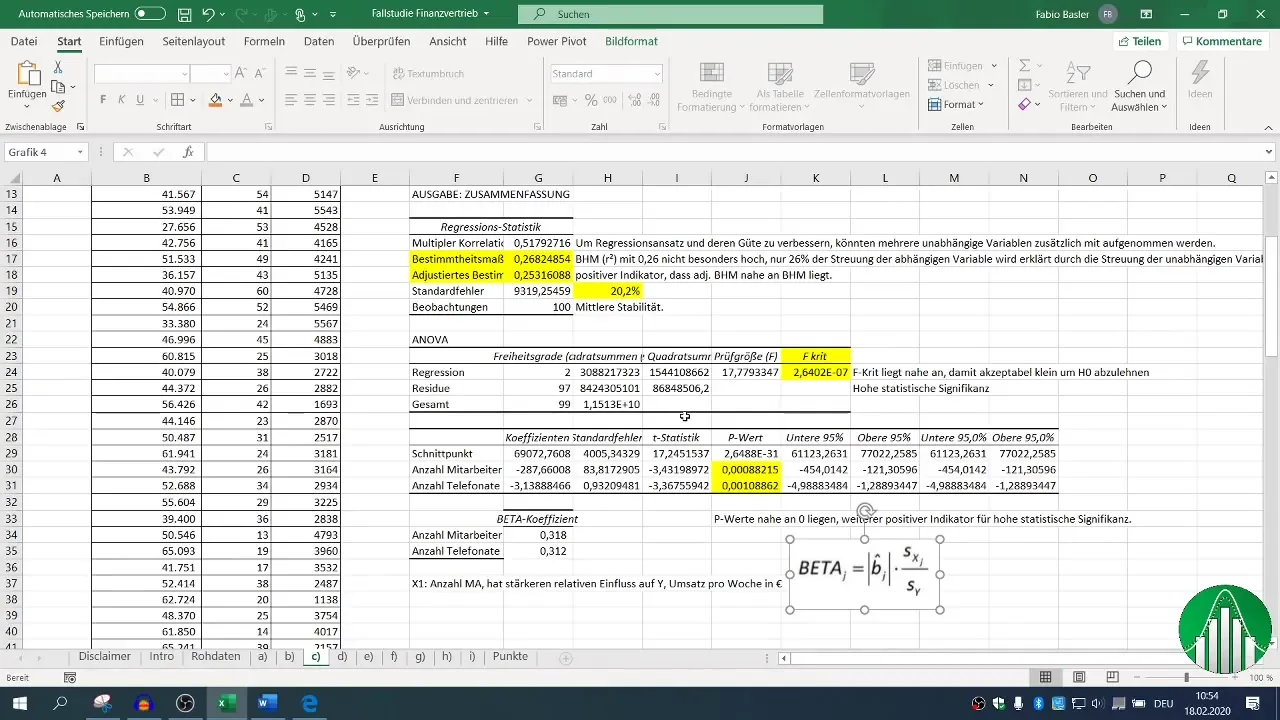
След изпълнението на регресията имате на разположение различни блокове с резултати. Съсредоточете се върху мярката за доброта (R²), която описва качеството на модела. R² от 0,26 показва, че само 26% от изменчивостта на оборотите се обясняват от независимите променливи.
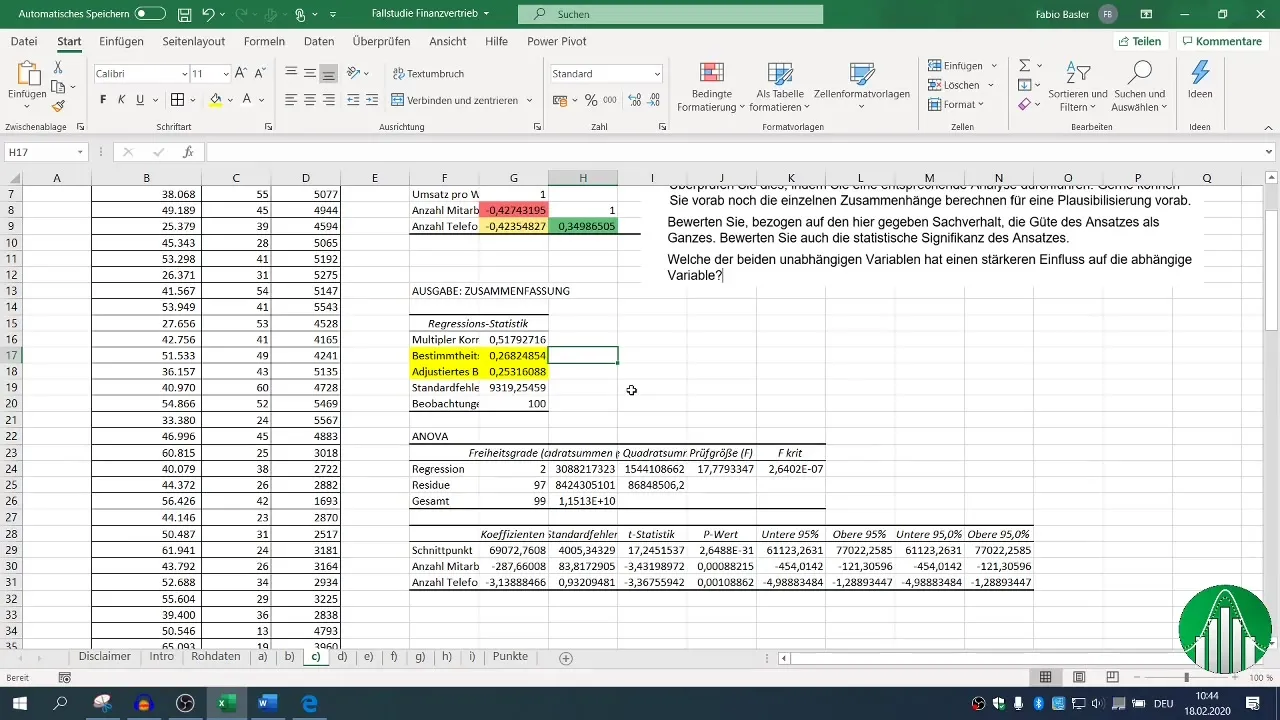
Коригираният коефициент на детерминацията трябва да бъде близо до R², което в този случай е положителен показател.
7. Оценяване на статистическата значимост
F-стойността и p-стойностите на независимите променливи са решаващи за оценката на статистическата значимост на модела ви. P-стойност под 0,05 показва, че връзката е статистически значима.
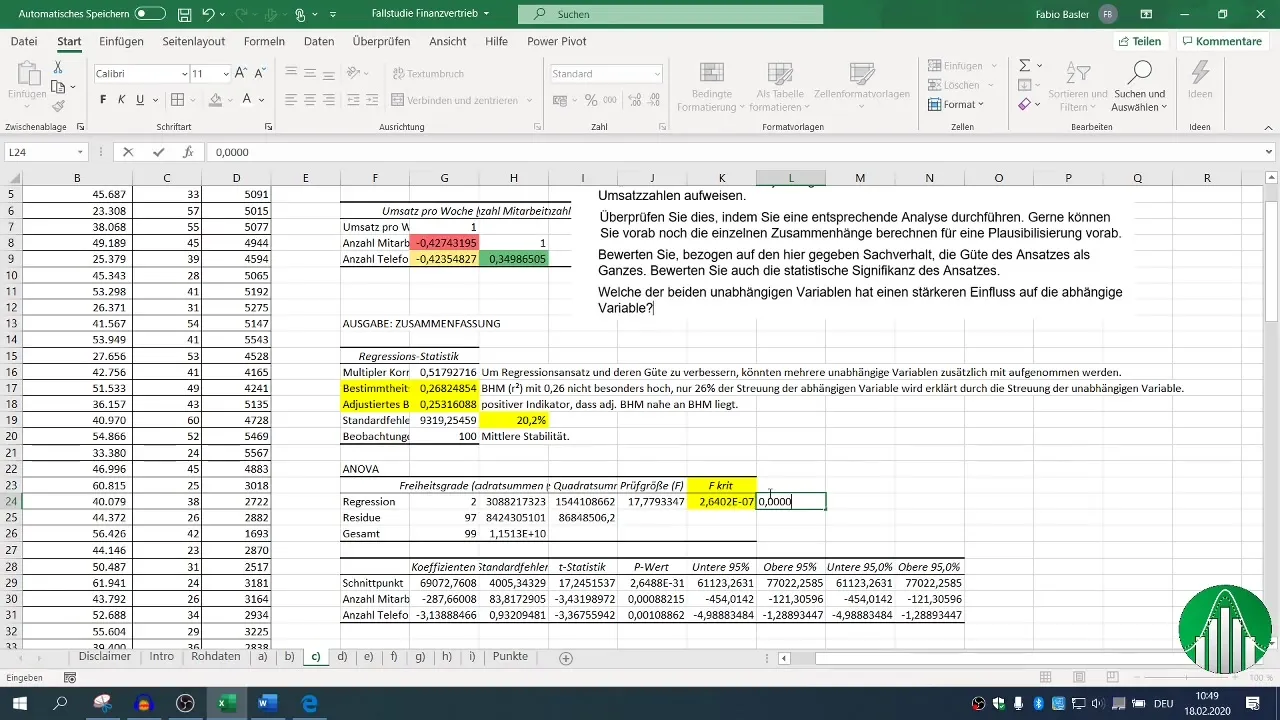
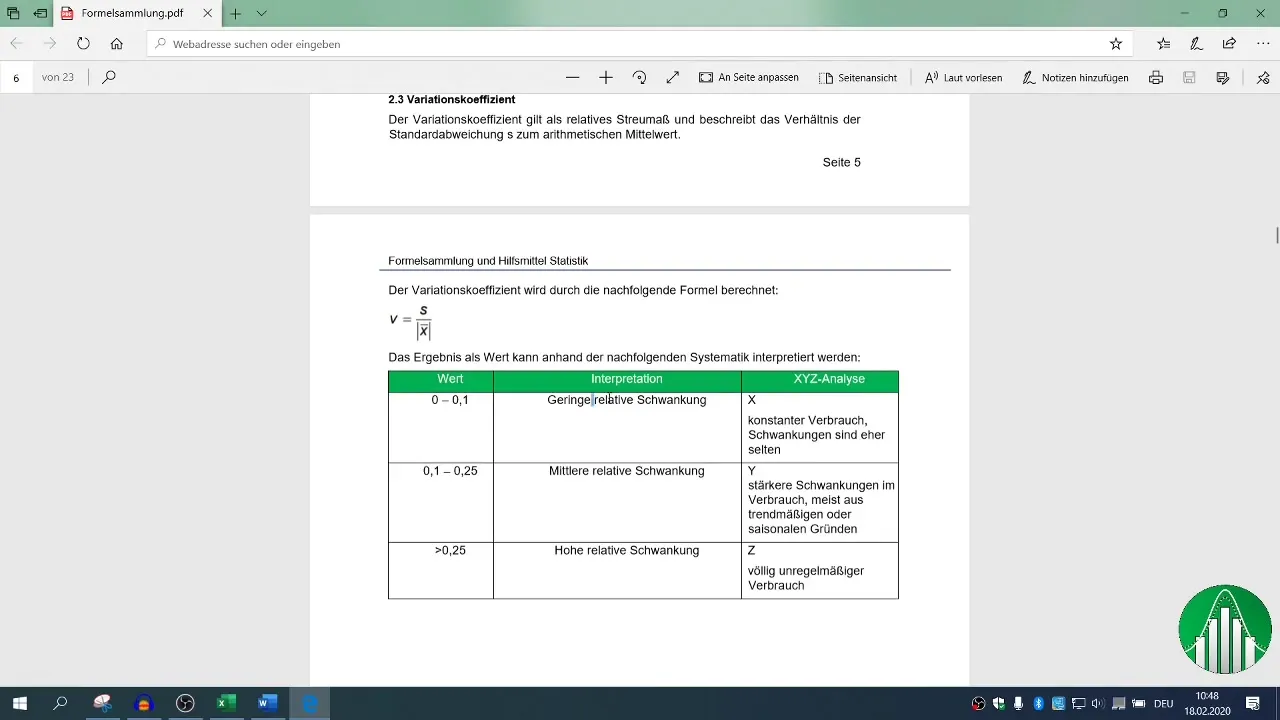
Оценяването на тези статистически показатели в контекста на R² ви помага да разберете стабилността и значимостта на резултатите си.
8. Сравнение на факторите на влияние
Накрая, интересува ви кой фактор - броят на служителите или телефонните обаждания - оказва по-силен влияние върху приходите. Тук вземате бета коефициентите и ги сравнявате.
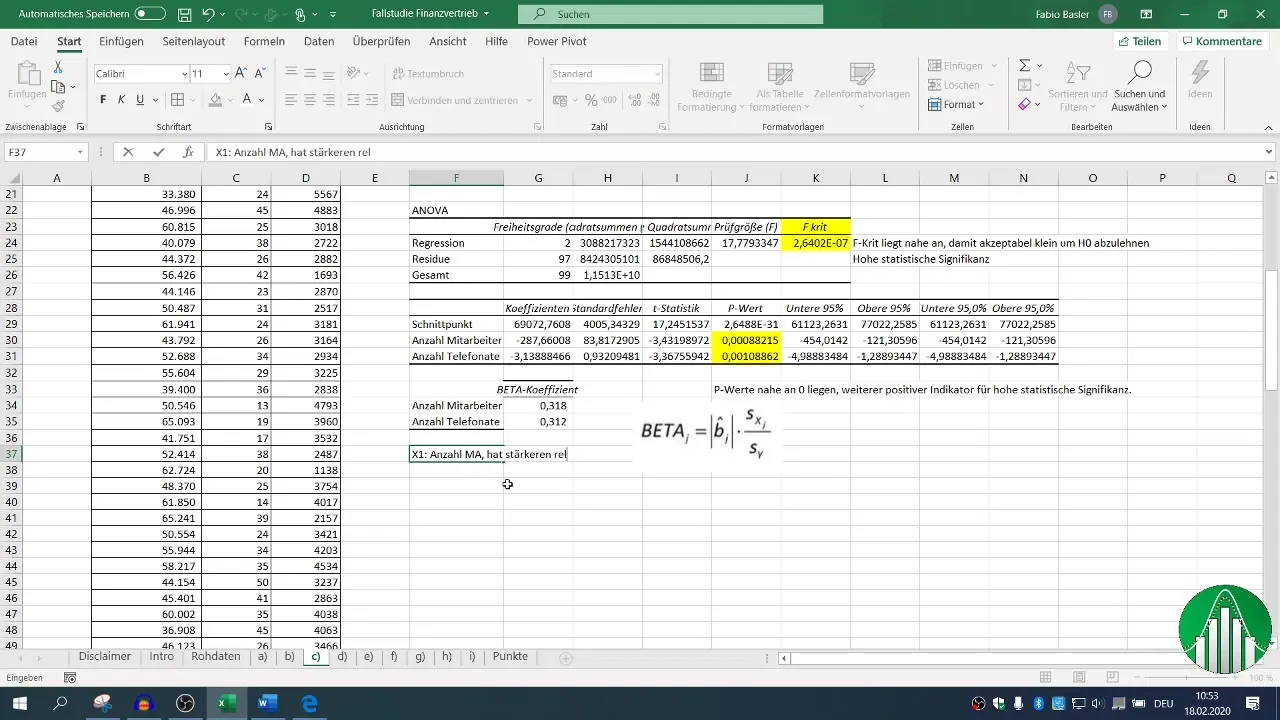
По-високият бета коефициент показва относителното влияние; може да се окаже, че броят на служителите има по-голямо влияние върху приходите отколкото броят на телефонните обаждания.
Резюме
Предходният анализ ви даде ценни насоки за статистическите връзки между променливите приход, брой служители и телефонни обаждания. Чрез систематично провеждане на корелационни и регресионни анализи в Excel можете да вземете обосновани решения, базирани на вашите резултати.
Често задавани въпроси
Защо е важен корелационният анализ?Корелационният анализ помага да се разбере връзката между две променливи, преди да се извърши подробен регресионен анализ.
Как да интерпретирам R² в регресионния анализ?R² от 0,26 означава, че 26% от вариациите в зависимата променлива (приход) се обясняват от независимите променливи.
Каква е разликата между корелация и регресия?Корелацията измерва връзката между две променливи, докато регресията оценява въздействието на няколко независими променливи върху една зависима променлива.
Как може да се тества статистическата значимост?Тествате статистическата значимост чрез p-стойността; p-стойности под 0,05 се считат за значими.
Каква е ролята на бета коефициентите?Бета коефициентите показват относителното влияние на независимите променливи върху зависимата променлива.


