Статистическите хипотезни тестове са неизбежен инструмент за предприятията, за да вземат основателни решения. В следващата секция ще ви покажем как да извършите тест на F между две извадки в Excel, за да проверите валидността на хипотезите си за вариацията в данните за оборотите си. Това ръководство ще ви насочи стъпка по стъпка през процеса, така че да можете с увереност да приложите научените техники.
Най-важните изводи
- Тестът на F между две извадки се използва за сравнение на вариациите на две групи данни.
- Целта е да се установи дали вариацията на текущите данни за обороти се различава от предположената стойност.
- Excel предоставя инструментите, необходими за извършване на необходимите изчисления и сравнения.
Ръководство стъпка по стъпка
1. Подготовка на данните
Преди да започнете теста, уверете се, че вашите данни са подготвени. Важно е да премахнете филтрите, за да включите всички съответни данни. Започнете като изберете данните в съответните колони.

2. Задаване на параметрите
Задайте параметрите за вашия тест. Трябва да знаете колко данни точки анализирате. В нашия пример предполагаме, че разполагате с 100 цифри за оборот, които са с нормално разпределение.

3. Запис на предходната стойност на вариацията
Известната стойност на вариацията или оборота от миналото играе централна роля във вашата анализа. В този пример предишната стойност е 116 милиона евро на седмица.
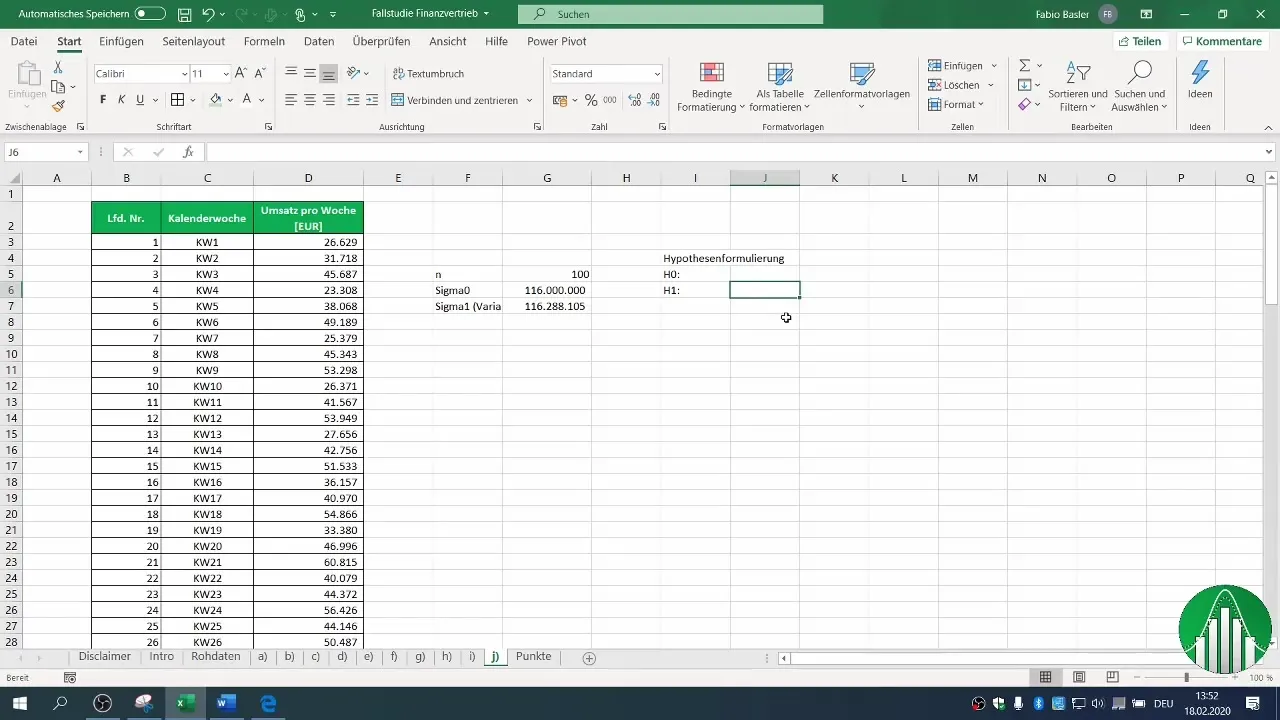
4. Формулиране на хипотезите
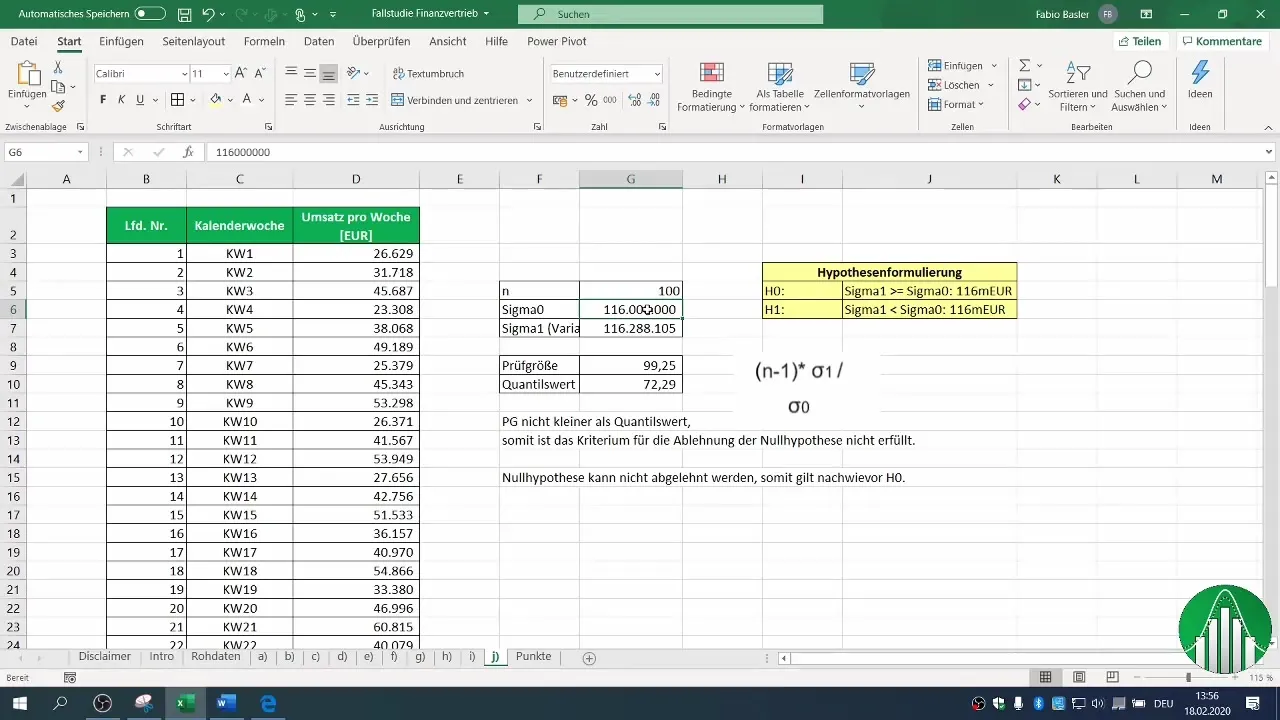
Формулирайте вашата нулева хипотеза (H0) и алтернативна хипотеза (H1). В този случай H0 е, че вариацията е равна на или по-голяма от 116 милиона, докато H1 предполага, че вариацията се е намалила.
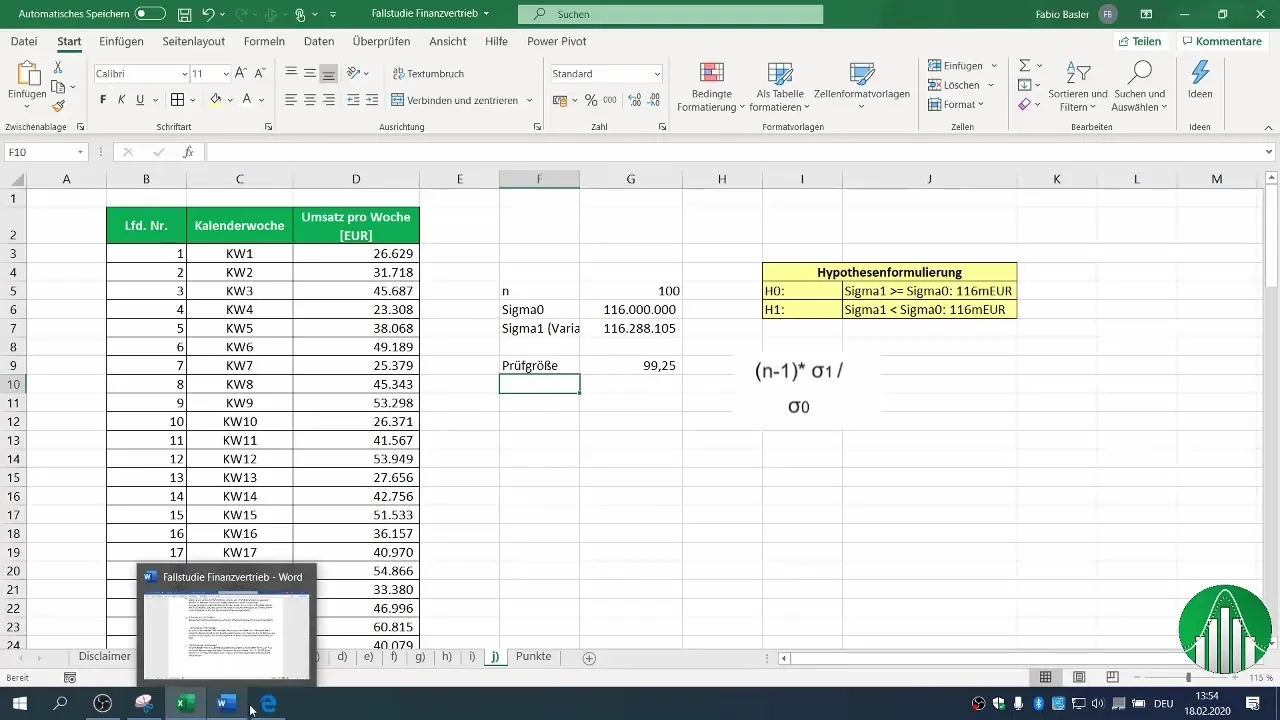
5. Изчисляване на тестовата стойност
Тестовата стойност може да се изчисли посредством вариацията на вашия пробен образ. Извършете необходимите изчисления, за да определите стойността за вашата тестова стойност. Тя се изчислява чрез формулата: (n-1) * σ1 / σ0, където σ1 е вариацията на вашата проба, а σ0 е вариацията от миналото.
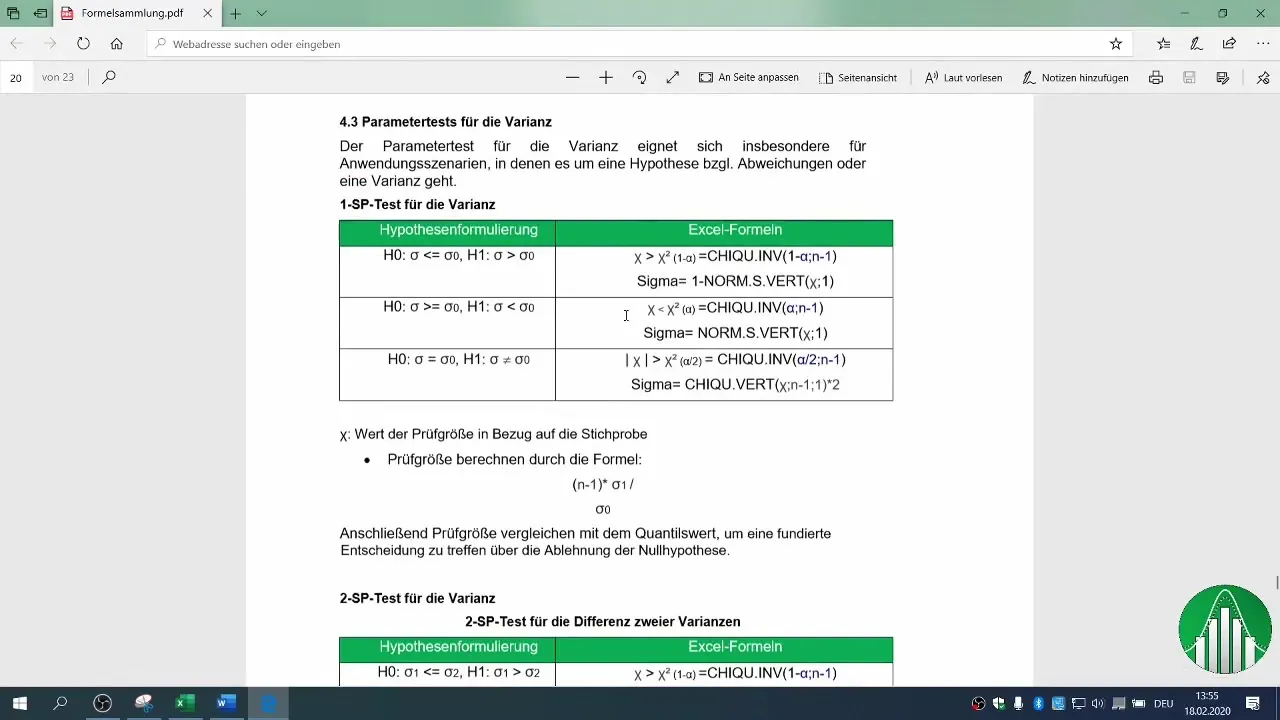
6. Определяне на критичния регион
За да решите дали можете да отхвърлите нулевата хипотеза, трябва да зададете критичния регион. Използвайте таблицата на разпределението на Хи-квадрат за вашия ниво на увереност. В нашия пример използвахме вероятността за грешка от 2%.
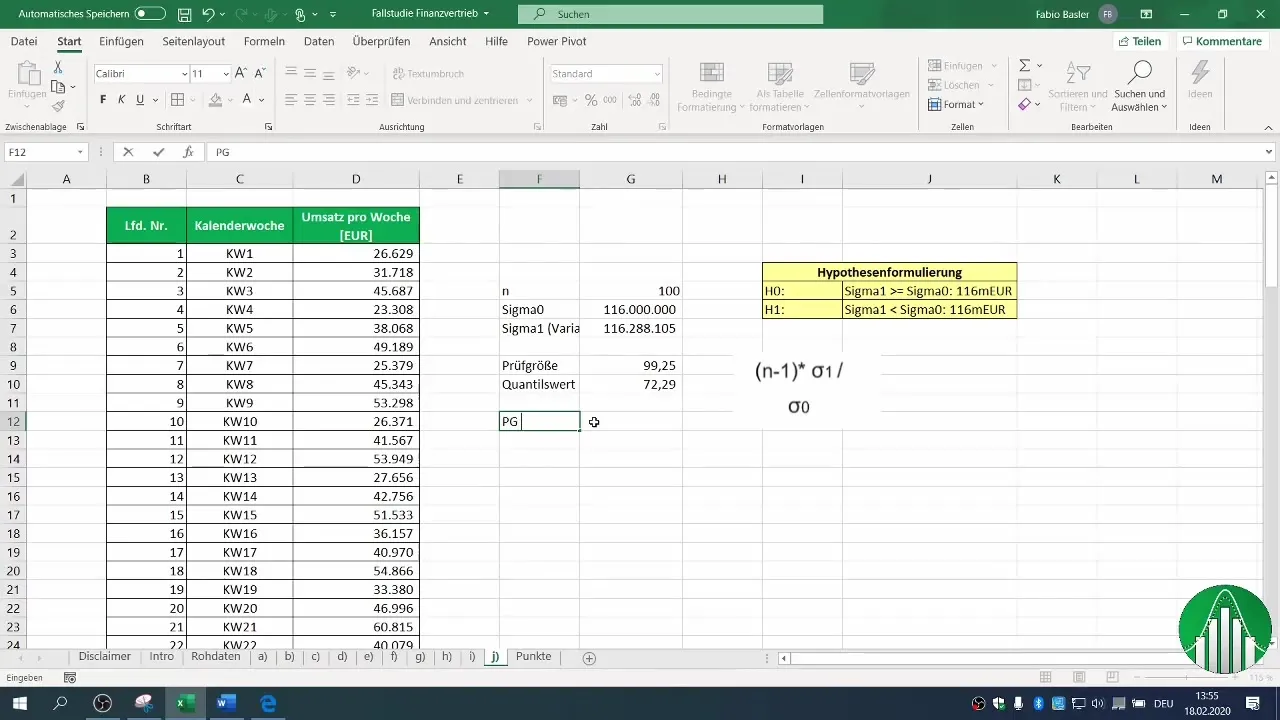
7. Сравняване на тестовата и критичната стойност
Сега проверете дали изчислената ви тестова стойност е по-малка от критичната стойност. В този случай установихме, че нашата тестова стойност не е по-малка от критичната стойност на квантила.
8. Изводи
Като базирате сравнението си, вие вече можете да решите дали да отхвърлите или не нулевата хипотеза. В нашия пример установихме, че нулевата хипотеза не може да бъде отхвърлена. Това указва, че вариацията на вашите данни за обороти остава на приетата стойност или дори е по-голяма.
Резюме
В това ръководство подробно разгледахме как да извършите тест на F между две извадки в Excel. Научихте как да подготвите данните си, да формулирате хипотези, да изчислите тестовата стойност, да зададете критичния регион и накрая да направите вашите изводи. С тези стъпки сте добре подготвени да извършвате статистически анализи самостоятелно.
Често задавани въпроси
Какво е тестът на F между две извадки?Тестът на F между две извадки се използва за сравнение на вариациите на две групи данни.
Как формулирам хипотези за теста на F?Нулевата хипотеза утвърждава, че вариацията е равна или по-голяма, докато алтернативната хипотеза предполага намаляване.
Как да намеря критичната стойност за теста си?Критичната стойност може да бъде извлечена чрез таблици на Хи-квадрат, базирано на нивото на увереност и степените на свобода.
Какво да направя, ако не мога да отхвърля нулевата хипотеза?Това означава, че данните съответстват на приетата стойност за вариацията или дори показват по-високи колебания.
Имам нужда от специален софтуер за теста?Excel е достатъчен за извършване на тест на F между две извадки, докато данните са подготвени.

