Google Sheets: Statistické funkce pro analýzu dat

V dnešním tutoriálu se budeme zabývat statistickými funkcemi v Google Sheets. Statistické funkce hrají důležitou roli při analýze dat, zejména pokud pracujete s větším množstvím dat. V tomto kontextu se naučíme, jak vypočítat průměry, měřítka rozptylu a vztahy mezi daty. Tento průvodce tě provede klíčovými funkcemi a pomůže ti vybudovat základní porozumění deskriptivní statistice.

Nejdůležitější poznatky

• Naučíš se, jak spočítat aritmetický průměr, modus a medián v Google Sheets.
• Získáš vhledy do výpočtu kvantilů, směrodatných odchylek a rozptylů.
• Odhalíš, jak analyzovat statistické vztažnosti mezi různými datovými sadami.

Krok za krokem

Úvod do statistických funkcí

Nejprve si podrobně prozkoumáme různé statistické funkce v Google Sheets. V Google Sheets můžeš kliknout na kartu "Funkce" a zobrazit řadu kategorií, včetně statistických funkcí. Tyto funkce jsou klíčové, pokud pracuješ s rozsáhlými datovými sadami a chceš rychle a efektivně získat poznatky.

Výpočet průměru

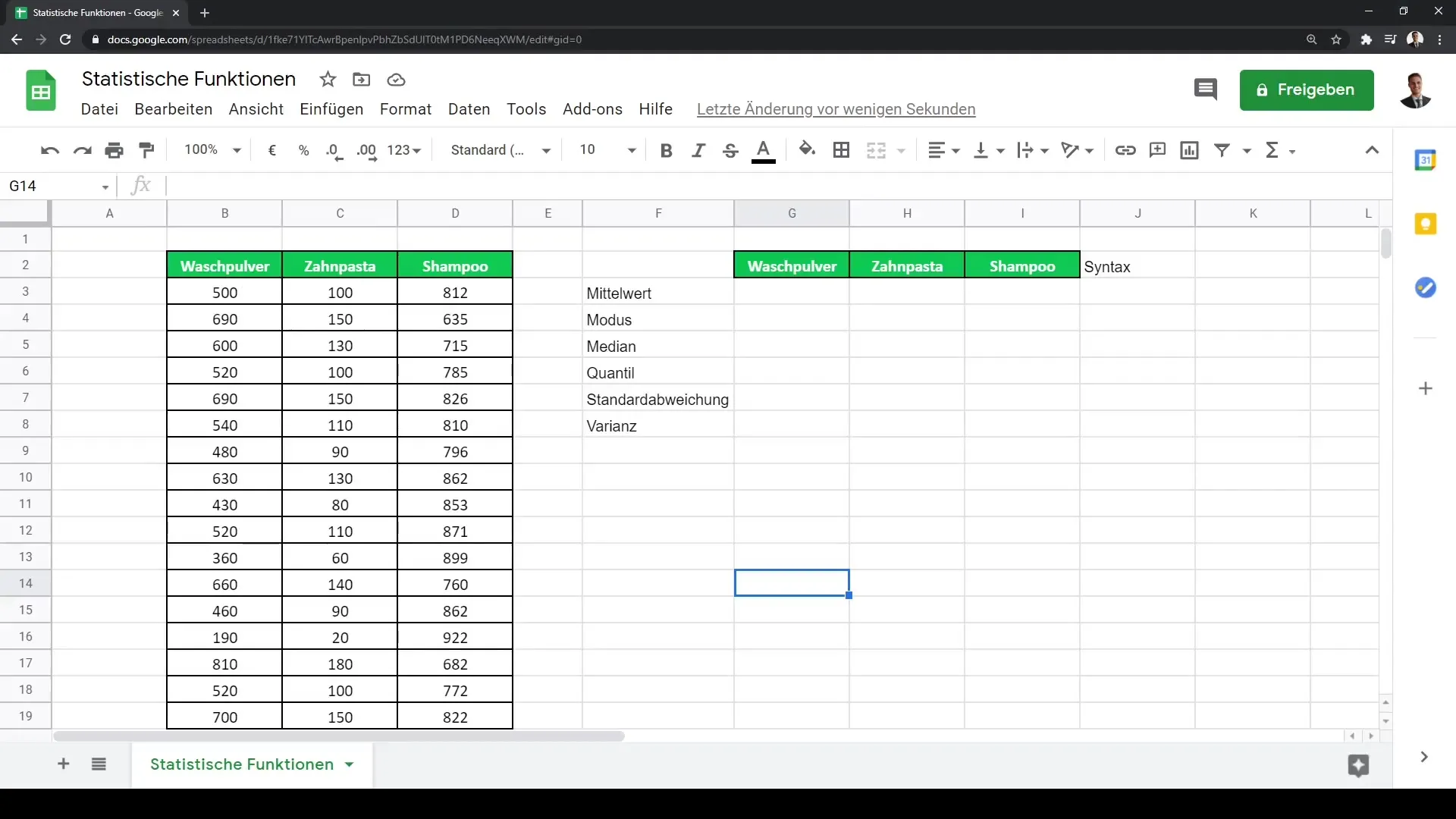
Začněme s takzvanými ukazateli průměru. Aritmetický průměr, též nazývaný průměr, patří mezi základní ukazatele v statistice. Pro výpočet průměru můžeš použít vzorec PRŮMĚR. Představme si, že jsi podnik zaměřený na spotřební zboží a chceš spočítat průměrný obrat z různých produktových oblastí, jako jsou prací prášek, zubní pasta a šampon.

K tomu můžeš použít vzorec =PRŮMĚR(B2:B4), kde B2 až B4 jsou buňky obsahující tvé údaje o obratu.

Modus a medián

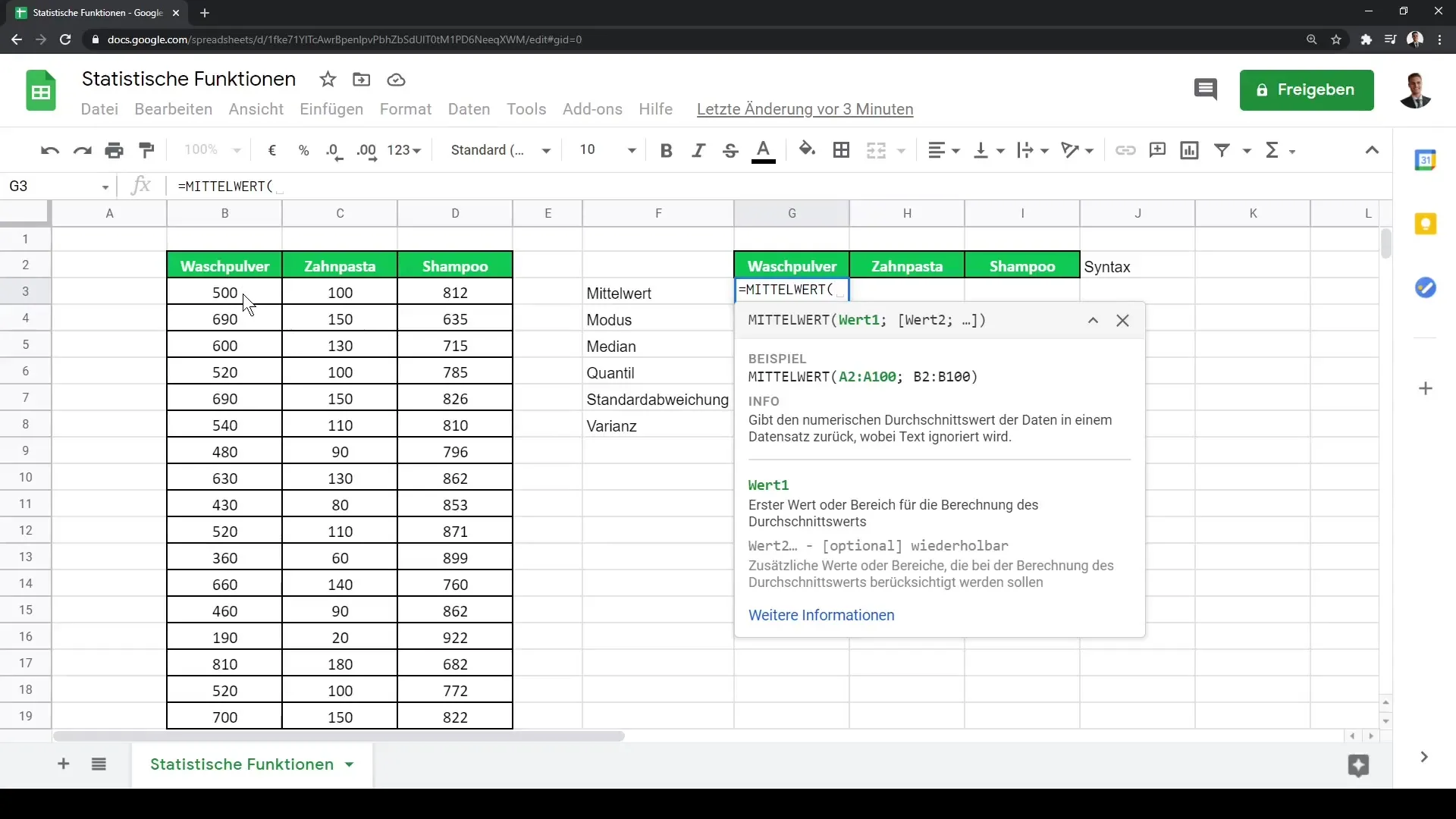
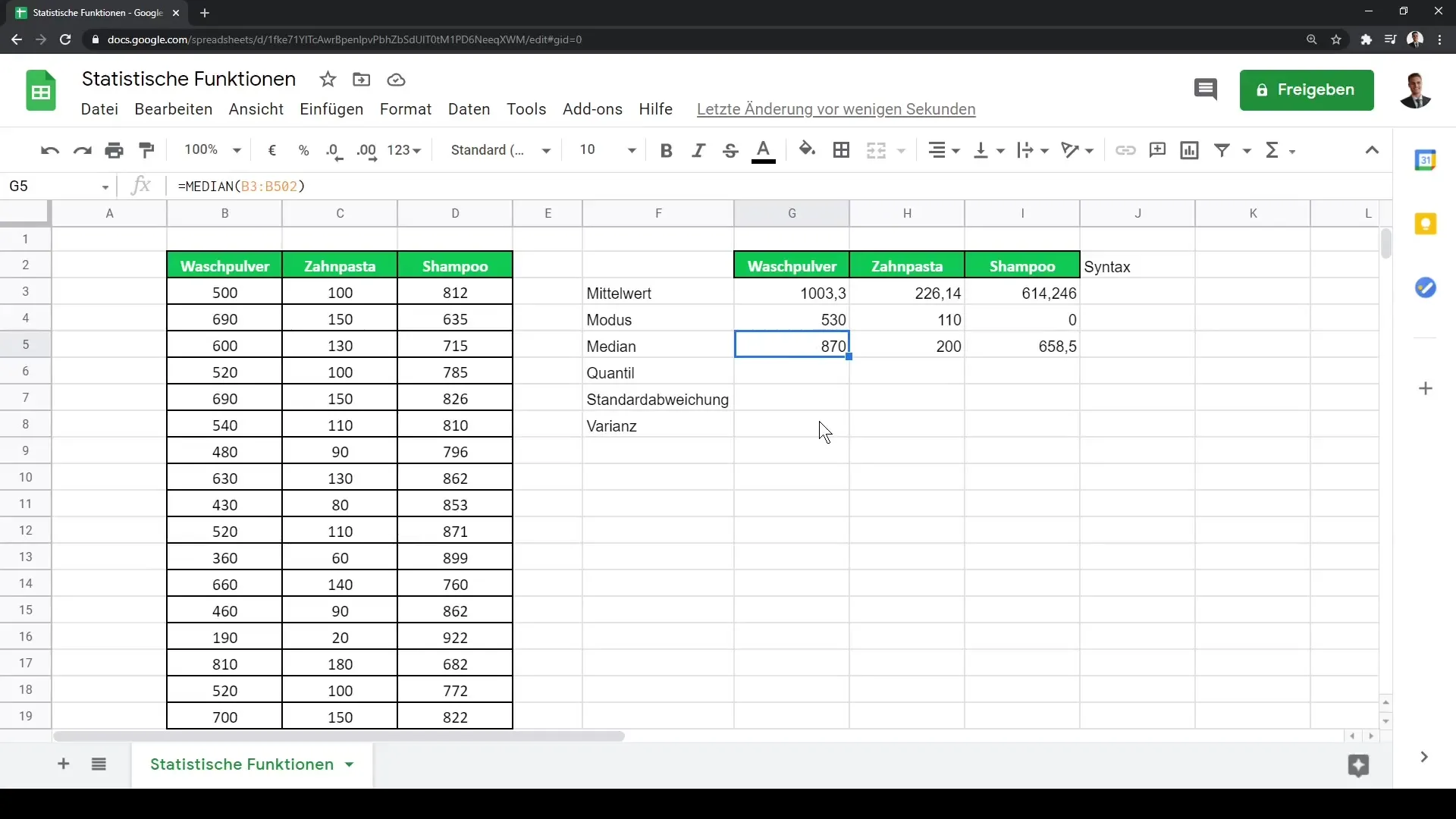
Dalším důležitým ukazatelem je modus, který určuje nejčastější hodnotu v datové sadě. Toho můžeš dosáhnout vzorcem MODUS, který dokáže pracovat i s texty. Například můžeš určit obrat různých produktů tím, že vyfiltruješ nejčastější obraty.

Medián ti ukáže hodnotu, která leží přesně uprostřed tvých dat, když jsou seřazena vzestupně. Pro výpočet mediánu můžeš použít vzorec MEDIÁN, např. =MEDIÁN(B2:B4).

Výpočet kvantilů

Kvantily ti pomáhají lépe porozumět distribuci tvých dat. Můžeš spočítat první (0,25) a třetí (0,75) kvartil pomocí vzorce KVARTIL. To ti poskytne cenné poznatky o distribuci tvých dat. Například můžeš použít =KVARTIL(B2:B4, 1) pro první kvartil.

Analýza rozptylu

Směrodatná odchylka je důležitým ukazatelem rozptylu tvých dat. Můžeš spočítat směrodatnou odchylku pomocí vzorců STØDEVAP nebo STØDEV. Směrodatná odchylka ti pomůže pochopit, jak silně se data kolem průměru rozptylují. Například bys mohl použít =STØDEV(B2:B4) k výpočtu směrodatné odchylky tvých obratů.

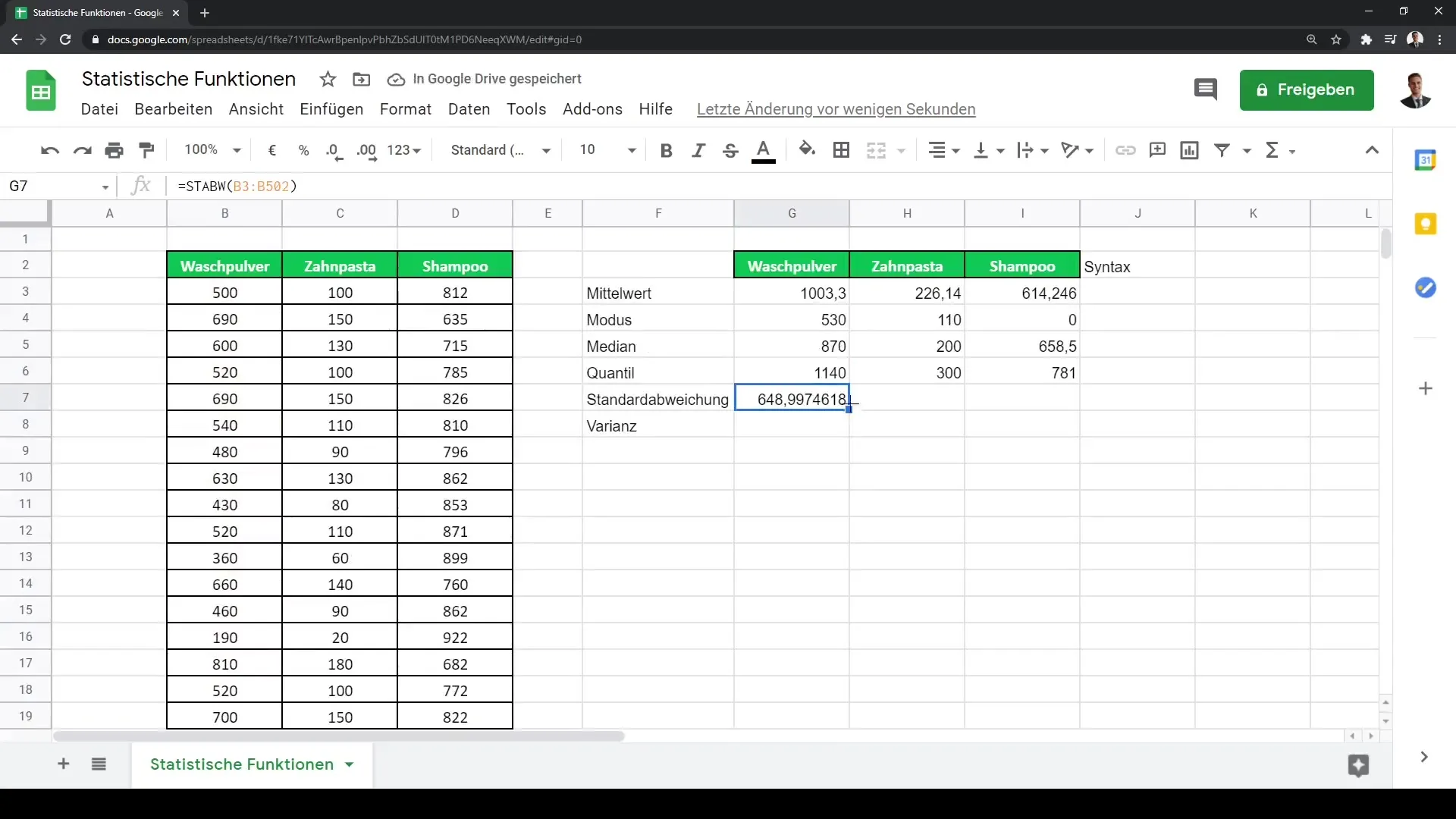
Pro výpočet rozptylu můžeš použít vzorec VAR.P, který poskytuje rozptyl populace tím, že umocníš směrodatnou odchylku. To ti pomůže získat nejen kvantitativní hodnotu pro rozptyl, ale i odkaz na další statistické analytické postupy.

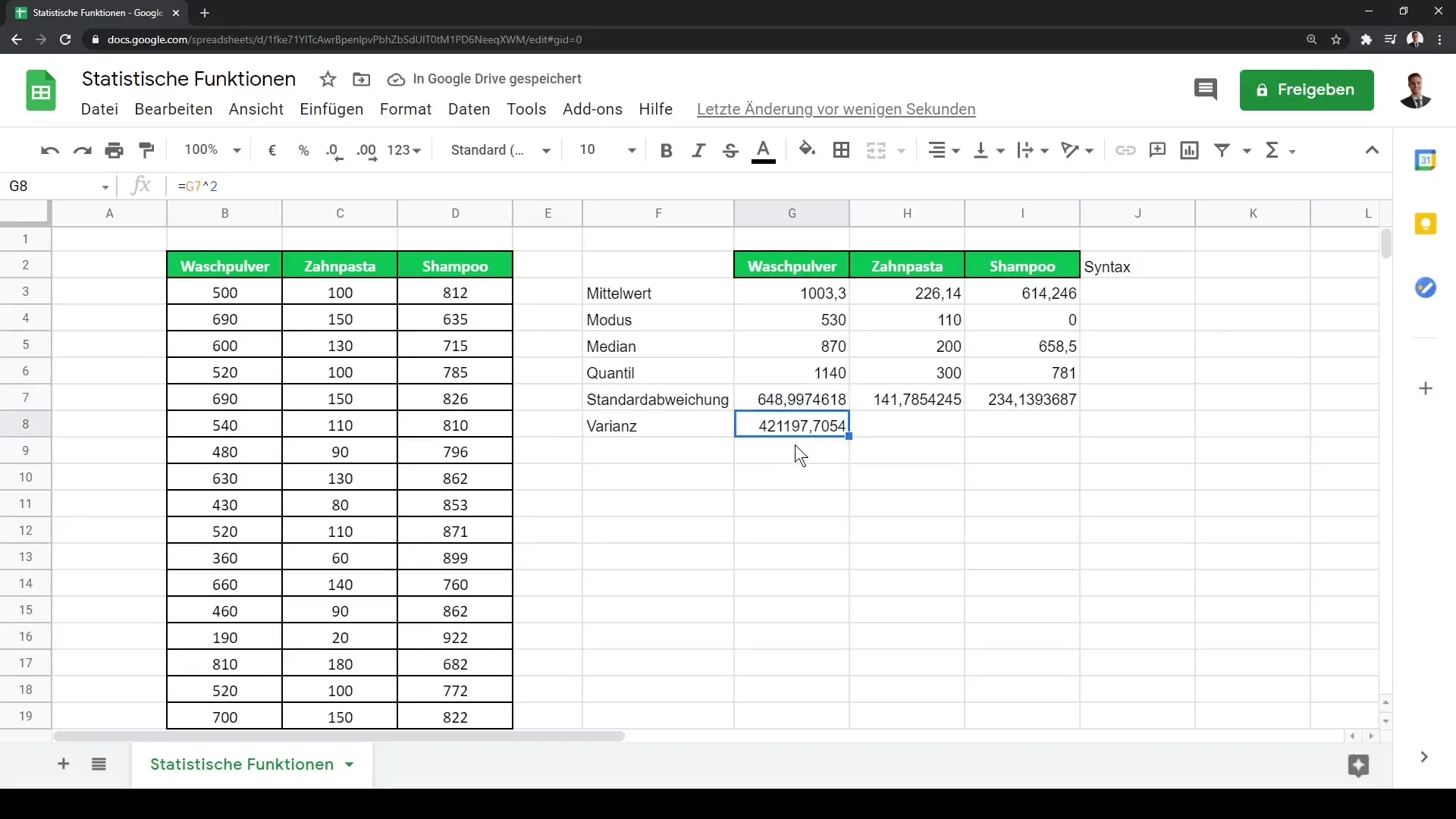
Vztahy mezi datovými sadami

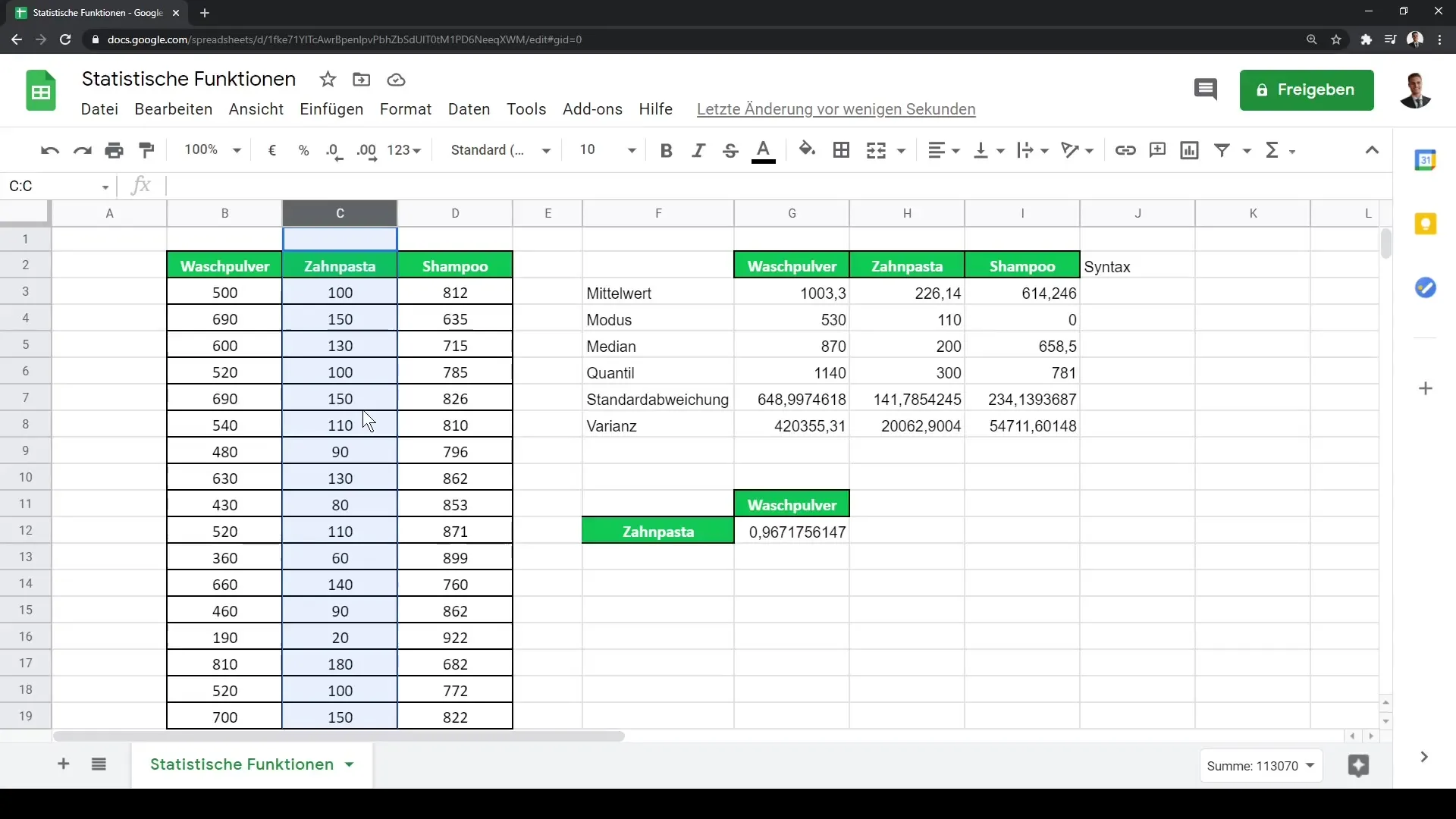
Po výpočtu polohy a rozptylu tvých dat je také důležité zjistit, zda existuje vztah mezi různými datovými sadami. Jedním z příkladů může být zkoumání vztahu mezi obraty pracího prášku a zubní pasty. Můžeš spočítat Pearsonův korelační koeficient pomocí vzorce CORREL, abys ověřil, zda existuje statistický vztah.

Například bys použil =CORREL(A2:A4, B2:B4), kde A2 až A4 představují obraty pracího prášku a B2 až B4 obraty zubní pasty. Hodnota blízko 1 ukazuje silný pozitivní vztah, zatímco hodnota blízko -1 ukazuje silný negativní vztah.

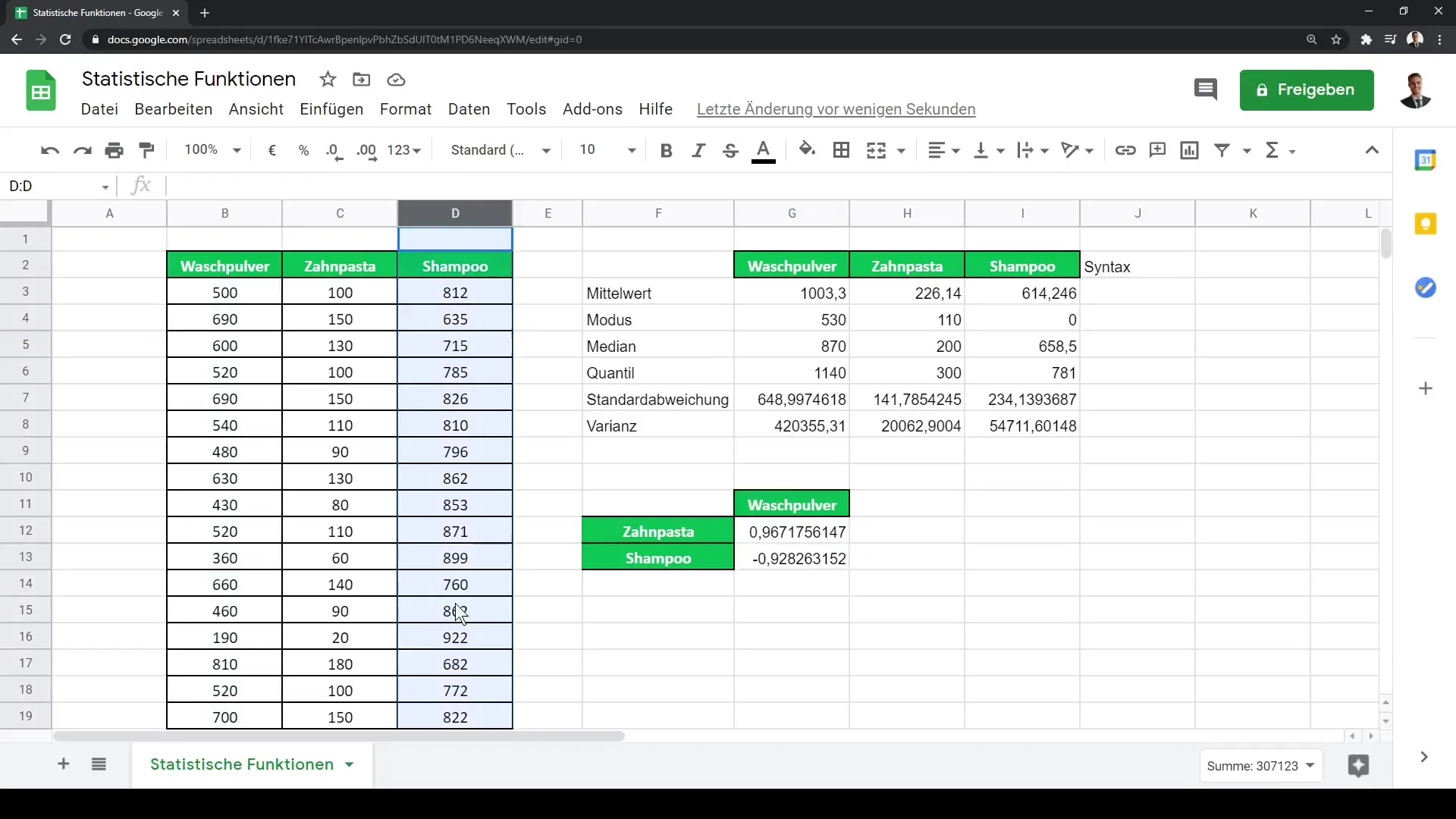
Pokud chcete analyzovat další vztahy, například mezi pracím práškem a šamponem, můžete postupovat podobně a zkoumat korelaci mezi těmito kategoriemi produktů.

Shrnutí

V tomto tutoriálu jste se seznámili s různými statistickými funkcemi v Google Sheets. Výpočet průměru, modu, mediánu a kvantilů, stejně jako analýza měr rozptylu jako je směrodatná odchylka a rozptyl, jsou důležité pro každou statistickou analýzu. Navíc jste se seznámili s průzkumem souvislosti mezi různými datovými sadami, které vám pomáhají získat hlubší pochopení vašich dat.