Test Chi-kvadrát úpravy je jednoduchou metodou k ověření hypotézy, zda daná řada dat sleduje normální rozdělení. V této příručce se naučíte, jak provést test Chi-kvadrát v Excelu k zjištění, zda obraty ze smartphonů odpovídají normálnímu rozdělení. Půjdeme krok za krokem procesem od vytvoření třídicí tabulky četností až po výpočet testovací velikosti a její srovnání s kritickou hodnotou Chi-kvadrátu.
Nejdůležitější poznatky
- Test Chi-kvadrát úpravy pomáhá při testování normálních rozdělení.
- Je důležité vytvořit třídicí tabulku četností.
- Testovací velikost se porovnává s kritickou hodnotou, abychom buď zamítli nebo přijali nulovou hypotézu.
Krok za krokem návod
Krok 1: Příprava dat
Pro provedení testu Chi-kvadrát musíte nejprve mít data. Zkopírujte obraty ze smartphonů do listu programu Excel. Ujistěte se, že jsou vaše data uspořádána v jednom sloupci.

Krok 2: Vytvoření histogramu
Pro získání prvních vizuálních náznaků rozložení vytvořte histogram vašich dat. Chcete-li to provést, přejděte na "Vložit" a vyberte "Grafy". Přidejte histogram tím, že vyberete rozsah dat.
Krok 3: Vytvoření třídicí tabulky četností
Pro test Chi-kvadrátu potřebujete třídicí tabulku četností. Nejprve stanovte počet tříd pro vaši tabulku – v tomto případě používáme šest tříd. Vypočtěte šířku intervalů a vytvořte tabulku podle toho.
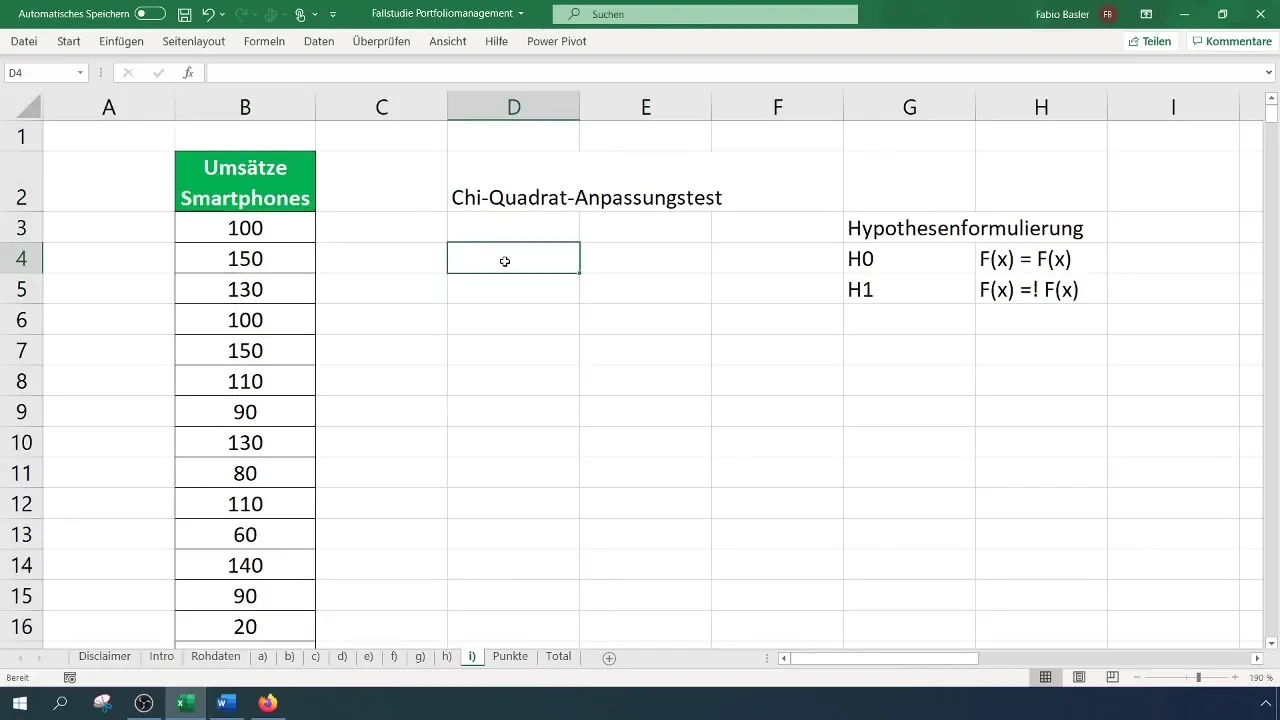
Krok 4: Výpočet frekvencí
Nyní musíte spočítat pozorované frekvence pro každou třídu. Přejděte na možnost "Data" v menu a zvolte "Histogram". Vyberte vstupní rozsah dat a třídní hranice. Určete výstupní rozsah pro tabulku četností.
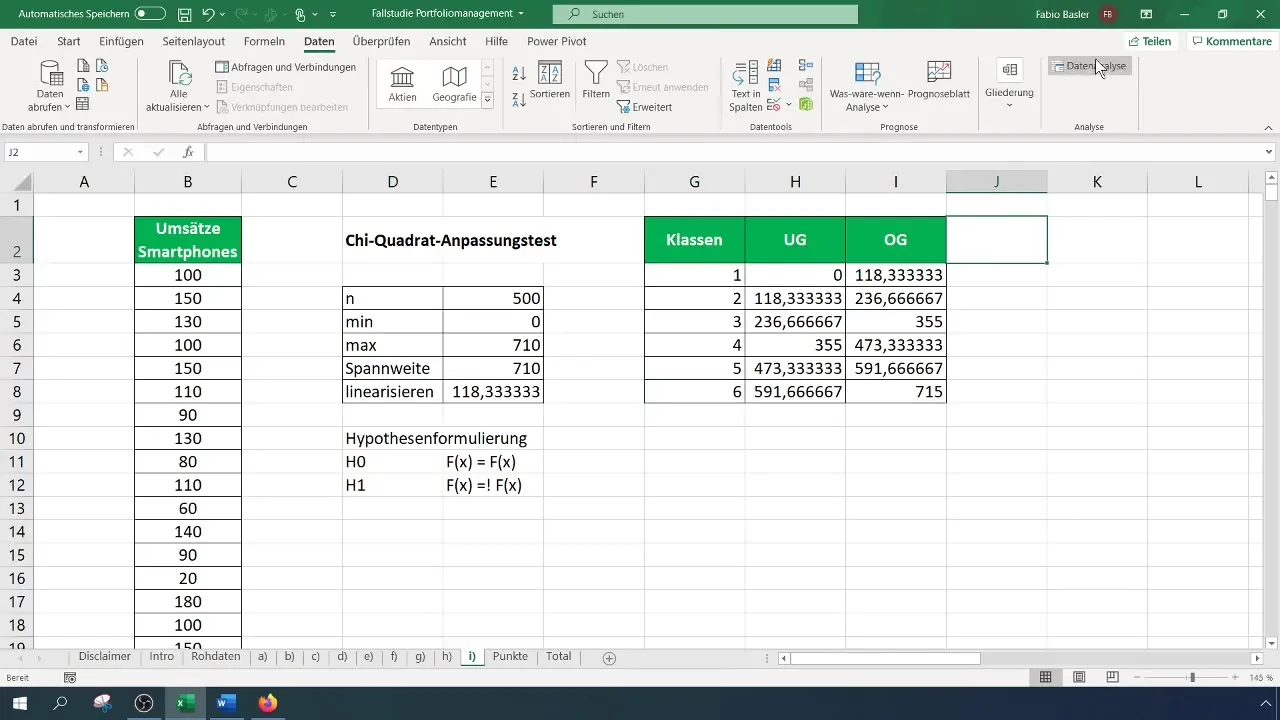
Krok 5: Výpočet očekávaných frekvencí
Pro stanovení očekávaných frekvencí vypočítejte pravděpodobnosti pro každou třídu na základě předpokládaného normálního rozdělení. K tomu potřebujete průměr a směrodatnou odchylku vašich dat.
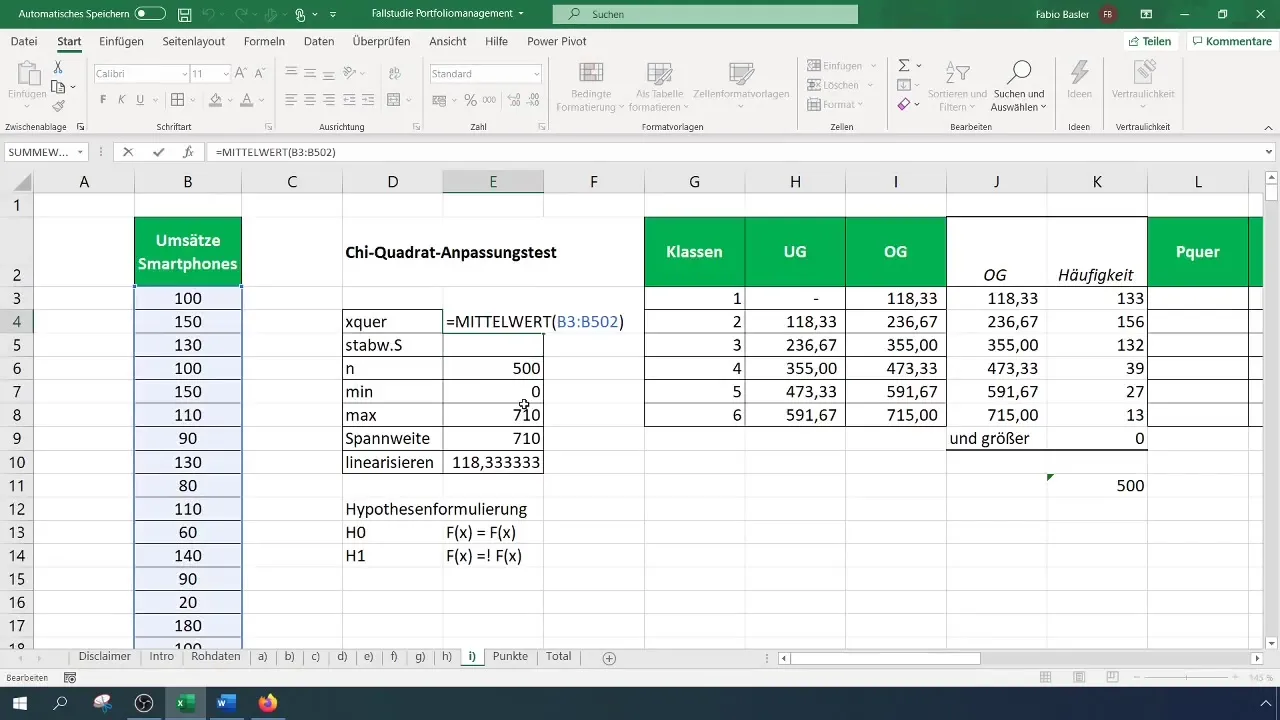
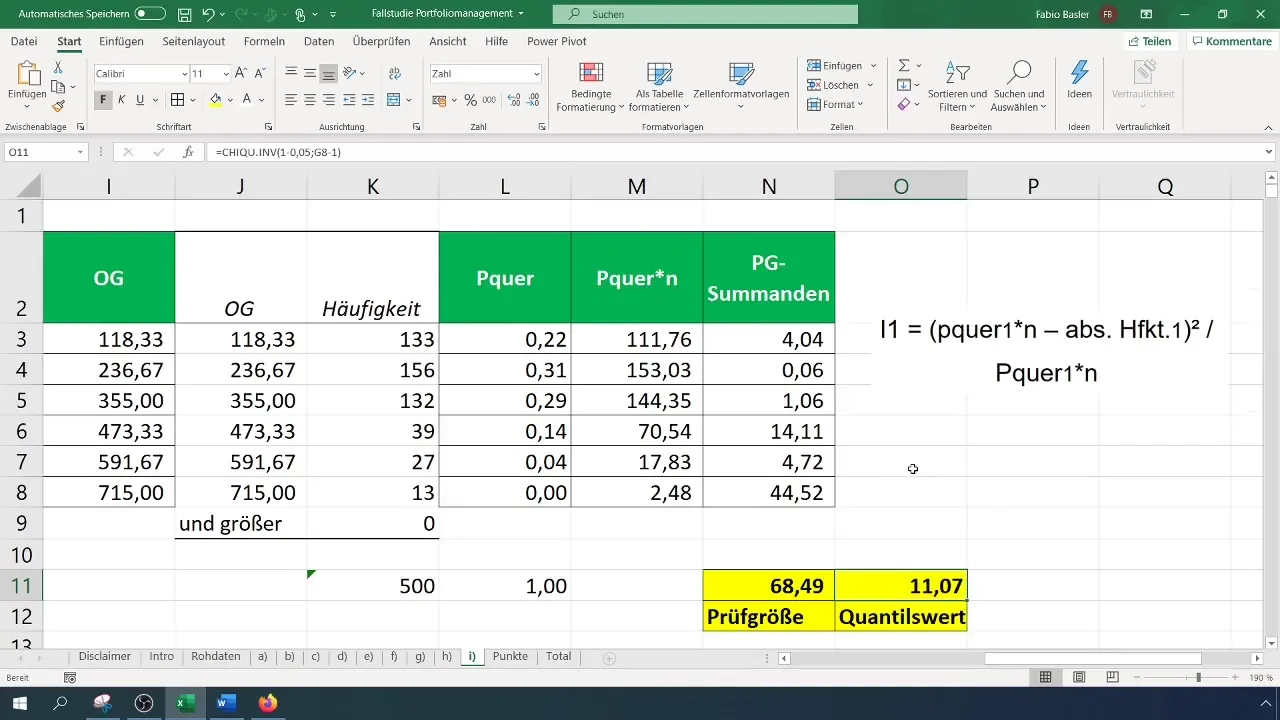
Krok 6: Výpočet testovací velikosti
Vypočítejte testovací velikost (Chi-kvadrát) podle vzorce:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
kde (O_i) jsou pozorované a (E_i) očekávané frekvence. Tuto výpočet provedete v Excelu ukládáním jednotlivých prvků do samostatných buněk.
Krok 7: Výpočet kritické hodnoty
Pro vyhodnocení testovací velikosti musíte vypočítat kritickou hodnotu ( \chi^2 ) pro váš úroveň důvěry a počet stupňů volnosti. Počet stupňů volnosti pro test Chi-kvadrát je (k - 1), kde (k) je počet tříd.
Krok 8: Ověření hypotéz
Porovnejte vámi spočtenou testovací velikost s kritickou hodnotou. Pokud je testovací velikost větší než kritická hodnota, zamítejte nulovou hypotézu, což znamená, že data nejsou normálně rozdělená. V opačném případě přijmete nulovou hypotézu.
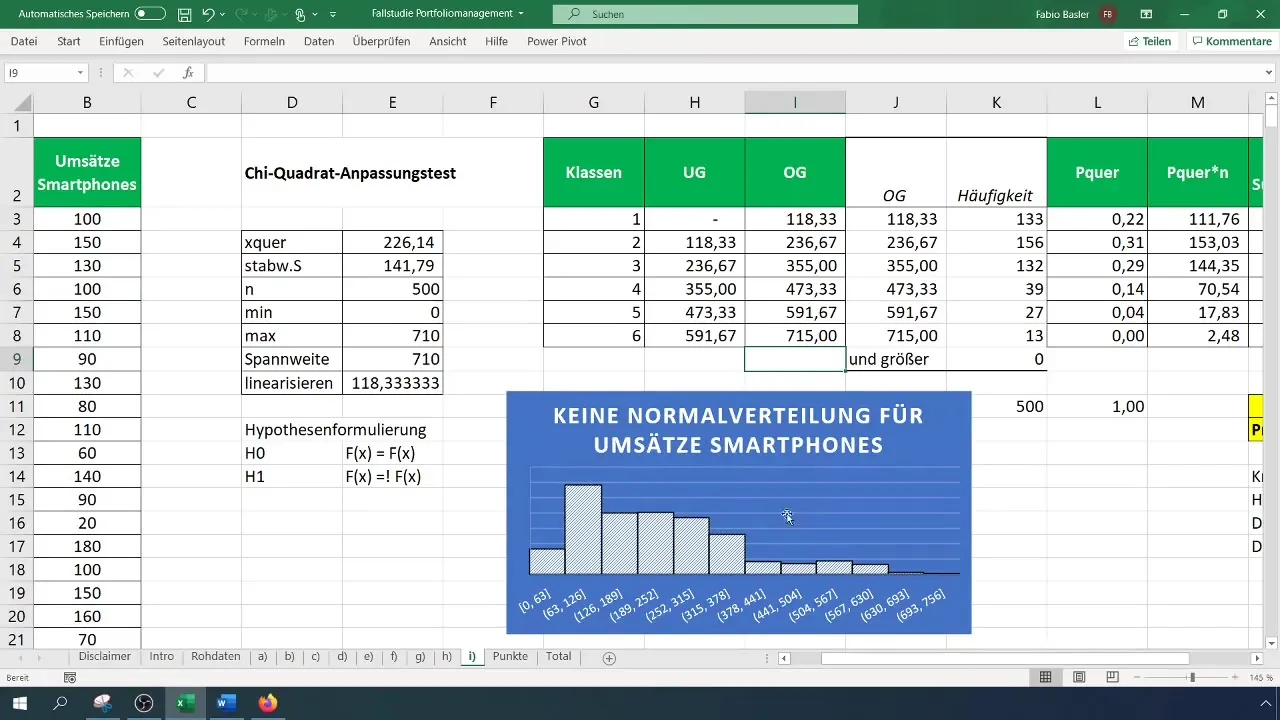
Krok 9: Shrnutí výsledků
Ukotvi své výsledky a rozšiř je o grafická data a testy hypotéz. Nezapomeň zkontrolovat svůj histogram, abys vizuálně potvrdil, že distribuce není normální.
Shrnutí
Během tohoto průvodce jsi se naučil, jak provést test přizpůsobení Chi-čtverec v Excelu k analýze normálního rozložení výnosů ze smartphonů. Kroky zahrnují vytvoření tříděné frekvence, výpočty pro očekávané frekvence, testovací statistiku a nakonec porovnání s kritickou hodnotou.


