Výpočet oboustranného konfidenčního intervalu v Excelu

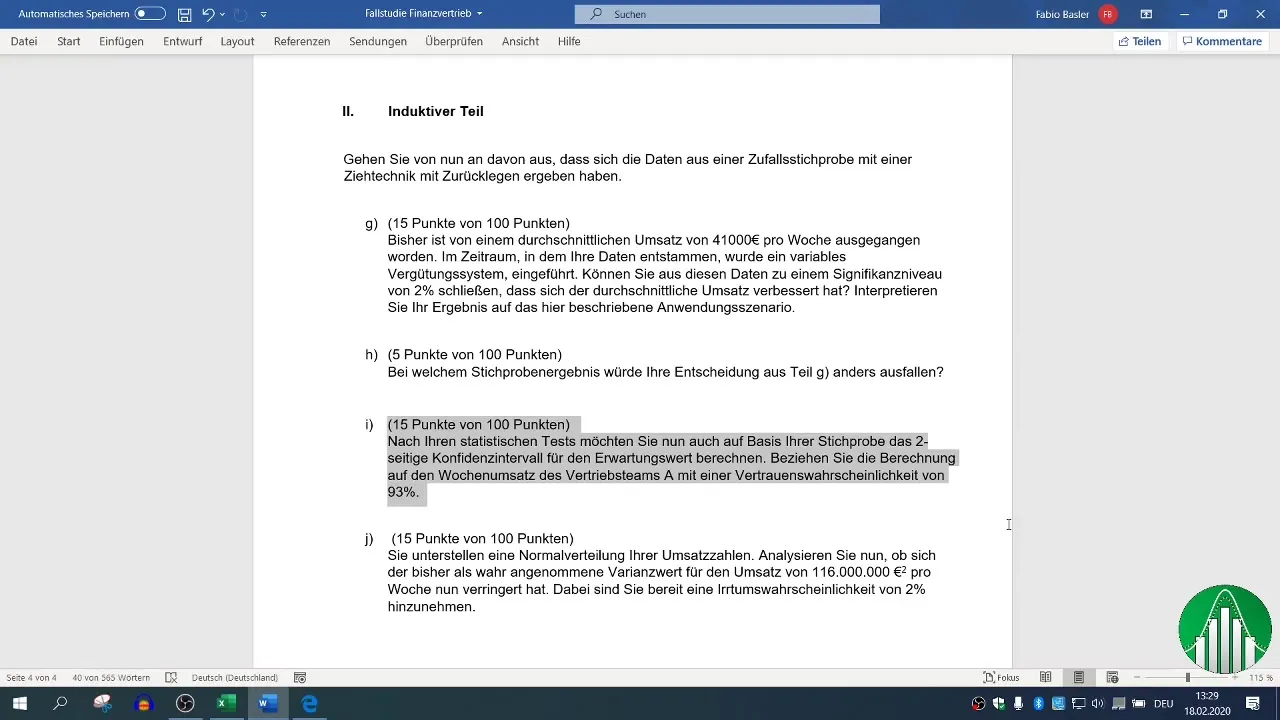
Je důležité, aby se rozhodnutí v obchodním a prodejním prostředí opírala o data analytická. Dvoustranný interval spolehlivosti ti umožní určit rozsah, ve kterém s určitou pravděpodobností najdeš skutečnou průměrnou hodnotu parametru. V tomto návodu ti ukážu, jak pomocí Exceluvypočítat rozsah intervalových hranic pro týdenní obrat prodejního týmu při důvěryhodnosti 93 %.

Nejdůležitější poznatky

K zásadním aspektům dvoustranného intervalu spolehlivosti patří:

1. Výpočet střední hodnoty jako odhadové hodnoty parametru.
2. Stanovení směrodatné odchylky ze vzorku.
3. Použití vzorců k určení dolních a horních mezí intervalu.
4. Zohlednění důvěryhodnosti k zařazení intervalu.

Krok za krokem návod

Nejdříve potřebujeme pevné porozumění termínům a krokům, které tento proces zahrnuje.

Krok 1: Příprava dat

Nejprve bys měl(a) připravit data pro tým prodejců A. Filtrovat relevantní data a zkopírovat je do svého dokumentu Excel.

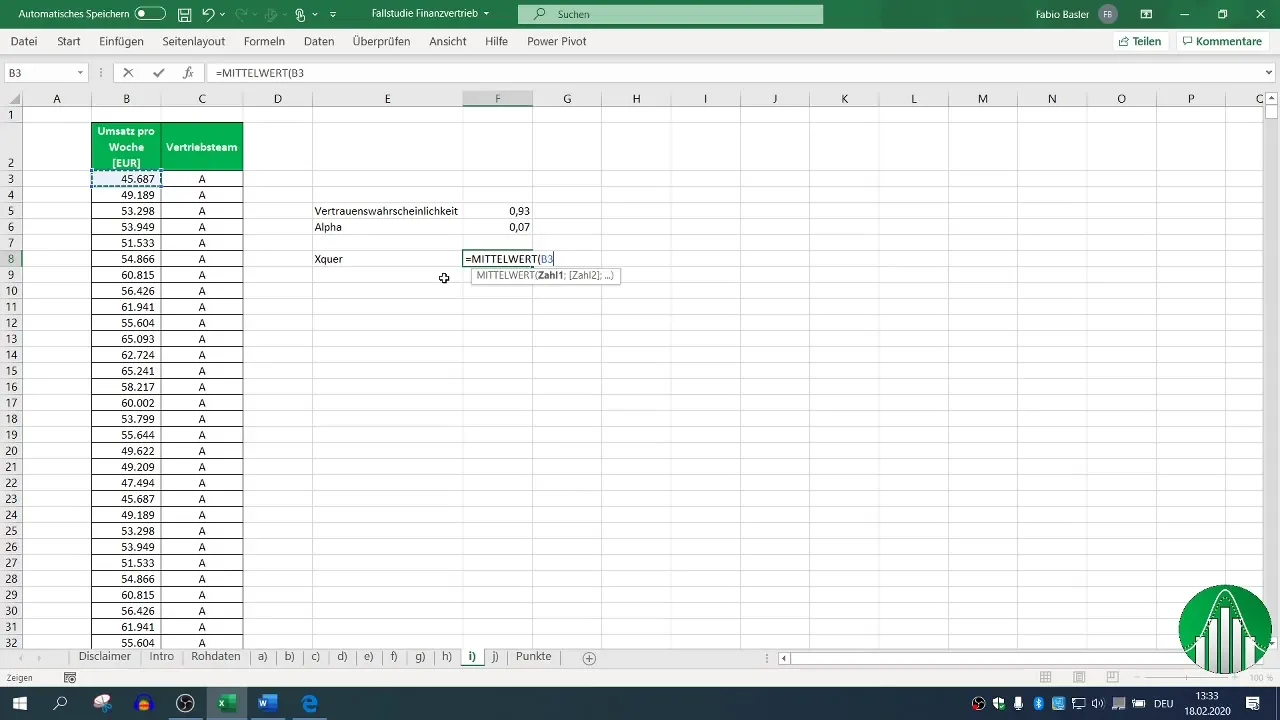
Krok 2: Výpočet střední hodnoty

Pro výpočet intervalu spolehlivosti je prvním krokem určení střední hodnoty, která slouží jako odhad pro očekávaný obrat. V Excelu můžeš použít vzorec =STŘED(Bereich) s tím, že „Bereich“ jsou buňky obsahující data o týdenním obratu týmu prodejců A.

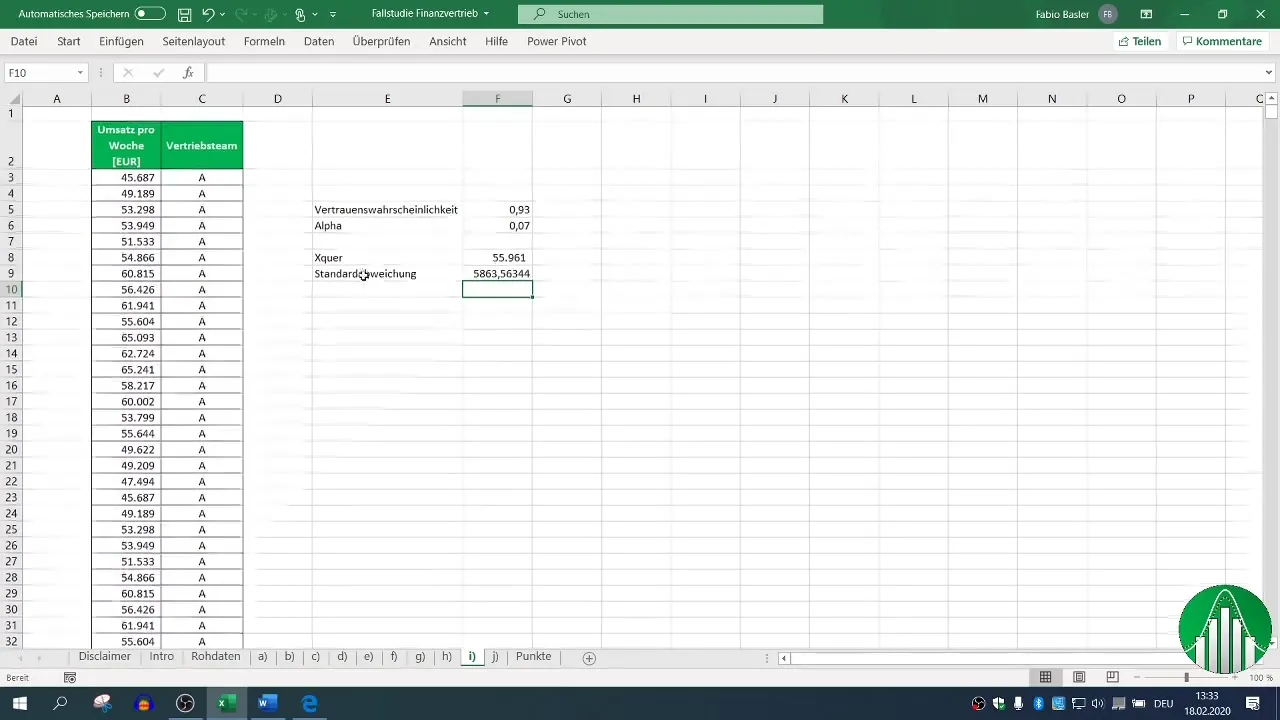
Krok 3: Výpočet směrodatné odchylky

Směrodatná odchylka (σ) je důležitá pro výpočet dvoustranného intervalu spolehlivosti. Můžeš ji v Excelu vypočítat pomocí vzorce =SČTČPATN(Bereich). Ujisti se, že zvolíš správný vzorec pro směrodatnou odchylku vzorku.

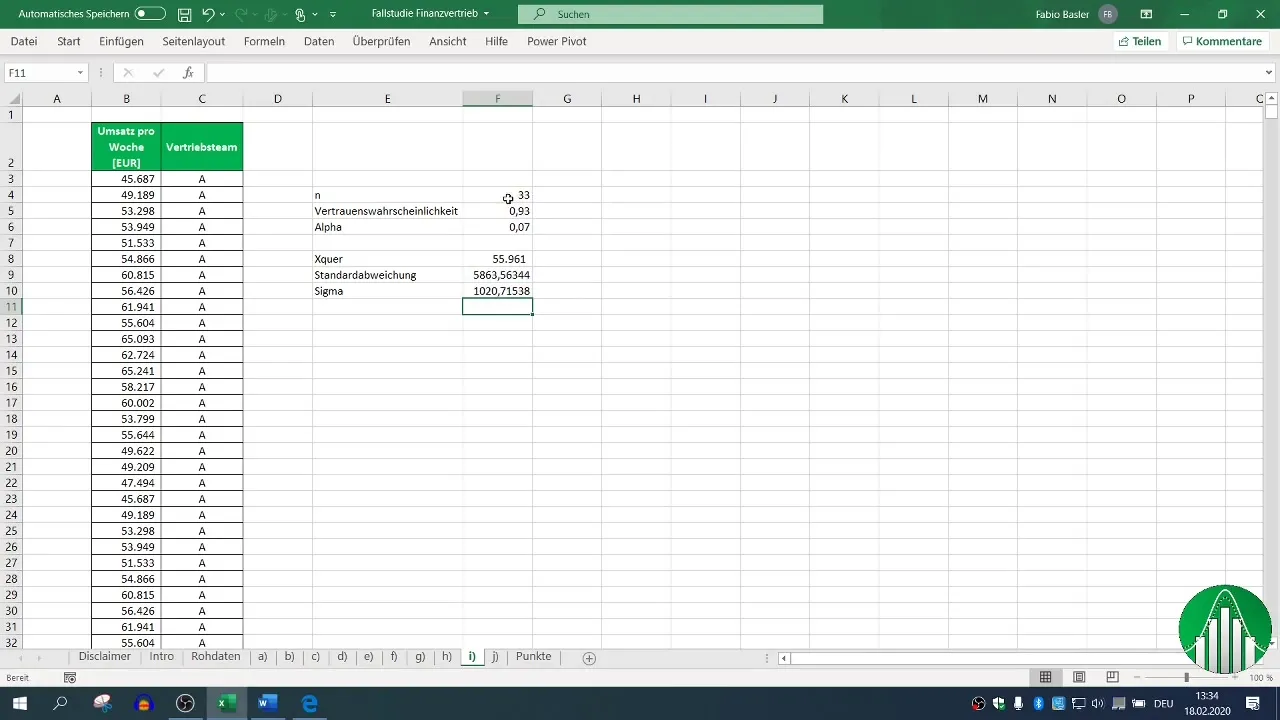
Krok 4: Stanovení velikosti vzorku

Následně musíš určit velikost vzorku (n). Sečti počet záznamů, které jsi shromáždil(a) pro prodejní tým A. V tomto případě pracujeme s předpokladem 33 záznamů.

Krok 5: Výpočet směrodatné odchylky střední hodnoty (σ_m)

Pro výpočet intervalu spolehlivosti je nezbytné spočítat směrodatnou odchylku střední hodnoty, což je jednoduše směrodatná odchylka dělená odmocninou ze vzorkového rozsahu.

Krok 6: Stanovení kvantilu

Pro výpočet dvoustranného intervalu spolehlivosti potřebuješ kvantil. Pokud uvedeš důvěryhodnost 93 %, α bude 7 % a distribuci kvantilu nalezeš pomocí funkce Excelu.

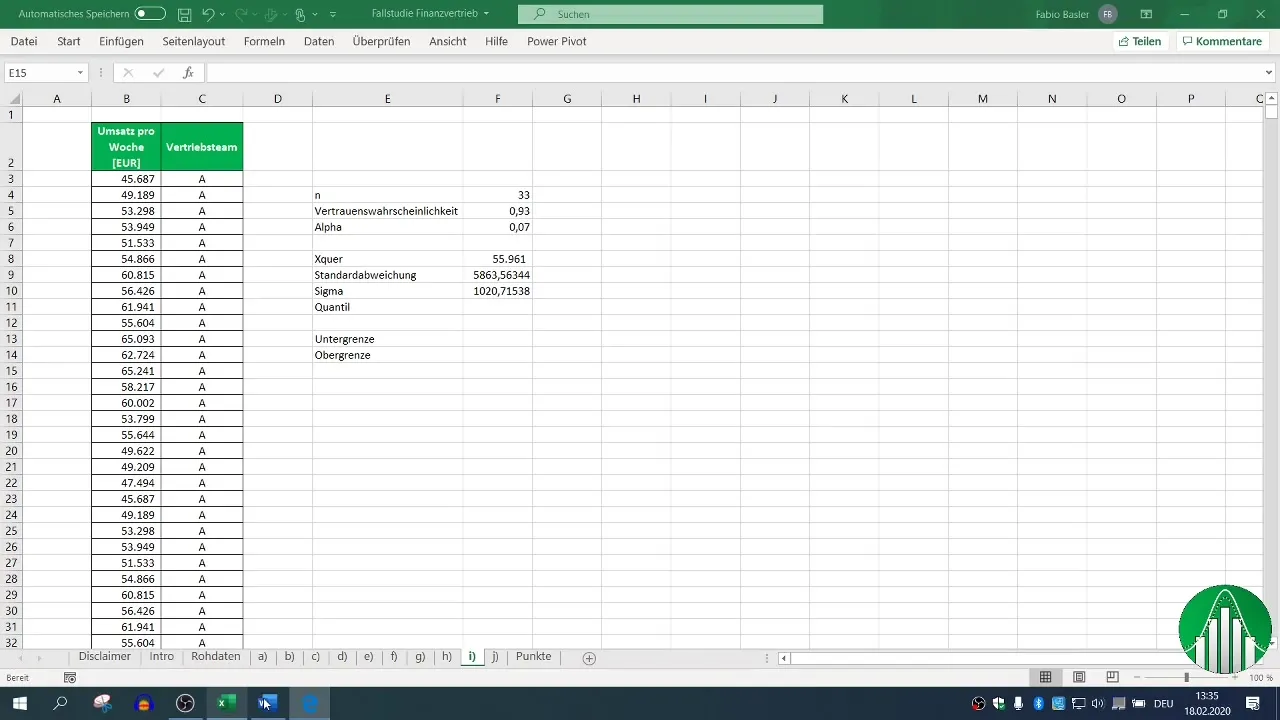
Krok 7: Výpočet dolní mez

Nyní spočítáme dolní mez intervalu spolehlivosti. Od střední hodnoty (x̄) odečtete součin kvantilu a směrodatné odchylky střední hodnoty.

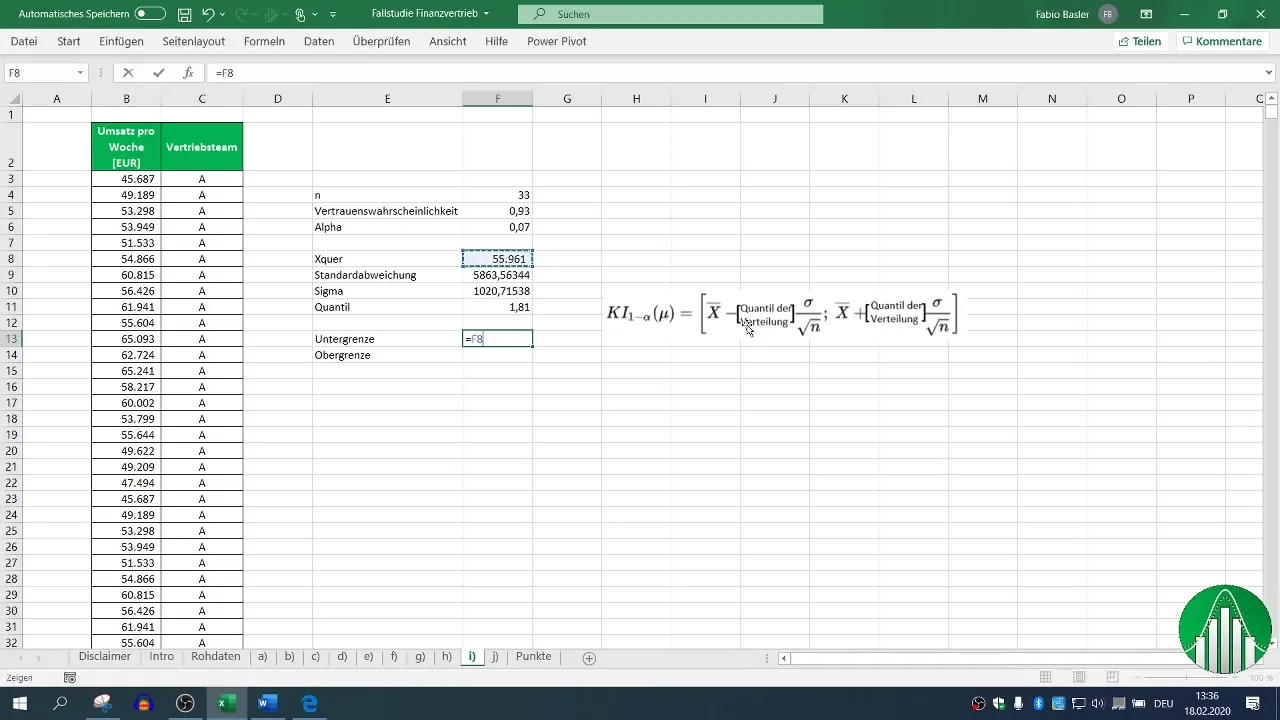
Krok 8: Výpočet horní mez

Horní mez se počítá obdobně, ale místo odečítání se provádí sčítání součinu.

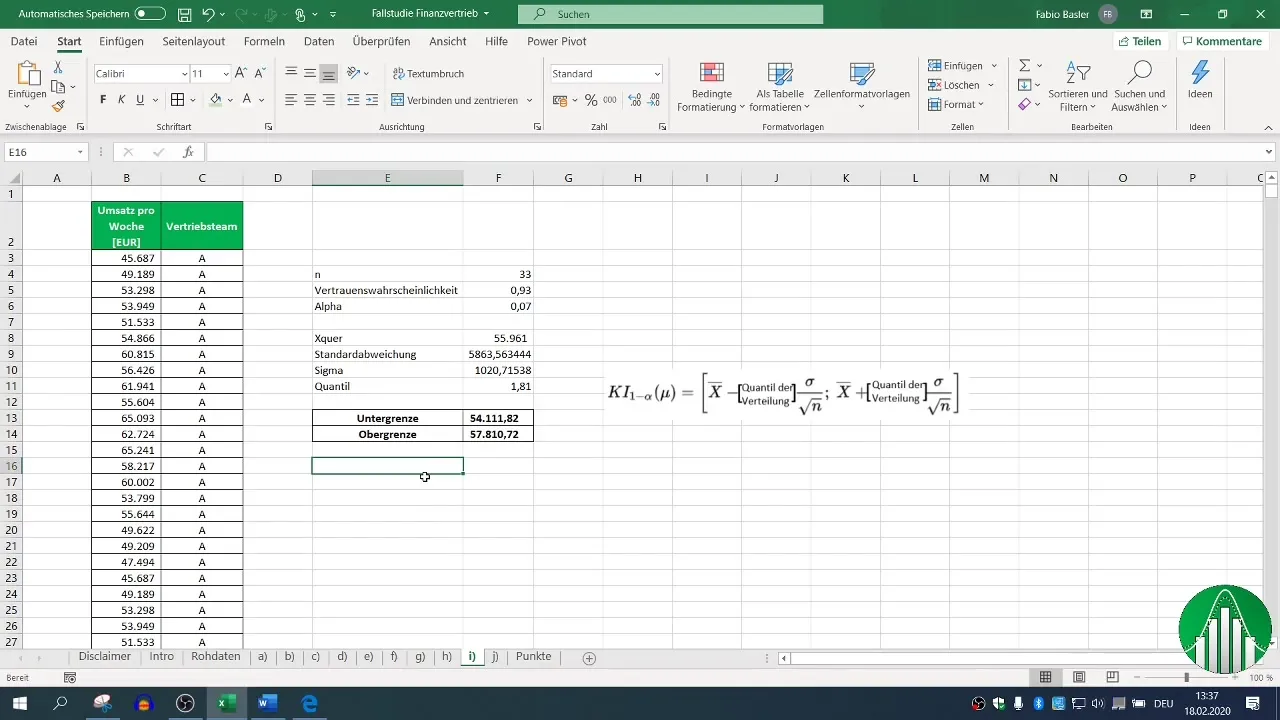
Krok 9: Interpretace výsledků

Po těchto výpočtech obdržíš dvoustranný interval spolehlivosti pro týdenní obrat prodejního týmu A. V našem příkladu se tento rozsah pohybuje mezi 54,111 a 57,810. To znamená, že s důvěryhodností 93 % je skutečná průměrná hodnota obratu v tomto rozmezí.

Shrnutí

Díky přesnému výpočtu dvoustranného intervalu spolehlivosti můžeš přesně předpovídat budoucí obrat. Naučil(a) jsi se, jak připravit relevantní data, spočítat střední hodnotu a směrodatnou odchylku a nakonec určit limity intervalu. Tímto způsobem můžeš na základě datových informací učinit rozhodnutí ve svém prodejním prostředí.