Statistické výpočty jsou nezbytnou součástí analýzy dat, zejména v prostředí elektronického obchodování. Historická datová analýza umožňuje určit pravděpodobnosti, které jsou pro podniky rozhodující. V této příručce se naučíš, jak můžeš pomocí Poissonova rozdělení pomocí Excelu spočítat pravděpodobnosti, na základě příkladu šetření.
Nejdůležitější poznatky Poissonovo rozdělení umožňuje určit pravděpodobnost událostí, které nastanou během pevně definovaného časového období. V tomto příkladu spočítáš pravděpodobnost, že více než dva, ale maximálně čtyři zákazníci zakoupí v e-obchodě během jedné hodiny něco, stejně jako pravděpodobnost, že celkově nakoupí více než dva zákazníci.
Krok za krokem návod
Začneme s výpočtem pravděpodobností pro popsané události.
Krok 1: Porozumění základům Poissonova rozdělení
Nejdříve je důležité, abys porozuměl(a), co je Poissonovo rozdělení. Toto diskrétní pravděpodobnostní rozdělení slouží k vyčíslení počtu událostí v pevných časových obdobích. V tomto aktuálním příkladu máme průměr pěti nákupů za hodinu. Tento průměr vyjadřuješ jako hodnotu λ (λ = 5).

Krok 2: Příprava dat v Excelu
Otevři Excel a připrav novou tabulku. Ujisti se, že máš relevantní parametry (λ a počet požadovaných událostí) dobře viditelné.
Krok 3: Určení pravděpodobností pro nákupy zákazníků
Pro první scénář chceš spočítat pravděpodobnost, že více než dva a maximálně čtyři zákazníci něco koupí. K tomu musíš spočítat pravděpodobnosti pro dva a čtyři zákazníky a určit jejich rozdíl.

Krok 4: Využití Excelové vzorce pro Poissonovo rozdělení
Použij funkci POISSON.PRAREPODCNA, abys spočítal(a) pravděpodobnosti. Vzorec má následující podobu:
- Pro dva nákupy: =POISSON.PRAREPODCNA(2; 5; PRD).
- Pro čtyři nákupy: =POISSON.PRAREPODCNA(4; 5; PRD).
Krok 5: Interpretace výsledků
Po použití vzorců získáš dvě pravděpodobnosti, například 12 % pro dva zákazníky a 44 % pro čtyři zákazníky. Nyní odečti pravděpodobnost pro dva nákupy od pravděpodobnosti pro čtyři nákupy, což ti dá pravděpodobnost 32 %, že více než dva, ale maximálně čtyři zákazníci něco koupí.
Krok 6: Další pravděpodobnosti spočítat
Nyní jdeš spočítat pravděpodobnost, že více než dva zákazníci nakoupí v tvém e-shopu. Nejprve spočítáš pravděpodobnost pro přesně dva nákupy a tento výsledek odečteš od 1.
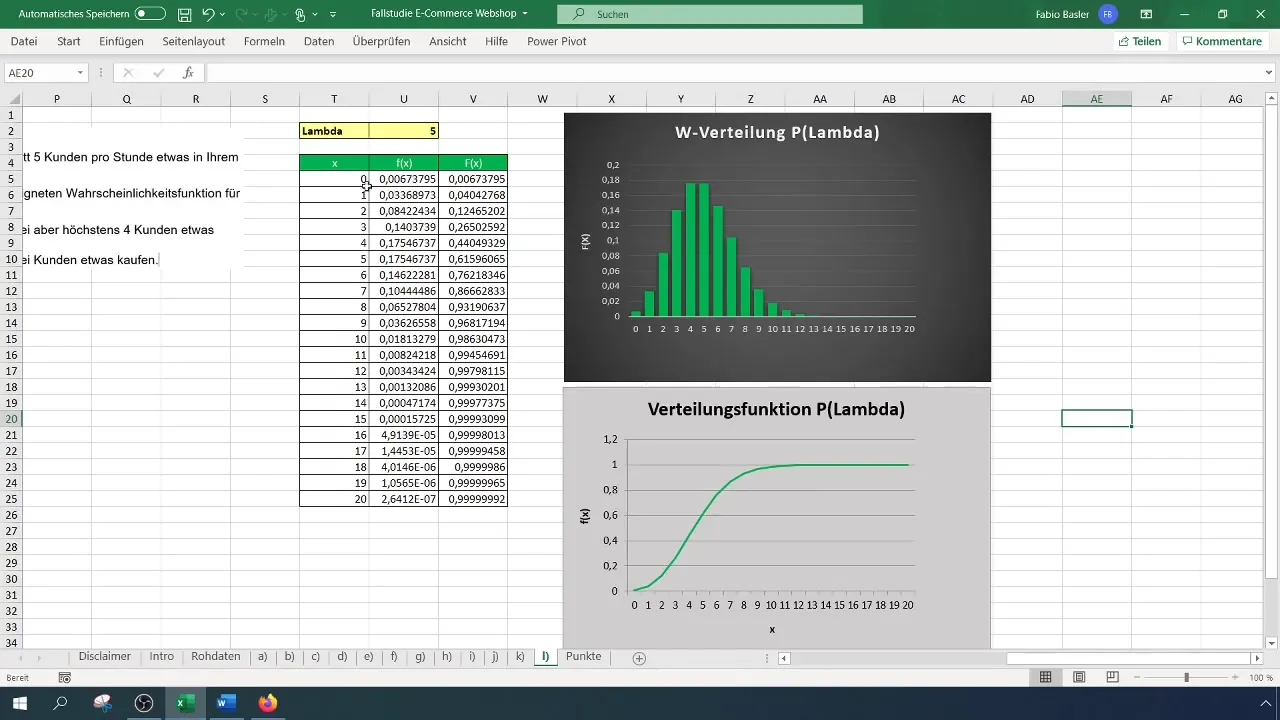
Krok 7: Využití Excelového vzorce pro více než dva nákupy
Excelový vzorec zní: =1 - POISSON.PRAREPODCNA(2; 5; PRD). Tím získáš pravděpodobnost, že více než dva zákazníci něco koupí, což v tomto případě činí 88%.
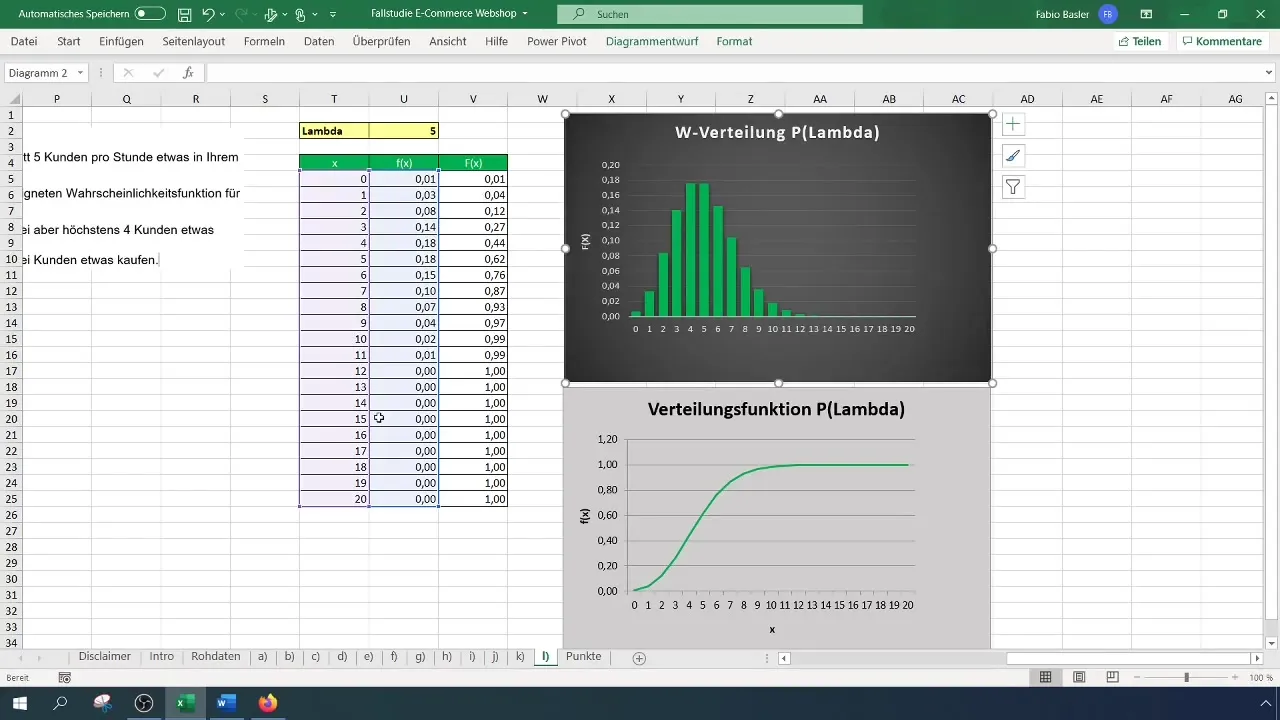
Krok 8: Shrnutí výsledků
Po provedení všech výpočtů zaznamenáš hlavní pravděpodobnosti. Zjistil(a) jsi, že pravděpodobnost, že více než dva, ale maximálně čtyři zákazníci objednají, činí 32 %, zatímco pravděpodobnost, že celkově nakoupí více než dva zákazníci, je 88 %.
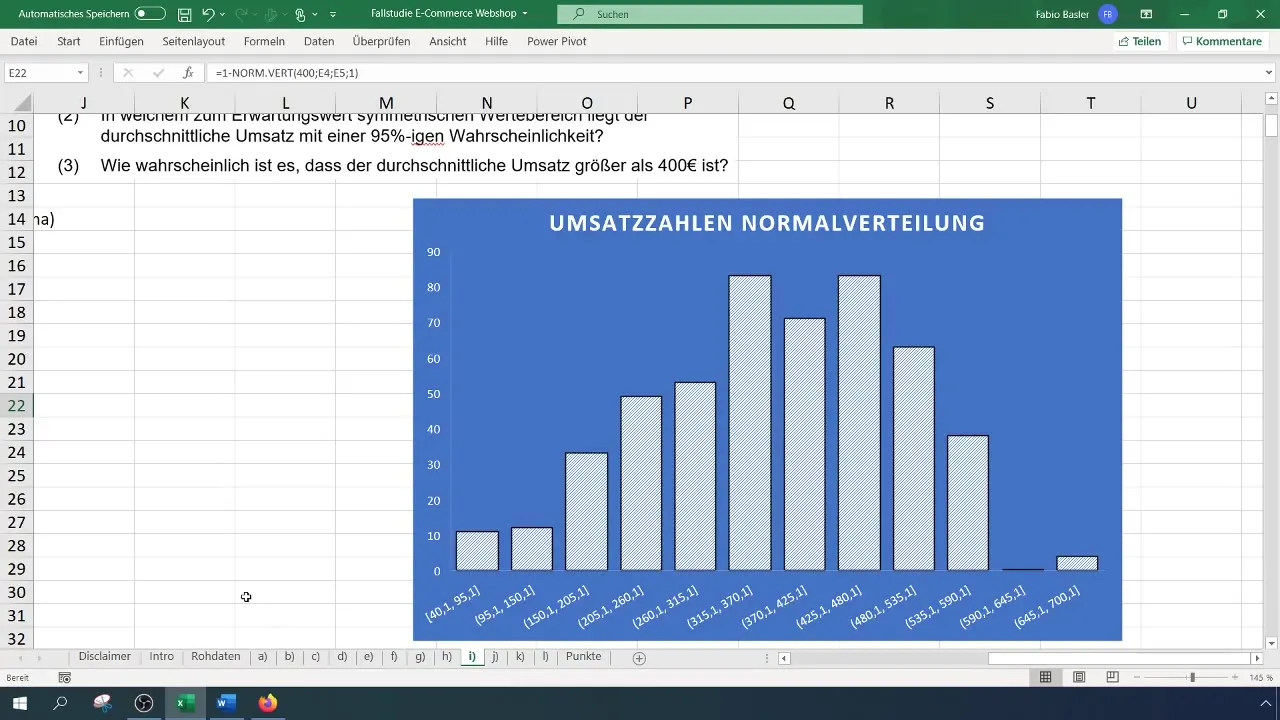
Shrnutí
V této příručce jsi se naučil(a), jak můžeš využít Poissonovo rozdělení k výpočtu pravděpodobností v Excelu. Provedl(a) jsi kroky k výpočtu a interpretaci pravděpodobností pro konkrétní události.
Často kladené otázky
Co je Poissonovo rozdělení?Poissonovo rozdělení je diskrétní pravděpodobnostní rozdělení, které udává, kolikrát se událost v pevně stanoveném časovém rámci vyskytuje.
Jak spočítám pravděpodobnosti pomocí Poissonova rozdělení v Excelu?Využiješ funkci POISSON.PRAREPODCNA k výpočtu pravděpodobností pro různé hodnoty.
Co znamená Lambda hodnota 5?Lambda hodnota 5 znamená, že průměrně nastane pět událostí (např. nákupy) ve stanoveném časovém období (např. za hodinu).
Jaké hodnoty musím zadat pro Poissonovo rozdělení?Musíš zadat počet požadovaných událostí (x), střední hodnotu (λ) a určit, zda chceš vypočítat kumulativní pravděpodobnosti.
Proč je Poissonovo rozdělení důležité pro elektronický obchod?Poissonovo rozdělení pomáhá analyzovat nákupní vzory a předpovídat pravděpodobnost zákaznických aktivit, což může podpořit důležité rozhodování v marketingu a správě zásob.


