Når du arbejder med analyse af data, vil du hurtigt støde på behovet for at erkende sammenhænge mellem forskellige variabler. I denne vejledning vil jeg vise dig, hvordan du udfører en kontingensanalyse i Excel for at kvantificere forholdet mellem to nominelle variabler. Vi vil bruge et praktisk eksempel fra bilkomponentindustrien til at forstå, hvordan man kan opnå værdifulde indsigter fra dataene.
Vigtigste indsigter
- Kontingensanalyse tillader undersøgelse af sammenhænge mellem to nominelle variabler.
- Kontingenskoefficient kvantificerer styrken af forholdet.
- En pivot-tabel i Excel er et uundværligt værktøj til analysen.
Trin-for-trin vejledning til kontingensanalyse
Trin 1: Forbered data
Før du begynder kontingensanalysen i Excel, skal du sikre, at de data, du arbejder med, er korrekt forberedt. Fjern alle filterindstillinger for at sikre fuldt overblik over dataene.
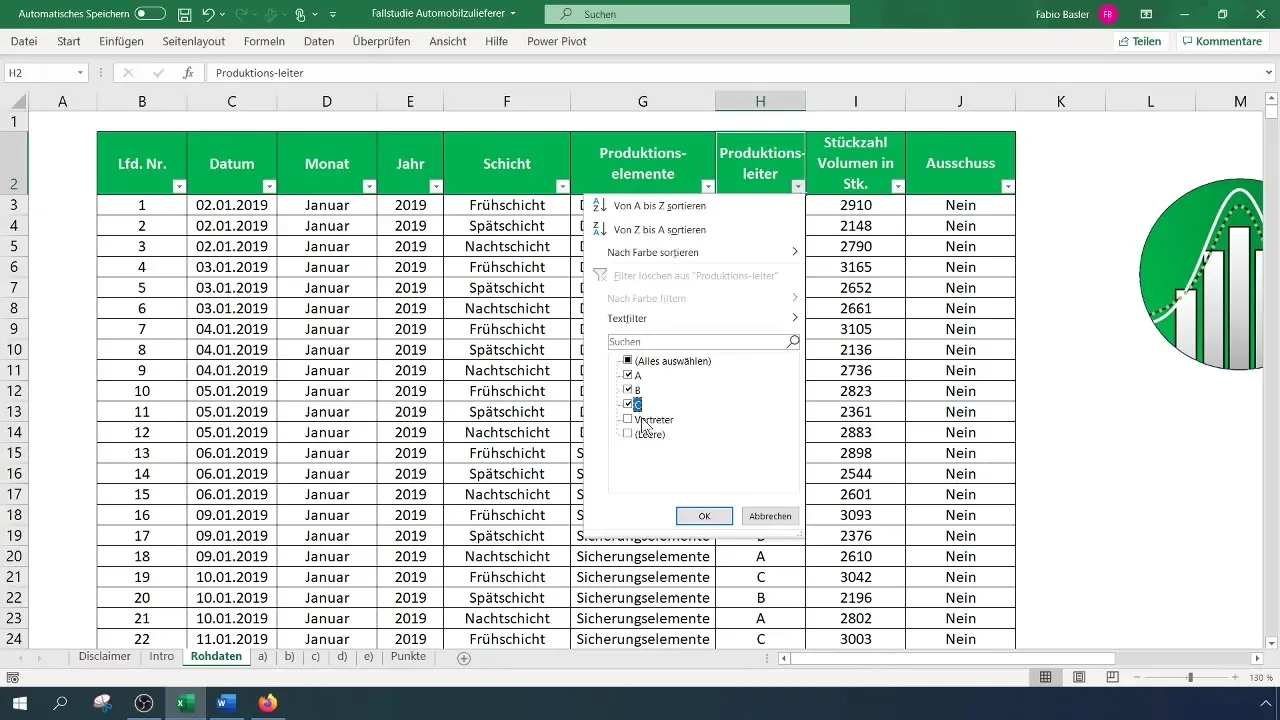
Lav en oversigt, der inkluderer produktionslederen og oplysninger om defekter som nominelle data. I vores tilfælde fokuserer vi på holdlederne A, B og C og udelader alle andre repræsentanter.
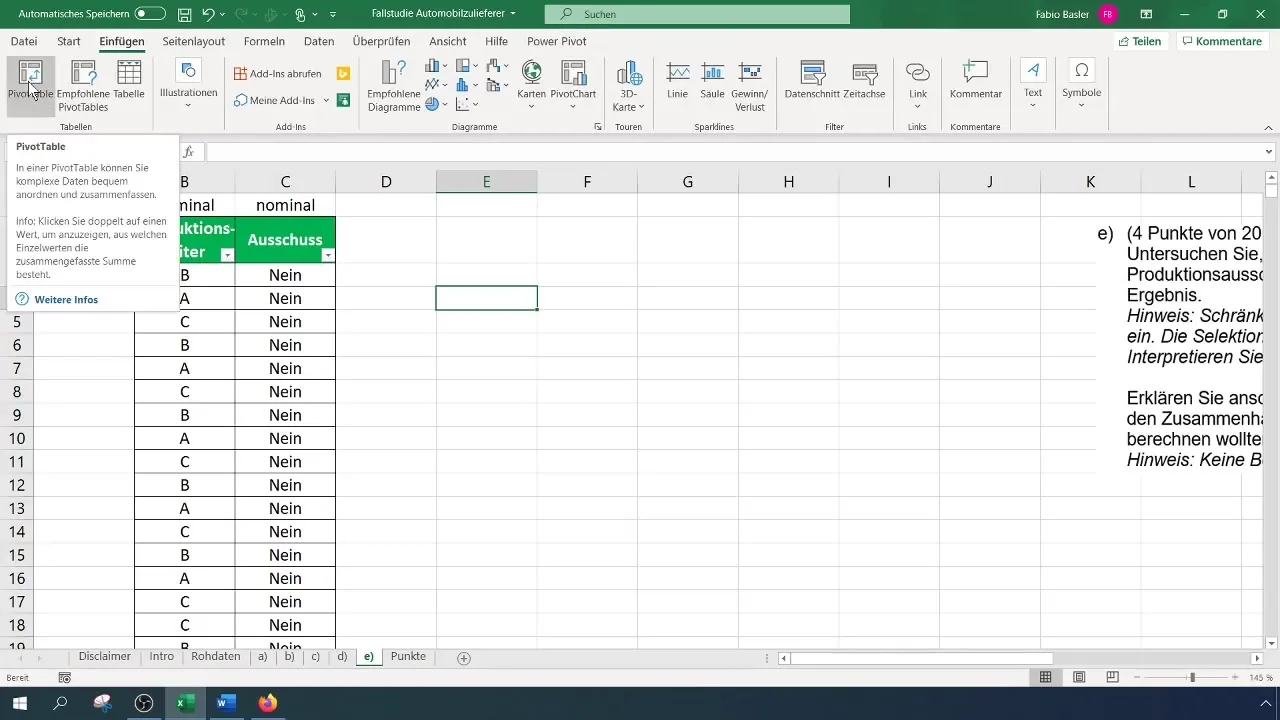
Trin 2: Opret pivot-tabel
For at udføre kontingensanalysen skal du oprette en todimensionel hyppighedsfordeling, der viser dig, hvor ofte hvert kombination af produktionsleder og defekt forekommer. Gå til menulinjen, vælg "Indsæt" og vælg "Pivottabel".
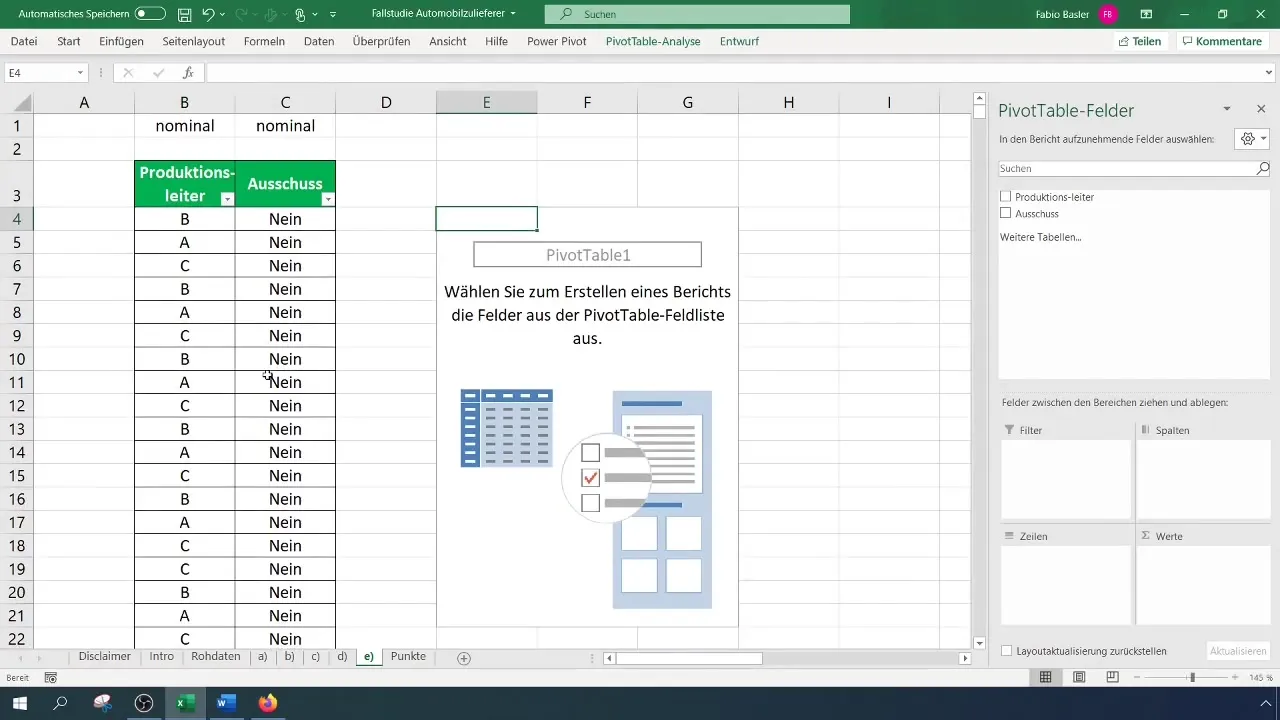
Vælg det relevante datoområde og bekræft, at overskrifterne genkendes korrekt. Din pivot-tabel oprettes nu, og du kan sammenligne felterne for produktionsleder og defekt.
Trin 3: Analyser hyppigheder
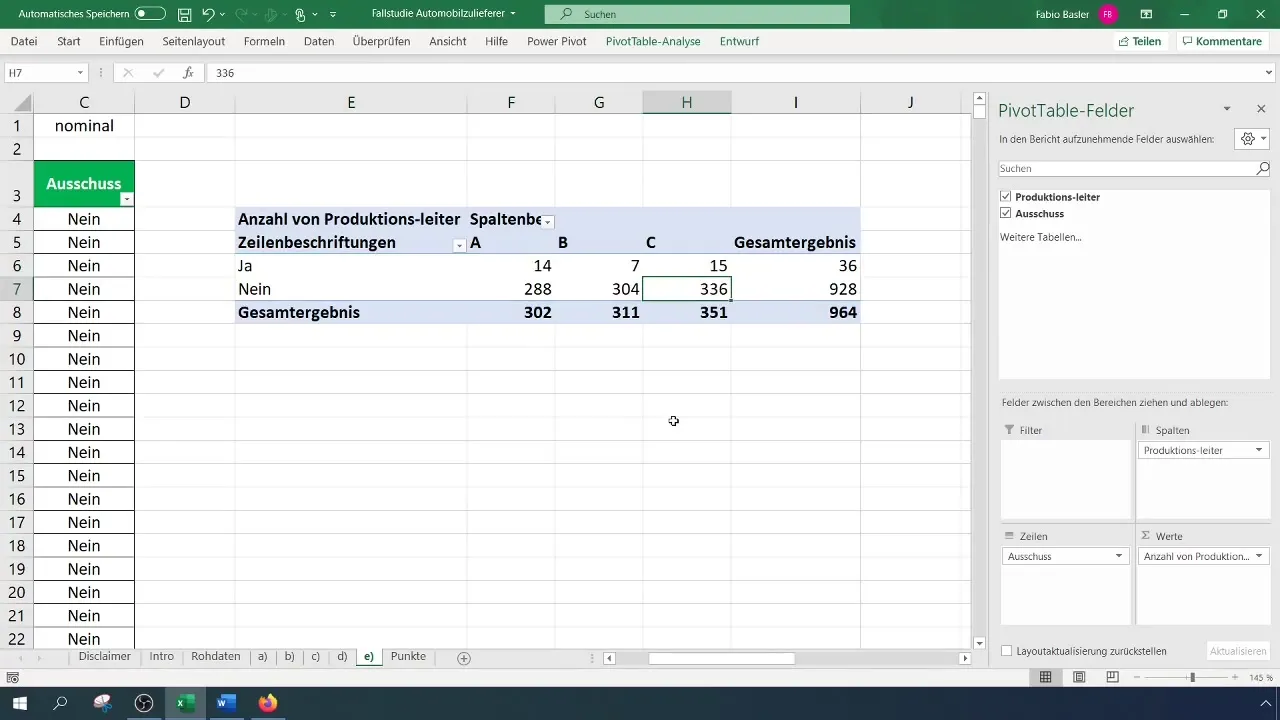
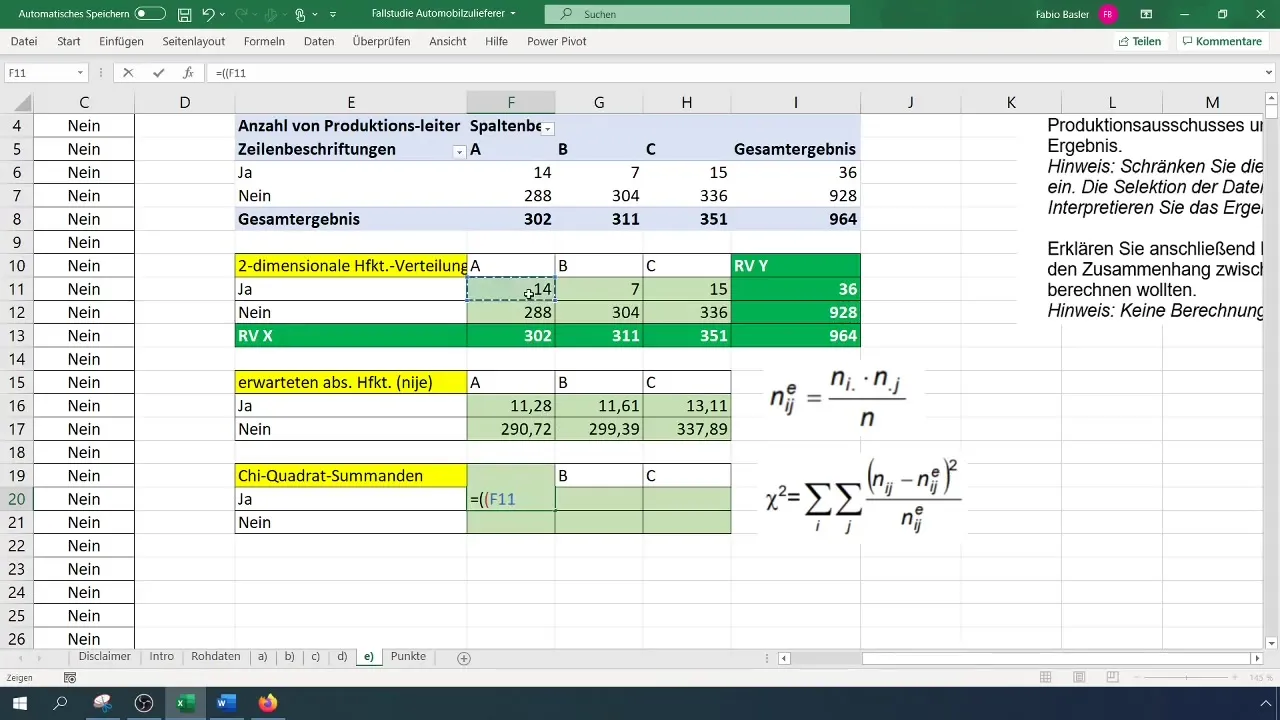
Når du har oprettet din pivot-tabel, kan du bestemme de absolutte hyppigheder. Placer kategorierne i rækker og kolonner i pivot-tabellen. Dette viser dig, hvor mange defekter der kom for hver holdleder.
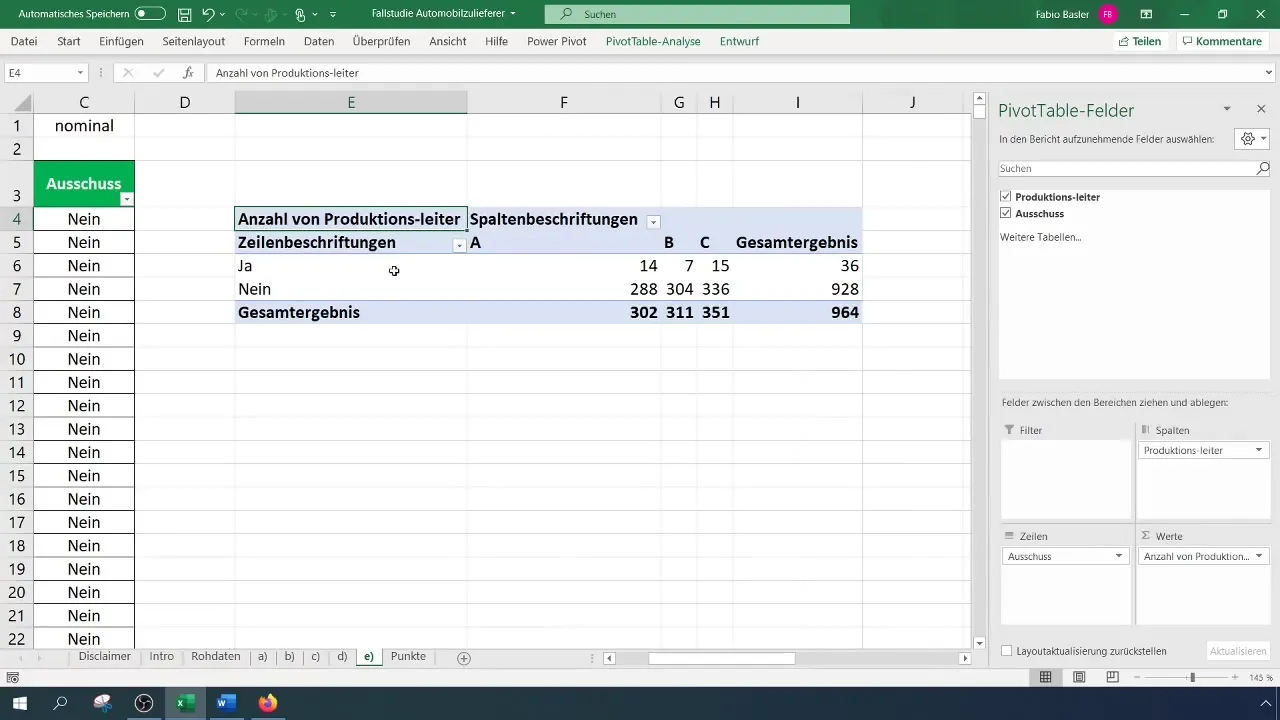
Se pivot-tabellen og analyser resultaterne. Bemærk især fordelingen af variablerne for at afgøre, hvor defekterne hyppigst eller sjældnest opstår hos hvilken holdleder.
Trin 4: Beregn forventede hyppigheder
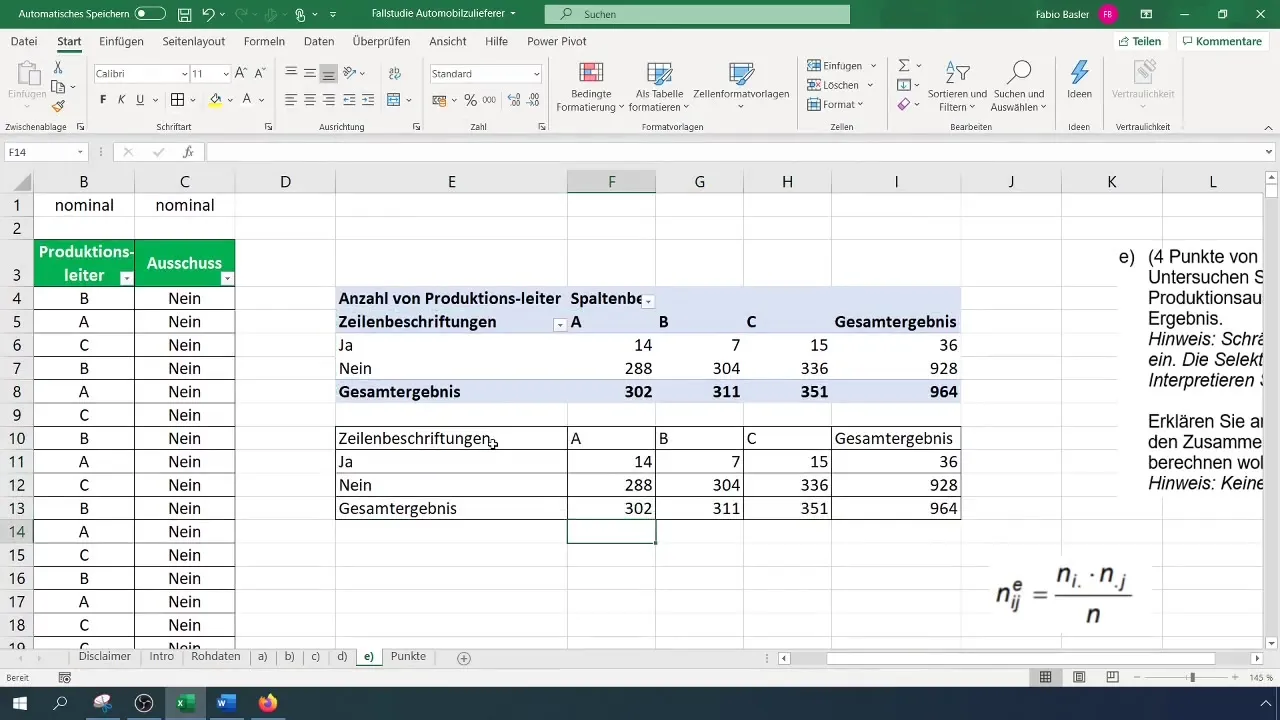
For at beregne kontingenskoefficienten skal du bestemme de forventede absolutte hyppigheder. Den generelle formel er: (N_{ij} = \frac{(R_i \times C_j)}{N}), hvor (R) er rækkehed, og (C) er kolonnehyppighed.
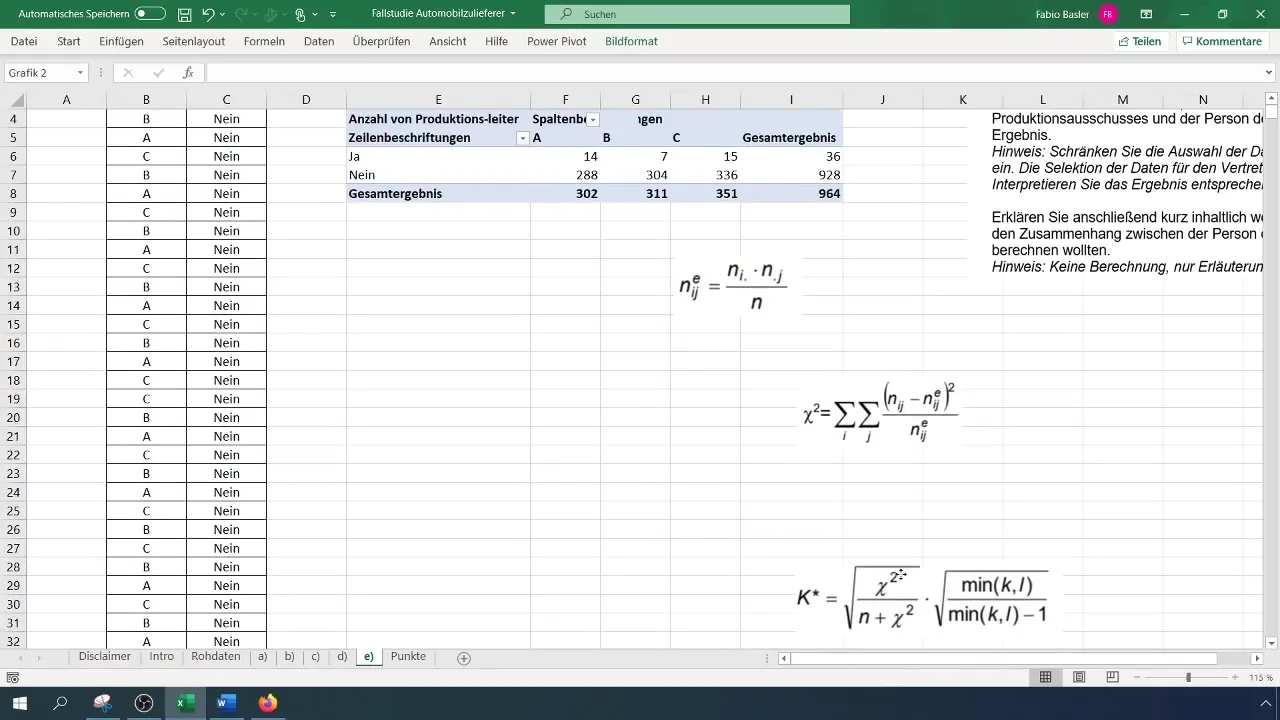
Anvend denne beregning på værdierne i din pivot-tabel. Sørg for at oprette en separat tabel til de forventede hyppigheder for at holde analysen overskuelig.
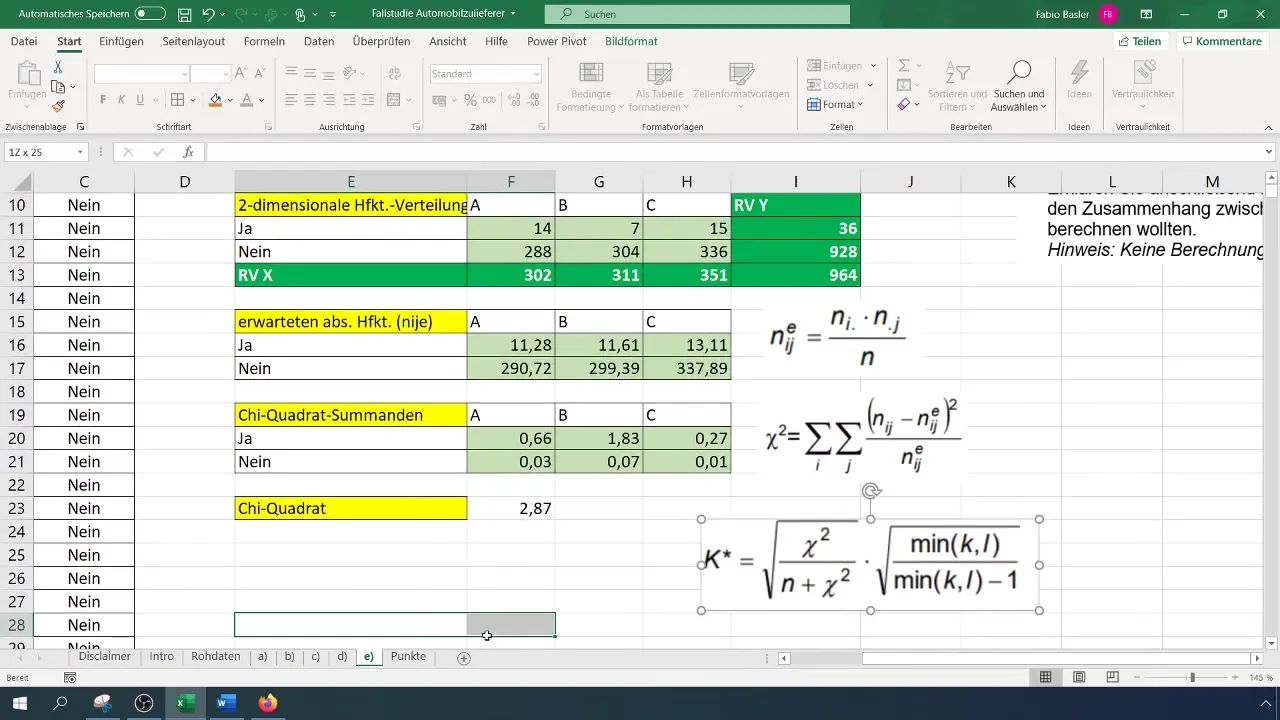
Trin 5: Beregn Chi-kvadrat-værdi
Beregn nu Chi-kvadrat-værdien for at kvantitativt vurdere forholdet mellem variablerne. Formlen er:
[ \chi^2 = \sum \frac{(O{ij} - E{ij})^2}{E_{ij}} ]
Her er (O) observeret hyppighed, og (E) er forventet hyppighed.
Beregn differencerne mellem observerede og forventede hyppigheder og kvadrer dem.
Trin 6: Beregn kontingenskoefficienter
Det sidste skridt er at beregne kontingenskoefficienten. Formlen for beregningen er:
[ K = \sqrt{\frac{\chi^2}{N}} ]
Brug den tidligere beregnede Chi-Test-værdi og det samlede antal observationer (N).
Når du har beregnet kontingenskoefficienten, kan du fortolke resultatet. Vores analyse har vist, at kontingenskoefficienten på 0,077 viser en svag sammenhæng mellem variablerne.
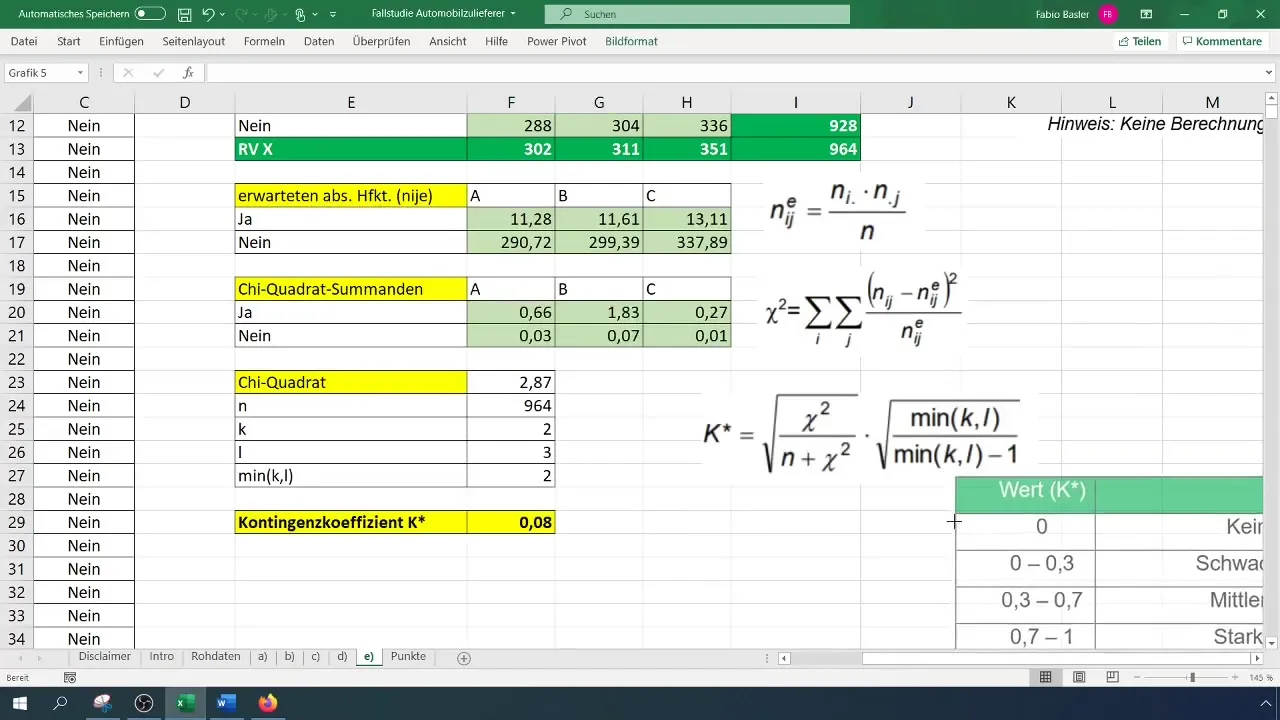
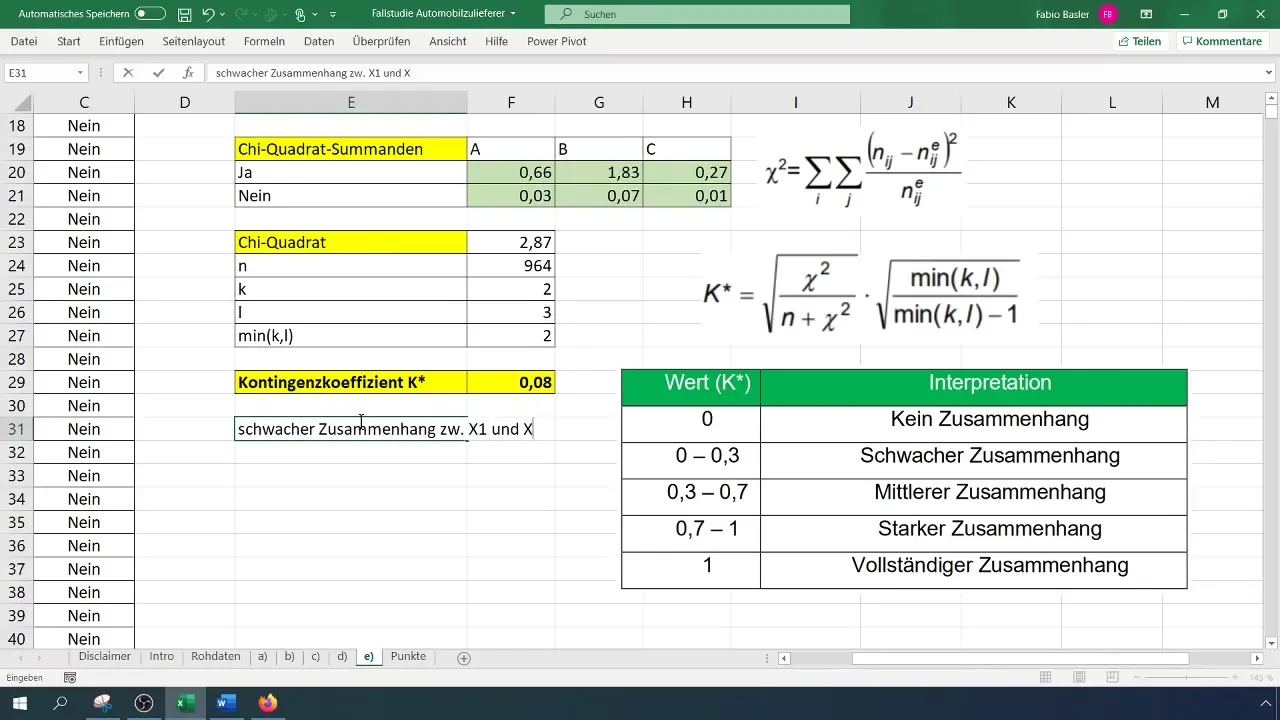
Trin 7: Fortolkning af resultaterne
De sidste trin i din analyse består i at fortolke resultaterne. En kontingenskoefficient tæt på 0 indikerer, at der næsten ikke er nogen sammenhæng mellem variablerne. En værdi på 0,08 antyder, at produktionslederen ikke har nogen signifikant indflydelse på forekomsten af fejl.
Opsamling
I denne vejledning har du lært, hvordan du udfører kontingensanalyse i Excel for at identificere sammenhænge mellem nominelle variabler. Du har lært, hvordan du forbereder dine data, opretter en pivottabel og udfører de nødvendige beregninger for kontingenskoefficienten.
Ofte stillede spørgsmål
Hvordan håndterer jeg store datamængder?Hvis du arbejder med mange variable, skal du klassificere dataene i grupper for at forenkle analysen.
Kan jeg udføre kontingensanalyse i andre softwareværktøjer?Ja, grundprincipperne for kontingensanalyse er anvendelige i mange statistiksoftware og programmeringssprog, selvom trinene kan variere.
Hvilke variable er egnet til kontingensanalyse?Nominelle variable er ideelle til denne type analyse, da de ikke har en rangorden.
Hvordan tolker jeg kontingenskoefficienten?En værdi mellem 0 og 0,3 indikerer en svag sammenhæng, mellem 0,3 og 0,6 en moderat sammenhæng, og over 0,6 en stærk sammenhæng.


