Statistiske tests er en central del af dataanalyse og beslutningstagning. Især inden for bioteknologi kan det være afgørende at teste hypoteser om succesraten af aktive stoffer. I denne vejledning lærer du, hvordan du effektivt udfører en en-stikprøve test (1-SP-test) for forventningsværdien med kendt varians i Excel.
Vigtigste resultater
Denne vejledning vil lære dig:
- De teoretiske grundlag for 1-SP-testen.
- Trin til udførelse af testen i Excel.
- Fortolkning af resultaterne.
Forberedelse af data
For at udføre en 1-SP-test i Excel skal du først have de relevante data. I vores eksempel antager vi en situation, hvor du analyserer succesraten af aktive stoffer. Det er kendt, at den gennemsnitlige succesrate tidligere var 59%, med en standardafvigelse på 19. Begynd med at indtaste dine data i en Excel-tabel.
Sørg for at organisere dine data i kolonner, så du let kan få adgang til dem senere. En god struktur vil hjælpe dig med bedre at følge de enkelte trin.
Testoversigt
1-SP-testen bruges til at kontrollere, om den gennemsnitlige succesværdi adskiller sig markant fra en forudbestemt værdi. I dette tilfælde kontrollerer vi, om succesraten på 59% kan øges markant i fremtiden.
Formulering af hypoteser
De hypoteser, du opstiller for testen, er afgørende:
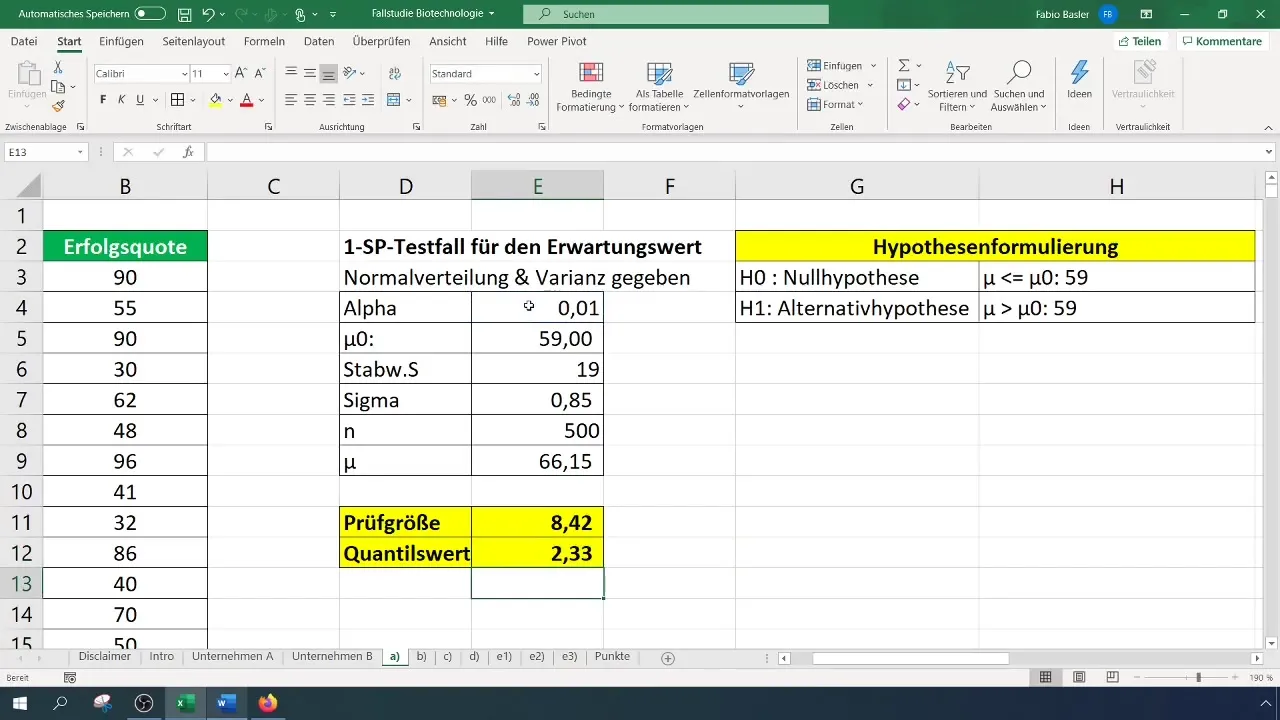
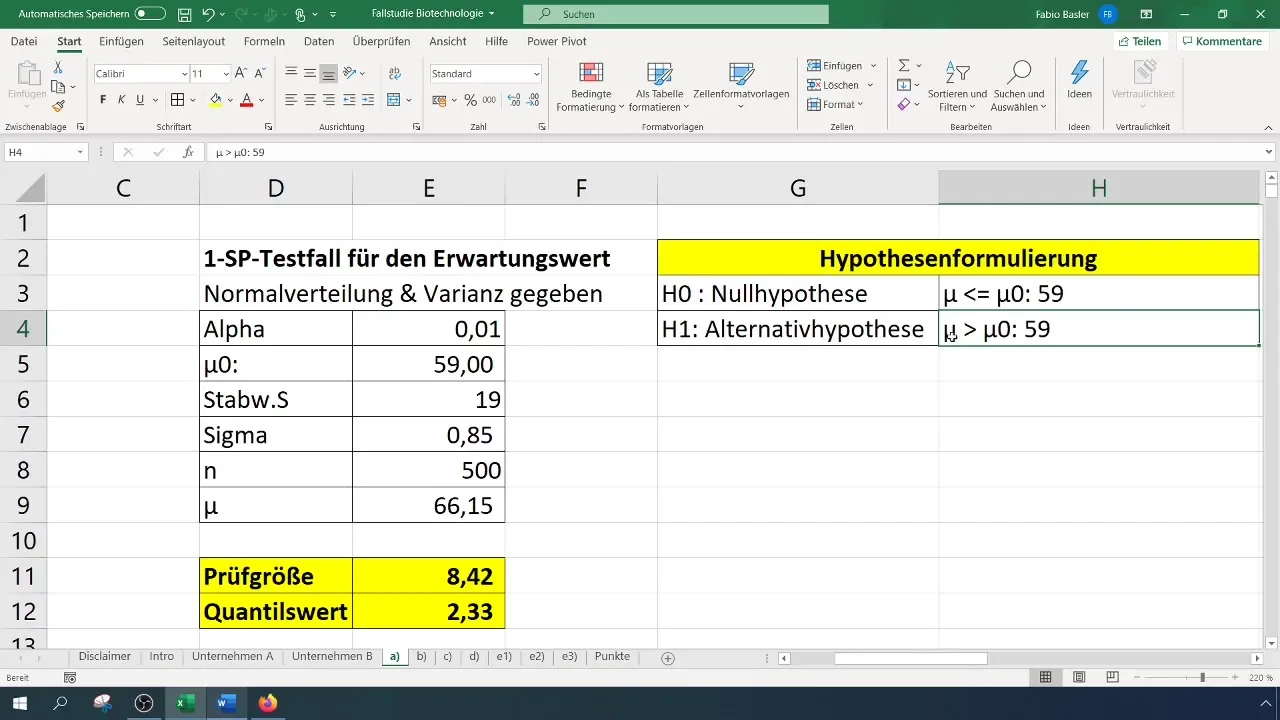
- Nulhypotese (H0): Den sande forventningsværdi er lig med 59 (σ = 59%).
- Alternativhypotese (H1): Den sande forventningsværdi er større end 59%.
Ved formulering af hypoteserne bør fokus være på, hvad der nøjagtigt skal testes, og hvordan det udtrykker sig i din sammenhæng.
Det er vigtigt at kunne skelne klart mellem nulhypotesen og alternativhypotesen, da de danner grundlaget for de følgende beregninger.
Indsamling af stikprøven
Til vores test tager vi en stikprøve på 500 aktive stoffer. Det er vigtigt at bemærke, at udvælgelsen af stikprøven bør være repræsentativ og bør med den passende metode sikre, at dine resultater realistisk set kan overføres til den samlede population.
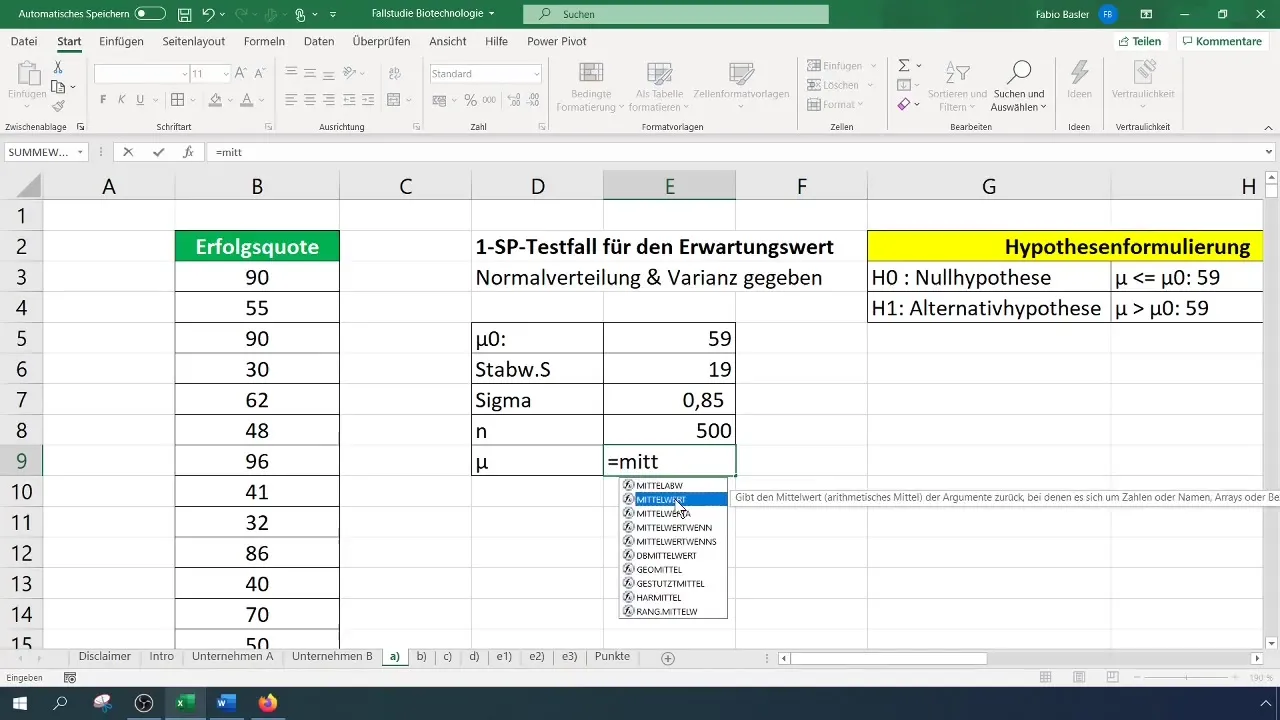
Til testen beregner du først det aritmetiske gennemsnit. Dette kan nemt gøres ved at anvende den relevante formel i Excel.
Beregning af teststørrelse
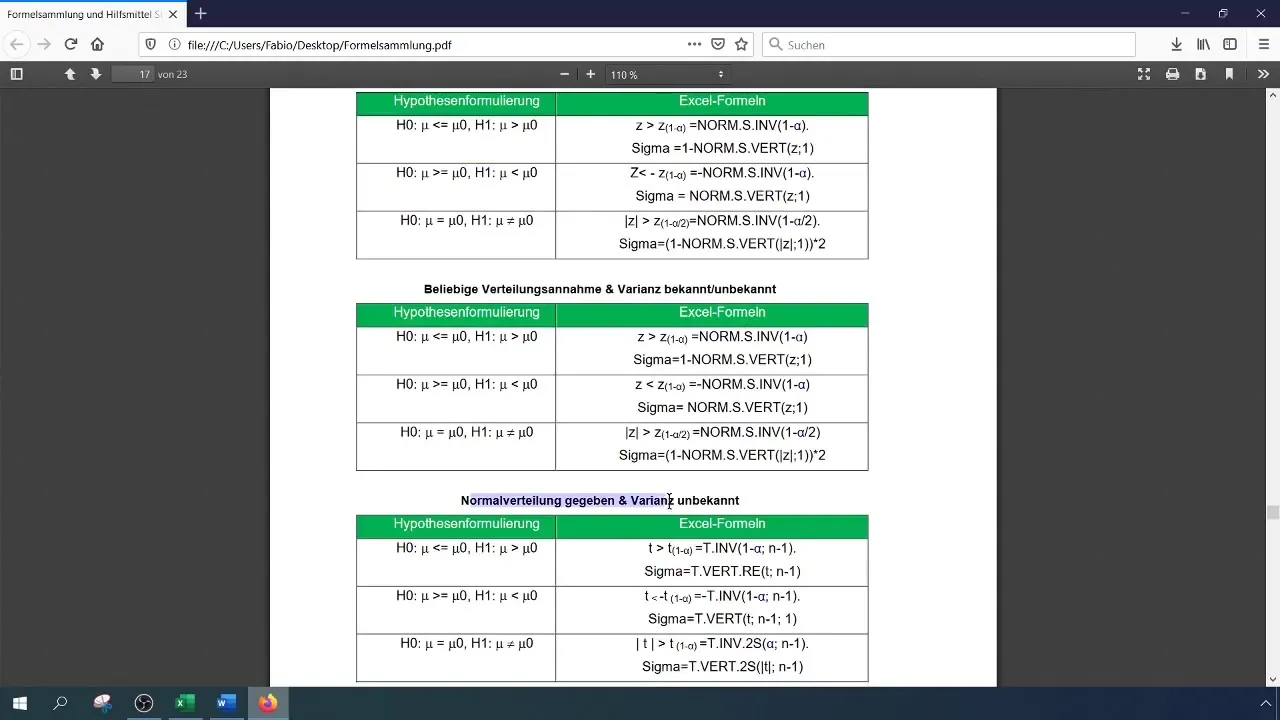
Teststørrelsen for en 1-SP-test bestemmes ved følgende formel:
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Her repræsenterer (\bar{x}) gennemsnittet af din stikprøve, (\mu_0) den antagne middelværdi (i dette tilfælde 59), (\sigma) standardafvigelse (her 19), og (n) antallet af stikprøver (500).
Når du har indsat værdierne i formlen, beregn teststørrelsen for at afgøre, om den er signifikant eller ej.
Bestemmelse af kritisk værdi
For en signifikansgrad på 1% (0,01) skal du aflæse eller beregne den kritiske værdi. Dette kan gøres i Excel ved hjælp af funktionen NORM.S.INV.
Formlen er som følger:
[ \text{NORM.S.INV}(1 - \alpha) ]
Her er (\alpha) signifikansniveauet (0,01). Den beregnede værdi bruges som grundlag for sammenligningen med teststørrelsen.
Udførelse af testen
Når du har både teststørrelsen og den kritiske værdi, sammenligner du dem:
- Hvis teststørrelsen er større end den kritiske værdi, forkastes nulhypotesen.
- Ellers kan du ikke afvise nulhypotesen.
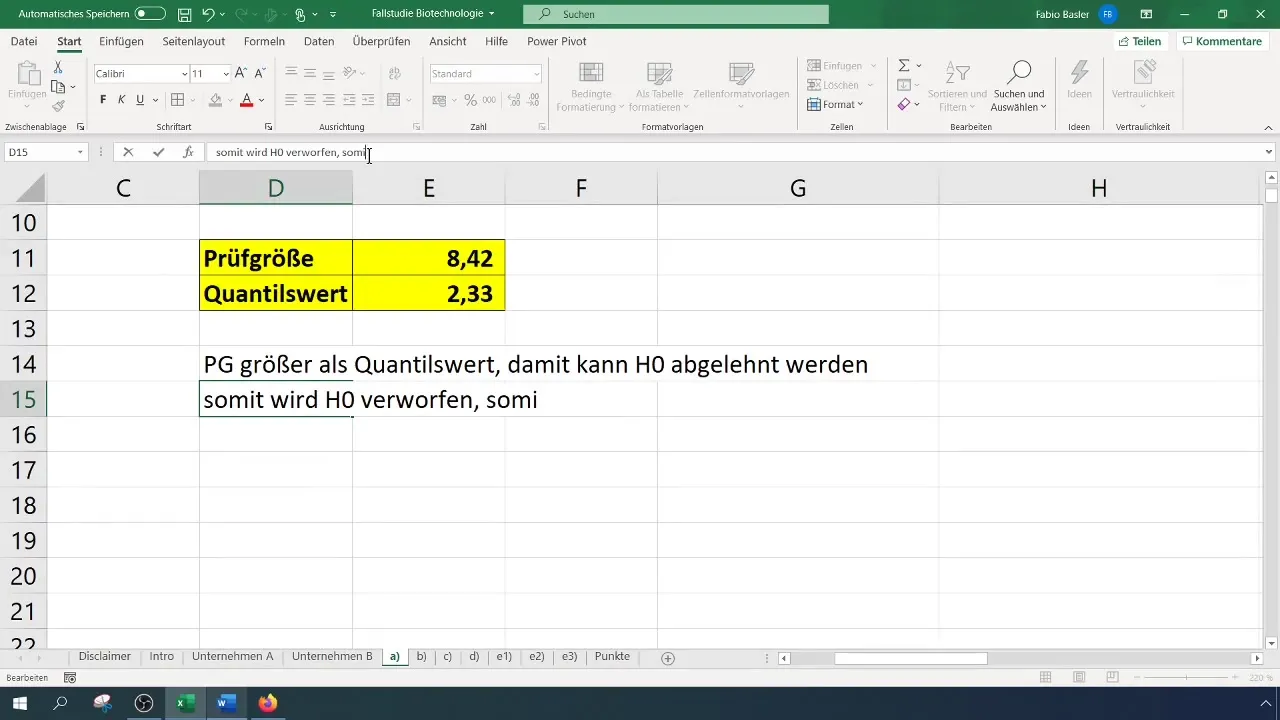
I vores tilfælde resulterer i en teststørrelse på 8,4, som overskrider den kritiske værdi på 2,33. Derfor kan vi afvise nulhypotesen. Dette tyder på, at succesraten er signifikant forbedret.
Tolkning af resultaterne
Efter at have udført testen og identificeret resultaterne, bør du tolke dem i en klar sammenhæng. Afvisningen af nulhypotesen betyder, at den testede nye værdi er signifikant forskellig fra fortiden, i dette tilfælde 59%.
Disse oplysninger er af enorm betydning for strategisk beslutningstagning i din virksomhed. De bekræfter, at bestræbelserne på at forbedre succesraten har været effektive.
Resume
I denne vejledning har du lært, hvordan du udfører en 1-SP-test for forventningsværdien i Excel. Med en case-studie kunne du følge trinnene fra opstilling af hypoteser og data beregning til fortolkning af resultaterne. Disse færdigheder er værdifulde ikke kun for videnskabelige evalueringsformål, men også for praktiske anvendelser i virksomheden.
Ofte stillede spørgsmål
Hvad er 1-SP-testen?1-SP-testen er en statistisk test for at kontrollere, om gennemsnittet af et udsnit afviger signifikant fra en forudbestemt værdi.
Hvordan formulerer jeg hypoteser for testen?Hypoteserne består af en nulhypotese (H0) og en alternativ hypotese (H1), der dokumenterer den tilstand, der skal kontrolleres.
Hvordan beregner jeg teststørrelsen?Teststørrelsen bestemmes ved hjælp af formlen ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ).
Hvad sker der, hvis teststørrelsen er større end den kritiske værdi?Hvis teststørrelsen er større end den kritiske værdi, afvises nulhypotesen.
Hvad er signifikansniveauets rolle?Signifikansniveauet angiver, med hvilken sandsynlighed du er villig til at acceptere en fejl, hvis du forkert afviser nulhypotesen.


