Chi-kvadrat-tilpasningstest for normalfordeling med Excel

Kvadratet-Tilpasningstest er en simpel metode til at teste hypotesen om, hvorvidt en given datasæt følger en normalfordeling. I denne vejledning vil du lære, hvordan du udfører Chi-Quadrat-testen i Excel for at afgøre, om salget af smartphones følger en normalfordeling. Vi vil gå trin for trin gennem processen, lige fra oprettelsen af en frekvenstabel til beregning af teststørrelsen og sammenligning med den kritiske Chi-Kvadrat-værdi.

Vigtigste resultater

• Kvadratet-tilpasningstestet hjælper med at teste normalfordelinger.
• Det er vigtigt at oprette en frekvenstabel.
• Teststørrelsen sammenlignes med en kritisk værdi for at afvise eller acceptere nulhypotesen.

Trin-for-trin vejledning

Trin 1: Forbered data

For at udføre Chi-Kvadrat-testen skal du først have dataene. Kopier salget af smartphones til en Excel-regneark. Sørg for, at dine data er organiseret i en enkelt kolonne.

Trin 2: Opret histogram

For at få de første visuelle indikationer om fordelingen, skal du oprette et histogram af dine data. Gå til "Indsæt" og vælg "Diagrammer". Tilføj et histogram ved at vælge området for dataene.

Trin 3: Opret frekvenstabel

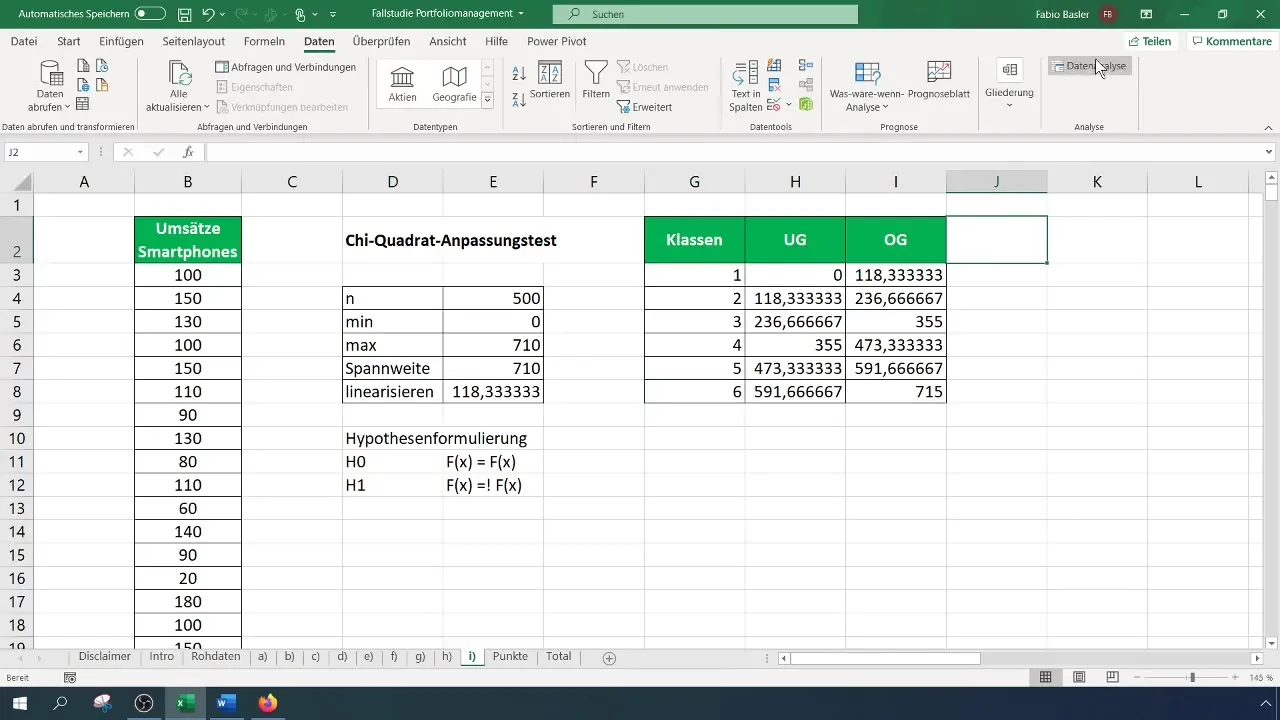
For Chi-Kvadrat-testen har du brug for en frekvenstabel. Bestem først antallet af klasser til din tabel - i dette tilfælde bruger vi seks klasser. Beregn intervalbredden og opret tabellen derefter.

Trin 4: Beregn frekvenser

Nu skal du beregne de observerede frekvenser for hver klasse. Gå til "Dataanalyse" i menuen og vælg "Histogram". Vælg inputområdet for dine data og klassetærsklerne. Bestem outputområdet for frekvenstabellen.

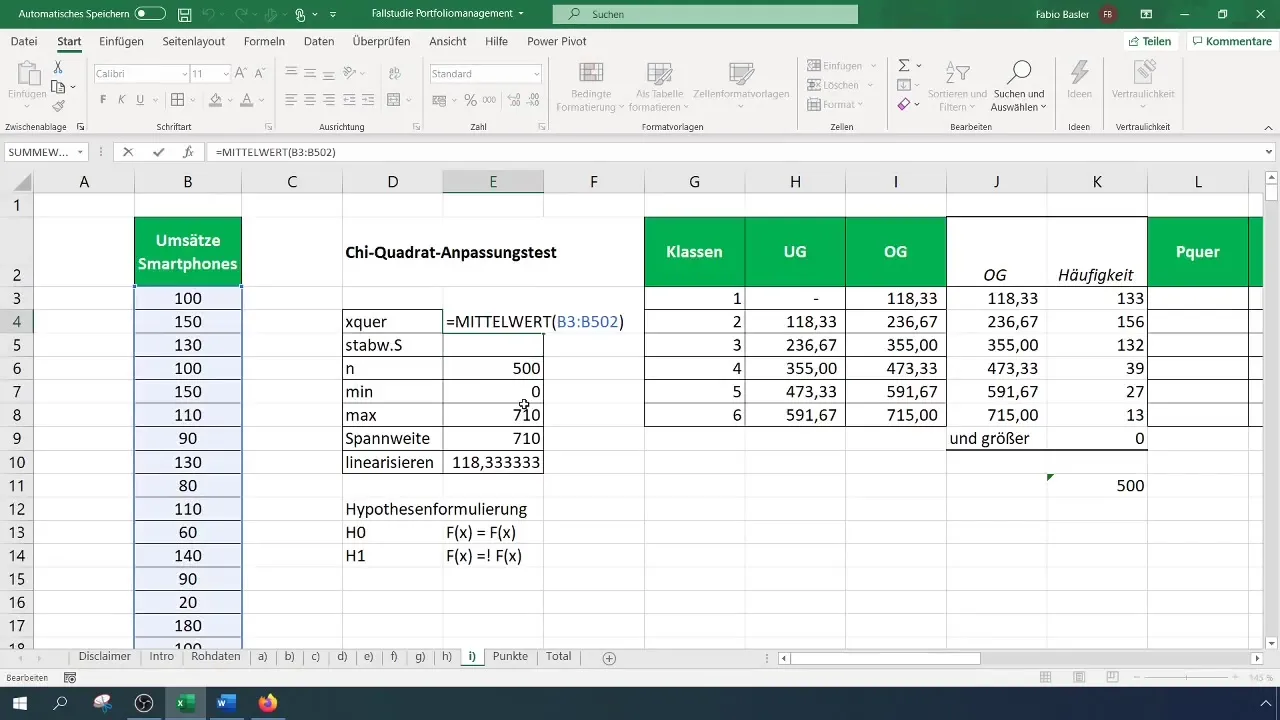
Trin 5: Beregn forventede frekvenser

For at finde de forventede frekvenser, skal du beregne sandsynlighederne for hver klasse baseret på antagelsen om normalfordeling. Du har brug for gennemsnittet og standardafvigelsen af dine data til dette.

Trin 6: Beregn teststørrelse

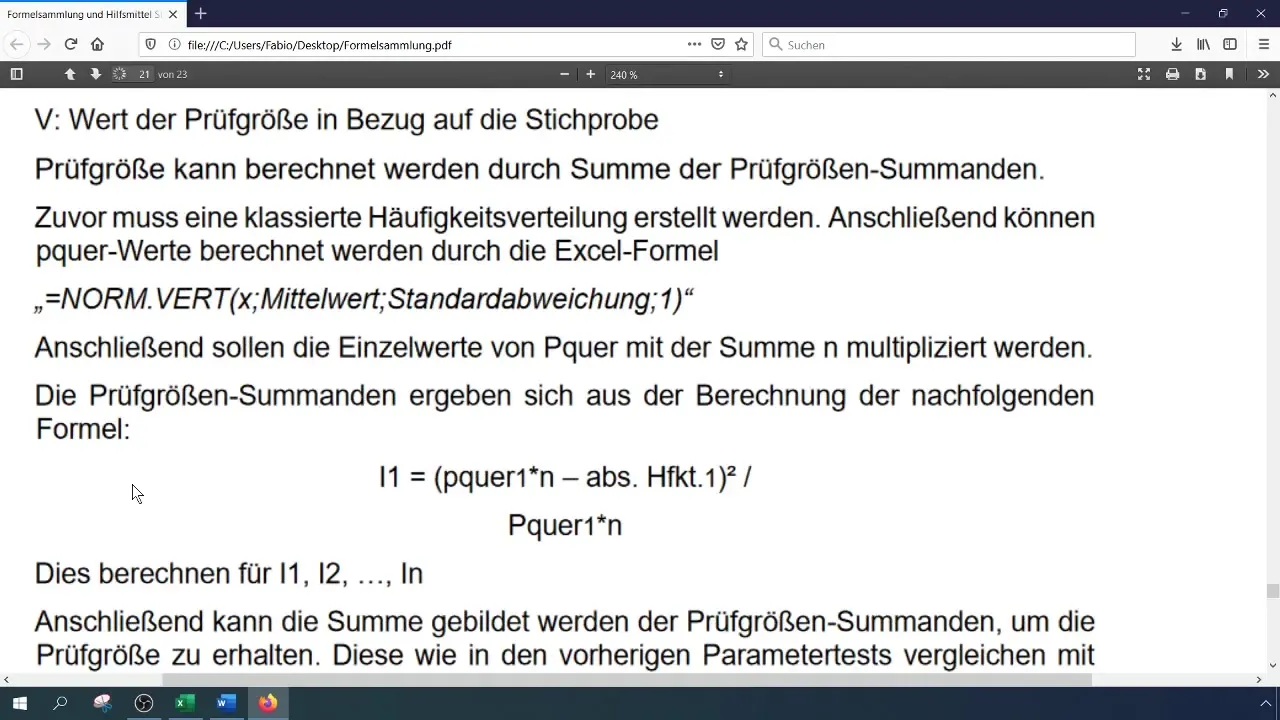
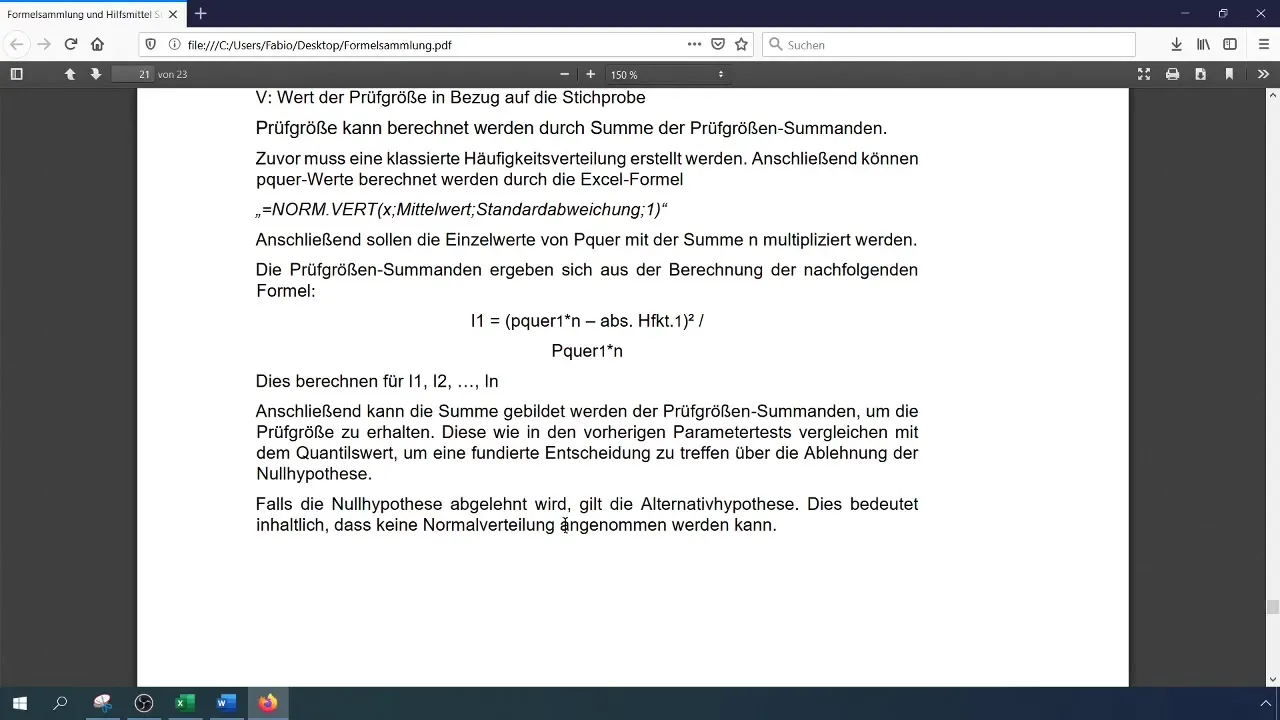
Beregn teststørrelsen (Chi-Kvadrat) med formlen:

[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]

hvor (O_i) er de observerede og (E_i) er de forventede frekvenser. Du kan udføre denne beregning i Excel ved at gemme de enkelte komponenter i separate celler.

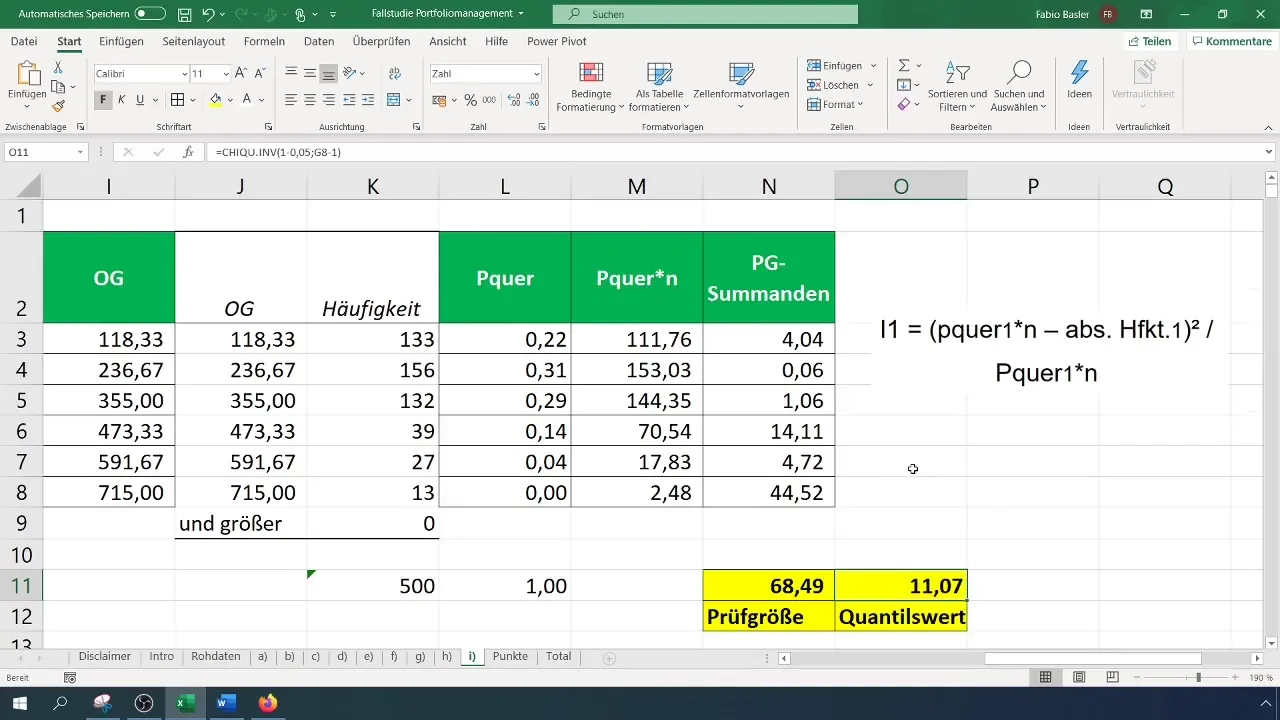
Trin 7: Beregn kritisk værdi

For at vurdere teststørrelsen skal du beregne den kritiske værdi ( \chi^2 ) for dit konfidensniveau og antallet af frihedsgrader. Antallet af frihedsgrader for Chi-Kvadrat-testen er (k - 1), hvor (k) er antallet af klasser.

Trin 8: Test af hypoteser

Sammenlign din beregnede teststørrelse med den kritiske værdi. Hvis teststørrelsen er større end den kritiske værdi, afvis nulhypotesen, hvilket betyder, at dataene ikke følger en normalfordeling. Ellers accepteres nulhypotesen.

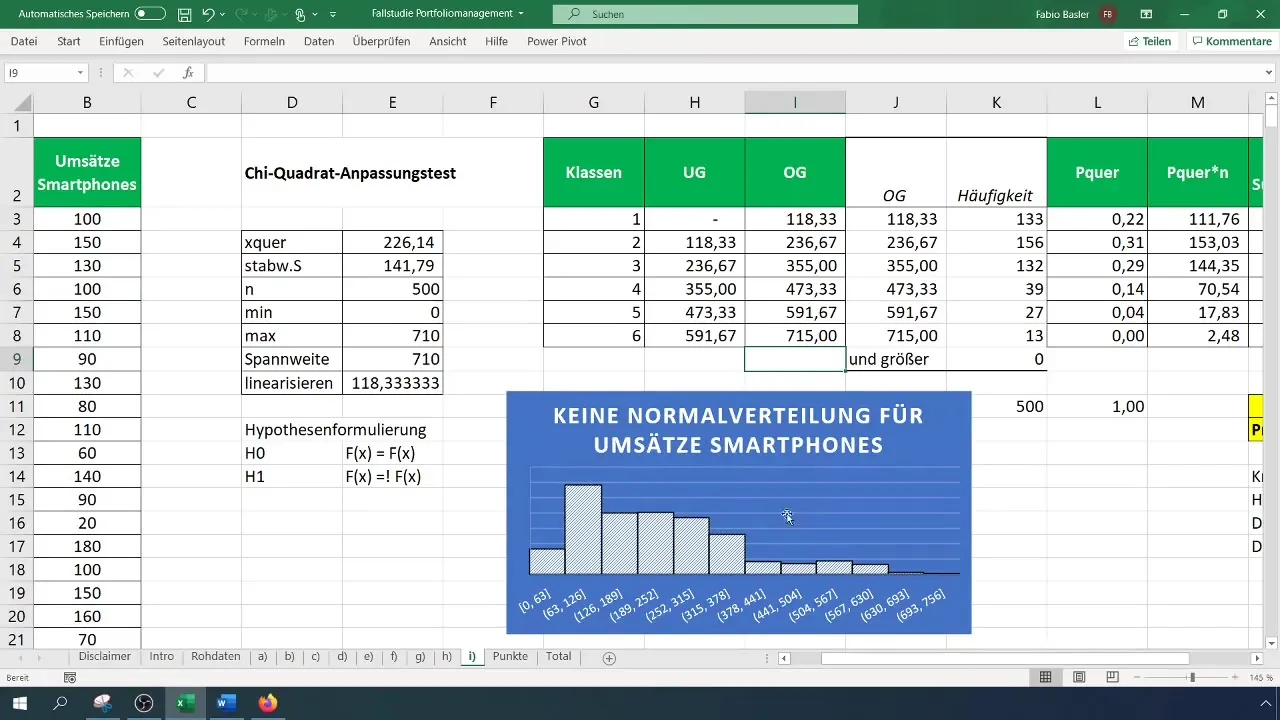
Trin 9: Opsummering af resultater

Hold styr på dine resultater og udvid dem med de grafiske data og hypotesetestene. Glem ikke at tjekke dit histogram for visuelt at bekræfte, at fordelingen ikke er normal.

Oversigt

I løbet af denne vejledning har du lært, hvordan du udfører chi-kvadrat-tilpasningstesten i Excel for at analysere normalfordelingen af dine smartphone-omsætninger. Trinnene inkluderer oprettelse af en klassificeret frekvenstabel, beregninger af forventede frekvenser, teststørrelsen og endelig sammenligning af disse med den kritiske værdi.