Evnen til at bruge dataanalyse-værktøjer i Excel er afgørende for succes på forretnings- og salgsområdet. Denne vejledning fokuserer på korrelations- og regressionsanalyse for at finde ud af, hvordan antallet af medarbejdere og antallet af telefonopkald påvirker omsætningstallene. Gennemførelsen af begge analyser hjælper dig med at vurdere disse relationer kvantitativt og gør fortolkningen af resultaterne forståelig.
Vigtigste opdagelser
- Forskellen mellem korrelation og regression: Korrelation viser sammenhængen mellem to variabler, mens regression undersøger virkningen af flere uafhængige variabler på en afhængig variabel.
- Indblik i den statistiske signifikans og kvalitet af modellen.
- Kvantitativ vurdering af vigtigheden af regressorerne.
Trin-for-trin vejledning
1. Forberedelser til dataanalysen
Inden du kan starte analysen, skal du sikre dig, at dine data er korrekt formateret i Excel. Importer dataene om omsætning, antal medarbejdere og telefonopkald til et Excel-regneark. Kontroller, at alle datasæt er komplette, og at de nødvendige variabler er til stede.

2. Gennemførelse af korrelationsanalysen
For at analysere korrelationen mellem variablerne omsætning, medarbejdere og telefonopkald, kan du beregne korrelationskoefficienten. Til dette skal du bruge formlen =KORREL() i Excel. For at få et overblik over alle variabler opretter du en korrelationsmatrix.
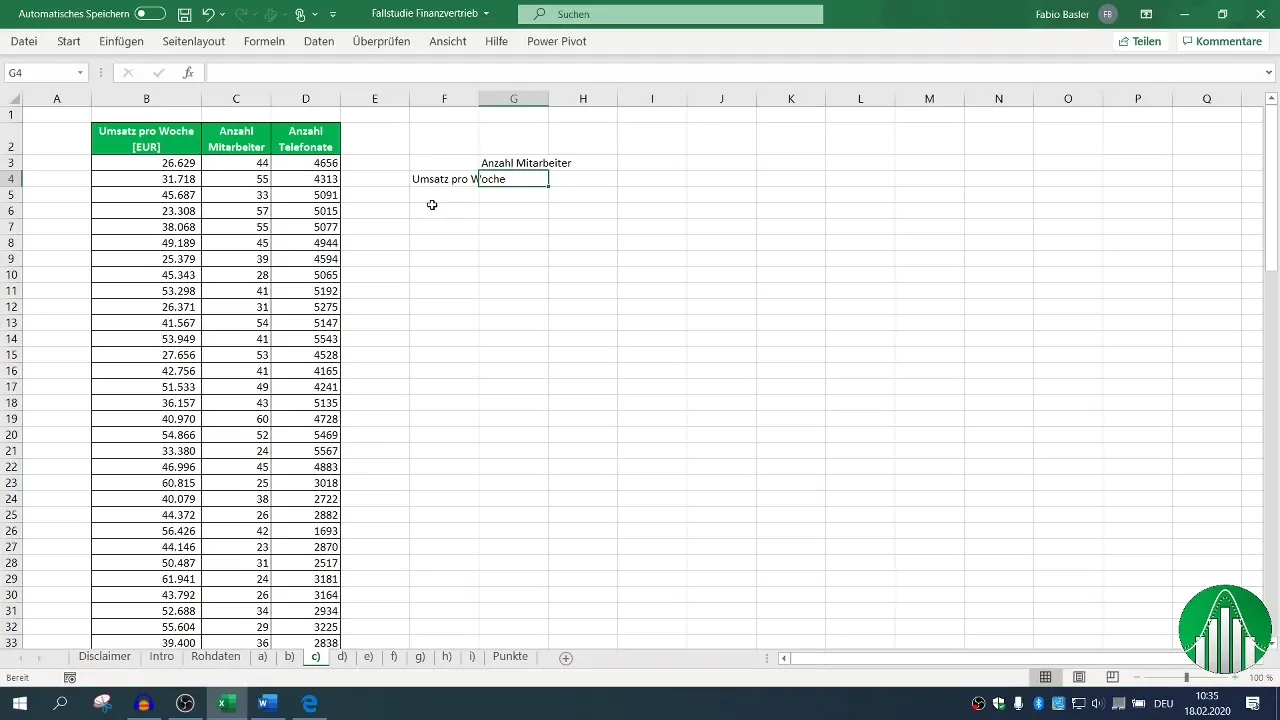
Først udvælger du de relevante kolonner for omsætning og antal medarbejdere. Ved hjælp af formlen =KORREL() markerer du områderne for omsætning og antal medarbejdere. Resultatet viser, hvor stærk sammenhængen er.
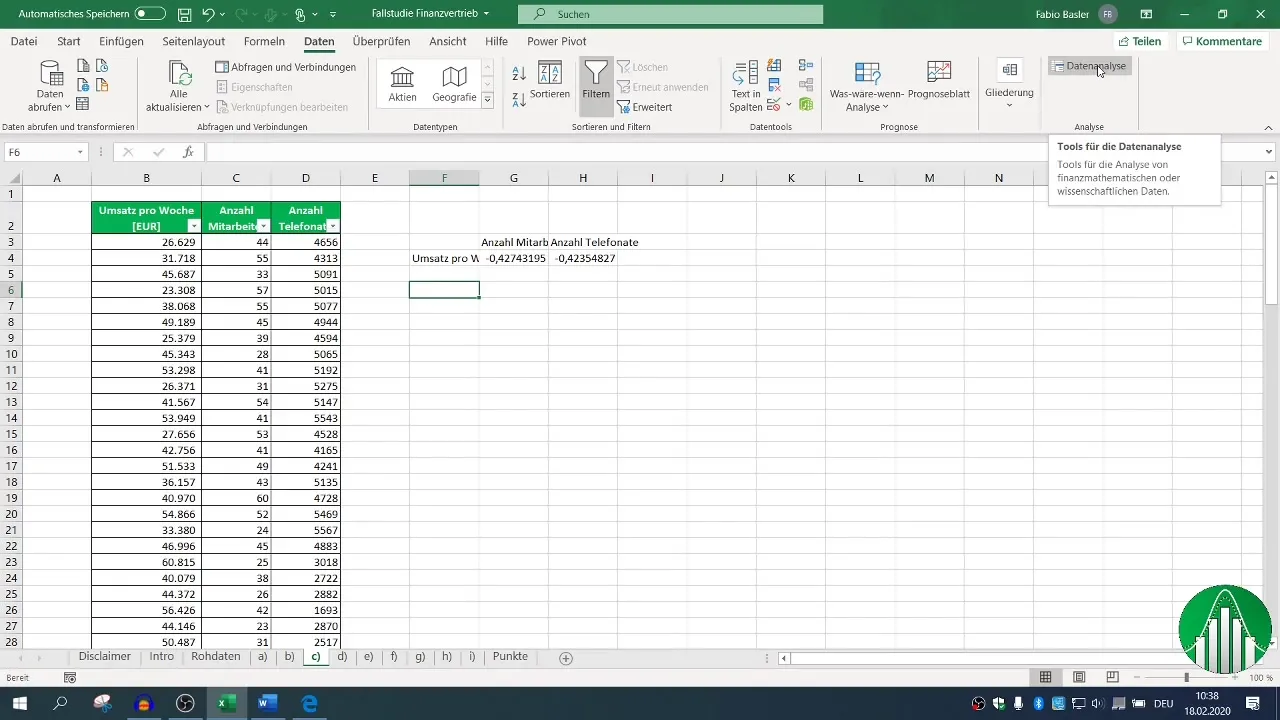
3. Oprettelse af en korrelationsmatrix
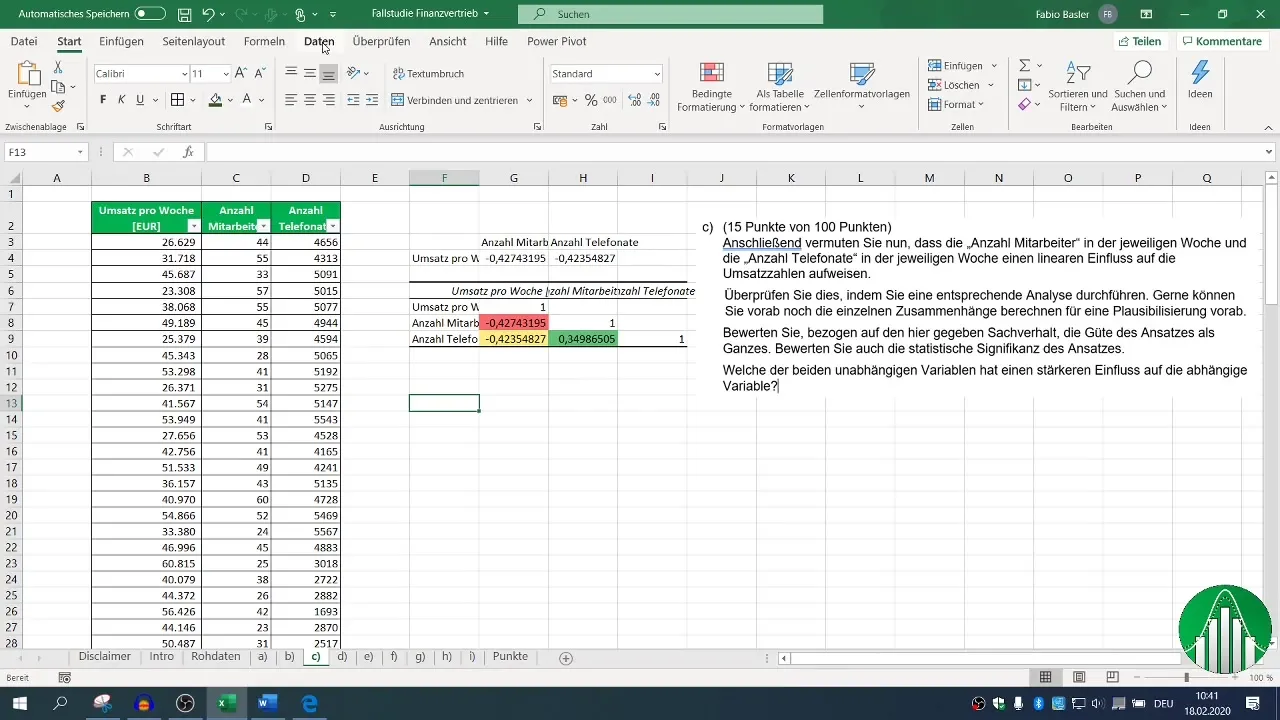
For en mere omfattende analyse anbefales det at bruge Excel's dataanalysefunktioner. Aktiver dataanalysefunktionen, hvis du endnu ikke har gjort det. Gå til fanen "Data", klik på "Dataanalyse" og vælg "Korrelation".
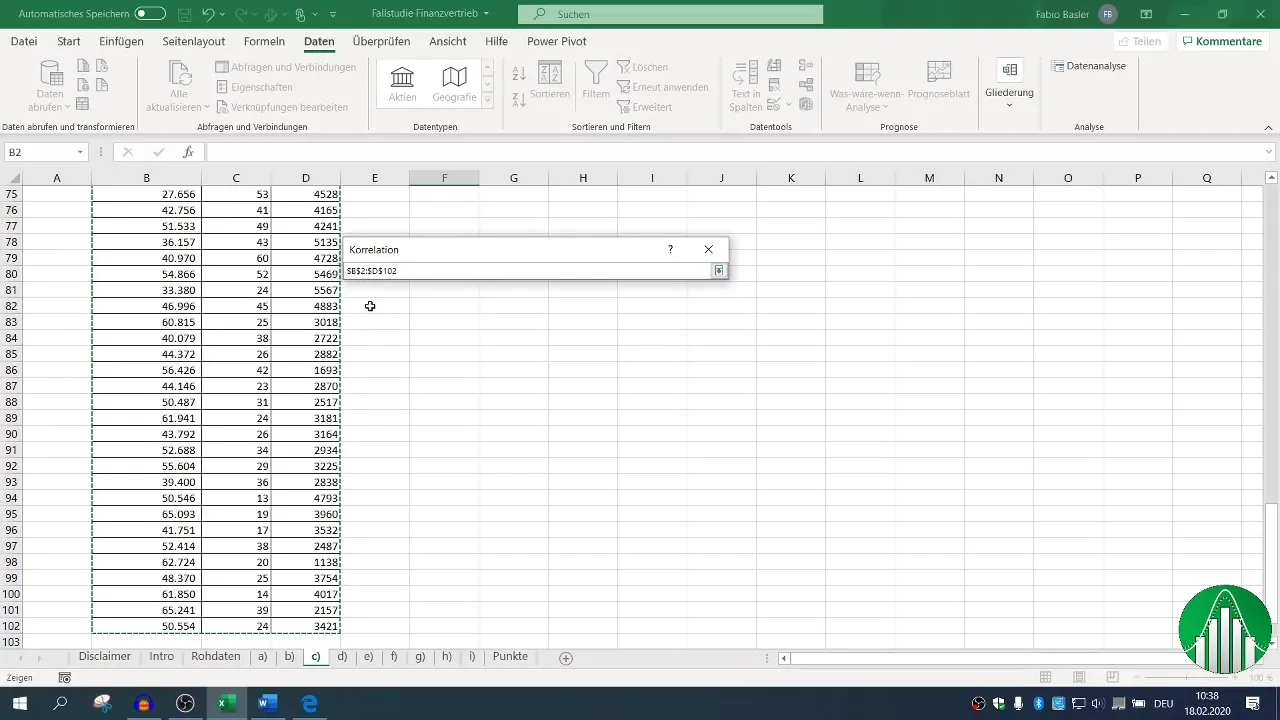
Definér inputområdet for dine data og sæt et flueben ud for overskriften for at lade Excel genkende betegnelserne korrekt. Når du har angivet outputområdet, kan du generere korrelationsmatricen, der viser alle relevante relationer.
4. Visualisering af korrelationerne
For at gøre resultaterne mere visuelle, kan det være hensigtsmæssigt at bruge en grafisk repræsentation ved hjælp af et XY-diagram. Vælg dine X- og Y-data og generer punktwolken.
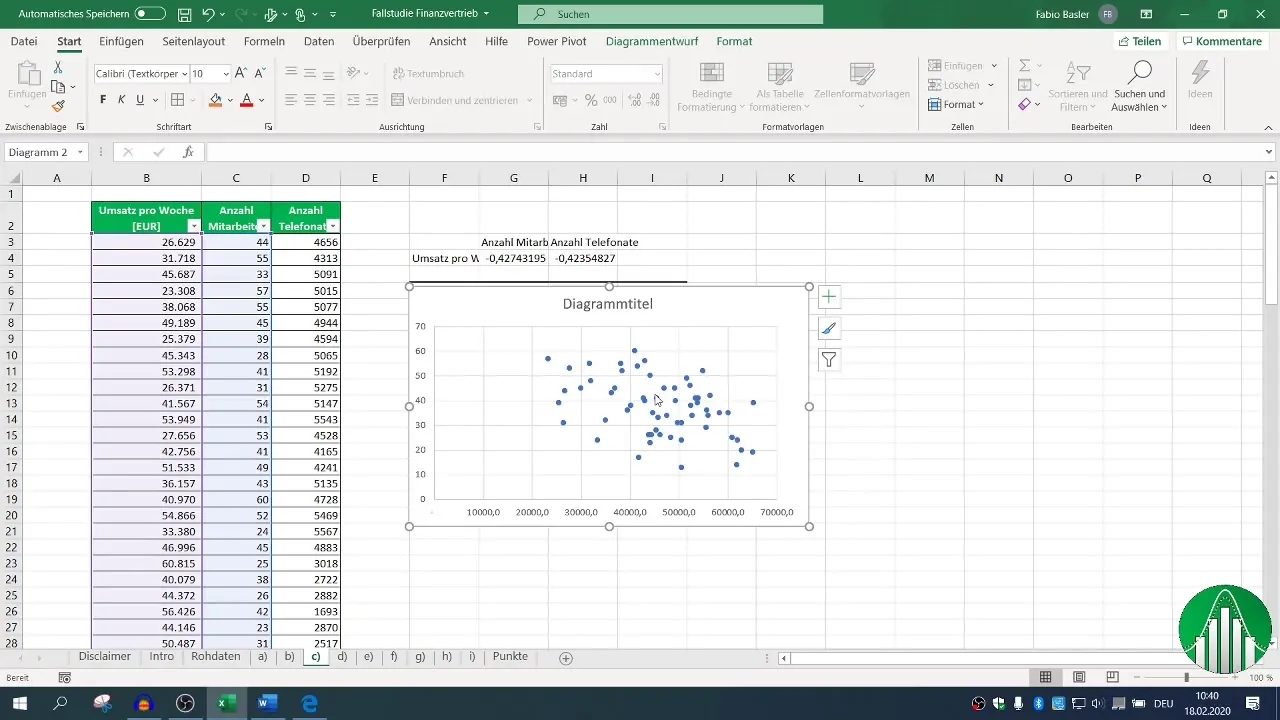
Tilføj en trendlinie for at visualisere sammenhængen. Dette kan give en mere intuitiv indsigt i dataene.
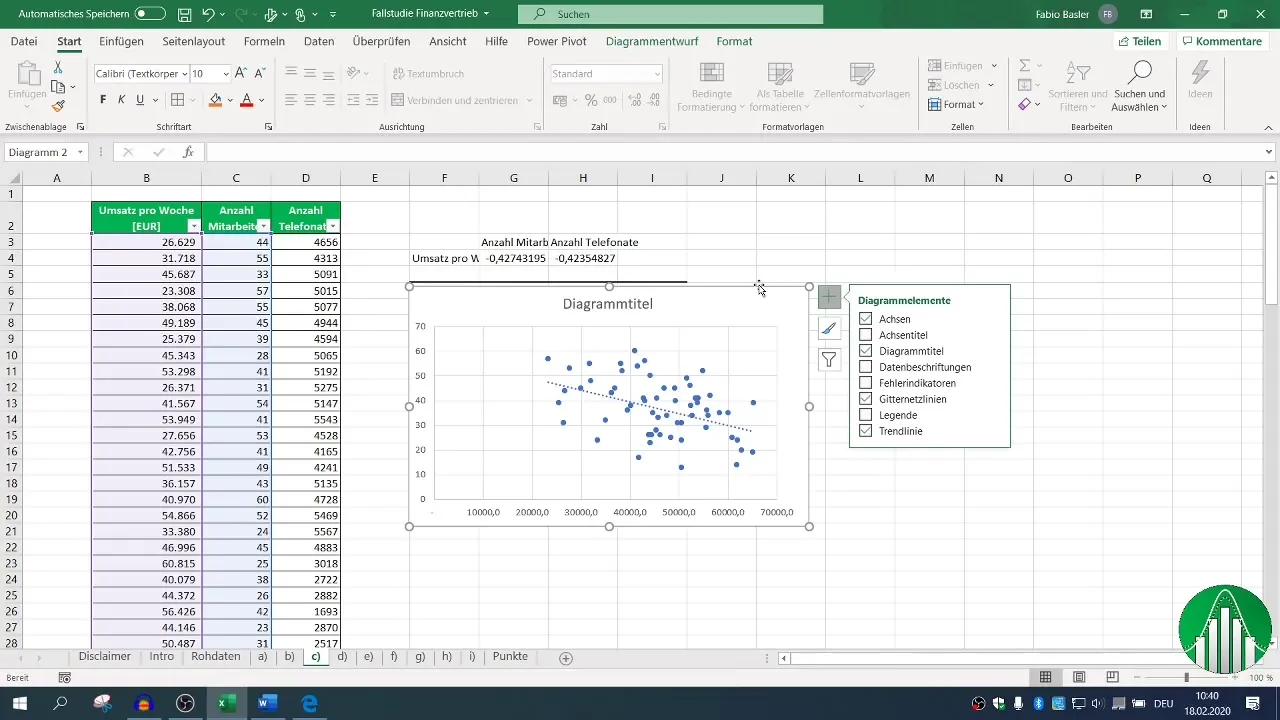
5. Udførelse af regressionsanalysen
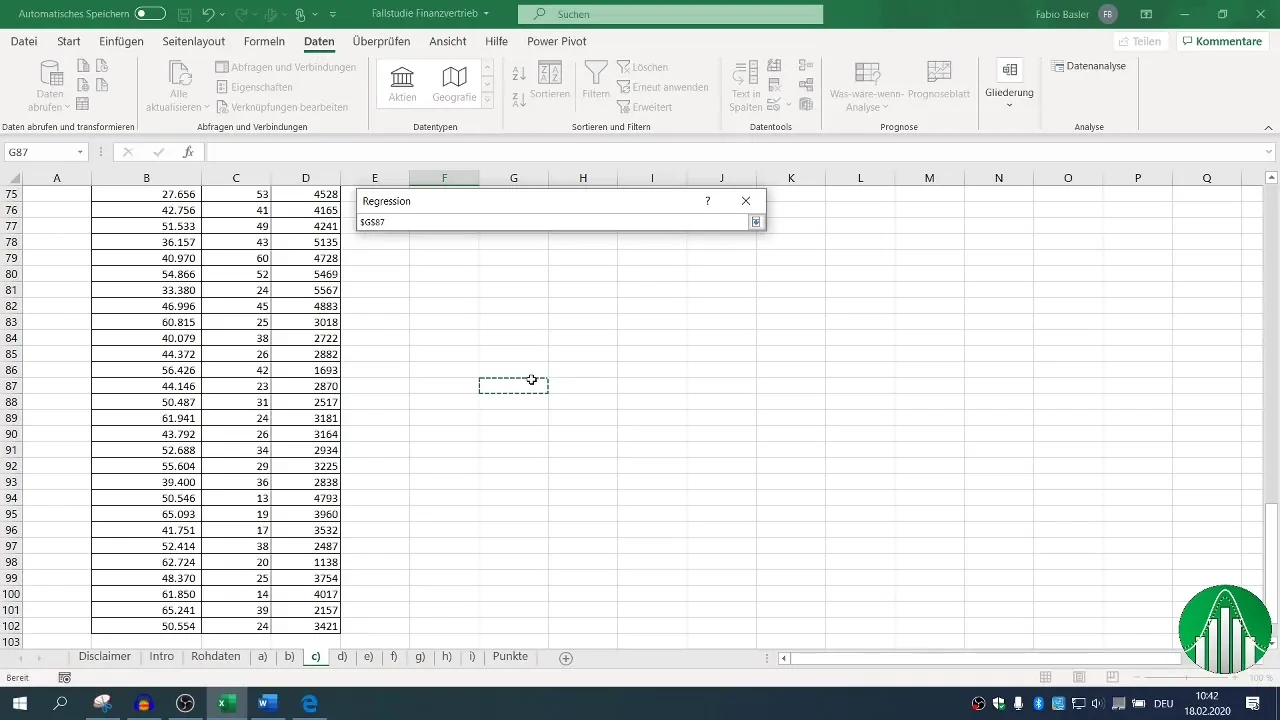
Nu kommer turen til regressionsanalysen. Gå igen til "Data" og vælg "Dataanalyse", derefter "Regression". Her skal du definere den afhængige variabel (omsætning) og de uafhængige variabler (antal medarbejdere og telefonopkald) for inputområdet.
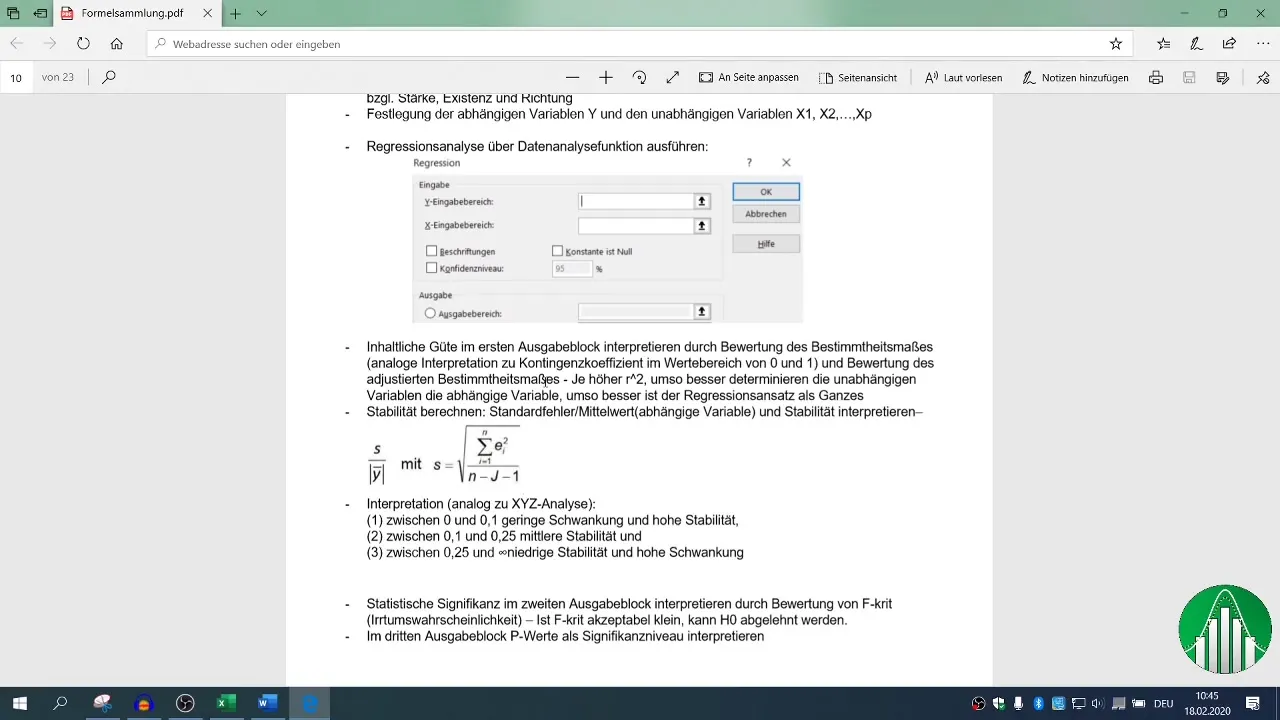
Sørg for, at overskriften for værdierne er sat, og definér dit outputområde. Standardtillidsniveauet er indstillet på 95 %, hvilket er tilstrækkeligt for de fleste analyser.
6. Evaluering af regressionsanalysen
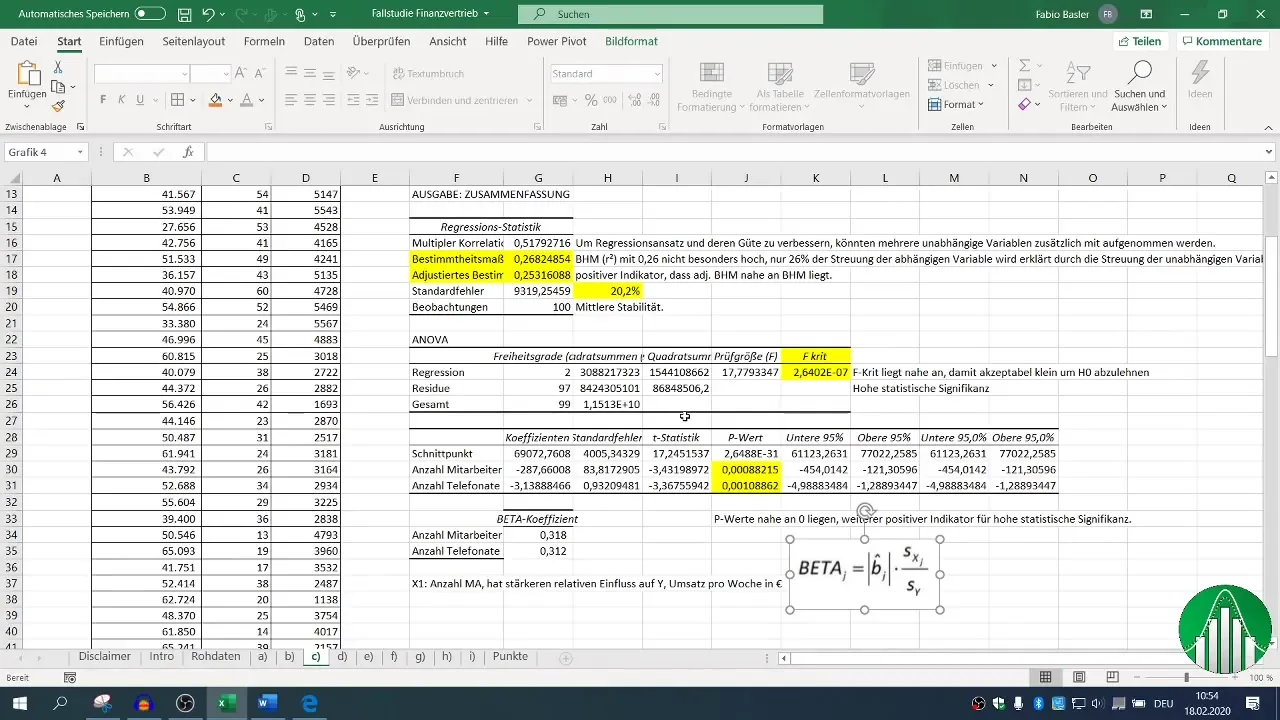
Når regressionen er gennemført, har du adgang til forskellige outputblokke. Fokuser på determinationskoefficienten (R²), som beskriver modellens kvalitet. En R² på 0,26 indikerer, at kun 26 % af omsætningens variabilitet forklares af de uafhængige variabler.
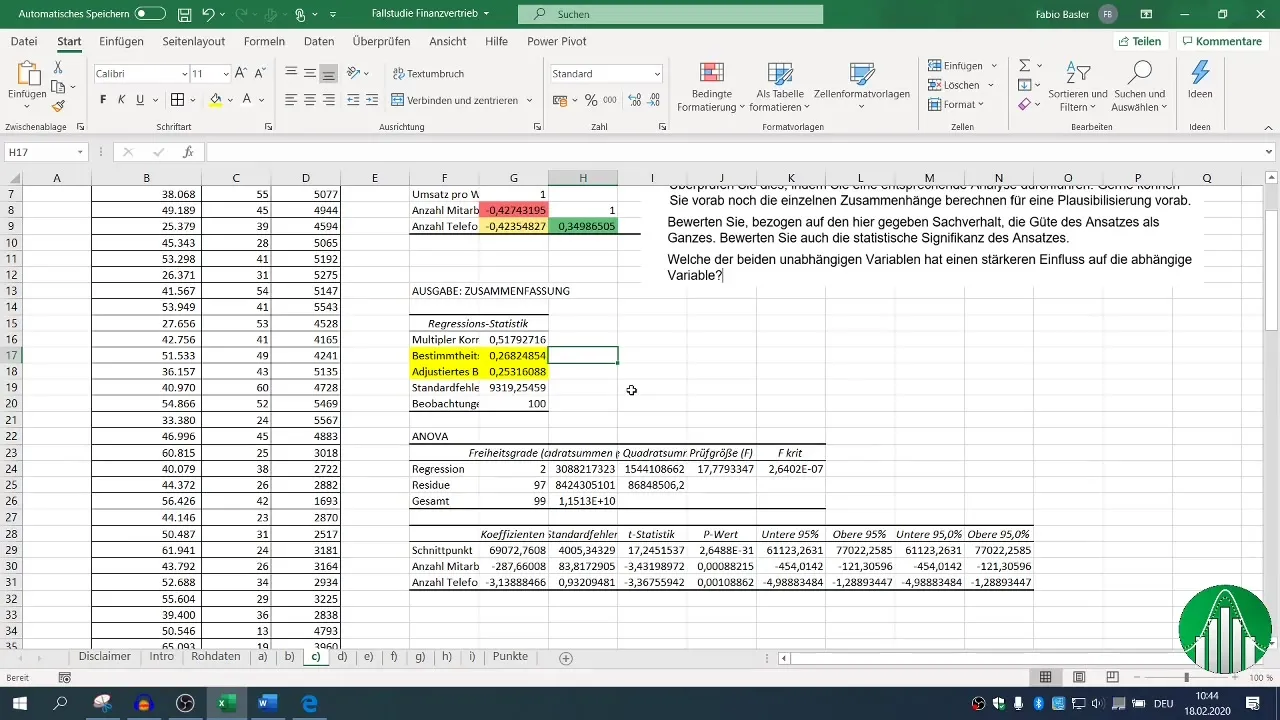
Justeret determinationskoefficient skal ligge tæt på R², hvilket i dette tilfælde er en positiv indikator.
7. Vurdering af statistisk signifikans
F-værdien og p-værdierne for de uafhængige variabler er afgørende for at vurdere din models statistiske signifikans. En p-værdi under 0,05 indikerer, at sammenhængen er statistisk signifikant.
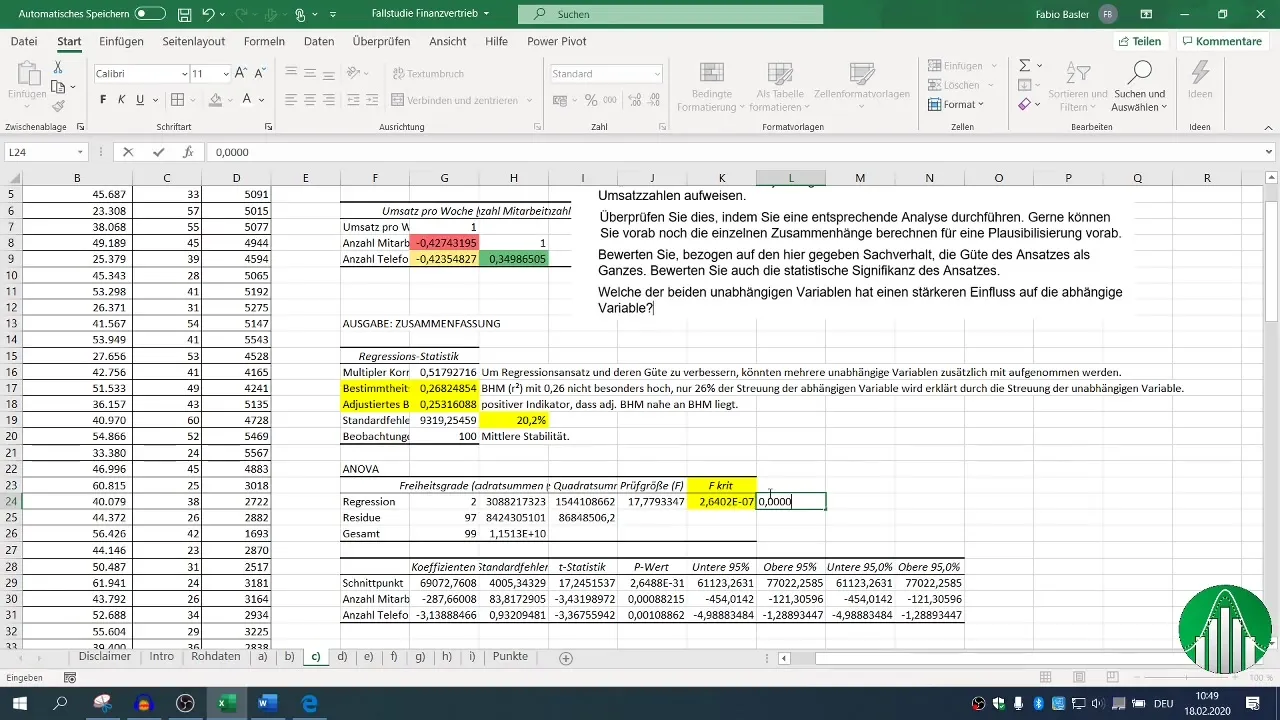
Vurdering af disse statistiske mål i forbindelse med R² hjælper dig med at forstå stabiliteten og validiteten af dine resultater.
8. Sammenligning af påvirkningsfaktorer
Endelig er du interesseret i at vide, hvilken faktor - antallet af medarbejdere eller antallet af telefonopkald - der har størst indflydelse på omsætningen. Her bruger du beta-koefficienterne og sammenligner dem.
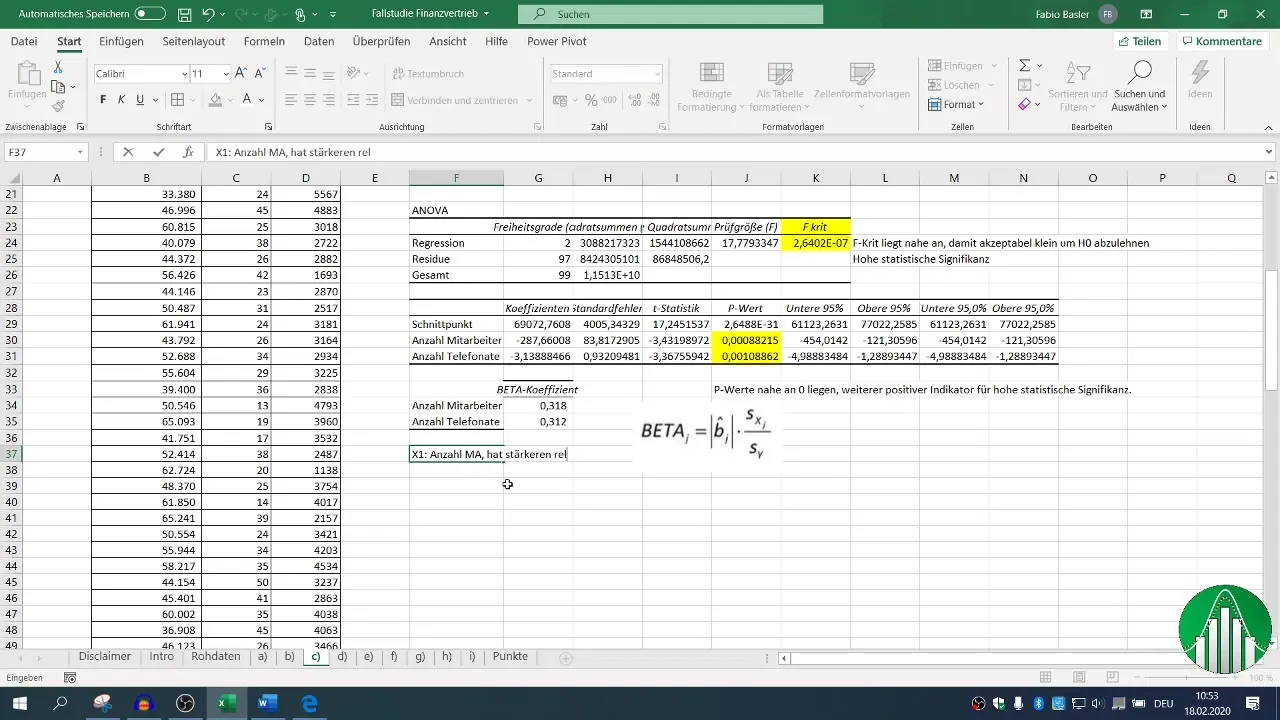
En højere beta-koefficient viser den relative indflydelse; det kan vise sig, at antallet af medarbejdere har større indflydelse på omsætningen end antallet af telefonopkald.
Opsummering
Den forrige analyse har givet dig værdifulde indblik i de statistiske relationer mellem variablerne omsætning, antal medarbejdere og telefonopkald. Ved systematisk udførelse af korrelations- og regressionsanalyser i Excel kan du træffe velbegrundede beslutninger baseret på dine resultater.
Ofte stillede spørgsmål
Hvorfor er en korrelationsanalyse vigtig?En korrelationsanalyse hjælper med at erkende sammenhængen mellem to variabler, før en detaljeret regressionsanalyse udføres.
Hvordan fortolkes R² i regressionsanalysen?En R² på 0,26 betyder, at 26 % af variationerne i den afhængige variabel (omsætning) kan forklares af de uafhængige variabler.
Hvad er forskellen mellem korrelation og regression?Korrelation måler sammenhængen mellem to variabler, mens regression vurderer virkningen af flere uafhængige variabler på en afhængig variabel.
Hvordan kan den statistiske signifikans testes?Du tester den statistiske signifikans ud fra p-værdien; p-værdier under 0,05 betragtes som signifikante.
Hvilken rolle spiller beta-koefficienterne?Betakoefficienterne viser den relative indflydelse af de uafhængige variabler på den afhængige variabel.


