Normalfordeling i Excel - Beregn sandsynligheder let

Normalfordelingen er et centralt begreb inden for sandsynlighedsteori og statistik. I enhver dataindsamling, der er jævnt fordelt, observerer vi den såkaldte klokkekurve, som ofte optræder i undersøgelser og salgsanalyser. I denne vejledning vil du lære, hvordan du med Excel beregner og visualiserer normalfordelingen for en undersøgelse for at bestemme afgørende sandsynligheder. Med disse færdigheder kan du ikke kun forstå dine data bedre, men også bruge dem målrettet til at træffe velovervejede beslutninger.

Vigtigste erkendtgørelser

• Du lærer trin-for-trin beregningen af normalfordelingen i Excel.
• Mulighederne for grafisk præsentation af normalfordelingen bliver fremhævet.
• Du forstår, hvordan sandsynligheder for specifikke begivenheder kan beregnes.

Trin-for-trin vejledning

Først skal du sikre dig, at alle nødvendige data er klar i en Excel-tabel. Disse data repræsenterer for eksempel omsætningen fra en undersøgelse.

Visualisering af normalfordelingen

For at grafisk repræsentere omsætningens normalfordeling, følger du disse trin:

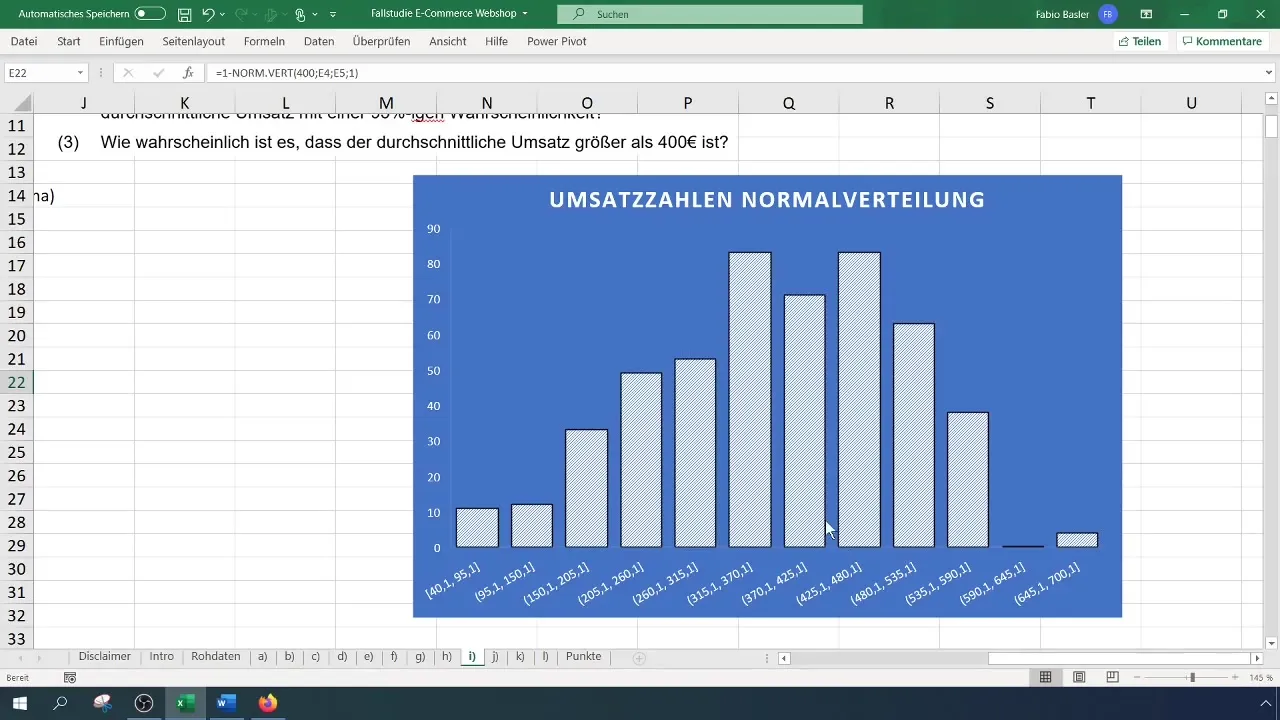
Først vælger du omsætningsdataene i din Excel-tabel og kopierer dem til en ny kolonne. I menulinjen klikker du på "Indsæt" og vælger "Diagram". Her vælger du et histogram for at illustrere fordelingen visuelt. Du kan vælge et tomt histogram for at vise standardværdierne for dine data.

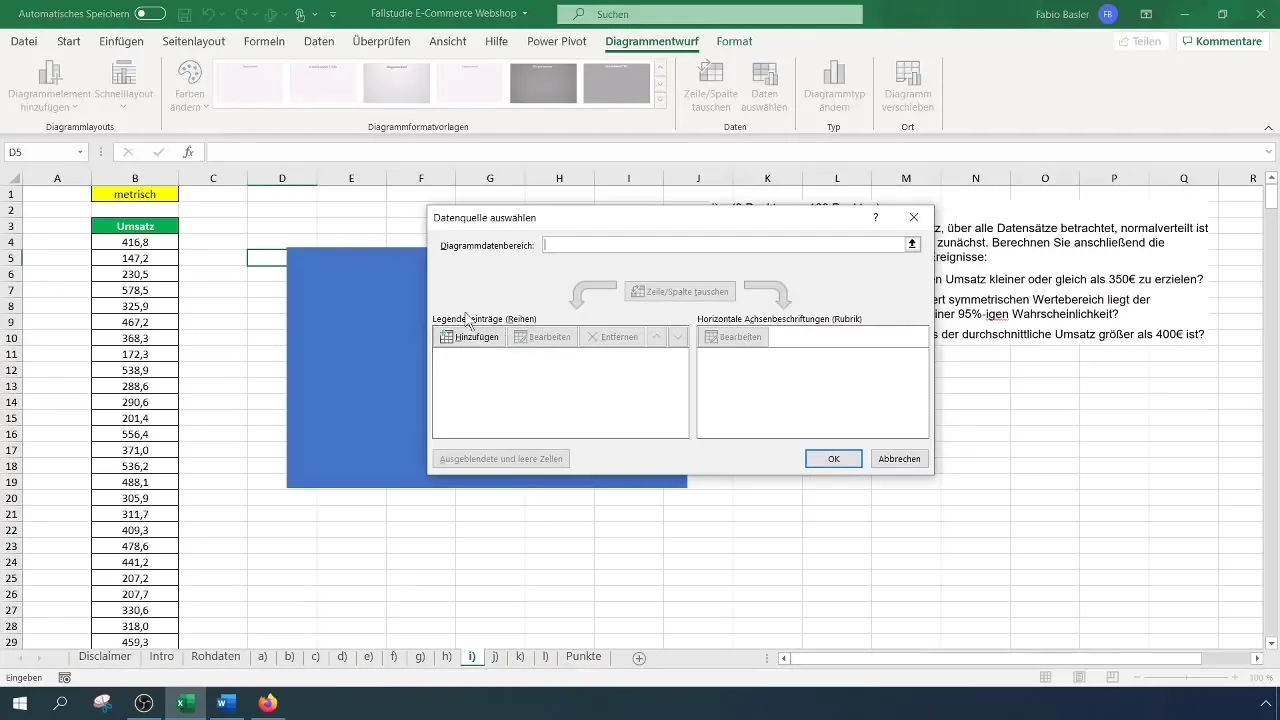
Højreklik på diagrammet og vælg "Vælg data". I det åbne vindue tilføjer du dine omsætningsdata som den første dataset. I rækkeværdierne vælger du alle datapunkter ved at holde Skift-tasten nede og vælge værdierne.

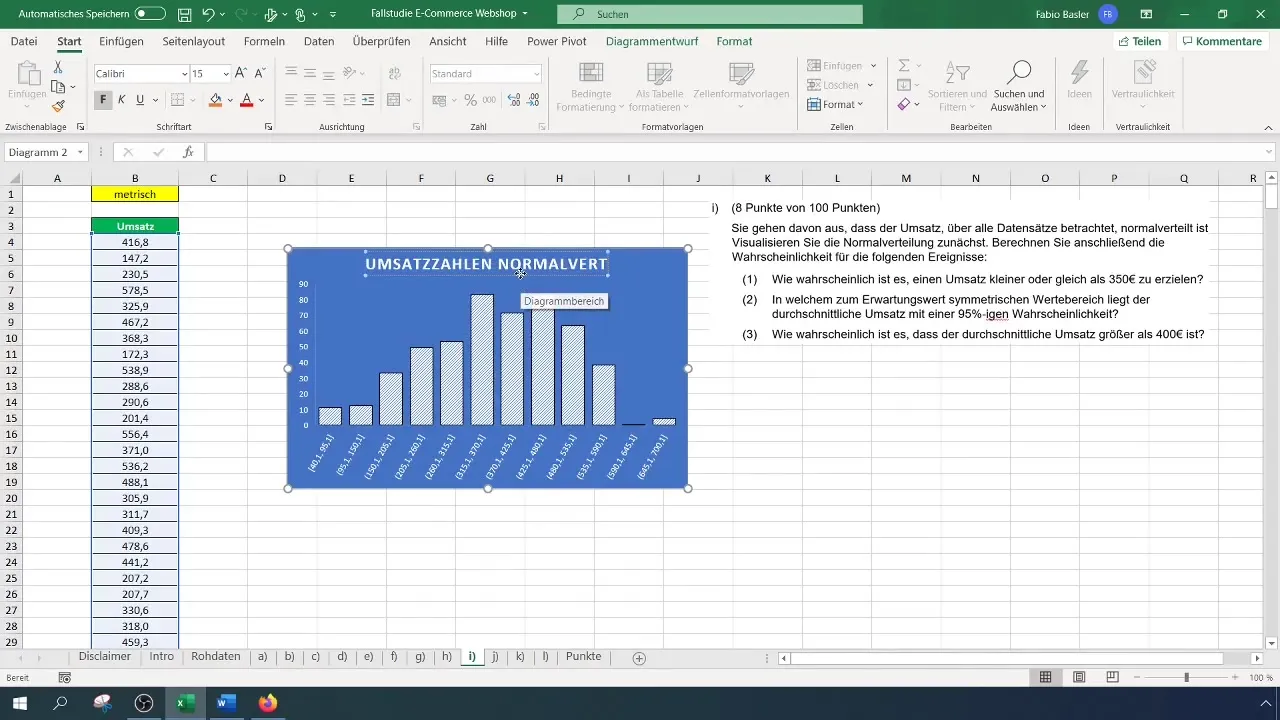
Når dataene vises i histogrammet, kan du tilpasse diagrammets titel for at gøre det mere repræsentativt. For eksempel kan du ændre titlen til "Omsætningsbeløb Normalfordeling". Sørg for, at klokkekurven er genkendelig; dette indikerer en normalfordeling.

Beregning af sandsynligheder

Næste opgave er at bestemme sandsynligheden for, at omsætningen er mindre end eller lig med 350 euro. For dette har du brug for gennemsnittet og standardafvigelsen af omsætningsdataene.

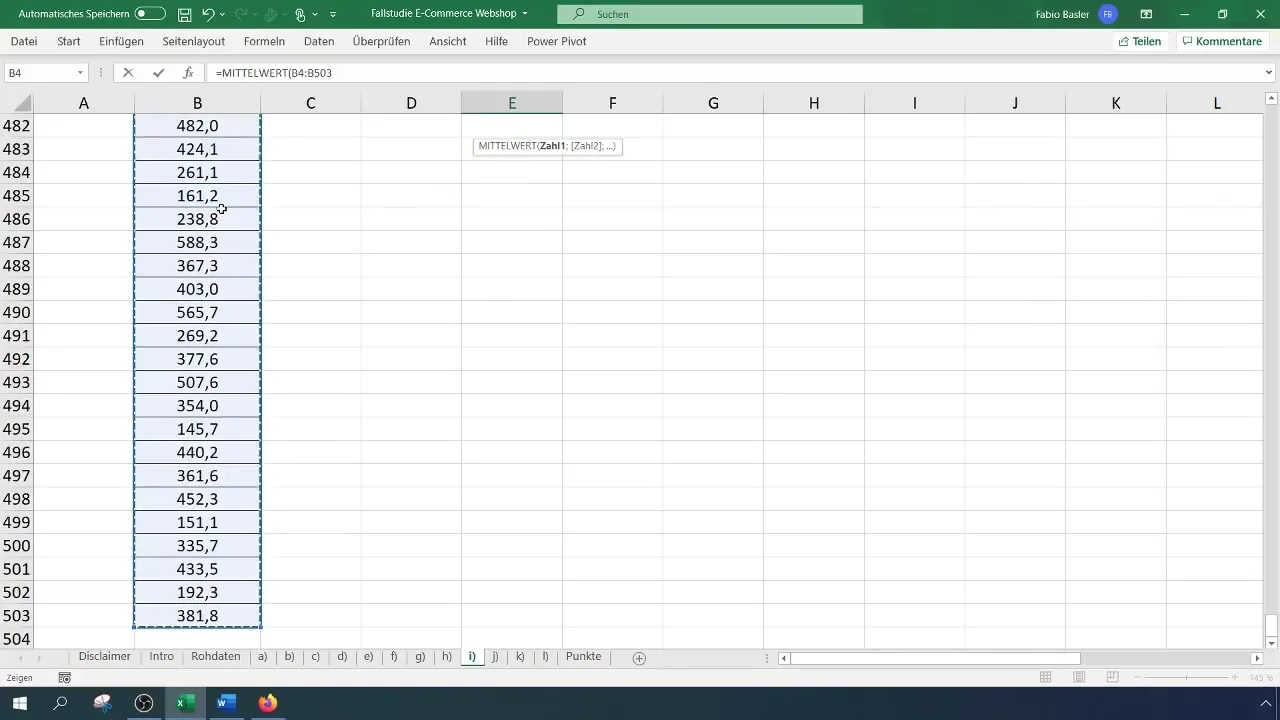
For at beregne gennemsnittet bruger du formlen =GNS(A1:A100) (Her skal A1:A100 erstattes med den faktiske dataområde). I dit eksempel kan dette resultere i en gennemsnitlig omsætning på 369 euro.

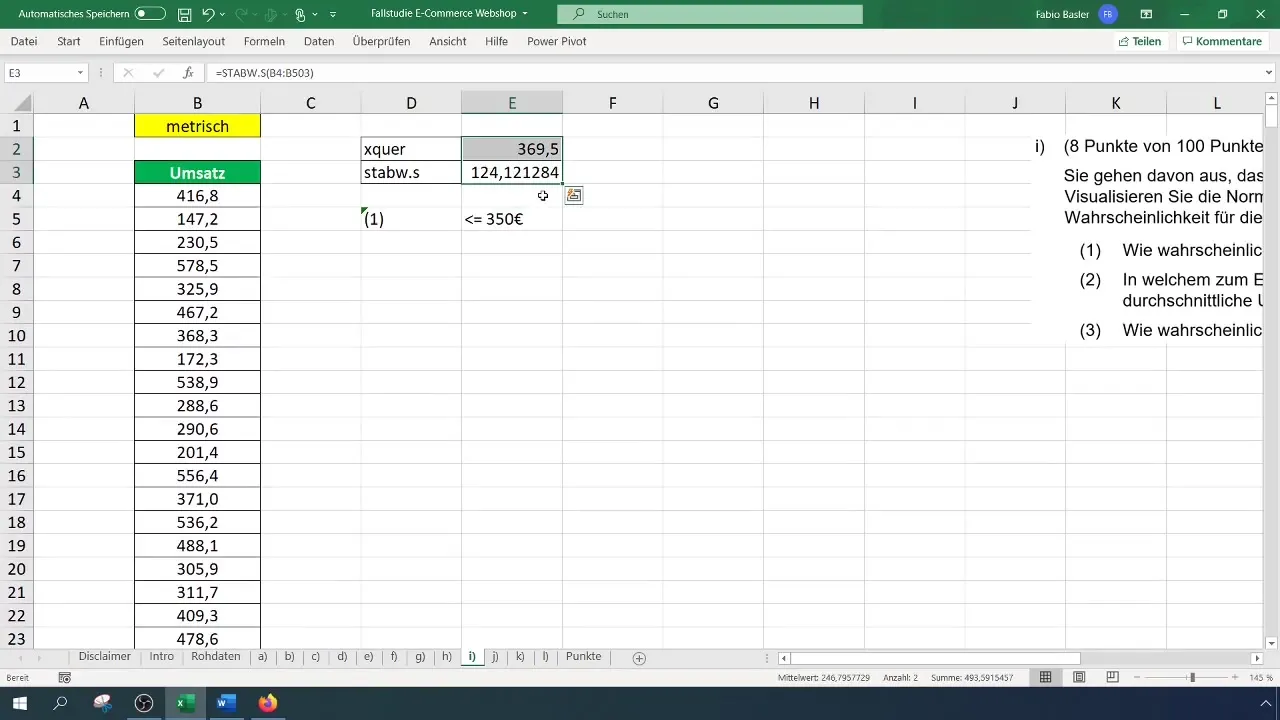
For standardafvigelsen bruger du formlen =STDAFV(A1:A100), og i dit tilfælde kan det være omkring 124,12 euro.

Nu kan du beregne sandsynligheden for en omsætning på 350 euro. Dette gøres ved formlen: =NORM.FORDEL(350; gennemsnit; standardafvigelse; SAND). Indsæt de relevante værdier og tryk Enter.

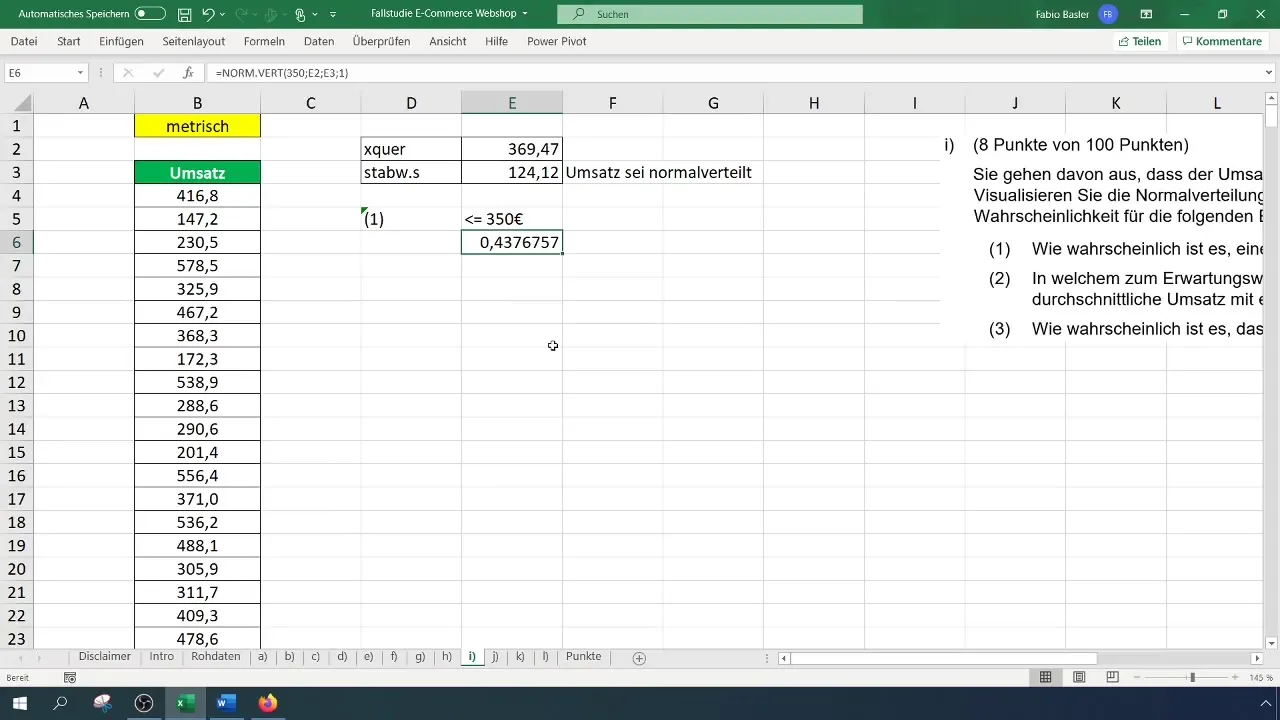
Resultatet af denne beregning kan vise dig, at sandsynligheden for at opnå en omsætning på mindre end eller lig med 350 euro er cirka 43,8 %. For at illustrere dette kan du formatere værdierne og ændre dem til procentvis visning.

Beregning af det symmetriske værdiområde omkring forventningsværdien

Næste mål er at bestemme det symmetriske værdiområde omkring forventningsværdien med en sandsynlighed på 95 %. Hertil skal du finde den kvantitative værdi for 95 %.

Dette gøres ved at indtaste formlen =NORM.INV(0,95) i en celle, hvilket giver dig kvantilverdien på 1,65.

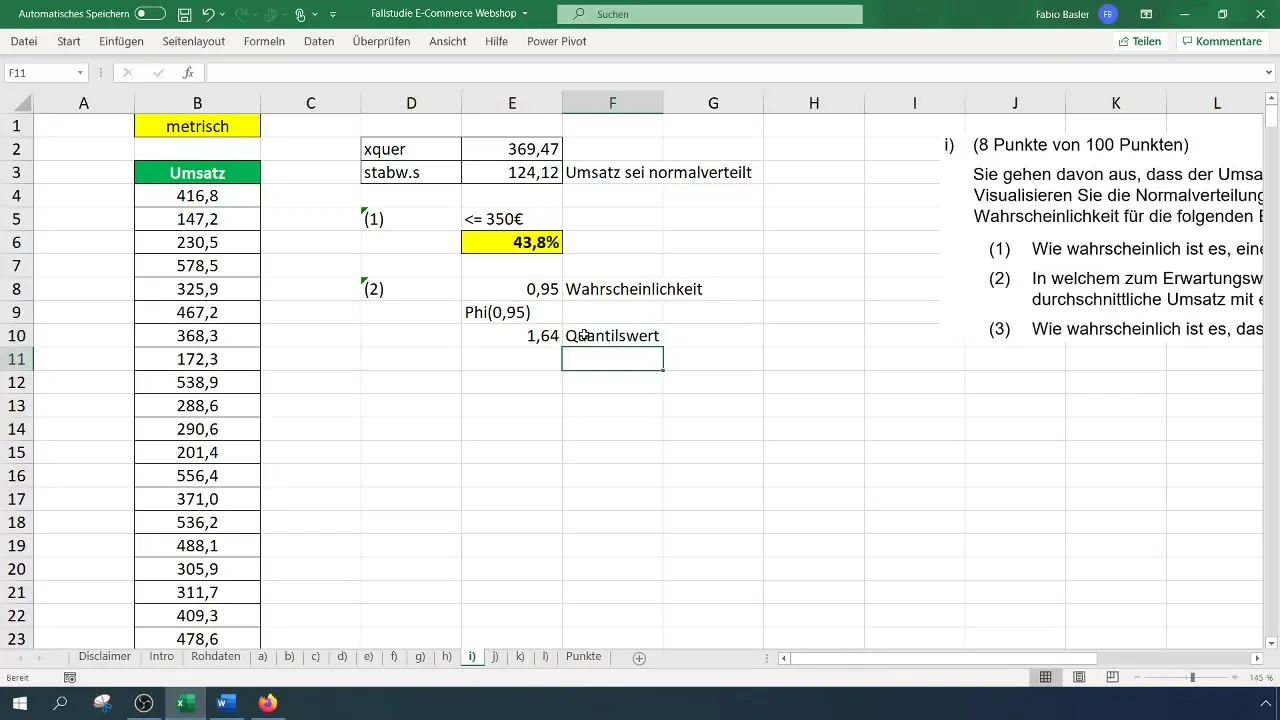
Derefter indsætter du denne beregning i en ligning for at finde værdiområdet. Formlen kan se sådan ud: Forventningsværdi + (Standardafvigelse * Kvantilverdi). Indsæt de relevante værdier og beregn det symmetriske værdiområde.

Hvis du for eksempel får en værdi på 572 euro, betyder det, at du med en sandsynlighed på 95 % kan forvente en omsætning inden for dette område.

Sandsynligheder for højere omsætning

I den sidste beregning vil du bestemme sandsynligheden for, at omsætningen er større end 400 euro. For dette skal du bruge formlen =1 - NORM.FORDELING(400; gennemsnit; standardafvigelse; SAND).

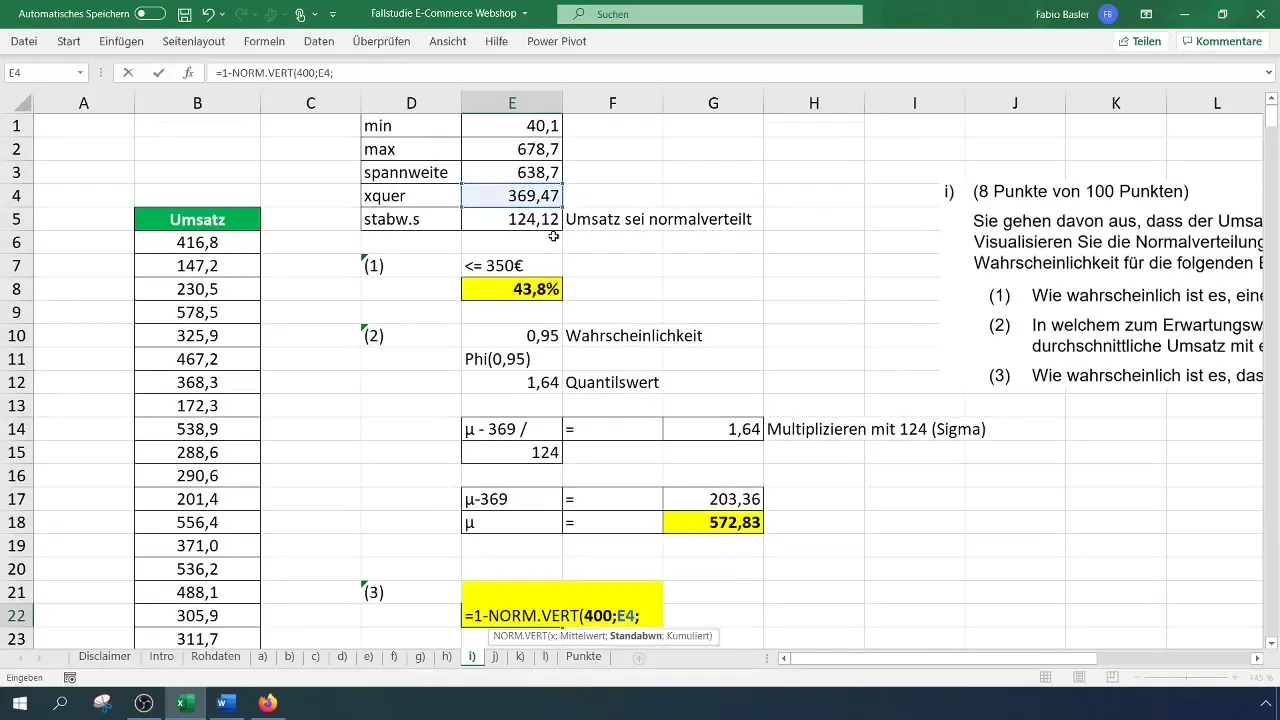
Sandsynligheden kan også her være på 40 %. Disse værdier er værd at undersøge. Når du ser på skalaen i histogrammet, kan du følge konsistensen af ​​procentdelen af de højere omsætninger.

Opsummering

I denne vejledning har du lært, hvordan du kan bruge Excel til at beregne sandsynligheder for normalfordelingen. Baseret på praktiske eksempler fra en undersøgelse har du lært, hvordan du kan arbejde med data både grafisk og beregningsmæssigt. Forståelsen af disse begreber vil hjælpe dig med at implementere statistiske analyser i dine projekter.