Beregningen af konfidensintervaller er en essentiel del af statistisk analyse, især når det handler om at drage konklusioner om en grundpopulation ud fra et udsnit. I denne vejledning viser jeg dig, hvordan du beregner et tosidet konfidensinterval for den gennemsnitlige omsætning af en undersøgelse i Excel. Du vil lære, hvilke forskellige trin der er nødvendige for at gå fra rådata til det endelige konfidensinterval og hvordan du implementerer denne metode i Excel.
Vigtigste erkendelser
- Et tosidet konfidensinterval angiver, inden for hvilke grænser den sande gennemsnitlige omsætning kan ligge med en bestemt tillidsgrad.
- For at beregne dette kræves gennemsnittet, standardafvigelsen, stikprøvestørrelsen og det tilhørende t-kvantil.
- Excel tilbyder de nødvendige funktioner til at beregne disse værdier og visualisere konfidensintervallet.
Trin-for-trin-vejledning
Trin 1: Forberedelse af data
Først bør du have de relevante data klar i Excel. For dette eksempel betragter vi kun normale kunder, da den gennemsnitlige omsætning kun skal beregnes for denne gruppe.

Du kan markere og kopiere dataene på dit regneark for at indsætte dem i et nyt område. Dette tjener til at filtrere din analyse efter de relevante kundegrupper.
Trin 2: Samling af grundlæggende information
Opret en simpel tabel i Excel, hvor du registrerer alle vigtige parametre. Det omfatter stikprøvestørrelsen (n), middelværdien (x̄), standardafvigelsen (σ) og den relevante kvantil. Vi ved allerede, at vi antager en normalfordeling og ikke har nogen tilgængelig varians.

Trin 3: Beregning af stikprøvestørrelsen (n)
For at finde antallet af observationer for normale kunder, skal du klippe de relevante data ud og finde antallet ved hjælp af FORMLEN =ANTAL(). I dette tilfælde bør du få 336 observationer fra de filtrerede data.
Trin 4: Beregning af middelværdien (x̄)
Beregn indtægternes gennemsnit ved at anvende formlen =GEMSNIT(). Dette giver dig den gennemsnitlige omsætning for normale kunder, som i vores eksempel er 362,80 euro.
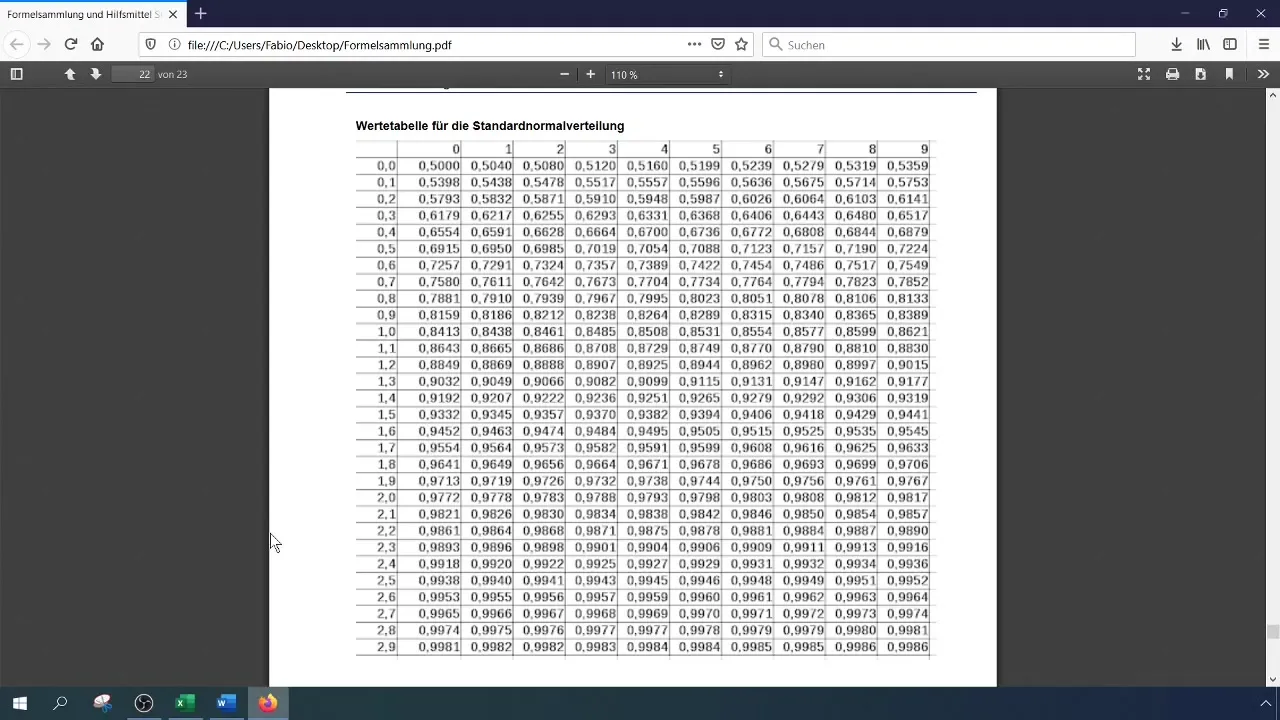
Trin 5: Bestem standardafvigelsen (σ)
Anvend formlen =STDAFV.S() for at beregne standardafvigelsen. Den vil være nødvendig for induktiv statistik, derfor bruger vi standardafvigelsen for stikprøven. Den beregnede værdi er 123 euro.
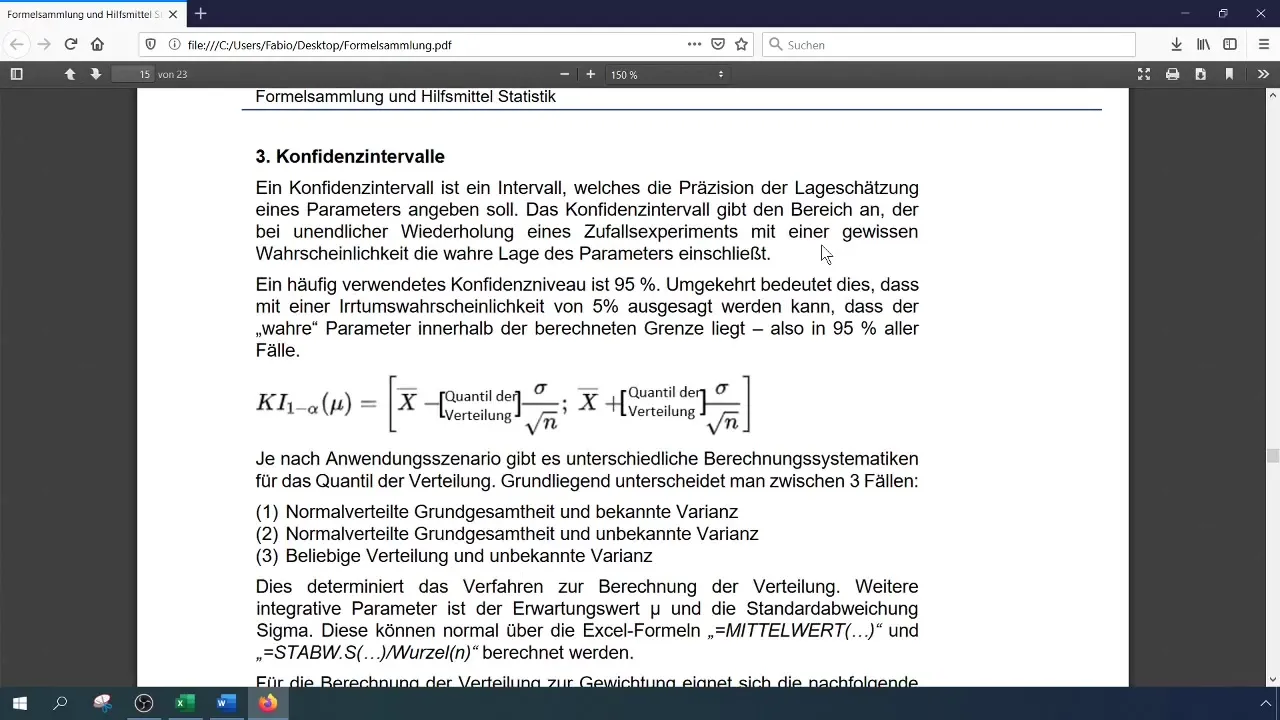
Trin 6: Beregn Sigma (σ / √n)
Nu beregner du standardafvigelsen for middelværdien ved at dividere standardafvigelsen med kvadratroden af stikprøvestørrelsen. Brug formlen: =Standardafvigelse/WURZEL(Stikprøvestørrelse).
Trin 7: Find t-kvantilen
Da vi har en normalfordeling med en ukendt varians, skal vi finde t-kvantilen. Brug Excel-funktionen =T.INV.2T() ved at angive alfa-niveauet (0,08) og frihedsgraderne (n-1). Dette giver dig i dit tilfælde en t-værdi på 1,8.
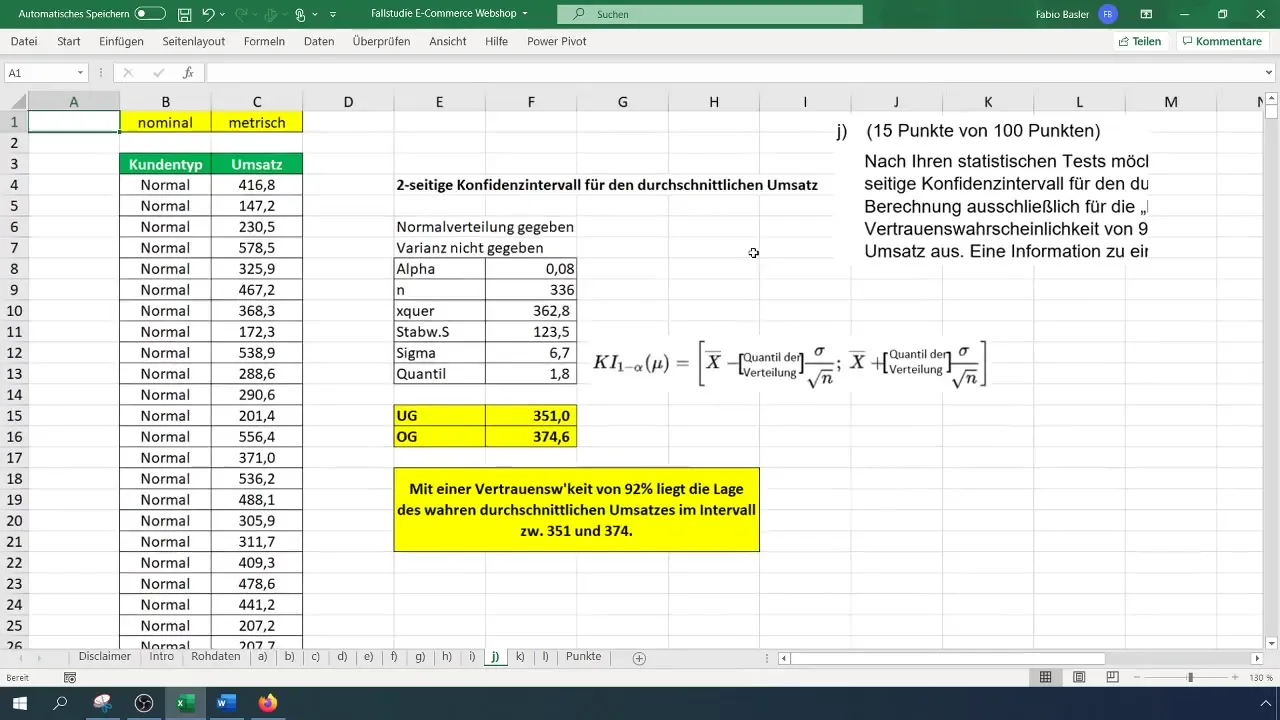
Trin 8: Beregn nedre grænse for konfidensintervallet
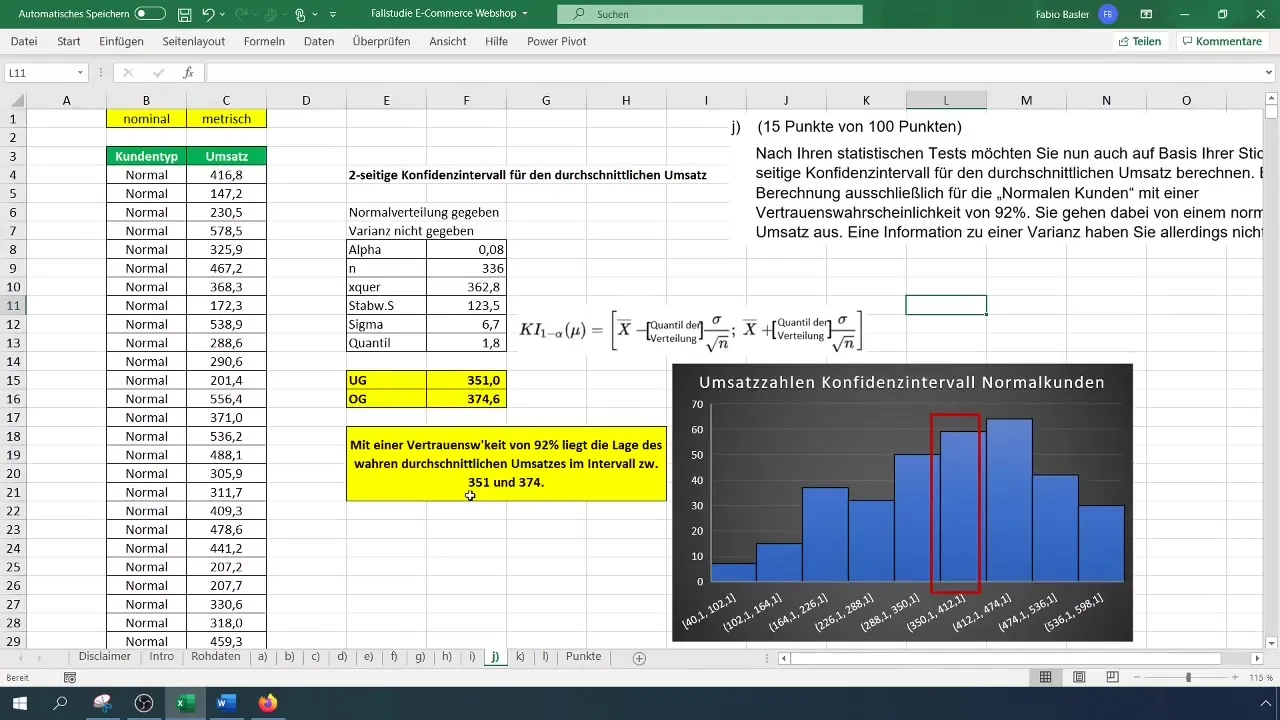
Beregn nu den nedre grænse for konfidensintervallet. Formlen er: =Middelværdi - (t-værdi * Sigma). Dette giver dig den nedre grænse, som i vores eksempel er 351 euro.
Trin 9: Beregn øvre grænse for konfidensintervallet
Nu kan du beregne den øvre grænse for konfidensintervallet. Formlen er lignende, dog lægger du denne gang t-værdien til din middelværdi: =Middelværdi + (t-værdi * Sigma). Den øvre grænse bliver dermed 374 euro.
Trin 10: Visualisering af konfidensintervallet
For at visualisere dine resultater kan du oprette et histogram i Excel og markere konfidensintervallet på det. Tegn en linje mellem den nedre og øvre grænse for at vise, i hvilket område den sande gennemsnitlige omsætning for normale kunder ligger med en tillidsgrad på 92 %.
Trin 11: Fortolkning og konklusion
Du kan nu konkludere, at med en tillidsgrad på 92% ligger den faktiske gennemsnitlige omsætning for almindelige kunder mellem 351 og 374 euro. Dette er vigtigt for yderligere beslutninger i din virksomhed.
Resumé
I denne vejledning har du lært, hvordan man beregner et tosidet konfidensinterval for gennemsnitlig omsætning i Excel. Du har gennemgået alle nødvendige trin, lige fra dataforberedelse til grafisk præsentation og fortolkning af resultaterne.


