Statistik ist ein wichtiges Werkzeug für Analysen in vielen Bereichen. Diese Anleitung zeigt dir, wie du die Rangkorrelationsanalyse nach Spearman in Excel durchführst. Mit dieser Methode kannst du den Zusammenhang zwischen ordinalen Variablen effizient quantifizieren. Wir betrachten dabei die Beziehung zwischen der Kundenzufriedenheit und der Marketingstufe.
Wichtigste Erkenntnisse
- Die Rangkorrelationsanalyse nach Spearman eignet sich besonders für ordinal skalierte Daten.
- Die Anwendung von Excel ermöglicht eine schnelle Berechnung und Visualisierung der Rangkorrelation.
- Ein schwacher positiver Zusammenhang zwischen Marketingstufen und Kundenzufriedenheit zeigt, dass mehr Investitionen in Marketing nicht zwangsläufig zu höherer Zufriedenheit führen.
Schritt-für-Schritt-Anleitung
Zunächst kommst du nicht umhin, die relevanten Daten einzufügen. Wir konzentrieren uns auf die Kundenzufriedenheit und die Marketingstufen. Diese Daten wurden im Rahmen einer Fallstudie erfasst.
Hierbei kannst du die Daten zunächst aus deinem Rohdatensatz kopieren und in einen neuen Arbeitsreiter einfügen. Beachte dabei, die Spaltenüberschriften klar zu definieren. Es könnte hilfreich sein, die Spalten als „Kundenzufriedenheit“ und „Marketingstufe“ zu benennen.
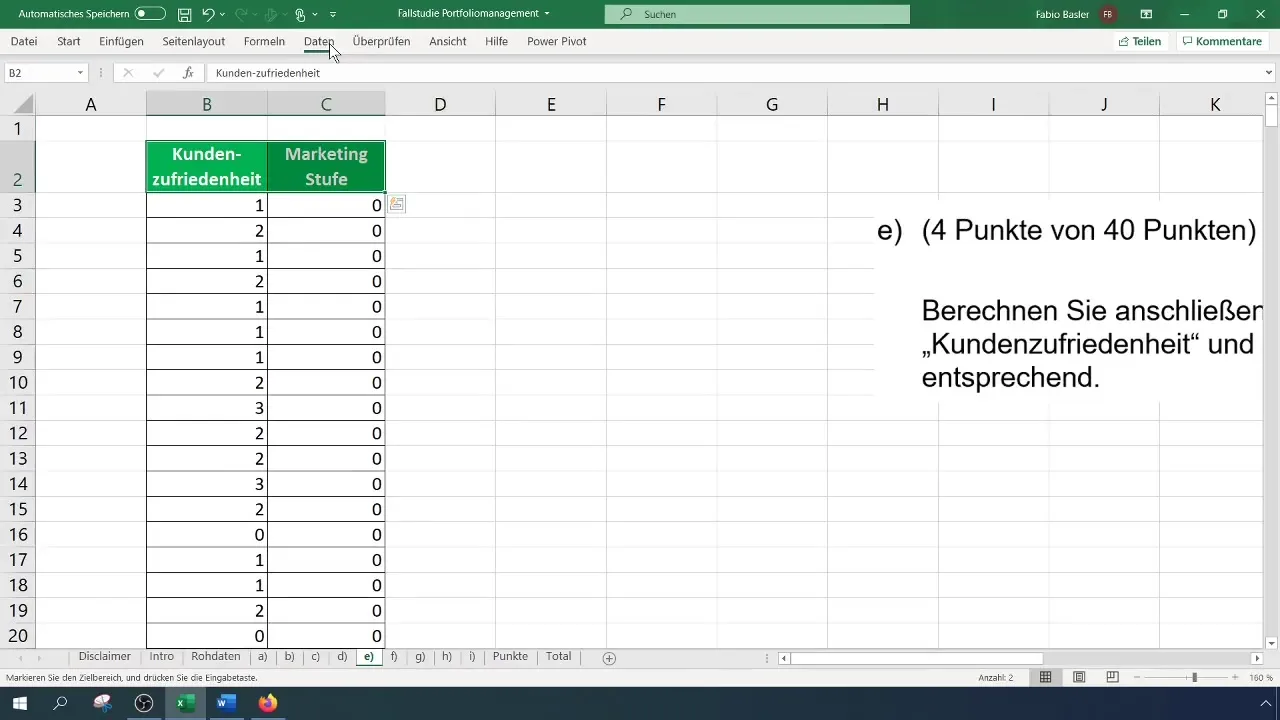
Nachdem du die Daten kopiert hast, ist es wichtig, die Skalenniveaus deiner Variablen zu überprüfen. Die Kundenzufriedenheit ist ordnal skaliert, während die Marketingstufen ebenfalls ordinal kategorisiert werden. Du solltest prüfen, ob du das korrekt verstanden hast, um einen Fehler bei der späteren Berechnung zu vermeiden.
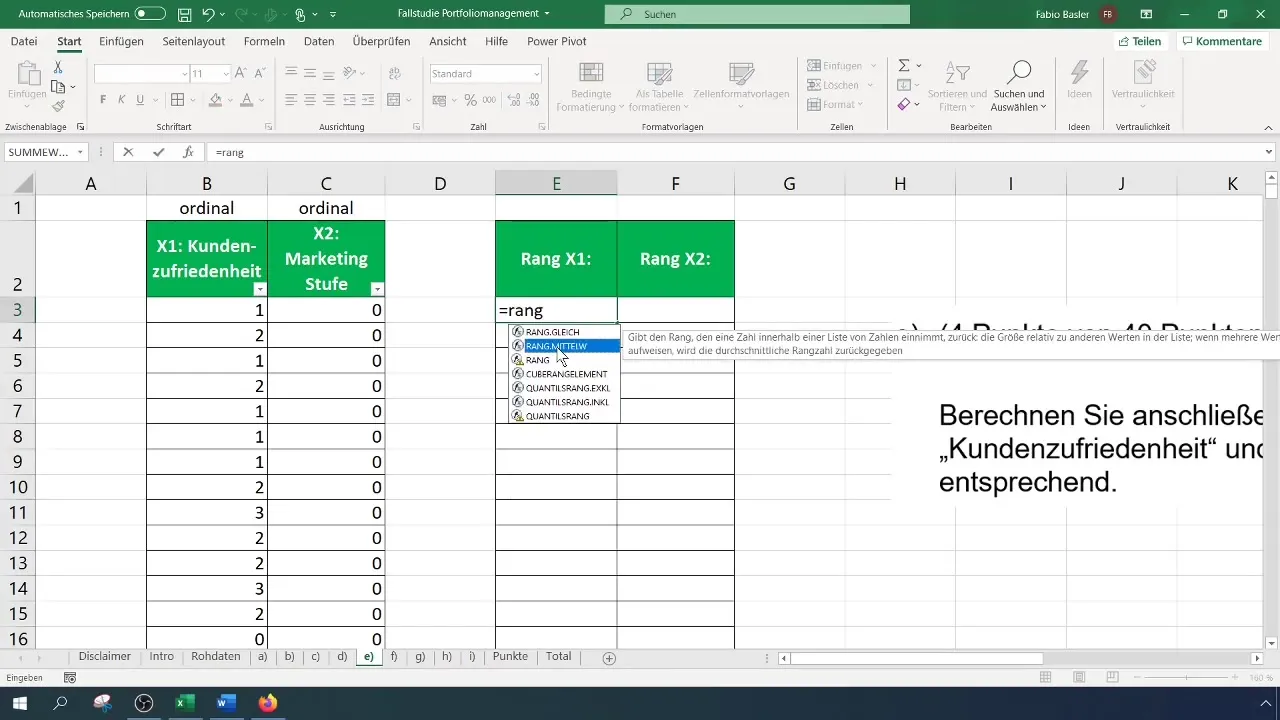
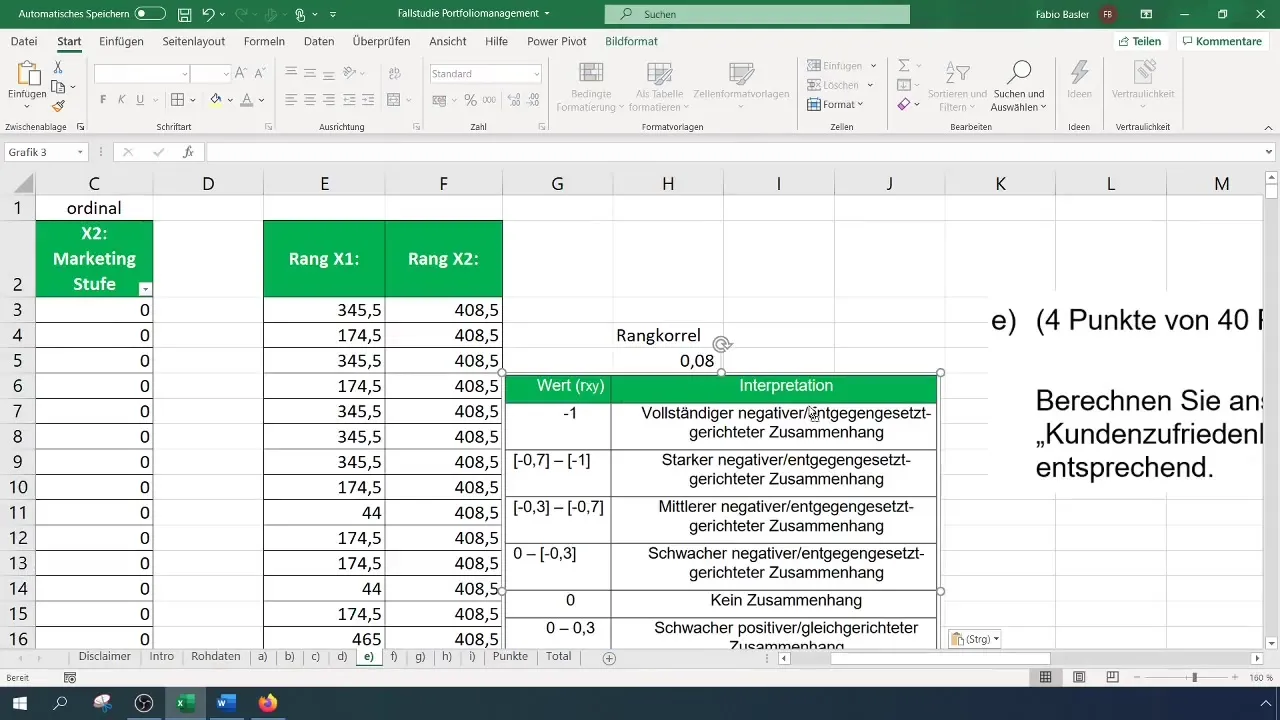
Als Nächstes bedarf es der Vorbereitung der Daten für die Rangkorrelationsanalyse. Du brauchst die Ränge der Variablen. In Excel funktioniert das über die Funktion „RANG.GLEICH“ oder „RANG.MITTEL.W“. Diese Funktion ordnet jeder Zahl in Bezug auf eine festgelegte Matrix einen Rang zu. Stelle sicher, dass du im richtigen Bereich arbeitest.
Um die Ränge für die Kundenzufriedenheit, die wir hier als Variable X1 bezeichnen, zu berechnen, wählst du zuerst die entsprechende Zelle aus. Für die erste Beobachtung bedeutet das, die Zelle für die Kundenzufriedenheit zu markieren und anschließend die Matrix auszuwählen, in der die Ränge ermittelt werden. Wichtig ist, dass du den Bezug für die gesamte Matrix fixierst, damit sich der Bezug nicht ändert, wenn du die Formel nach unten ziehst.
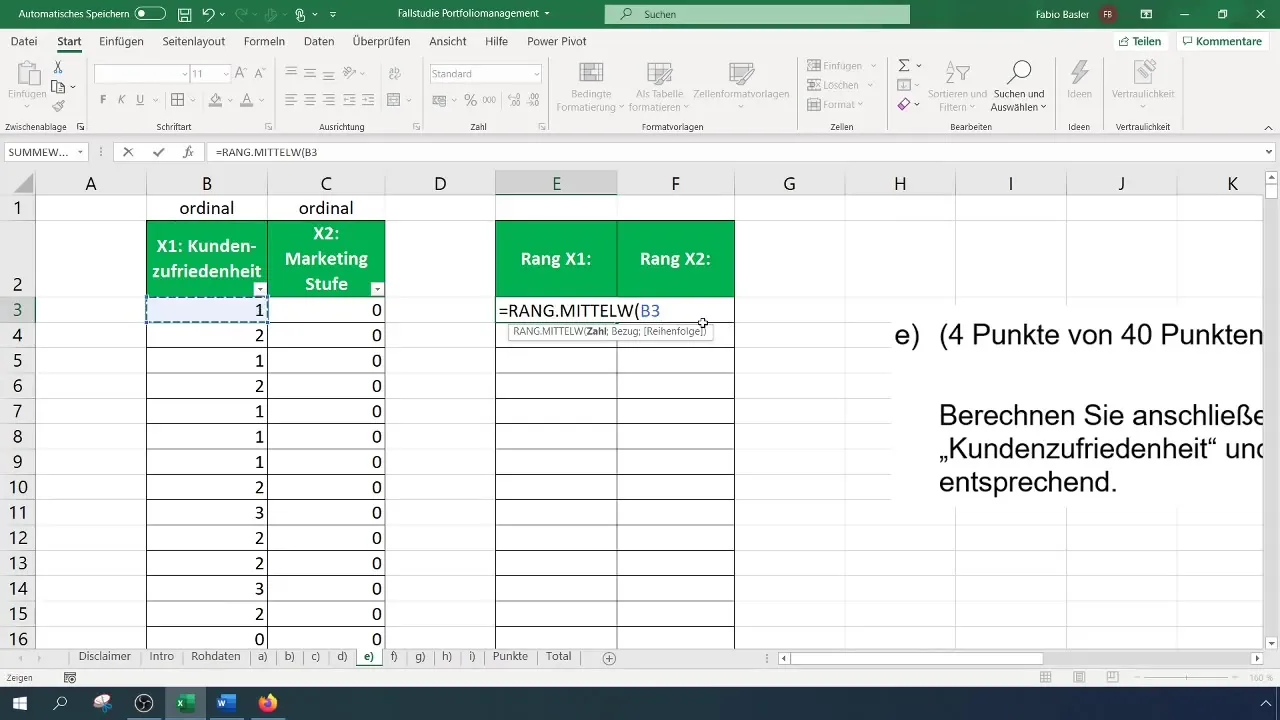
Starte mit der Berechnung, indem du die Formel tippst und danach die entsprechenden Parameter hinzufügst. Achte darauf, die richtige Reihenfolge in der Funktion einzuhalten. Definiere den Bezug auf deine Datenmatrix und wähle die gewünschte Sortierung, also aufsteigend oder absteigend.
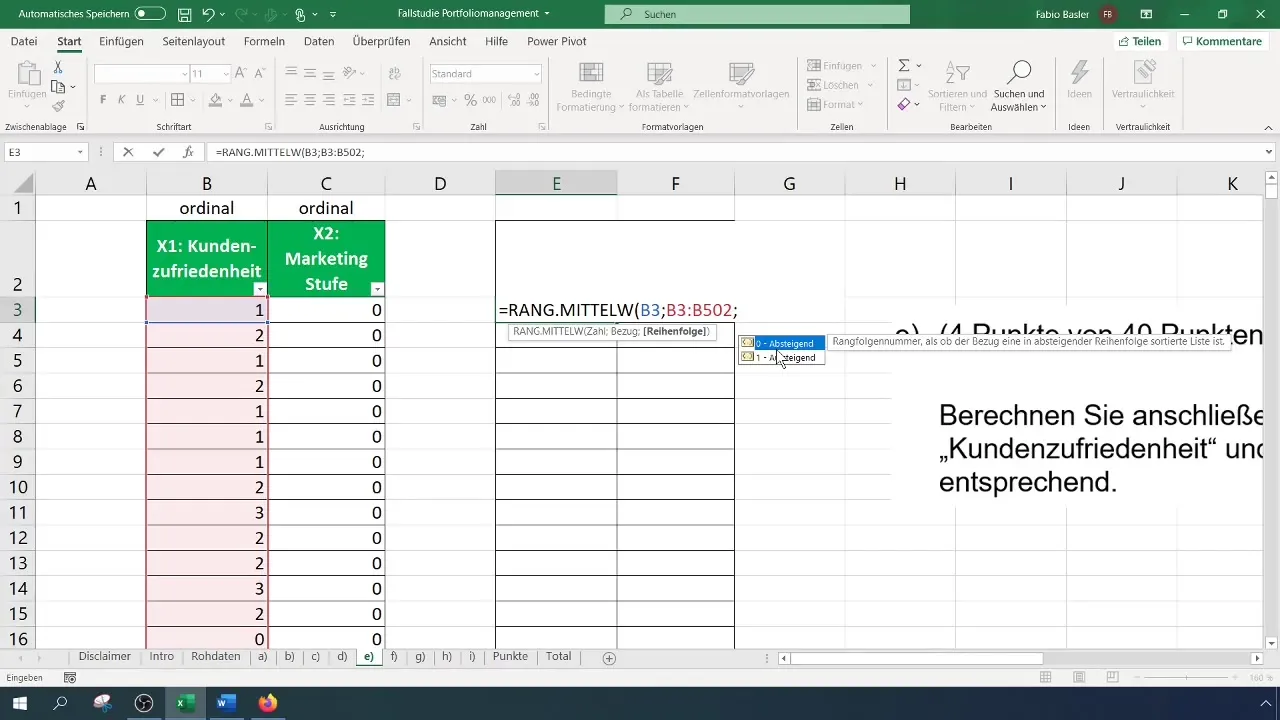
Wenn du die Ränge für die Marketingstufe (X2) berechnen möchtest, wiederholst du den gleichen Vorgang. Auch hier ist es wichtig, den gesamten Datenbereich festzuhalten, damit die Formel korrekt funktioniert, wenn du diese nach unten kopierst. Diese Schritte garantieren, dass die Ränge für jede Variable ordnungsgemäß ermittelt werden.
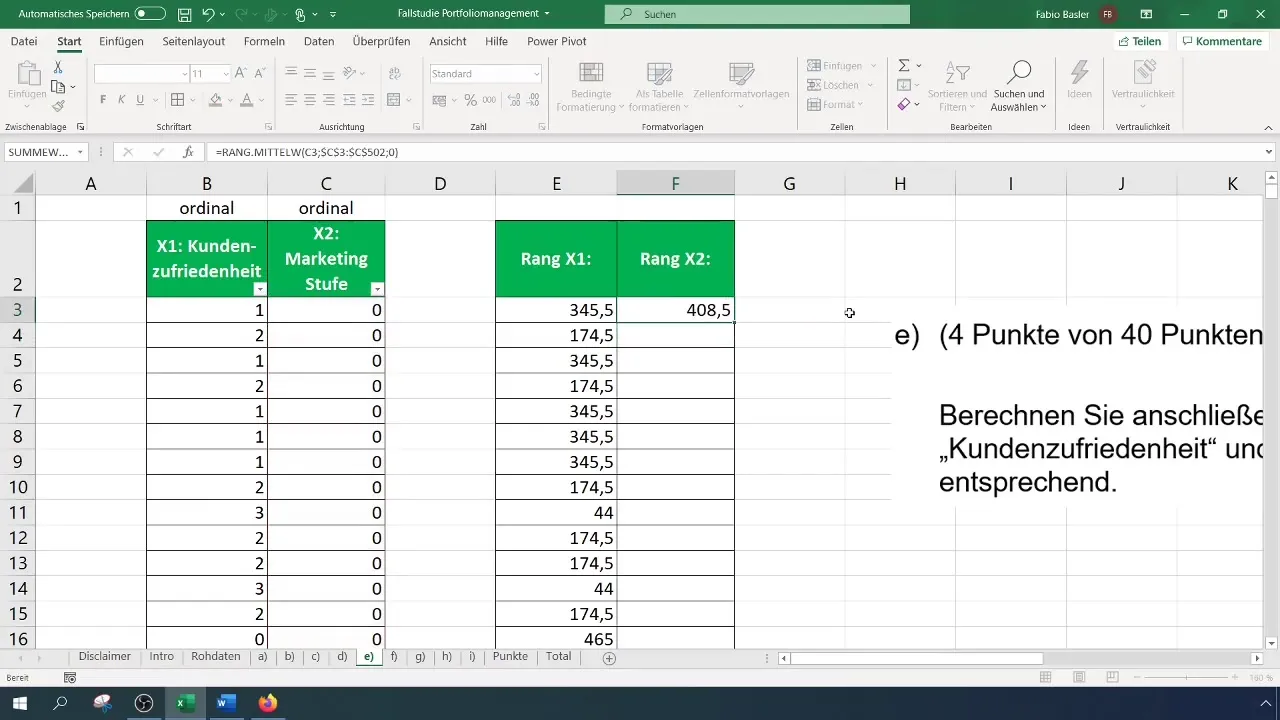
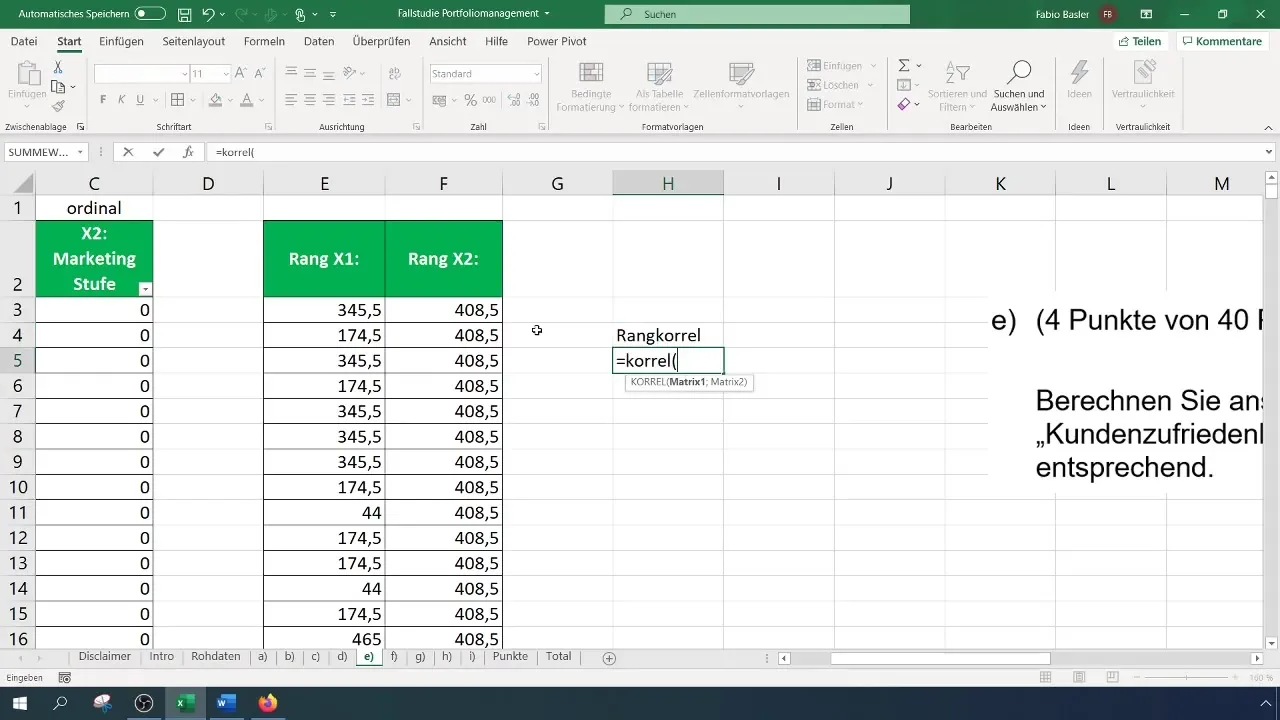
Sobald du die Ränge für beide Variablen hast, kannst du die Rangkorrelation berechnen. Das geschieht mit der Funktion „KORREL“. Diese Funktion ermöglicht es dir, die Ränge sowohl von X1 als auch von X2 anzuwählen und die Korrelation zu berechnen. Das Ergebnis wird dir die Stärke des Zusammenhangs zwischen den beiden Variablen angeben.
In deinem Fall ist die Korrelation 0,082, was auf einen schwachen positiven Zusammenhang hindeutet. Diese Zahl zeigt, dass zwar eine Tendenz besteht, dass höhere Marketingausgaben zu besserer Kundenzufriedenheit führen, dieser Zusammenhang jedoch nicht stark ist.
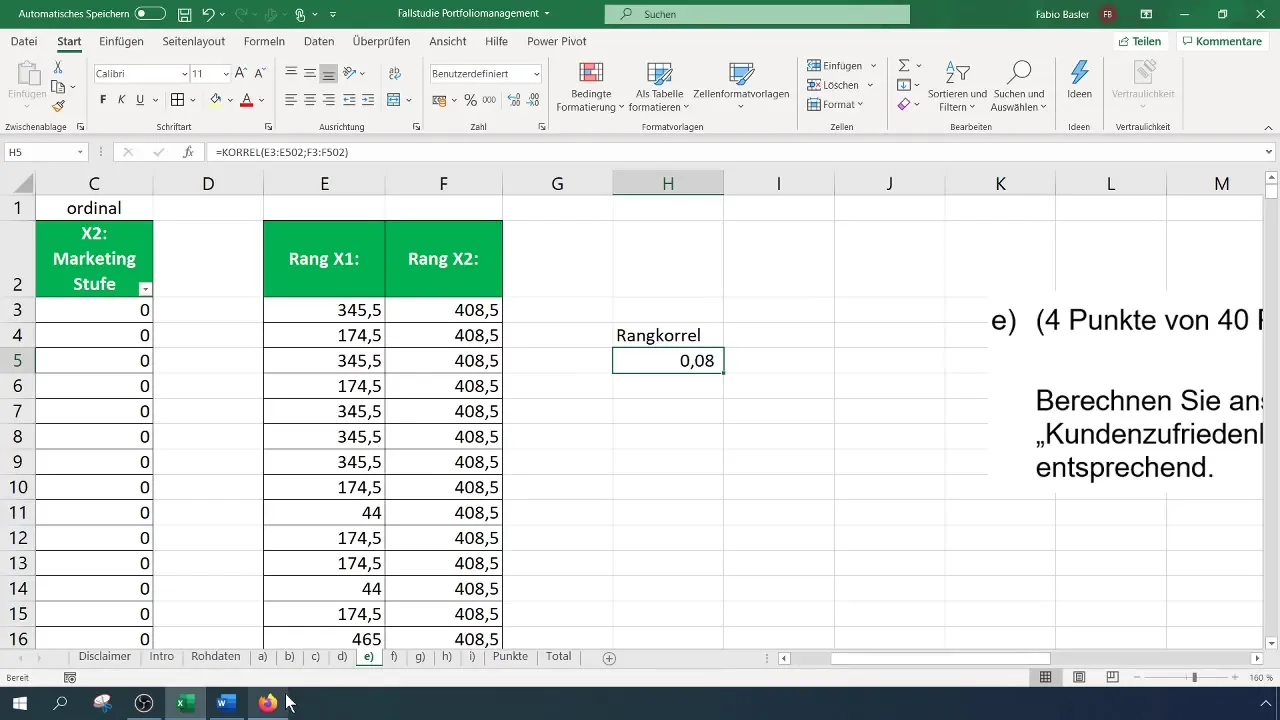
Letztlich solltest du die Interpretation deiner Ergebnisse dokumentieren. Eine Tabelle könnte dir helfen, um zu verdeutlichen, wo die Rangkorrelation steht, und die Beziehung zwischen den beiden Variablen klar darzustellen.
Der Ansatz der Rangkorrelationsanalyse hilft dabei, qualitative Einblicke in quantitative Daten zu gewinnen und zeigt dir, wie Marketingausgaben variieren könnten, ohne direkt die Zufriedenheit der Kunden zu erhöhen.
Zusammenfassung
In dieser Anleitung hast du gelernt, wie du die Rangkorrelationsanalyse in Excel durchführst. Zuallererst hast du deine Daten korrekt vorbereitet und anschließend die Ränge beider Variablen ermittelt. Schließlich hast du die Rangkorrelation berechnet, um den Zusammenhang zwischen der Marketingstufe und der Kundenzufriedenheit zu quantifizieren.
Häufig gestellte Fragen
Wie unterschiedlich sind Spearman und Kendall?Spearman und Kendall sind beide Rangkorrelationskoeffizienten, die allerdings unterschiedlich berechnet werden. Spearman basiert auf Rangunterschieden, während Kendall die Anzahl der Übereinstimmungen und Nichtübereinstimmungen genutzt.
Wie wähle ich die passende Korrelation aus?Die Wahl der Korrelation hängt von der Art der Daten ab. Für ordinal skalierte Daten ist Spearman geeignet, für metrische Daten wird oft Pearson verwendet.
Könnte ich eine Regression anstelle einer Korrelation verwenden?Ja, eine Regression kann nützlich sein, um den Einfluss einer oder mehrerer unabhängiger Variablen auf eine abhängige Variable zu untersuchen, die Korrelation zeigt lediglich eine Beziehung.


