Kontingenzanalyse in Excel: Zusammenhänge verstehen

Wenn du dich mit der Analyse von Daten beschäftigst, wirst du schnell auf die Notwendigkeit stoßen, Zusammenhänge zwischen verschiedenen Variablen zu erkennen. In diesem Tutorial werde ich dir zeigen, wie du in Excel eine Kontingenzanalyse durchführst, um die Beziehung zwischen zwei nominalen Variablen zu quantifizieren. Wir nutzen dafür ein praktisches Beispiel aus der Automobilzulieferindustrie, um zu verstehen, wie man aus den Daten wertvolle Erkenntnisse gewinnen kann.

Wichtigste Erkenntnisse

• Kontingenzanalyse ermöglicht die Untersuchung von Zusammenhängen zwischen zwei nominalen Variablen.
• Der Kontingenzkoeffizient quantifiziert die Stärke der Beziehung.
• Eine Pivottabelle in Excel ist ein unverzichtbares Werkzeug für die Analyse.

Schritt-für-Schritt-Anleitung zur Kontingenzanalyse

Schritt 1: Daten vorbereiten

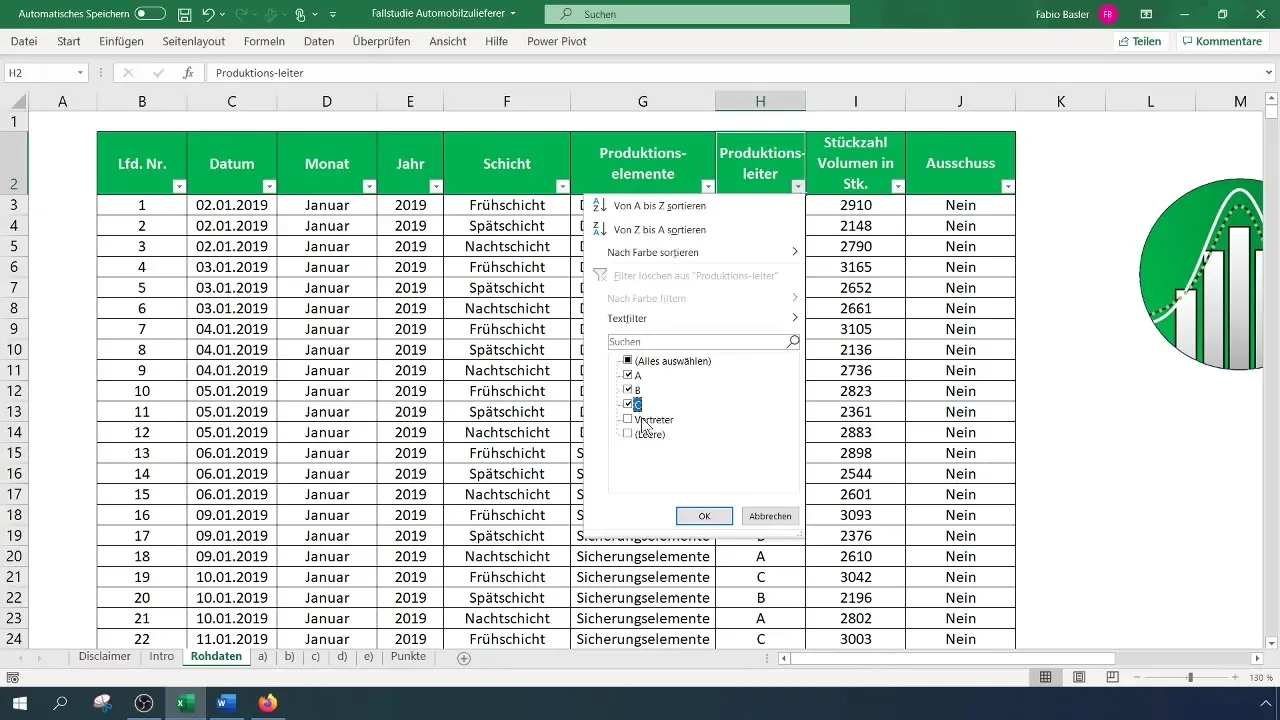
Bevor du mit der Kontingenzanalyse in Excel beginnst, musst du sicherstellen, dass die Daten, mit denen du arbeitest, korrekt aufbereitet sind. Entferne alle Filtereinstellungen, um die gesamte Sicht auf die Daten zu gewährleisten.

Erstelle eine Übersicht, die den Produktionsleiter und die Informationen zu Ausschuss als nominale Daten enthält. In unserem Fall konzentrieren wir uns auf die Schichtführer A, B und C und lassen alle anderen Vertreter außen vor.

Schritt 2: Pivottabelle erstellen

Um die Kontingenzanalyse durchzuführen, musst du eine zweidimensionale Häufigkeitsverteilung erstellen, die dir zeigt, wie oft jede Kombination von Produktionsleiter und Ausschuss vorkommt. Gehe dazu in die Menüleiste auf "Einfügen" und wähle "Pivottabelle".

Wähle den relevanten Datenbereich aus und bestätige, dass die Überschriften korrekt erkannt werden. Deine Pivottabelle wird nun erstellt und du kannst die Felder für Produktionsleiter und Ausschuss gegenüberstellen.

Schritt 3: Häufigkeiten analysieren

Nachdem du deine Pivottabelle erstellt hast, kannst du die absoluten Häufigkeiten ermitteln. Platziere die Merkmale in den Zeilen und Spalten der Pivottabelle. Dies zeigt dir, wie viele Ausschüsse pro Schichtleiter kamen.

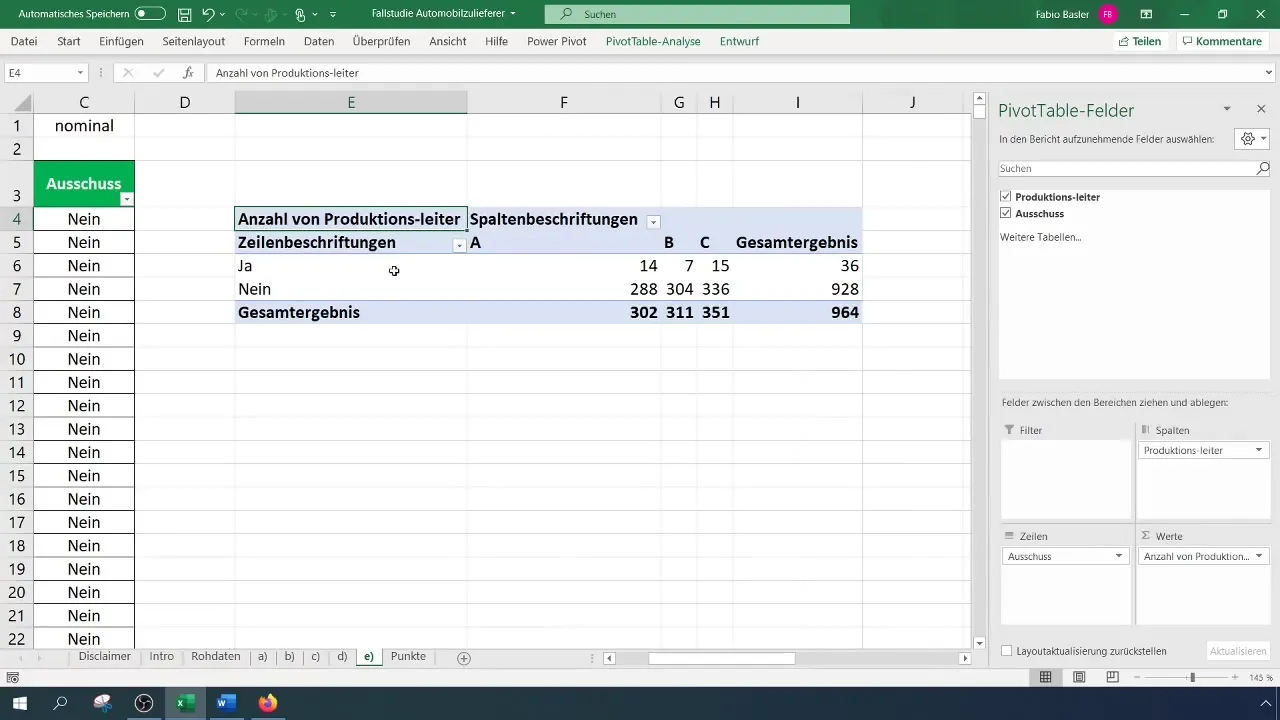
Sieh dir die Pivottabelle an und analysiere die Ergebnisse. Beachte insbesondere die Verteilung der Variablen, um festzustellen, bei welchem Schichtleiter der Ausschuss am häufigsten oder am seltensten auftritt.

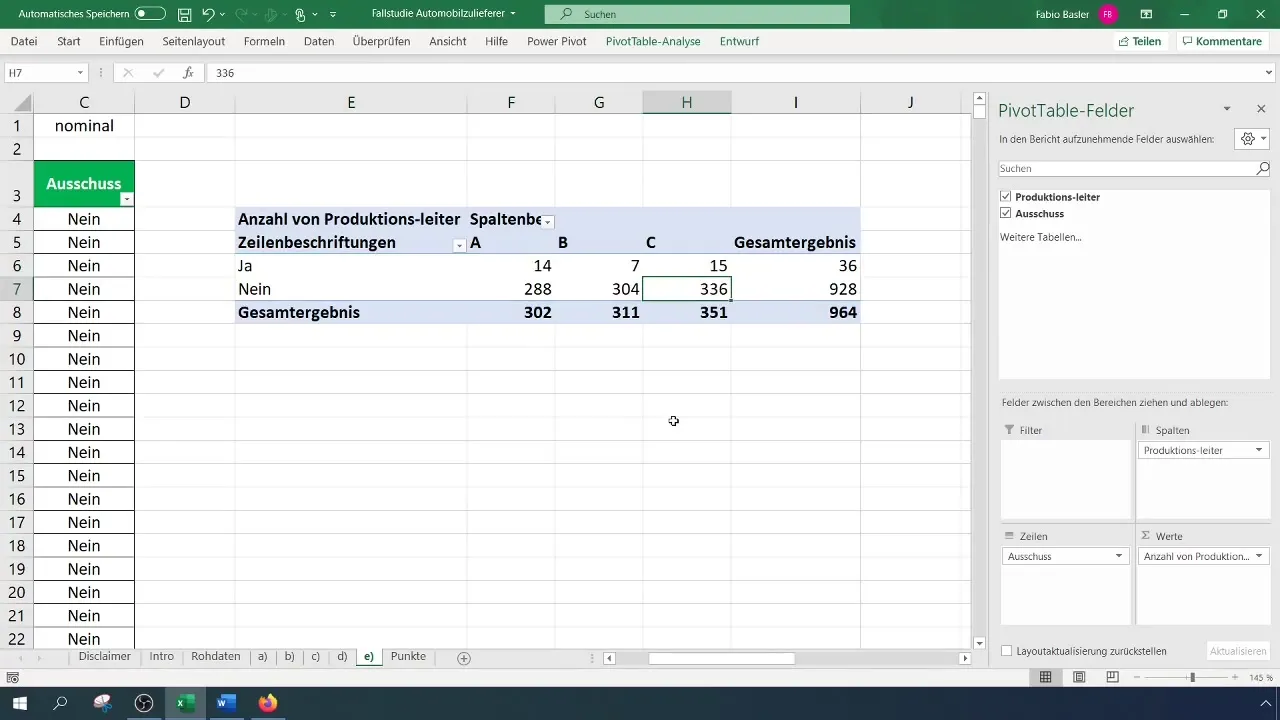
Schritt 4: Erwartete Häufigkeiten berechnen

Um den Kontingenzkoeffizienten zu berechnen, musst du die erwarteten absoluten Häufigkeiten bestimmen. Die allgemeine Formel lautet: (N_{ij} = \frac{(R_i \times C_j)}{N}), wobei (R) die Randhäufigkeit der Zeilen und (C) die Randhäufigkeit der Spalten darstellt.

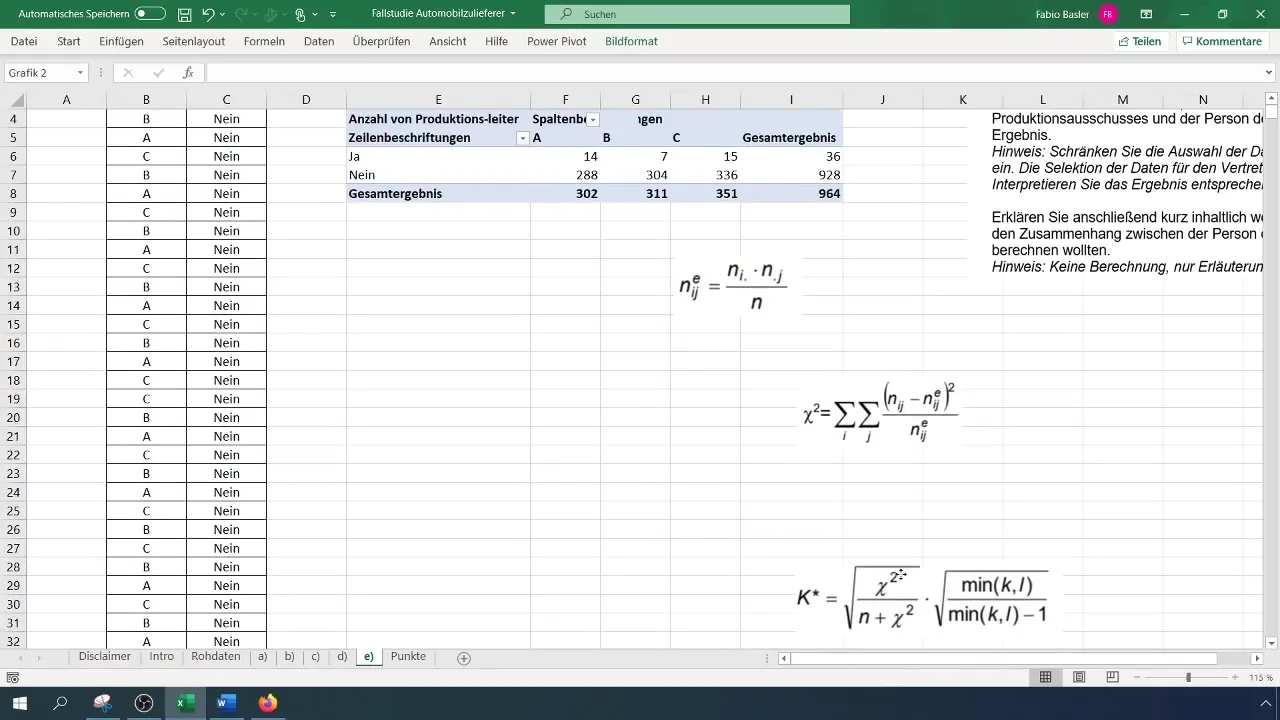
Wende diese Berechnung auf die Werte in deiner Pivottabelle an. Achte darauf, eine separate Tabelle für die erwarteten Häufigkeiten zu erstellen, um die Analysen übersichtlich zu halten.

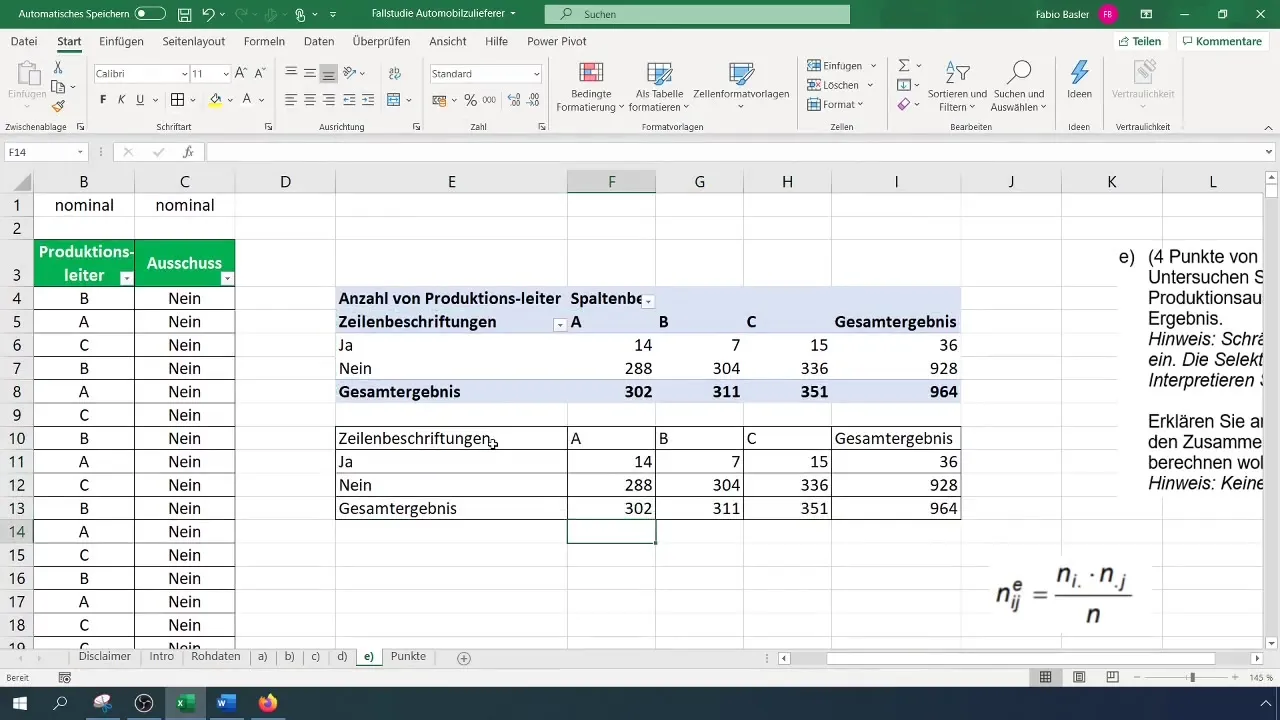
Schritt 5: Chi-Quadrat-Wert berechnen

Berechne nun den Chi-Quadrat-Wert, um die Beziehung zwischen den Variablen quantitativ zu erfassen. Die Formel lautet:

[ \chi^2 = \sum \frac{(O{ij} - E{ij})^2}{E_{ij}} ]

Hierbei ist (O) die beobachtete Häufigkeit und (E) die erwartete Häufigkeit.

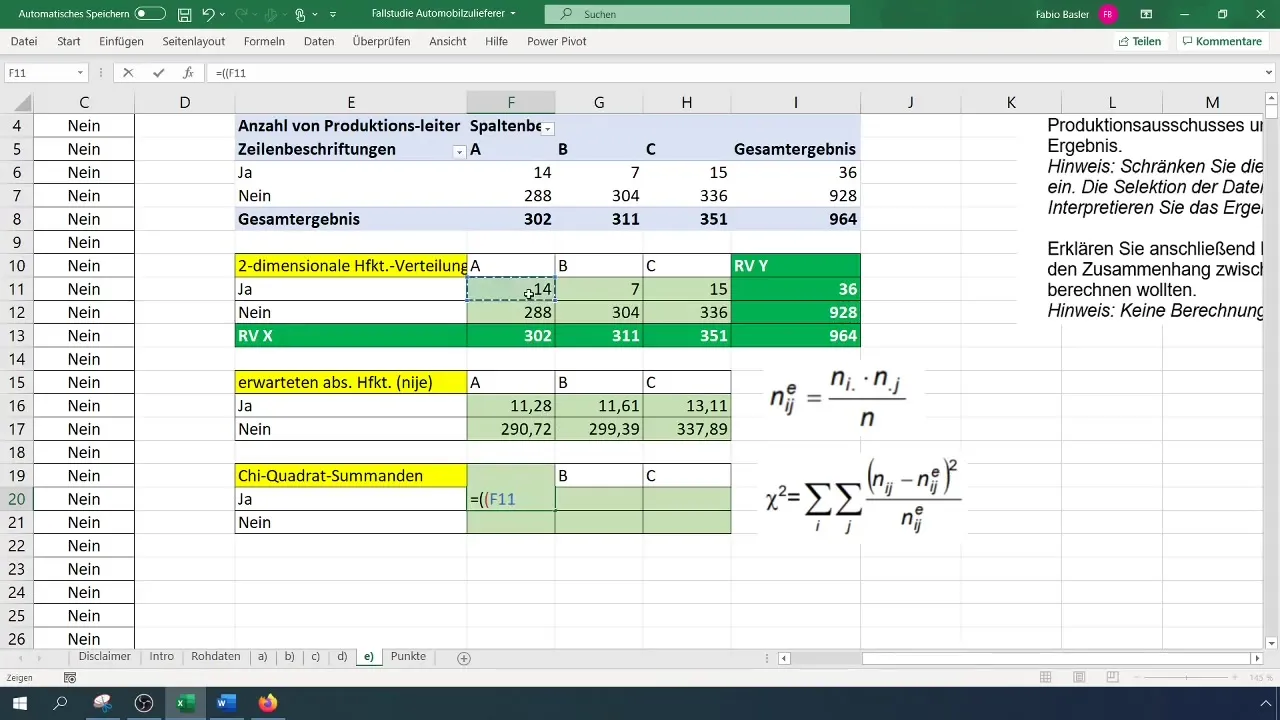
Ziehe dazu die Differenzen zwischen den beobachteten und erwarteten Häufigkeiten und quadriere diese.

Schritt 6: Kontingenzkoeffizienten berechnen

Der letzte Schritt besteht darin, den Kontingenzkoeffizienten zu berechnen. Die Formel zur Berechnung lautet:

[ K = \sqrt{\frac{\chi^2}{N}} ]

Verwende den zuvor berechneten Chi-Quadrat-Wert und die Gesamtanzahl der Beobachtungen (N).

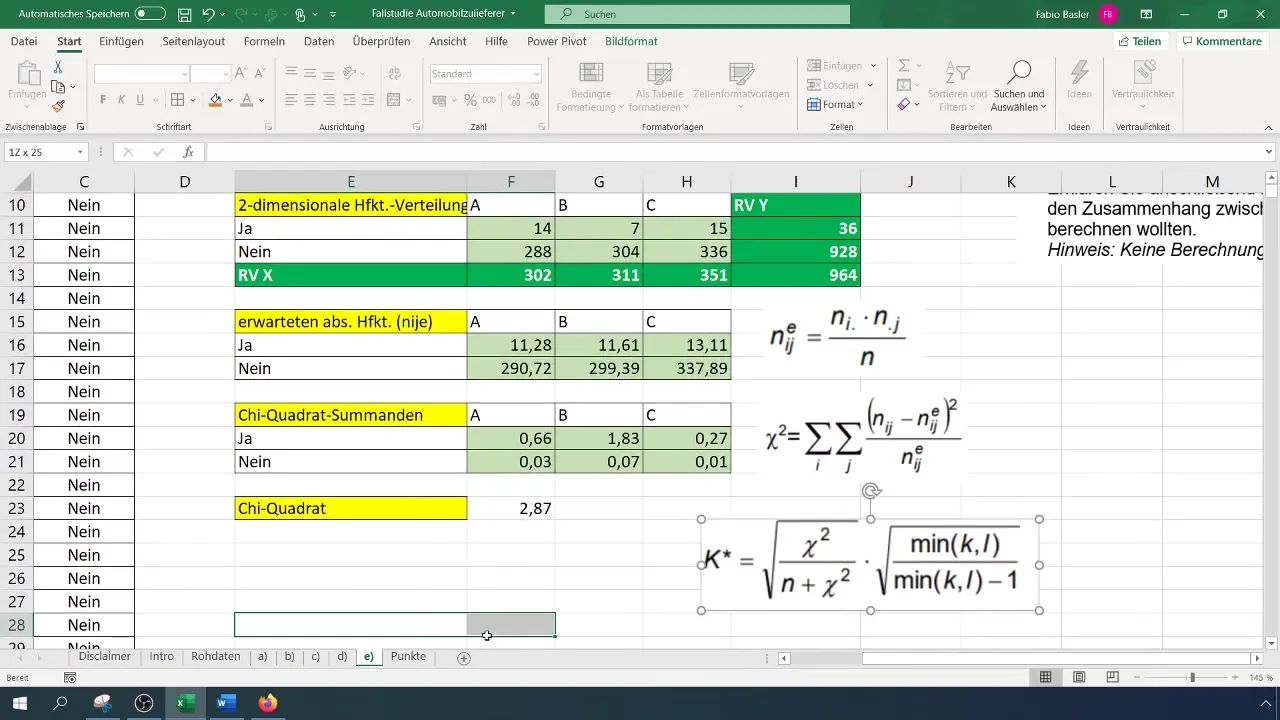
Nachdem du den Kontingenzkoeffizienten berechnet hast, kannst du das Resultat interpretieren. Unsere Analyse hat uns gezeigt, dass der Kontingenzkoeffizient von 0,077 einen schwachen Zusammenhang zwischen den Variablen aufzeigt.

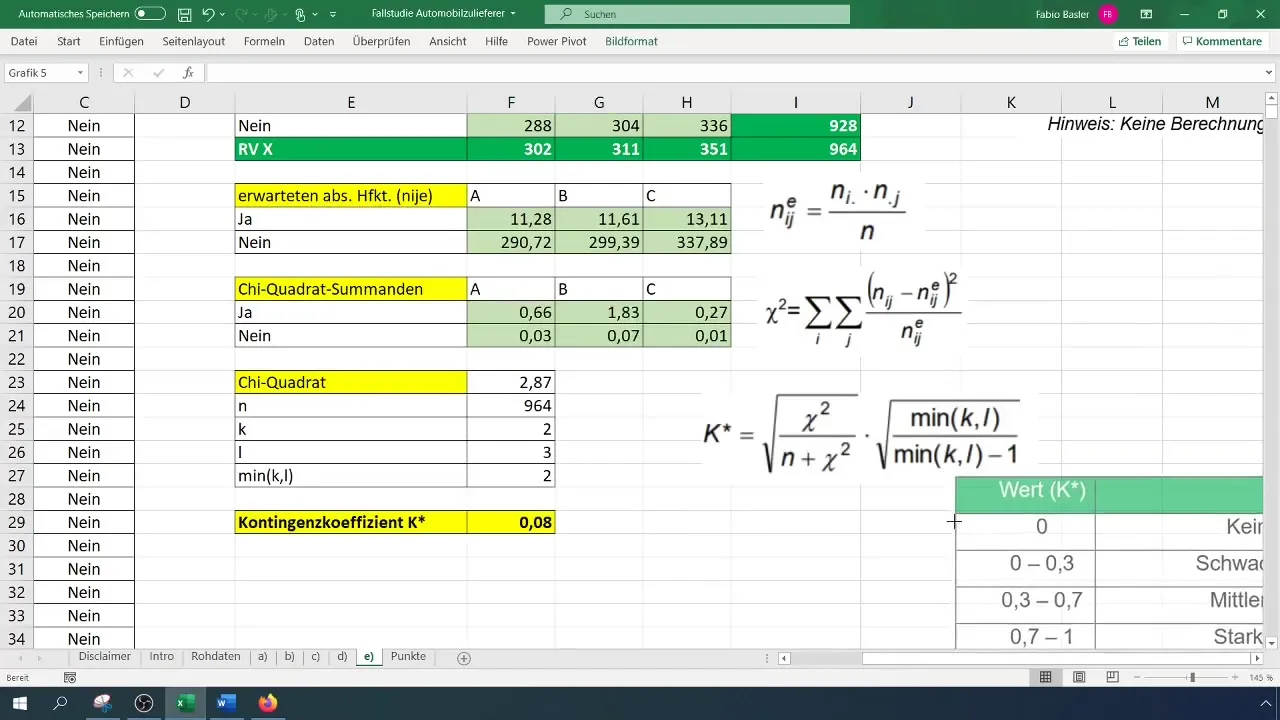
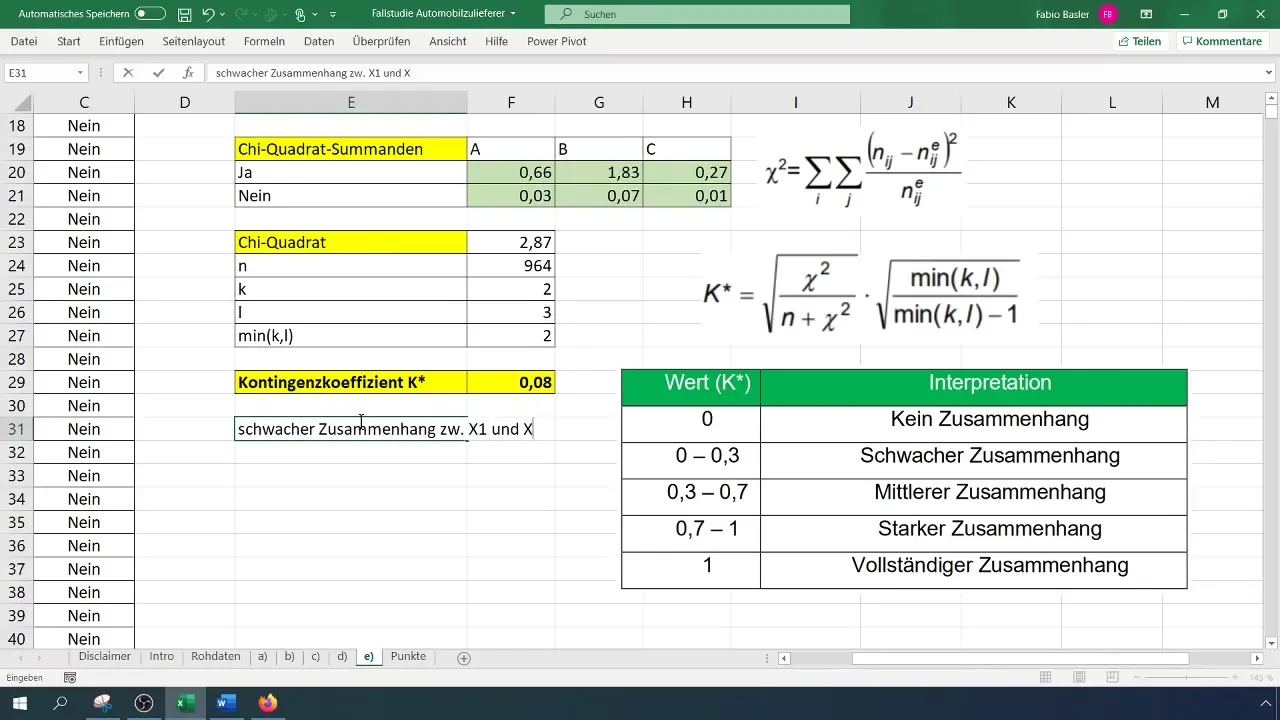
Schritt 7: Interpretation der Ergebnisse

Die letzten Schritte deiner Analyse bestehen darin, die Ergebnisse zu interpretieren. Ein Kontingenzkoeffizient nahe 0 zeigt, dass kaum ein Zusammenhang zwischen den Variablen besteht. Ein Wert von 0,08 deutet darauf hin, dass der Produktionsleiter keinen signifikanten Einfluss auf das Auftreten von Ausschuss hat.

Zusammenfassung

In dieser Anleitung hast du erfahren, wie du die Kontingenzanalyse in Excel durchführst, um Zusammenhänge zwischen nominalen Variablen zu erkennen. Du hast gelernt, wie du deine Daten vorbereitest, eine Pivottabelle erstellst und die notwendigen Berechnungen für den Kontingenzkoeffizienten durchführst.