Statistische Tests sind ein zentraler Bestandteil der Datenanalyse und Entscheidungsfindung. Besonders im Bereich der Biotechnologie kann es entscheidend sein, Hypothesen über die Erfolgsquote von Wirkstoffen zu überprüfen. Im Rahmen dieses Tutorials lernst du, wie du einen Ein-Stichproben-Test (1-SP-Test) für den Erwartungswert mit bekannter Varianz effizient in Excel durchführst.
Wichtigste Erkenntnisse
Dieser Leitfaden vermittelt dir:
- Die theoretischen Grundlagen des 1-SP-Tests.
- Schritte zur Durchführung des Tests in Excel.
- Die Interpretation der Ergebnisse.
Vorbereitung der Daten
Um den 1-SP-Test in Excel durchzuführen, benötigst du zunächst die relevanten Daten. In unserem Beispiel gehen wir von einer Situation aus, in der du die Erfolgsquote von Wirkstoffen analysierst. Es ist bekannt, dass die durchschnittliche Erfolgsquote früher 59% betrug, bei einer Standardabweichung von 19. Zunächst solltest du deine Daten in eine Excel-Tabelle einpflegen.
Vergewissere dich, dass deine Daten in Spalten organisiert sind, damit du später darauf zugreifen kannst. Eine schöne Übersichtlichkeit hilft dir, die einzelnen Schritte leichter nachzuvollziehen.
Testüberblick
Der 1-SP-Test dient dazu, zu überprüfen, ob sich der durchschnittliche Erfolgswert signifikant von einem vorgegebenen Wert unterscheidet. In diesem Fall überprüfen wir, ob die Erfolgsquote von 59% in der Zukunft deutlich erhöht werden kann.
Hypothesen formulieren
Die Hypothesen, die du für den Test aufstellst, sind entscheidend:
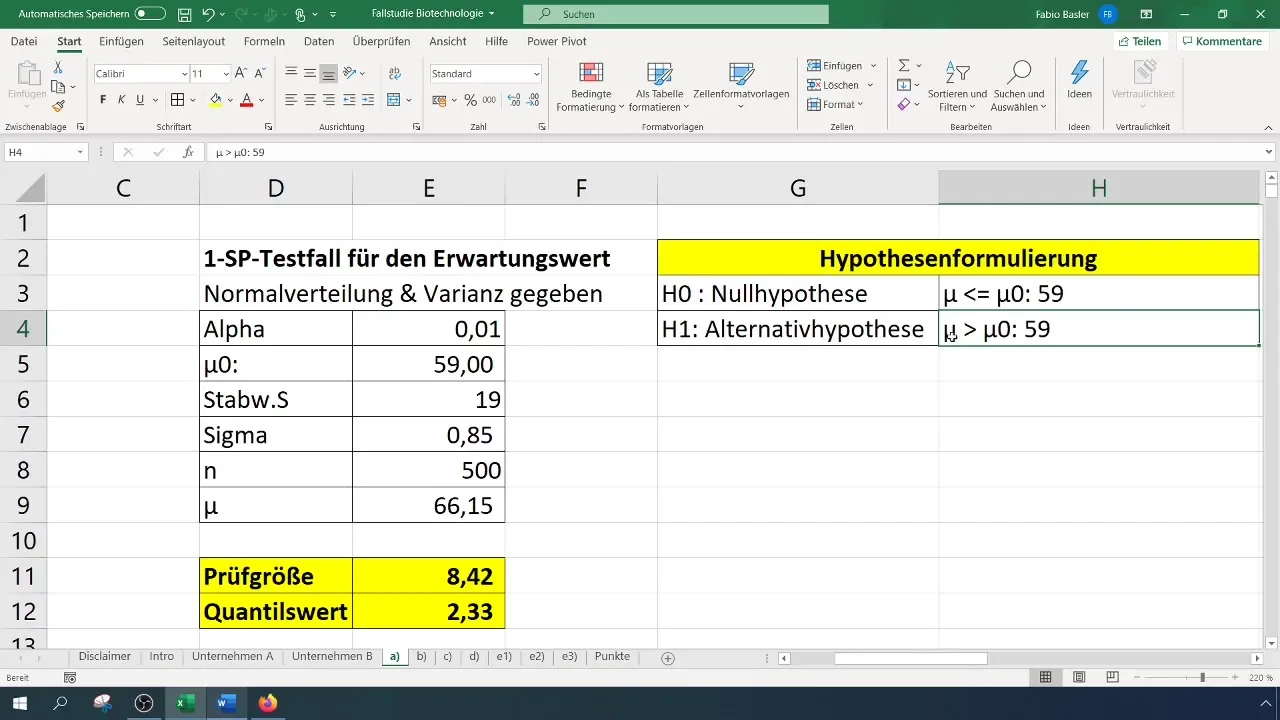
- Nullhypothese (H0): Der wahre Erwartungswert ist gleich 59 (σ = 59%).
- Alternativhypothese (H1): Der wahre Erwartungswert ist größer als 59%.
Bei der Formulierung der Hypothesen sollte der Fokus darauf liegen, was genau getestet werden muss und wie sich das in deinem Kontext darstellt.
Es ist wichtig, den Unterschied zwischen der Nullhypothese und der Alternativhypothese klar zu erkennen, da sie die Basis für die folgenden Berechnungen bilden.
Erhebung der Stichprobe
Für unseren Test nehmen wir eine Stichprobe von 500 Wirkstoffen. Es ist wichtig zu beachten, dass die Auswahl der Stichprobe repräsentativ ist und über die entsprechende Methode garantieren sollte, dass sich deine Ergebnisse realistischerweise auf die Gesamtpopulation übertragen lassen.
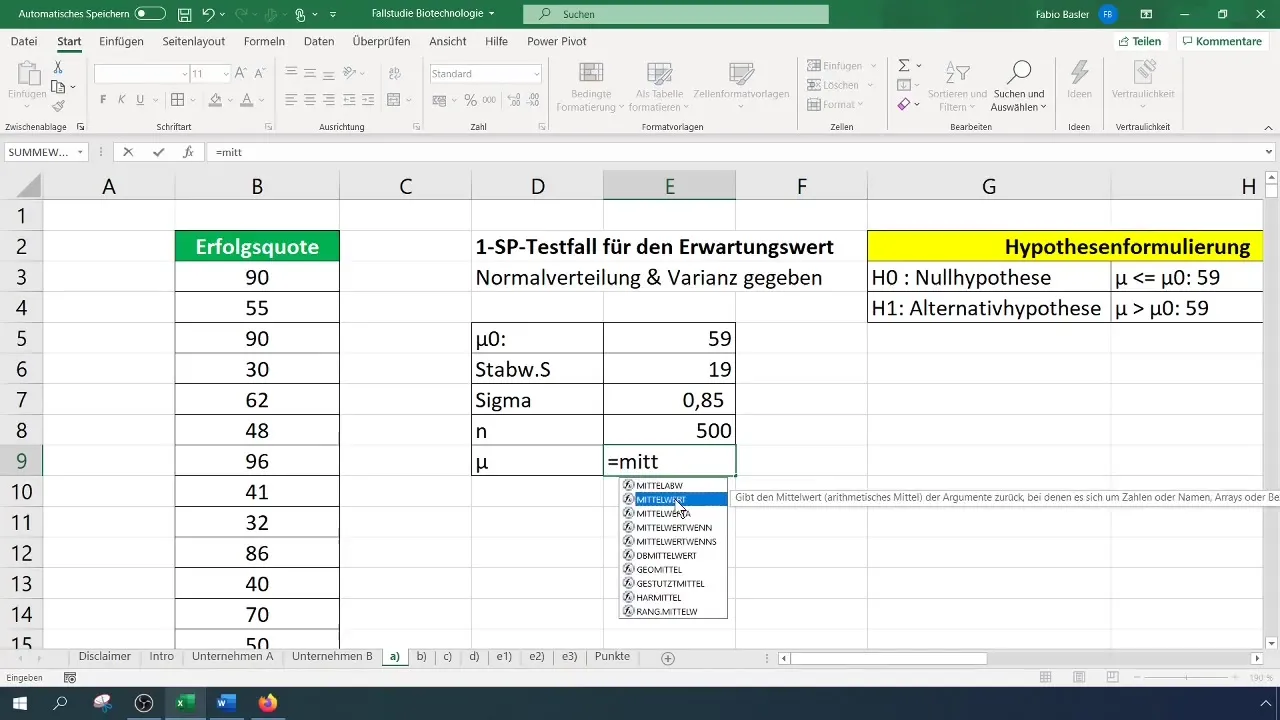
Für den Test berechnest du zunächst den arithmetischen Mittelwert. Das sollte einfach bewerkstelligt werden, indem du in Excel die entsprechende Formel verwendest.
Berechnung der Prüfgröße
Die Prüfgröße für einen 1-SP-Test wird durch folgende Formel bestimmt:
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Hier steht (\bar{x}) für den Mittelwert deiner Stichprobe, (\mu_0) für den angenommenen Mittelwert (in diesem Fall 59), (\sigma) für die Standardabweichung (hier 19), und (n) für die Anzahl der Stichproben (500).
Nachdem du die Werte in die Formel eingesetzt hast, berechne die Prüfgröße, um festzustellen, ob sie signifikant ist oder nicht.
Ermittlung des kritischen Wertes
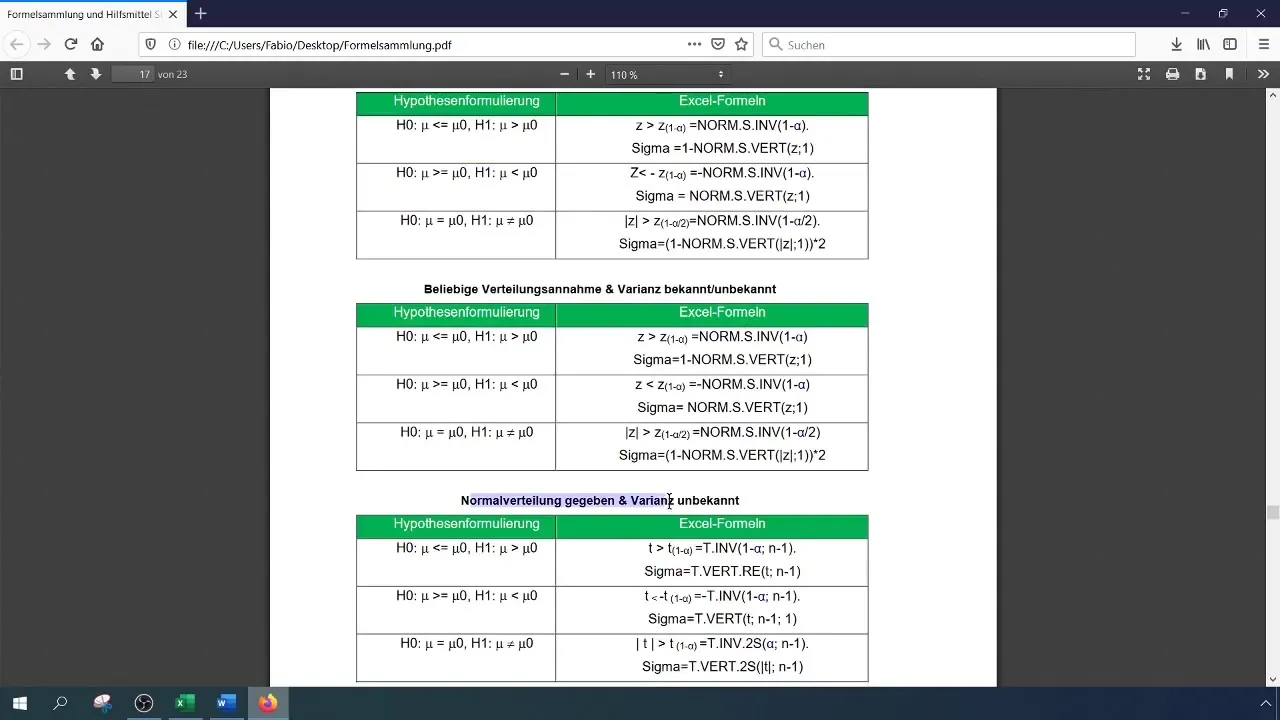
Für einen Signifikanzgrad von 1% (0,01) musst du den kritischen Wert ablesen oder berechnen. Du kannst dies in Excel mit der Funktion NORM.S.INV tun.
Die Formel lautet:
[ \text{NORM.S.INV}(1 - \alpha) ]
Hierbei ist (\alpha) das Signifikanzniveau (0,01). Der ermittelte Wert wird als Grundlage für den Vergleich mit der Prüfgröße verwendet.
Durchführung des Tests
Nachdem du nun sowohl die Prüfgröße als auch den kritischen Wert hast, vergleichst du beide:
- Falls die Prüfgröße größer als der kritische Wert ist, wird die Nullhypothese verworfen.
- Ansonsten kannst du die Nullhypothese nicht ablehnen.
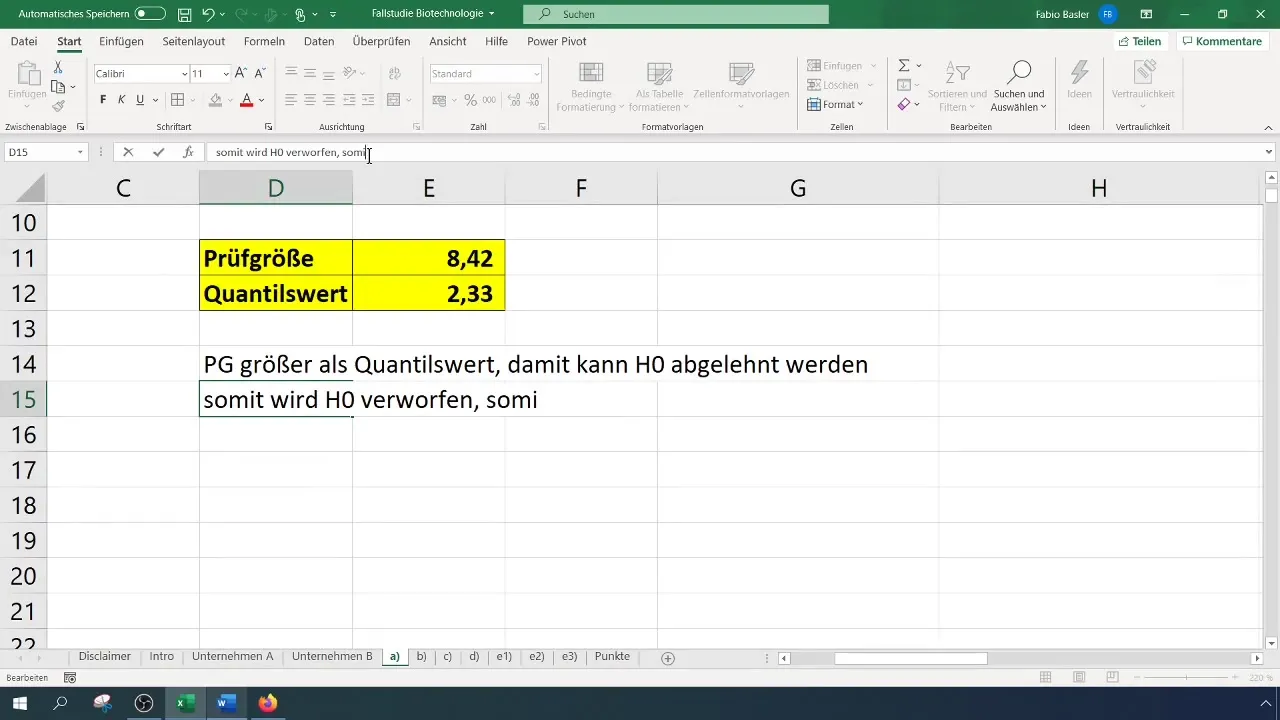
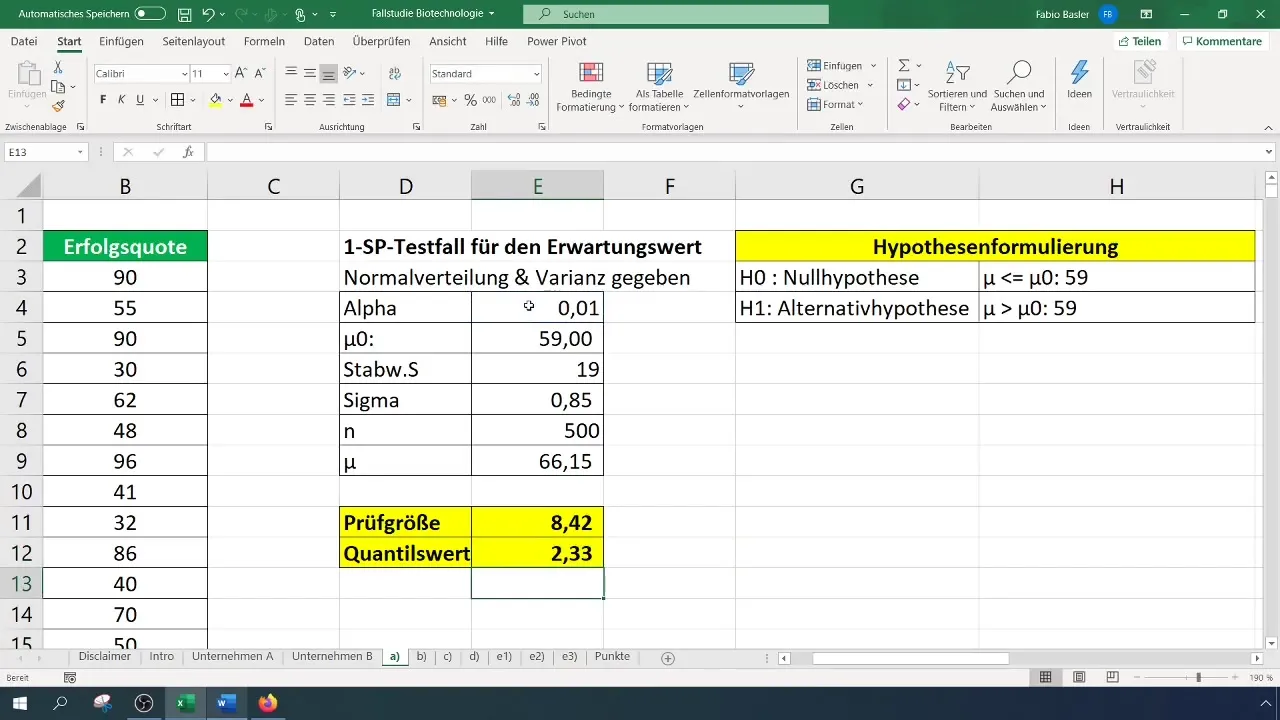
In unserem Fall ergibt sich eine Prüfgröße von 8,4, die den kritischen Wert von 2,33 übersteigt. Daher können wir die Nullhypothese ablehnen. Dies deutet darauf hin, dass die Erfolgsquote signifikant verbessert wurde.
Interpretation der Ergebnisse
Nachdem du den Test durchgeführt und die Ergebnisse ermittelt hast, solltest du sie in einem klaren Kontext interpretieren. Die Ablehnung der Nullhypothese bedeutet, dass der getestete neue Wert sich signifikant von der Vergangenheit, in diesem Fall den 59%, unterscheidet.
Diese Informationen sind für die strategische Entscheidungsfindung in deinem Unternehmen von enormer Bedeutung. Sie bestätigen, dass die Efforts zur Verbesserung der Erfolgsquote wirksam waren.
Zusammenfassung
In diesem Tutorial hast du gelernt, wie du einen 1-SP-Test für den Erwartungswert in Excel durchführst. Anhand einer Fallstudie konntest du die Schritte vom Hypothesen aufstellen über die Datenberechnung bis hin zur Interpretation der Ergebnisse nachvollziehen. Diese Kenntnisse sind nicht nur für wissenschaftliche Auswertungen, sondern auch für praktische Anwendungen im Unternehmen wertvoll.
Häufig gestellte Fragen
Was ist der 1-SP-Test?Der 1-SP-Test ist ein statistischer Test, um zu überprüfen, ob der Mittelwert einer Stichprobe signifikant von einem vorgegebenen Wert abweicht.
Wie formuliere ich Hypothesen für den Test?Die Hypothesen bestehen aus einer Nullhypothese (H0) und einer Alternativhypothese (H1), die den zu überprüfenden Zustand dokumentieren.
Wie berechne ich die Prüfgröße?Die Prüfgröße wird durch die Formel ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ) bestimmt.
Was passiert, wenn die Prüfgröße größer ist als der kritische Wert?Wenn die Prüfgröße größer als der kritische Wert ist, wird die Nullhypothese verworfen.
Welche Rolle spielt das Signifikanzniveau?Das Signifikanzniveau gibt an, mit welcher Wahrscheinlichkeit du bereit bist, einen Fehler zu akzeptieren, wenn du die Nullhypothese fälschlicherweise ablehnst.


