Der Zweistichproben-t-Test ist ein essentielles Werkzeug in der Statistik, wenn du den Unterschied zwischen zwei Mitteln untersuchen möchtest. In diesem Tutorial erfährst du, wie du diesen Test einfach und effektiv in Excel durchführst. Anhand eines Beispiels aus der Biotechnologie wirst du lernen, die Erfolgsquoten zwei konkurrierender Unternehmen zu vergleichen und statistisch zu analysieren.
Wichtigste Erkenntnisse
- Anwendung des zweistichproben-t-Tests zur Analyse des Unterschieds zwischen zwei Mittelwerte.
- Formulierung und Überprüfung von Hypothesen.
- Verwendung von Excel zur Berechnung und Darstellung der Ergebnisse.
Schritt-für-Schritt-Anleitung
Zunächst einmal beginnen wir mit der Erstellung der notwendigen Daten und der Durchführung des Tests in Excel.
Schritt 1: Daten vorbereiten
Beginne mit dem Sammeln der Rohdaten zu den Erfolgsquoten der beiden Unternehmen. Angenommen, du hast die Daten von Unternehmen A und B vorliegen. Dabei hast du eine Stichprobe von 100 Datensätzen pro Unternehmen.

Schritt 2: Stichprobenumfang und Mittelwerte berechnen
Erstelle eine Tabelle in Excel, um die Stichproben und deren Mittelwerte gegenüberzustellen. Berechne zunächst den Stichprobenumfang (N) für beide Unternehmen, sowie den Mittelwert (X).

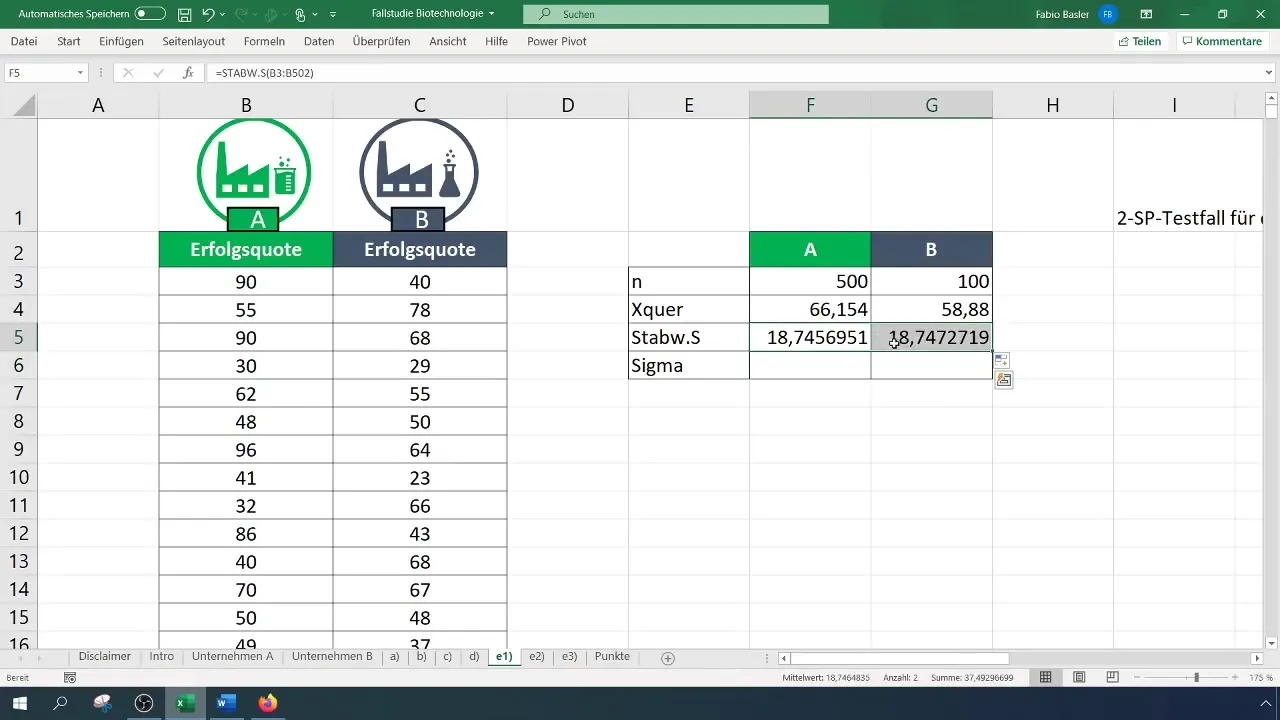
Schritt 3: Standardabweichungen ermitteln
Berechne die Standardabweichung für beide Unternehmen. Diese Werte sind wichtig, um die Varianz und die anschließenden Berechnungen durchzuführen.
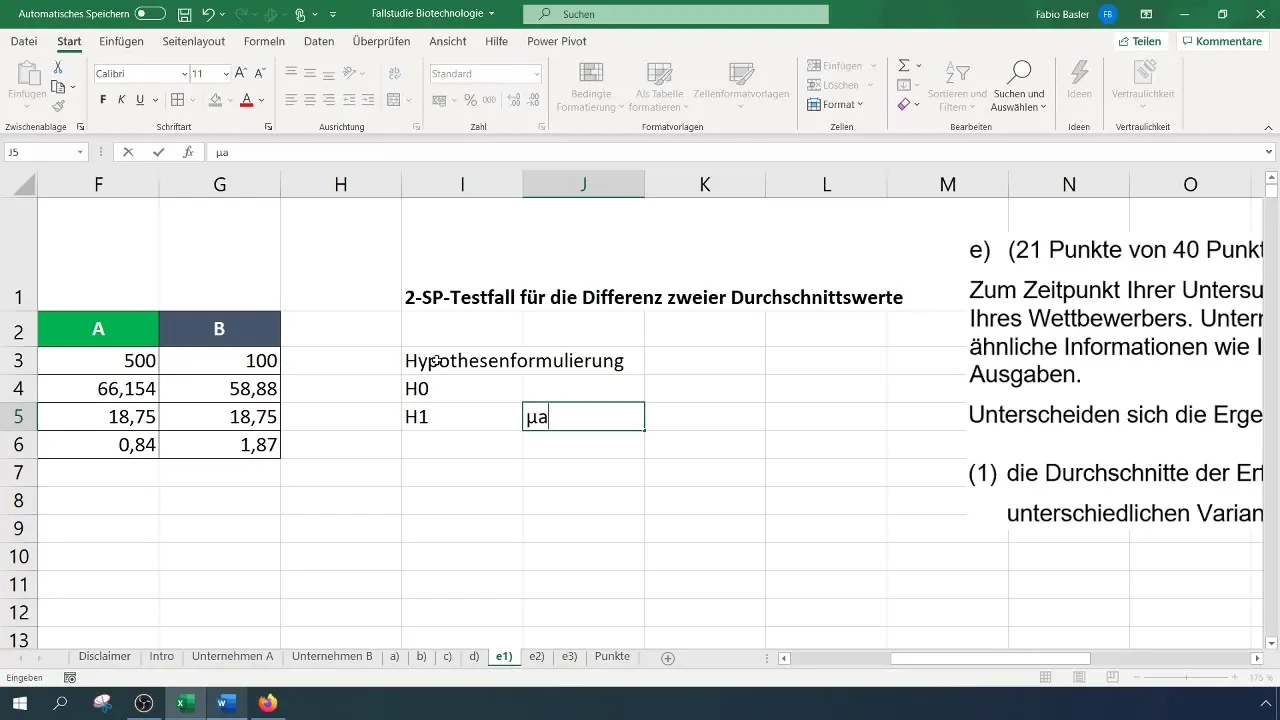
Schritt 4: Hypothesen formulieren
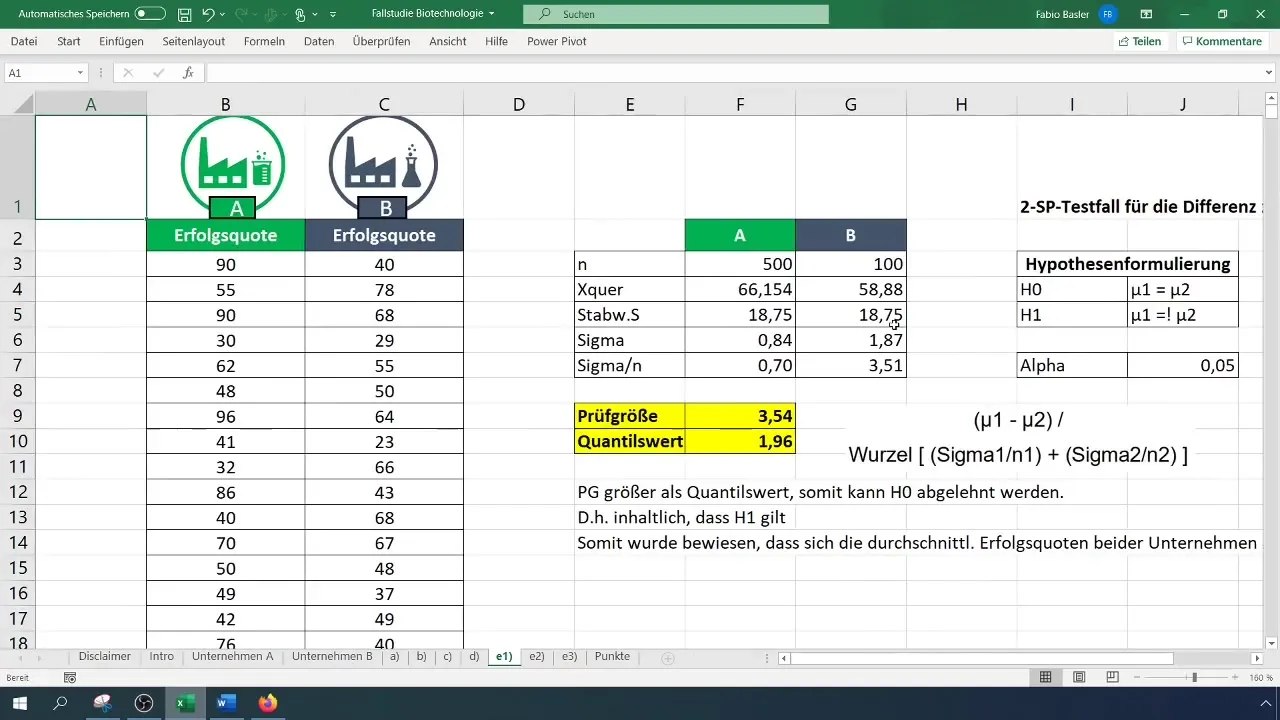
Formuliere die Nullhypothese (H_0): Die Durchschnittswerte der Erfolgsquoten der Unternehmen A und B sind gleich. Die Alternativhypothese (H_1): Die Durchschnittswerte der Erfolgsquoten sind unterschiedlich.
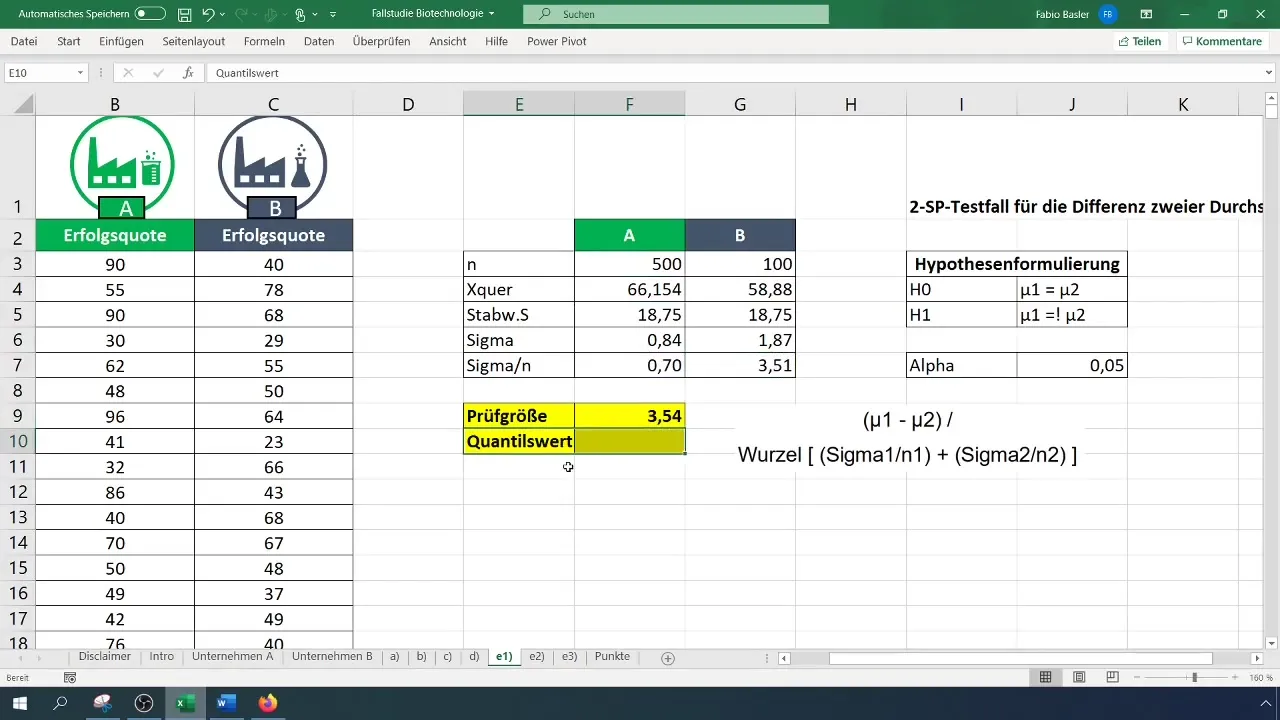
Schritt 5: Prüfgröße berechnen
Um die Prüfgröße zu berechnen, verwende die Formel für den t-Test. Berechne die Differenz der Mittelwerte und teile sie durch die Wurzel der Summe der Varianzen je Stichprobe.
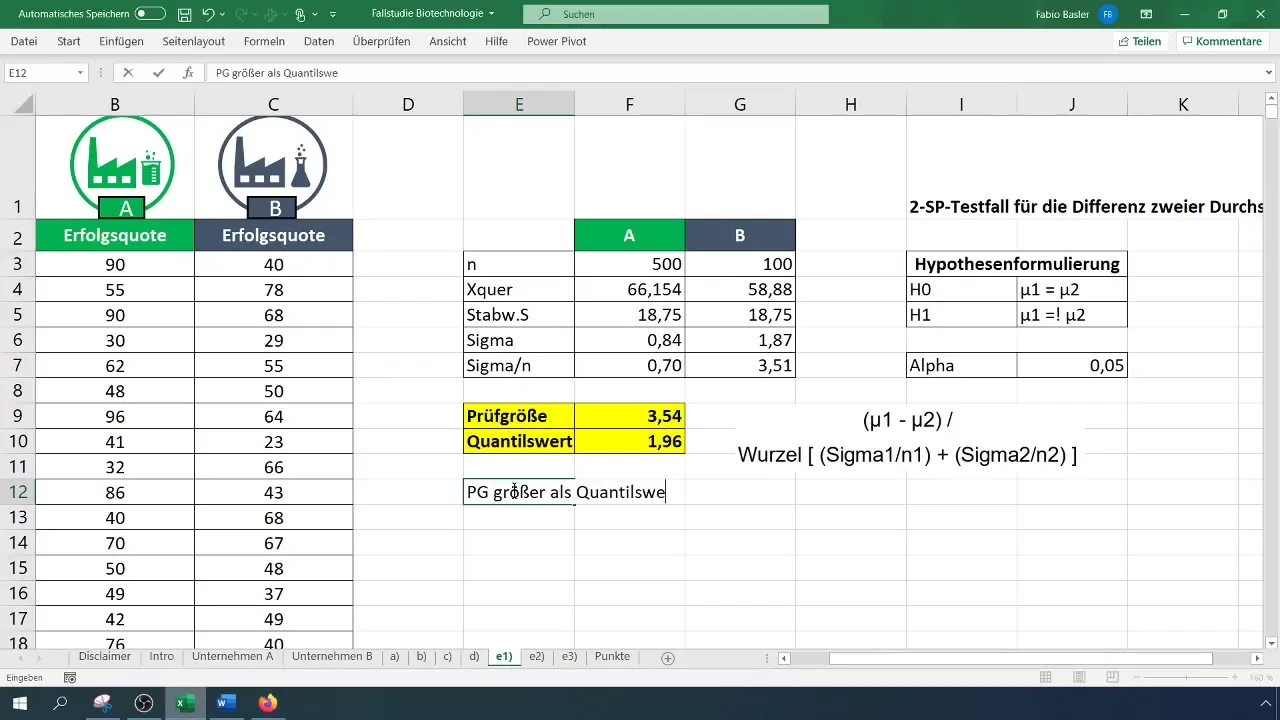
Schritt 6: Kritischen Wert ermitteln
Nutze die zweiseitige t-Verteilung, um den kritischen Wert zu finden. Setze das Alpha-Niveau auf 0,05. Überprüfe die t-Verteilungstabelle oder berechne den Faktor direkt in Excel.
Schritt 7: Entscheidung über die Hypothese treffen
Vergleiche die berechnete Prüfgröße mit dem kritischen Wert. Wenn die Prüfgröße größer ist als der kritische Wert, lehne die Nullhypothese (H_0) ab und bestätige dadurch die Alternativhypothese (H_1).
Schritt 8: Ergebnisinterpretation
Schließlich interpretiere das Ergebnis. In diesem Beispiel wurden die durchschnittlichen Erfolgsquoten der beiden Unternehmen als signifikant unterschiedlich festgestellt.
Zusammenfassung
Du hast gelernt, wie du einen Zweistichproben-t-Test in Excel durchführst, um die Unterschiede in den Mittelwerten zweier Gruppen zu untersuchen. Die Schritte von der Datenvorbereitung über die Hypothesenformulierung bis hin zur Interpretation der Ergebnisse sind entscheidend, um valide und informierte Entscheidungen zu treffen.
Häufig gestellte Fragen
Was ist ein Zweistichproben-t-Test?Ein Zweistichproben-t-Test vergleicht die Mittelwerte von zwei Gruppen, um festzustellen, ob sie signifikant unterschiedlich sind.
Wie formuliere ich Hypothesen?Die Nullhypothese (H_0) besagt, dass die Mittelwerte gleich sind, während die Alternativhypothese (H_1) besagt, dass sie unterschiedlich sind.
Wie berechne ich die Prüfgröße?Die Prüfgröße wird durch die Differenz der Mittelwerte geteilt durch die Wurzel der Summe der Varianzen berechnet.
Was mache ich nach der Berechnung?Vergleiche die Prüfgröße mit dem kritischen Wert, um zu entscheiden, ob du die Nullhypothese ablehnen kannst.
Warum ist die Standardabweichung wichtig?Die Standardabweichung hilft, die Variabilität der Daten zu verstehen, die für die Berechnung der Prüfgröße entscheidend ist.


