Zweistichproben-F-Test in Excel für Variablenvergleich

Statistische Tests sind ein unverzichtbarer Bestandteil der Datenanalyse, insbesondere wenn es darum geht, Unterschiede zwischen Gruppen zu prüfen. Ein bewährtes Verfahren, das häufig in der Forschung und Wirtschaft eingesetzt wird, ist der Zweistichproben-F-Test. Diese Anleitung zeigt dir Schritt für Schritt, wie du einen solchen Test mit Excel realisieren kannst, um die Variablen von zwei Pharmakonzerne bezüglich ihrer Forschungsausgaben zu vergleichen.

Wichtigste Erkenntnisse

• Du lernst, wie du die Varianz zweier Gruppen durch einen F-Test miteinander vergleichen kannst.
• Die Anleitung enthält detaillierte Schritte zur Durchführung des Tests in Excel, einschließlich der Verwendung der Datenanalyse-Funktion.
• Am Ende wirst du wissen, wie du die Ergebnisse interpretierst und welche Schlüsse daraus zu ziehen sind.

Schritt-für-Schritt-Anleitung

Schritt 1: Daten vorbereiten

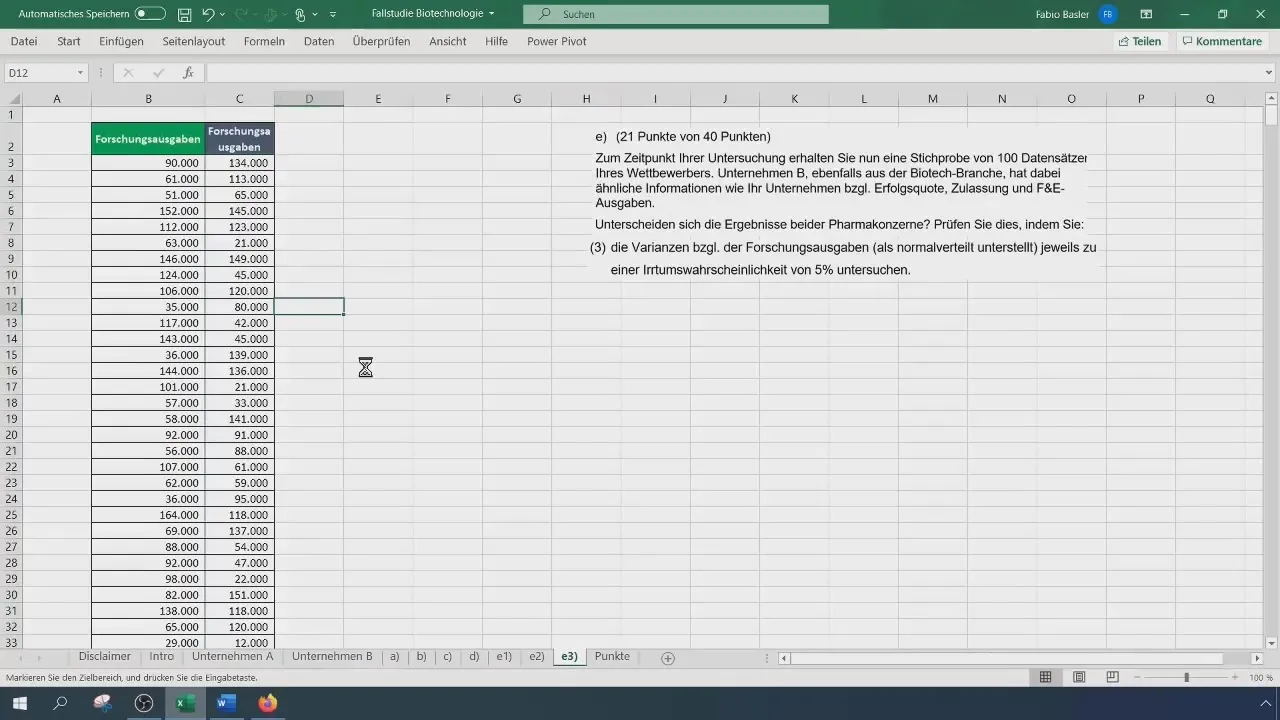
Zuerst benötigst du die Rohdaten der Forschungsausgaben der beiden Unternehmen. Öffne deine Excel-Datei und kopiere die jeweiligen Forschungsdaten der beiden Unternehmen in separate Spalten.

Schritt 2: Stichprobenumfang und Varianz berechnen

Ihre Stichprobengröße bleibt mit 500 für Unternehmen A und 100 für Unternehmen B gleich. Um die Varianz der Daten zu berechnen, verwendest du die Funktion VAR.S(), um die Varianz für die Gruppen zu schätzen. Achte darauf, die Werte im Excel-Format eingeben, um genaue Ergebnisse zu erzielen.

Schritt 3: Hypothesen formulieren

Für den F-Test sind die Hypothesen wie folgt festzulegen:

• Nullhypothese (H0): σ1² = σ2² (Die Varianzen der beiden Unternehmen sind gleich).
• Alternativhypothese (H1): σ1² ≠ σ2² (Die Varianzen der beiden Unternehmen sind ungleich).

Schritt 4: Prüfgröße berechnen

Berechne die Prüfgröße (F-Statistik) durch das Verhältnis der beiden Varianzen. Verwende die Formel Varianz_A / Varianz_B. Wenn du die Varianzen entsprechend imperialistisch eingegeben hast, erhältst du eine F-Statistik zum Vergleich.

Schritt 5: Kritischen Wert bestimmen

Um den kritischen F-Wert zu ermitteln, benötigst du das Alpha-Niveau (in der Regel 0,05) und die Freiheitsgrade. Freiheitsgrade berechnen sich wie folgt: df1 = n1 - 1 und df2 = n2 - 1. Berechne den kritischen Wert mit der Funktion F.INV().

Schritt 6: Entscheidung treffen

Vergleiche die ermittelte F-Statistik mit dem kritischen F-Wert. Wenn die F-Statistik größer als der kritische Wert ist, lehne die Nullhypothese ab, andernfalls nicht. In diesem Beispiel ist das Kriterium zur Ablehnung, dass die Prüfgröße kleiner als der quantiles Wert (F kritisch) sein muss.

Schritt 7: Excel Datenanalyse nutzen

Excel bietet auch die Möglichkeit, den F-Test über die Datenanalysefunktion durchzuführen. Gehe zu „Daten“ und wähle „Datenanalyse“. Wähle den „Zweistichproben-F-Test“ aus. Gebe die Bereiche der beiden Variablen ein und wähle die entsprechenden Einstellungen.

Schritt 8: Ergebnisse interpretieren

Analysiere die Ausgaben des F-Tests. Wenn die berechnete F-Statistik und der p-Wert in der Excel-Ausgabe die gleichen Ergebnisse liefern wie deine manuelle Berechnung, kannst du zu dem Schluss kommen, dass die Varianzen der beiden Unternehmen gleich sind.

Zusammenfassung

Der Zweistichproben-F-Test ist ein essenzielles Werkzeug in der statistischen Analyse, das es dir ermöglicht, Unterschiede in der Varianz von zwei Gruppen zu vergleichen. In dieser Anleitung hast du gelernt, wie du diesen Test effektiv in Excel durchführst, von der Datenvorbereitung bis hin zur Interpretation der Ergebnisse.