Chi-Quadrat-Anpassungstest auf Normalverteilung mit Excel

Der Chi-Quadrat-Anpassungstest stellt eine einfache Methode dar, um die Hypothese zu überprüfen, ob eine gegebene Datenreihe einer Normalverteilung folgt. In dieser Anleitung wirst du lernen, wie du den Chi-Quadrat-Test in Excel durchführen kannst, um festzustellen, ob die Umsätze von Smartphones einer Normalverteilung entsprechen. Wir werden Schritt für Schritt durch den Prozess gehen, der von der Erstellung einer klassierten Häufigkeitstabelle bis zur Berechnung der Prüfgröße und dem Vergleich mit dem kritischen Wert des Chi-Quadrats reicht.

Wichtigste Erkenntnisse

• Der Chi-Quadrat-Anpassungstest hilft bei der Prüfung von Normalverteilungen.
• Es ist wichtig, eine klassierte Häufigkeitstabelle zu erstellen.
• Die Prüfgröße wird mit einem kritischen Wert verglichen, um die Nullhypothese abzulehnen oder zu akzeptieren.

Schritt-für-Schritt-Anleitung

Schritt 1: Daten vorbereiten

Um den Chi-Quadrat-Test durchzuführen, benötigst du zunächst die Daten. Kopiere die Umsätze der Smartphones in ein Excel-Arbeitsblatt. Stelle sicher, dass deine Daten in einer einzelnen Spalte organisiert sind.

Schritt 2: Histogramm erstellen

Um erste visuelle Hinweise auf die Verteilung zu erhalten, erstelle ein Histogramm deiner Daten. Gehe dazu zu „Einfügen“ und wähle „Diagramme“. Füge ein Histogramm hinzu, indem du den Bereich für die Daten auswählst.

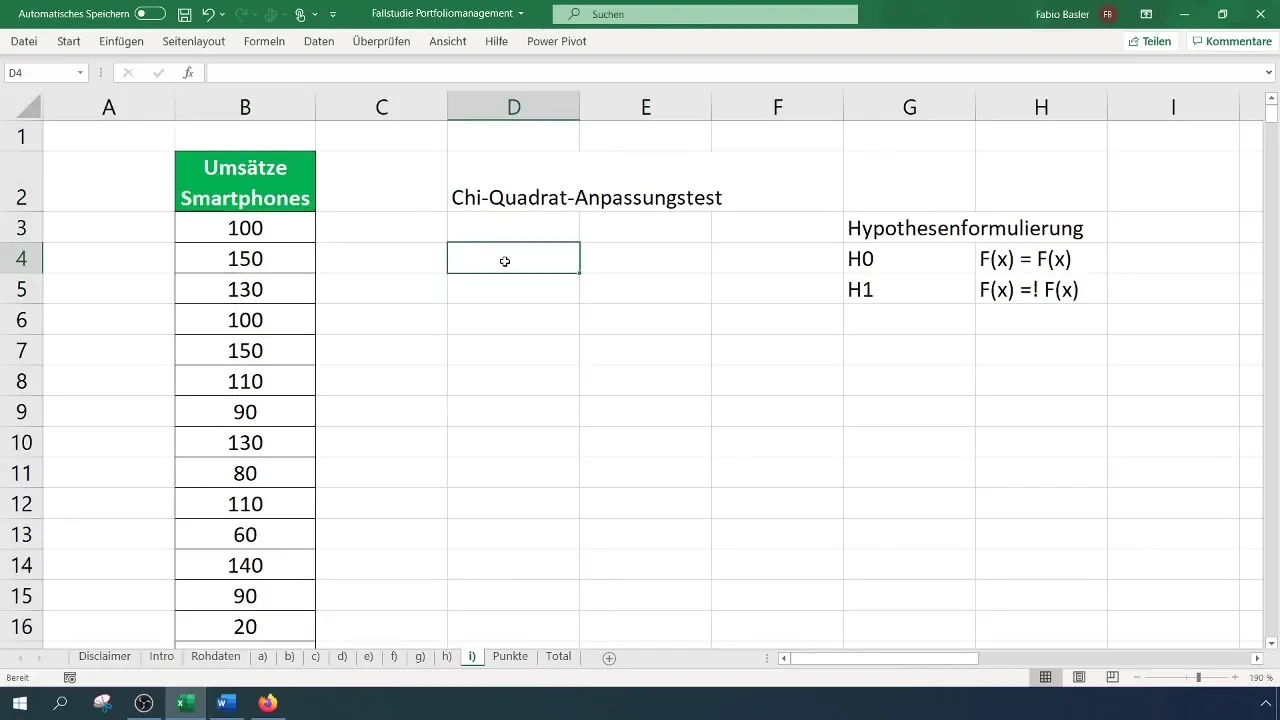
Schritt 3: Klassierte Häufigkeitstabelle erstellen

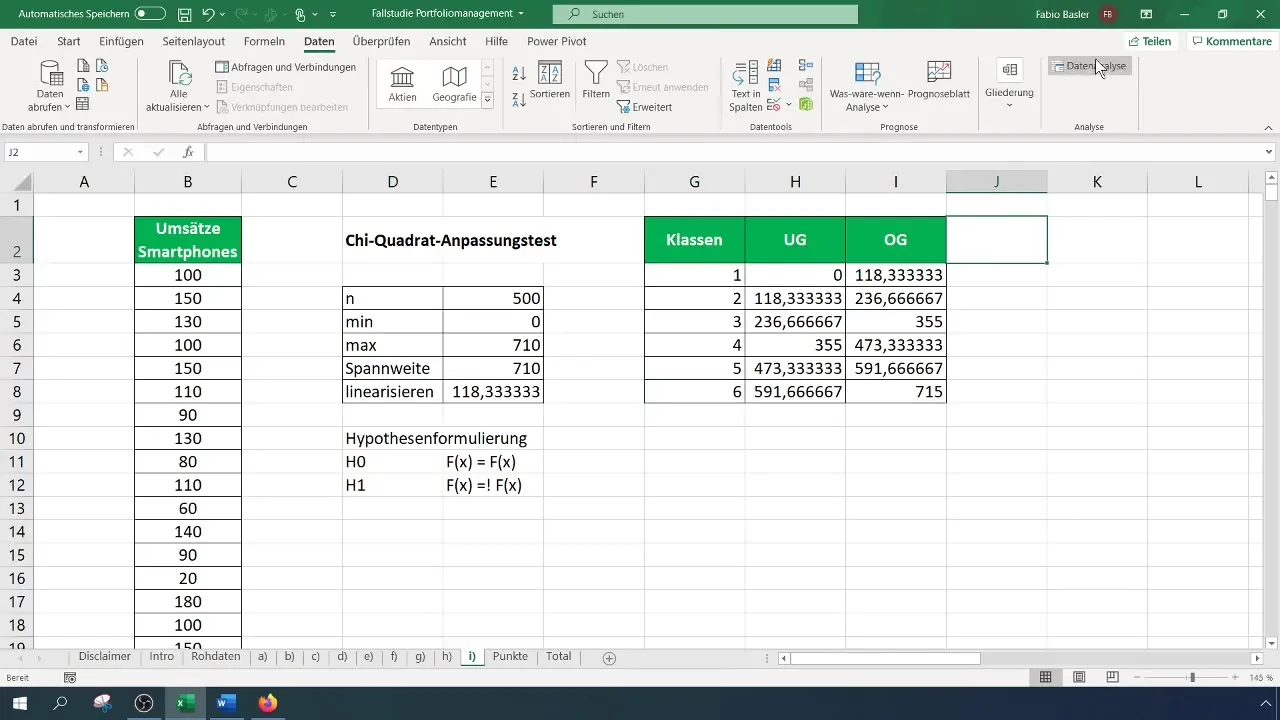
Für den Chi-Quadrat-Test brauchst du eine klassierte Häufigkeitstabelle. Bestimme zunächst die Anzahl der Klassen für deine Tabelle – in diesem Fall nutzen wir sechs Klassen. Berechne die Breite der Intervalle und erstelle die Tabelle entsprechend.

Schritt 4: Frequenzen berechnen

Jetzt musst du die beobachteten Frequenzen für jede Klasse berechnen. Gehe zu „Datenanalyse“ aus dem Menü und wähle „Histogramm“. Wähle den Eingabebereich für deine Daten und die Klassengrenzen aus. Bestimme den Ausgabebereich für die Häufigkeitstabelle.

Schritt 5: Erwartete Frequenzen berechnen

Um die erwarteten Frequenzen zu ermitteln, berechne die Wahrscheinlichkeiten für jede Klasse basierend auf der angenommenen Normalverteilung. Hierfür benötigst du den Mittelwert und die Standardabweichung deiner Daten.

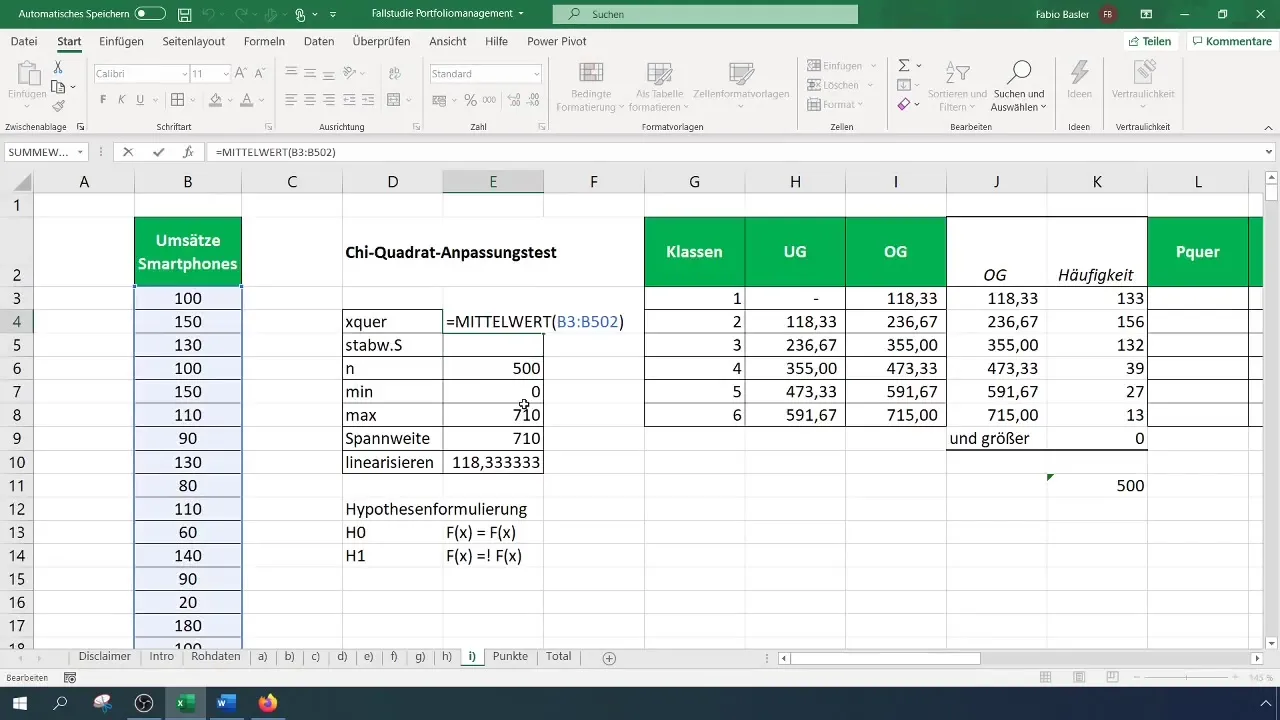
Schritt 6: Prüfgröße berechnen

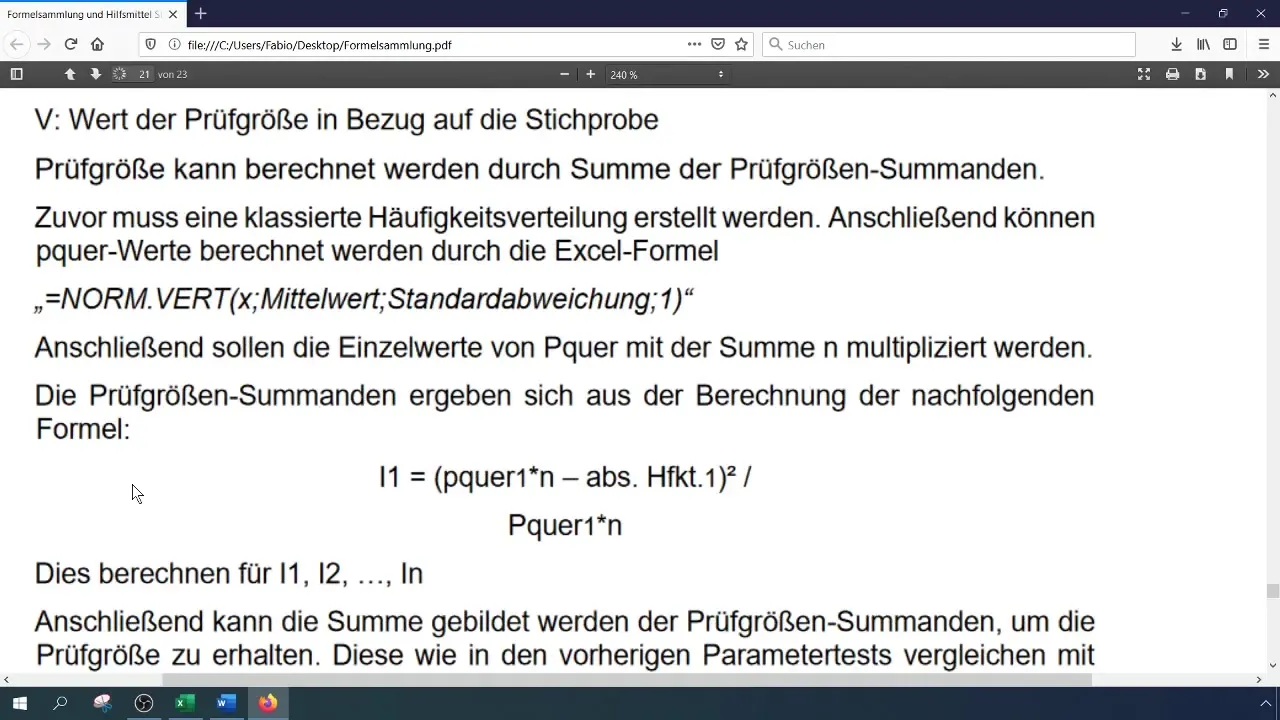
Berechne die Prüfgröße (Chi-Quadrat) mit der Formel:

[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]

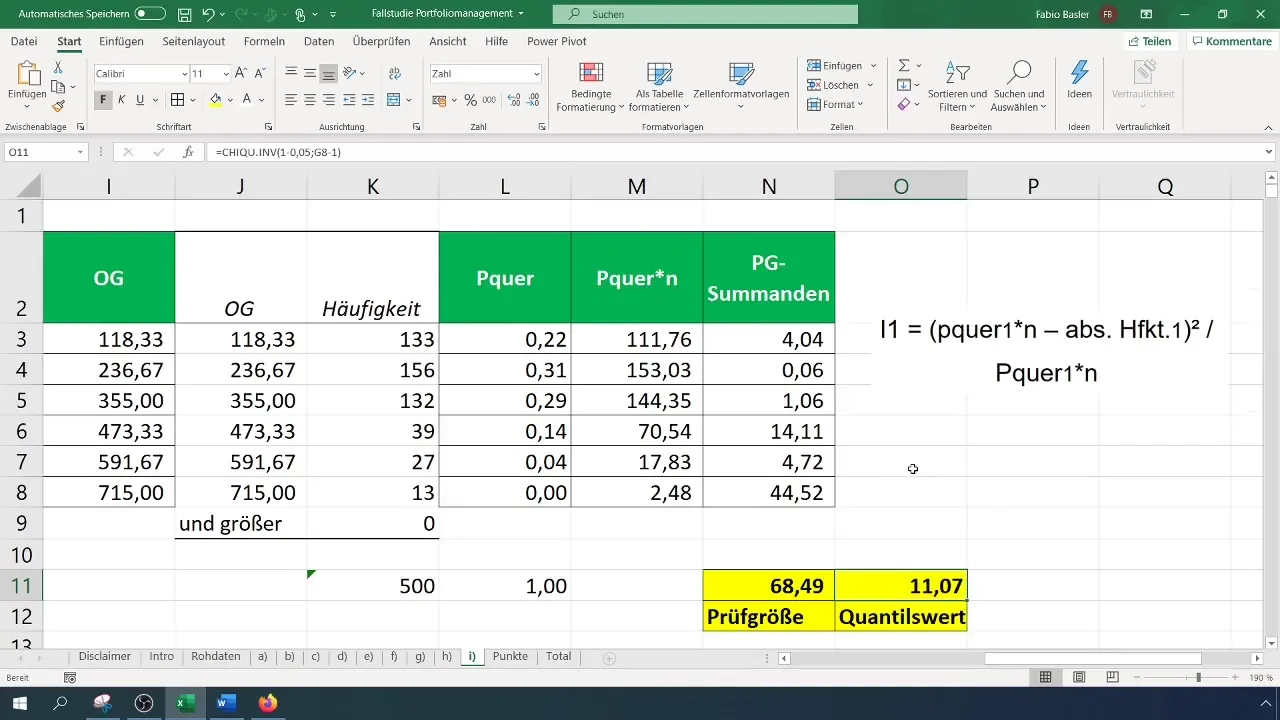
wobei (O_i) die beobachteten und (E_i) die erwarteten Häufigkeiten sind. Du kannst diese Berechnung in Excel durchführen, indem du die einzelnen Komponenten in separaten Zellen speicherst.

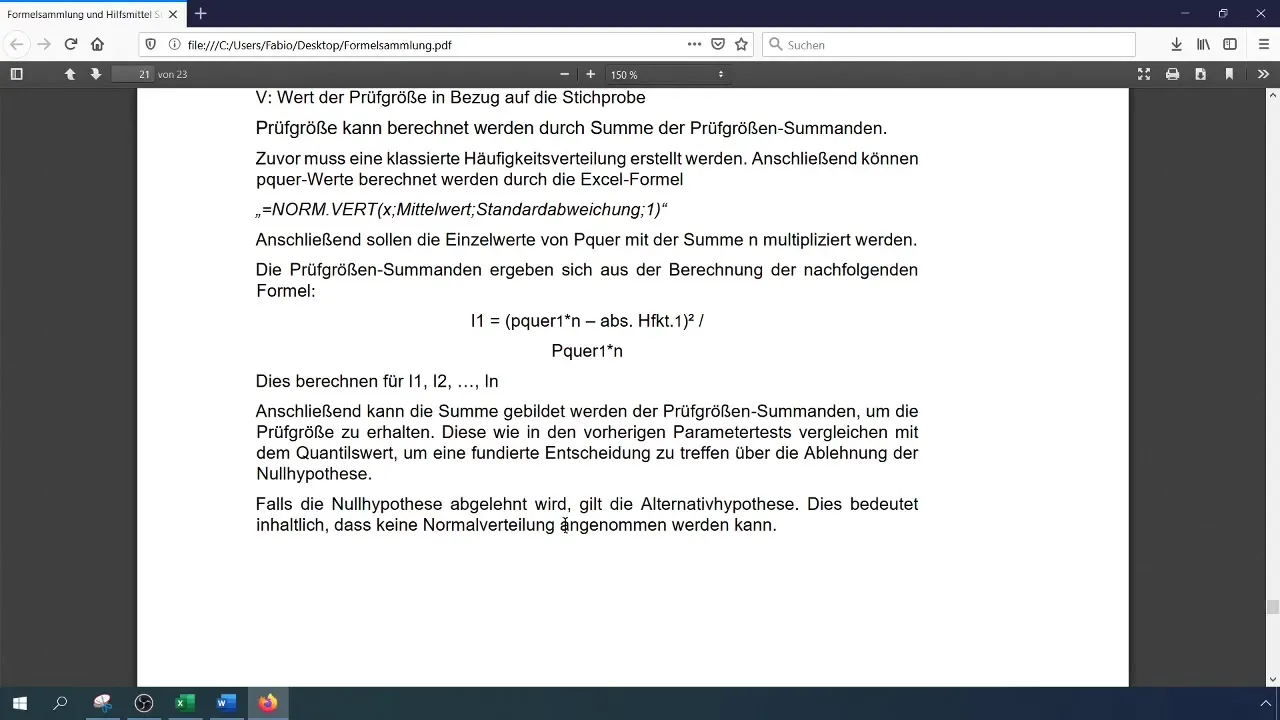
Schritt 7: Kritischen Wert berechnen

Um die Prüfgröße zu bewerten, musst du den kritischen Wert ( \chi^2 ) für dein Konfidenzniveau und die Anzahl der Freiheitsgrade berechnen. Die Anzahl der Freiheitsgrade für den Chi-Quadrat-Test ist (k - 1), wobei (k) die Anzahl der Klassen ist.

Schritt 8: Hypothesen überprüfen

Vergleiche deine berechnete Prüfgröße mit dem kritischen Wert. Wenn die Prüfgröße größer ist als der kritische Wert, lehne die Nullhypothese ab, was bedeutet, dass die Daten nicht normalverteilt sind. Andernfalls akzeptierst du die Nullhypothese.

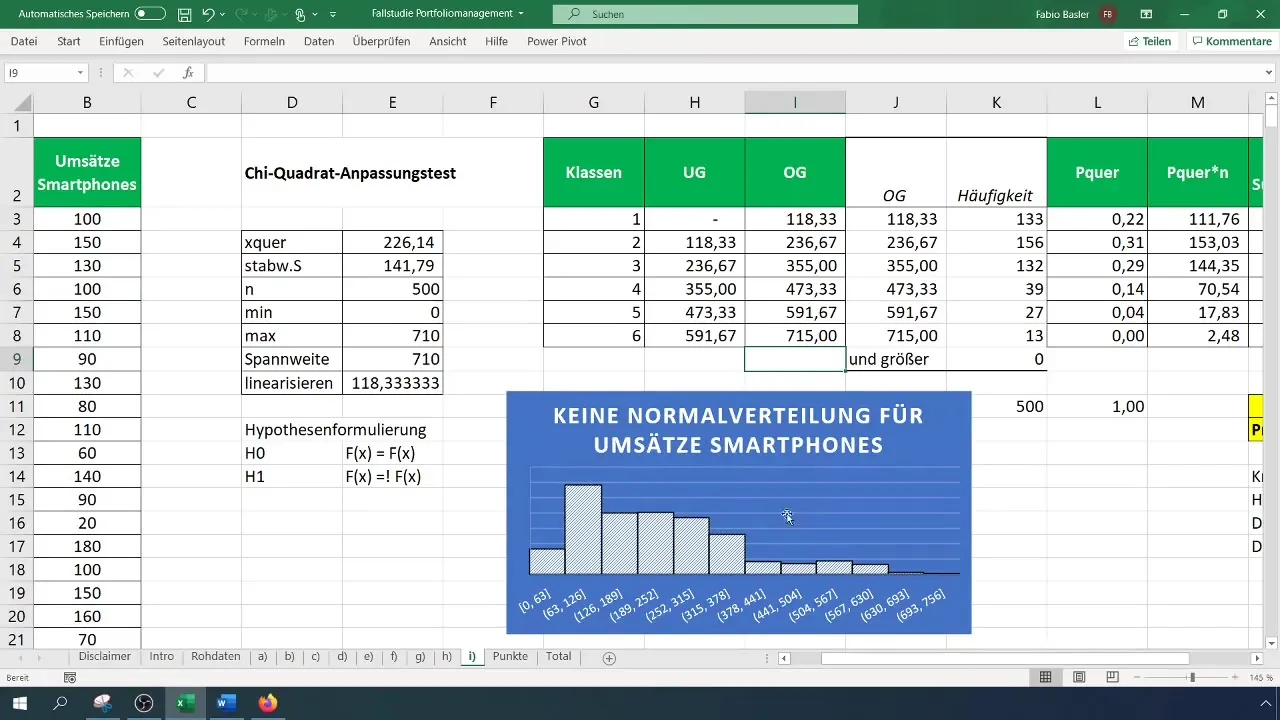
Schritt 9: Ergebnisse zusammenfassen

Halte deine Ergebnisse fest, und erweitere sie um die grafischen Daten und die Hypothesentests. Vergiss nicht, dein Histogramm zu überprüfen, um visuell zu bestätigen, dass die Verteilung nicht normal ist.

Zusammenfassung

Im Verlauf dieser Anleitung hast du gelernt, wie du den Chi-Quadrat-Anpassungstest in Excel ausführst, um die Normalverteilung deiner Smartphone-Umsätze zu analysieren. Die Schritte beinhalten das Erstellen einer klassierten Häufigkeitstabelle, Berechnungen für die erwarteten Frequenzen, die Prüfgröße und schließlich den Vergleich dieser mit dem kritischen Wert.