Statistische Analysen sind ein unerlässliches Werkzeug im Portfoliomanagement. Ein besonders mächtiges Verfahren ist die Regressionsanalyse, insbesondere wenn es darum geht, den Einfluss mehrerer unabhängiger Variablen auf eine abhängige Variable zu bestimmen. Du willst erfahren, wie du in Excel einen linearen Funktionszusammenhang durch eine multiple Regression aufbauen und analysieren kannst? Diese Anleitung bietet dir einen klaren Überblick sowie eine detaillierte Schritt-für-Schritt-Anleitung.
Wichtigste Erkenntnisse
- Die Regressionsanalyse hilft, den Einfluss von unabhängigen Variablen auf eine abhängige Variable zu quantifizieren.
- Es ist wichtig, die Güte und die statistische Signifikanz des Regressionsmodells zu bewerten.
- Durch die Einschätzung der Koeffizienten kann festgestellt werden, welche unabhängige Variable den stärkeren Einfluss auf die abhängige Variable hat.
Schritt-für-Schritt-Anleitung zur Regressionsanalyse in Excel
Vorbereitung der Daten
Bevor du mit der Regressionsanalyse beginnen kannst, musst du deine Daten aufbereiten. Die abhängige Variable (y) ist in diesem Fall der Umsatz der Notebooks, und die unabhängigen Variablen (x1 und x2) sind die Anzahl der Mitarbeiter und die Anzahl der Konkurrenzaktionen. Zuerst solltest du alle benötigten Daten in Excel eingeben und sie übersichtlich strukturieren.
Korrelation überprüfen
Um erste Hinweise auf mögliche Zusammenhänge zwischen den Variablen zu erhalten, kannst du eine Korrelationsmatrix erstellen. Diese Matrix hilft dir zu sehen, wie stark die unterschiedlichen Variablen miteinander verbunden sind. Du kannst dies über die Funktion „Datenanalyse“ in Excel tun und dann die Korrelationsmatrix auswählen, wobei du alle relevanten Datenbereiche einbeziehen solltest.
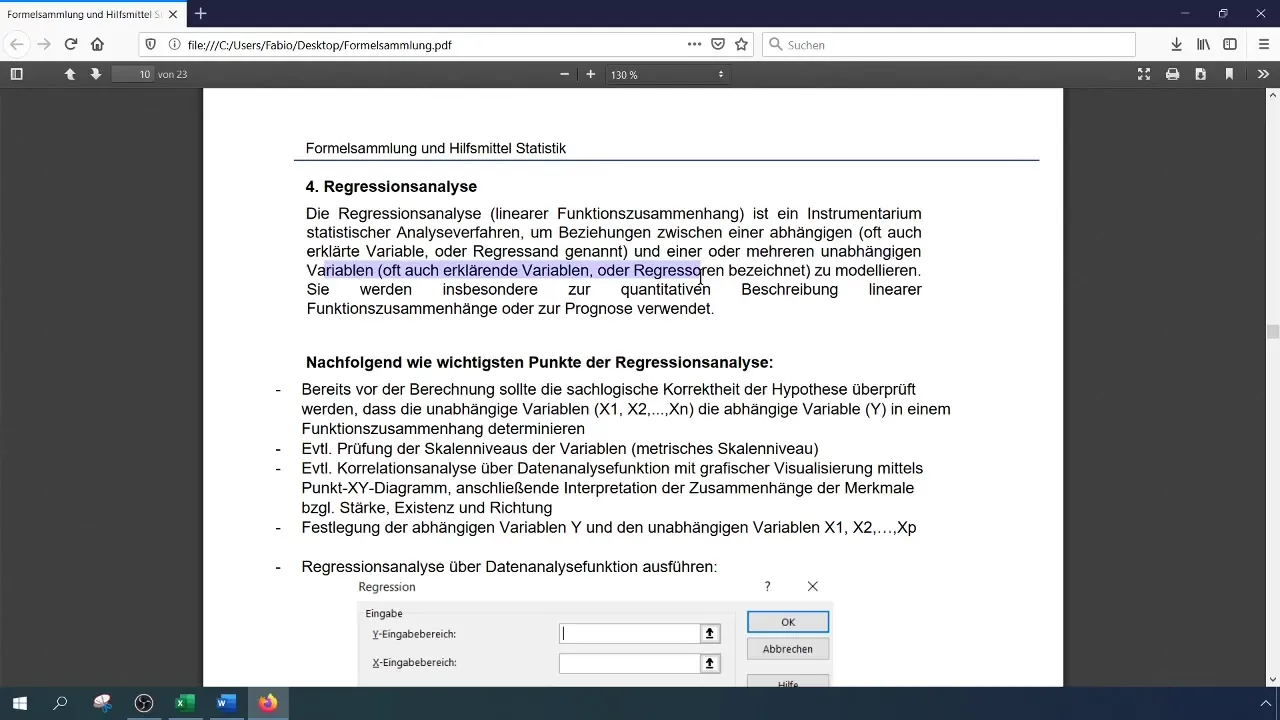
Durchführung der Regressionsanalyse
Jetzt bist du bereit, die Regressionsanalyse auszuführen. Wähle dazu erneut die Funktion „Datenanalyse“, dann wähle „Regression“. Hier gibst du den Eingabebereich für die abhängige Variable (Umsatz der Notebooks) und die unabhängigen Variablen (Anzahl der Mitarbeiter und Konkurrenzaktionen) an.
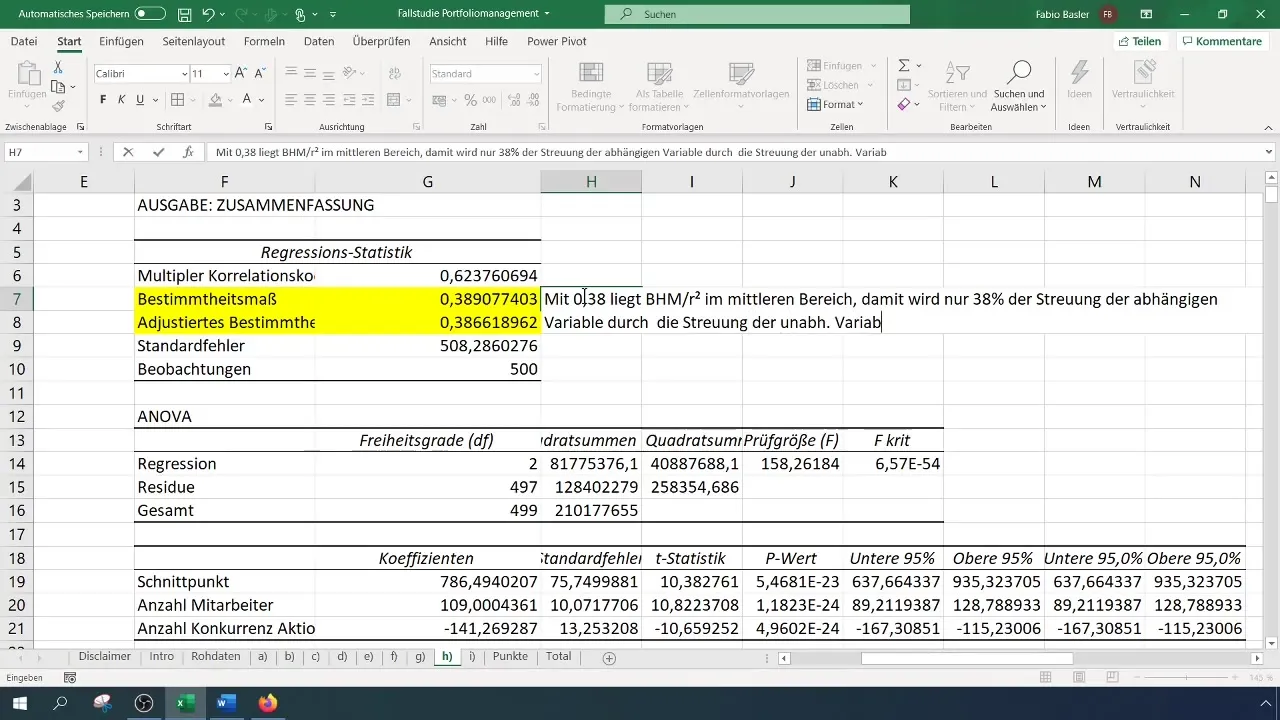
Interpretation der Ergebnisse
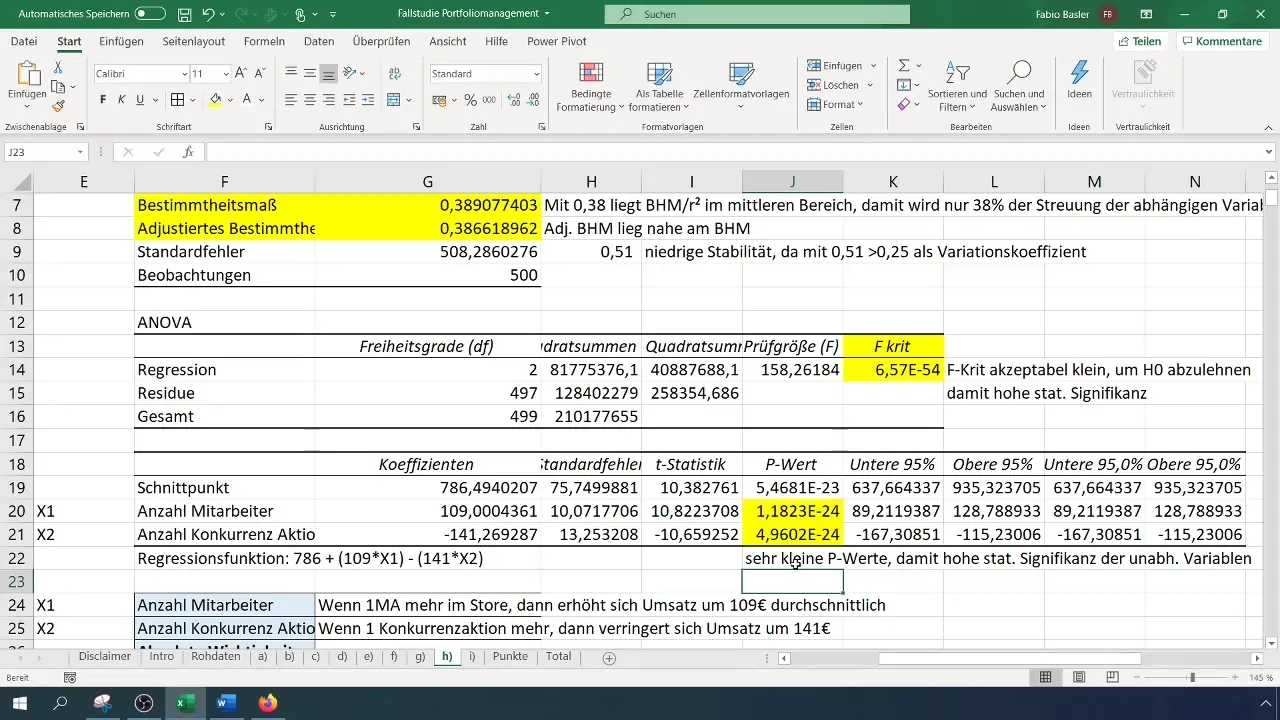
Nach Durchführung der Regressionsanalyse erhältst du eine Vielzahl von Ausgaben und Statistiken. Der erste wichtige Punkt ist das Bestimmtheitsmaß (R²), welches den Anteil der Erklärung der abhängigen Variablen durch die unabhängigen Variablen beschreibt. Ein R²-Wert von 0,38 weist darauf hin, dass 38% der Variabilität im Umsatz durch die beiden unabhängigen Variablen erklärt werden können.
In der Auswertung solltest du darauf achten, wie stabil das Modell ist. Hierbei kannst du den Standardfehler zur Ermittlung der Stabilität heranziehen. Wenn du beispielsweise einen Standardfehler von 0,51 erhältst, bedeutet dies eine hohe relative Schwankung und damit eine niedrige Stabilität.
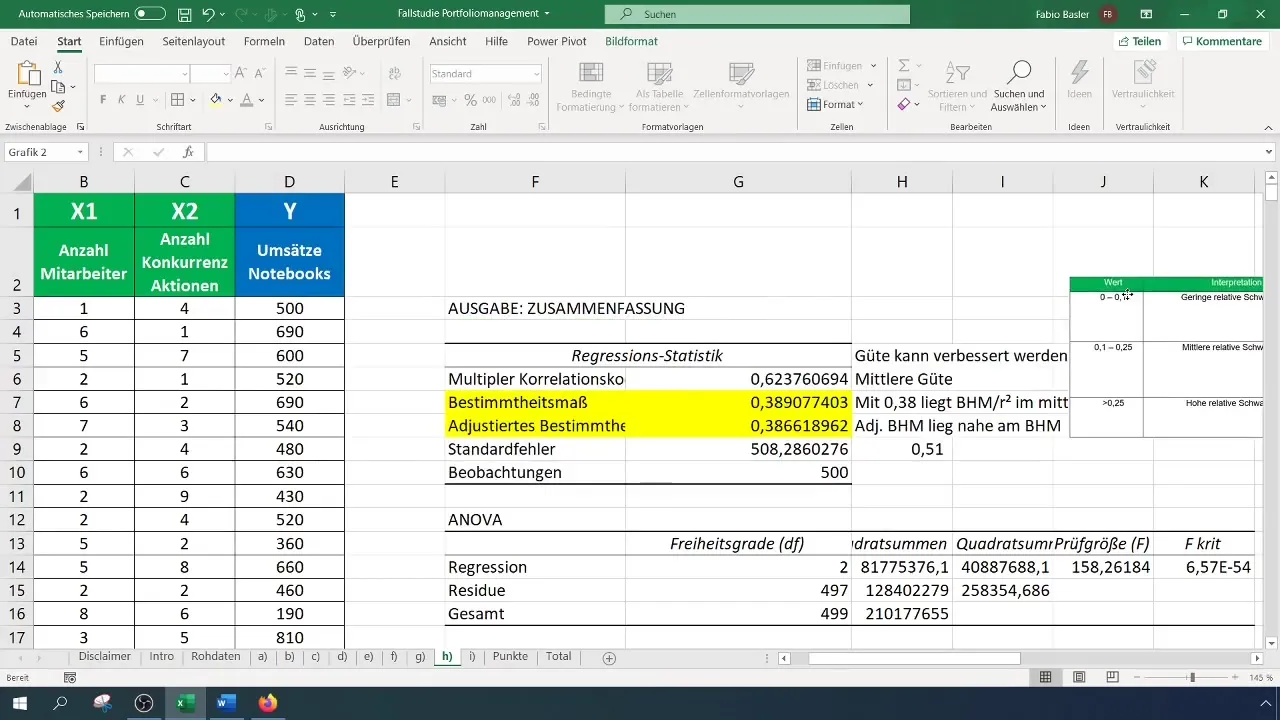
Bewertung der starken Einflussfaktoren
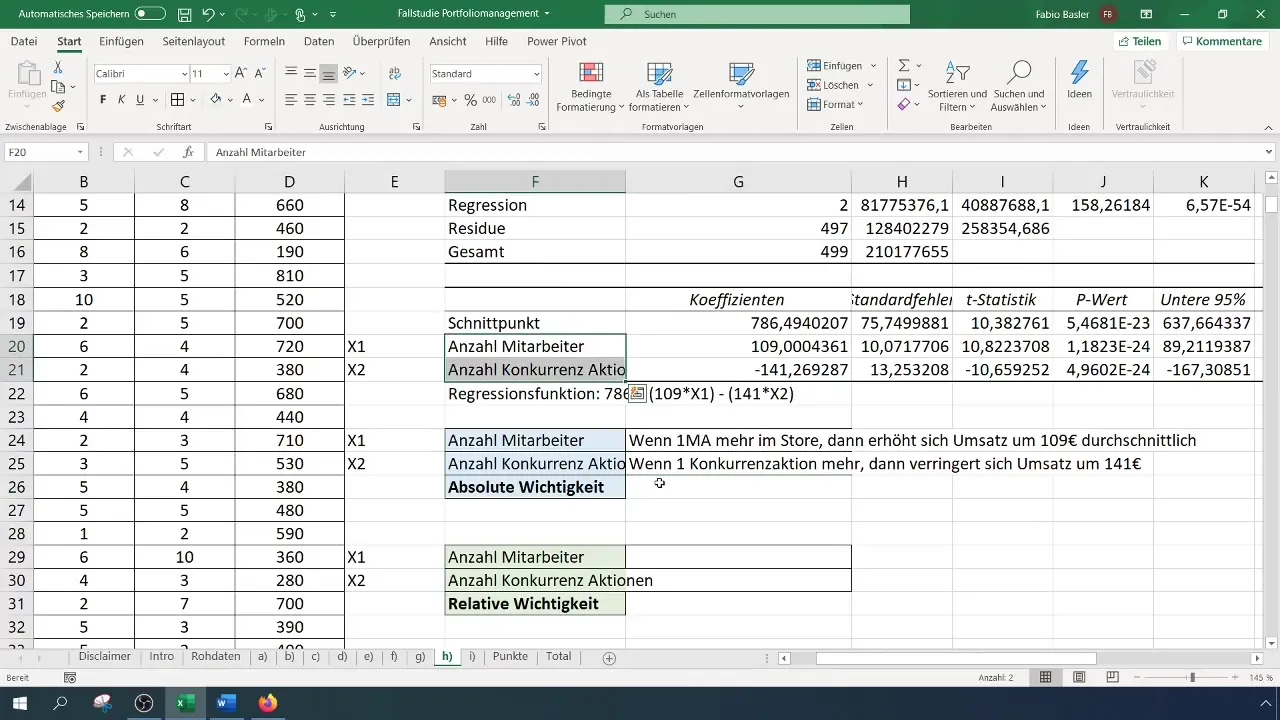
Ein entscheidender Schritt ist, herauszufinden, welche der unabhängigen Variablen einen stärkeren Einfluss auf die abhängige Variable hat. Dies kannst du mithilfe der Koeffizienten tun, die die absolute Relevanz der Variablen angeben. Hierbei ist der Koeffizient von x1 (Anzahl Mitarbeiter) 109, während der Koeffizient von x2 (Anzahl Konkurrenzaktionen) -141 ist. Dies sagt aus, dass jede Erhöhung der Anzahl der Mitarbeiter den Umsatz um 109 Euro steigert, während jede Erhöhung der Konkurrenzaktionen den Umsatz um 141 Euro reduziert.
Bewertung der statistischen Signifikanz
Ein weiterer wichtiger Aspekt der Regressionsanalyse ist die statistische Signifikanz. Du kannst dies an den p-Werten und dem F-Test ablesen, die beide sehr kleine Werte aufweisen sollten. Dies zeigt, dass die unabhängigen Variablen einen signifikanten Einfluss auf die abhängige Variable haben, und es rechtfertigt die Verwendung des Modells.
Zusammenfassung
Die Regressionsanalyse in Excel ermöglicht es dir, den Zusammenhang zwischen verschiedenen Variablen quantitativ zu erfassen. Mit dieser Anleitung hast du die Schritte zur Durchführung und Interpretation einer multiplen Regression kennengelernt. Achte darauf, die Güte und Stabilität des Modells sowie die einzelnen Einflussfaktoren kritisch zu bewerten, um fundierte Entscheidungen im Portfoliomanagement zu treffen.
Häufig gestellte Fragen
Welche Daten benötige ich für die Regressionsanalyse?Du benötigst eine abhängige Variable (z.B. Umsatz) und mindestens eine oder mehrere unabhängige Variablen (z.B. Anzahl Mitarbeiter, Konkurrenzaktionen).
Wie interpretiere ich das Bestimmtheitsmaß R²?Ein höherer R²-Wert bedeutet, dass ein größerer Anteil der Variabilität in der abhängigen Variablen durch die unabhängigen Variablen erklärt wird.
Wie kann ich die statistische Signifikanz prüfen?Du kannst die p-Werte und den F-Test heranziehen; niedrige Werte deuten auf eine hohe Signifikanz hin.
Was ist der Unterschied zwischen R² und dem adjustierten R²?Der adjustierte R² berücksichtigt die Anzahl der unabhängigen Variablen und bietet eine realistischere Einschätzung bei Modellen mit mehreren Variablen.
Wie kann ich die Stärke der Einflussfaktoren einschätzen?Dies erfolgt durch die Betrachtung der Koeffizienten der unabhängigen Variablen, die den Einfluss jeder Variable auf die abhängige Variable quantifizieren.


