Berechnung des zweiseitigen Konfidenzintervalls in Excel

Es ist entscheidend, fundierte Entscheidungen im Business- und Vertriebsumfeld auf Basis von Datenanalysen zu treffen. Ein zweiseitiges Konfidenzintervall ermöglicht es dir, den Bereich zu bestimmen, in dem der wahre Durchschnittswert eines Parameters mit einer bestimmten Wahrscheinlichkeit zu finden ist. In dieser Anleitung zeige ich dir, wie du mithilfe von Excel den Bereich der Intervallgrenzen für den Wochenumsatz eines Vertriebsteams bei einer Vertrauenswahrscheinlichkeit von 93 % berechnen kannst.

Wichtigste Erkenntnisse

Zu den wesentlichen Aspekten des zweiseitigen Konfidenzintervalls gehören:

1. Die Berechnung des Mittelwerts als Schätzwert für den Parameter.
2. Bestimmung der Standardabweichung aus der Stichprobe.
3. Anwendung der Formeln zur Ermittlung der Unter- und Obergrenzen des Intervalls.
4. Berücksichtigung der Vertrauenswahrscheinlichkeit zur Situierung des Intervalls.

Schritt-für-Schritt-Anleitung

Zunächst benötigen wir ein solides Verständnis der Begrifflichkeiten und Schritte, die diesen Prozess umreißen.

Schritt 1: Datenvorbereitung

Zuerst solltest du die Daten für das Vertriebsteam A aufbereiten. Filtere die relevanten Daten entsprechend und kopiere sie in dein Excel-Dokument.

Schritt 2: Berechnung des Mittelwerts

Um das Konfidenzintervall zu berechnen, ist der erste Schritt die Ermittlung des Mittelwerts, der als Schätzwert für den erwarteten Umsatz dient. In Excel kannst du dies mit der Formel =MITTELWERT(Bereich) tun, wobei „Bereich“ die Zelle(n) ist/sind, die die Daten für den Wochenumsatz des Vertriebsteams A enthalten.

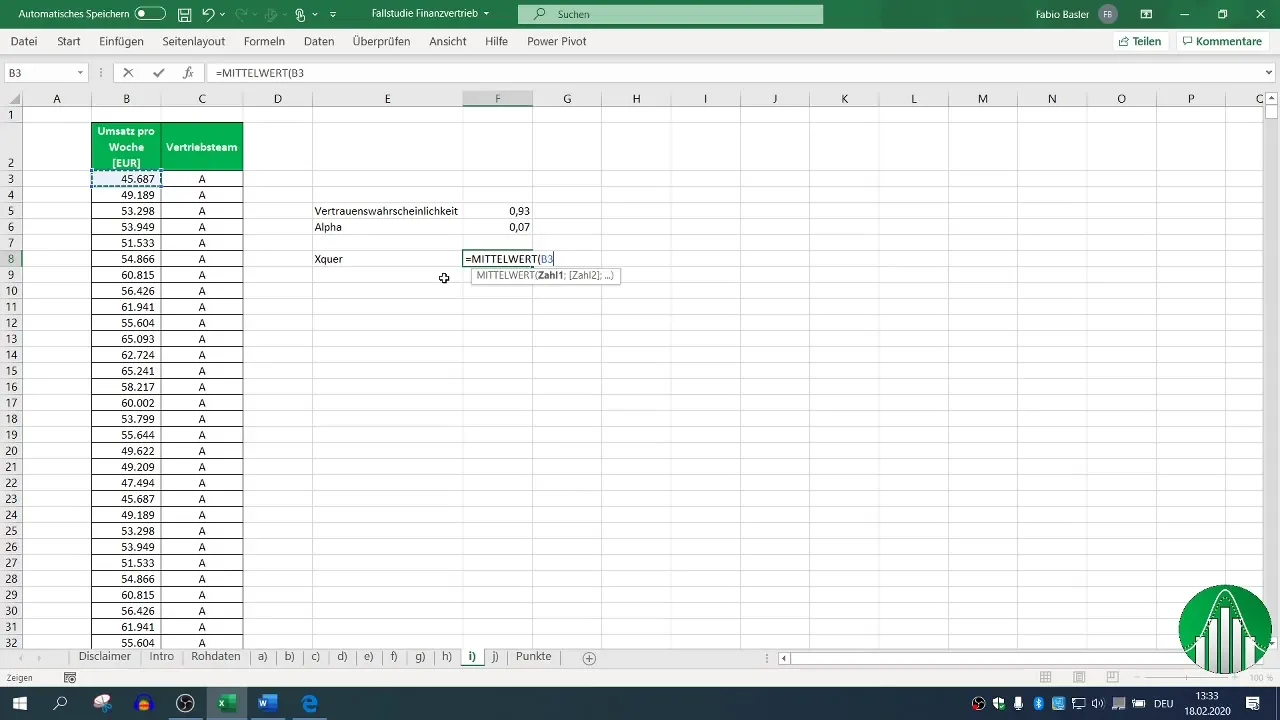
Schritt 3: Berechnung der Standardabweichung

Die Standardabweichung (σ) ist für die Berechnung des zweiseitigen Konfidenzintervalls von Bedeutung. Du kannst sie in Excel mit der Formel =STABW.S(Bereich) berechnen. Stelle sicher, dass du die passende Formel für die Standardabweichung der Stichprobe wählst.

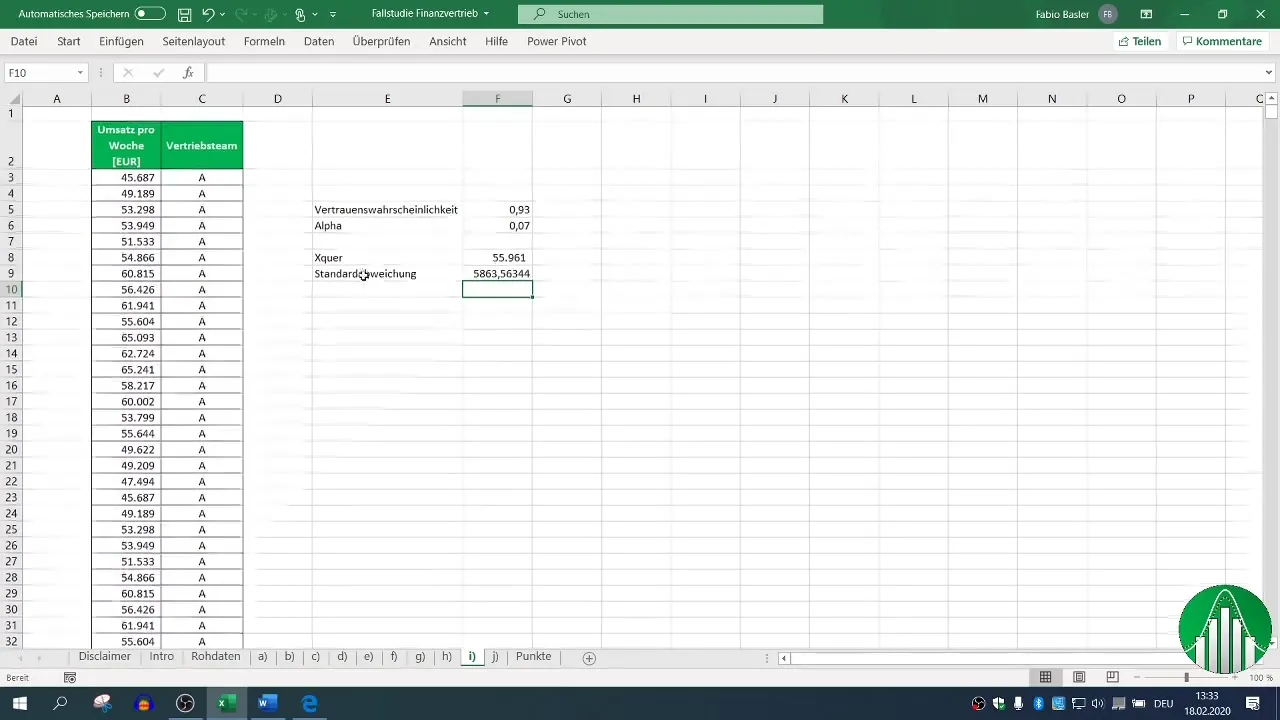
Schritt 4: Bestimmen des Stichprobenumfangs

Anschließend musst du den Stichprobenumfang (n) ermitteln. Addiere die Anzahl der Datensätze, die du für das Vertriebsteam A gesammelt hast. In diesem Beispiel gehen wir von 33 Datensätzen aus.

Schritt 5: Berechnung der Standardabweichung des Mittelwerts (σ_m)

Für die Berechnung des Konfidenzintervalls ist es notwendig, die Standardabweichung des Mittelwerts zu berechnen, die einfach die Standardabweichung geteilt durch die Quadratwurzel des Stichprobenumfangs ist.

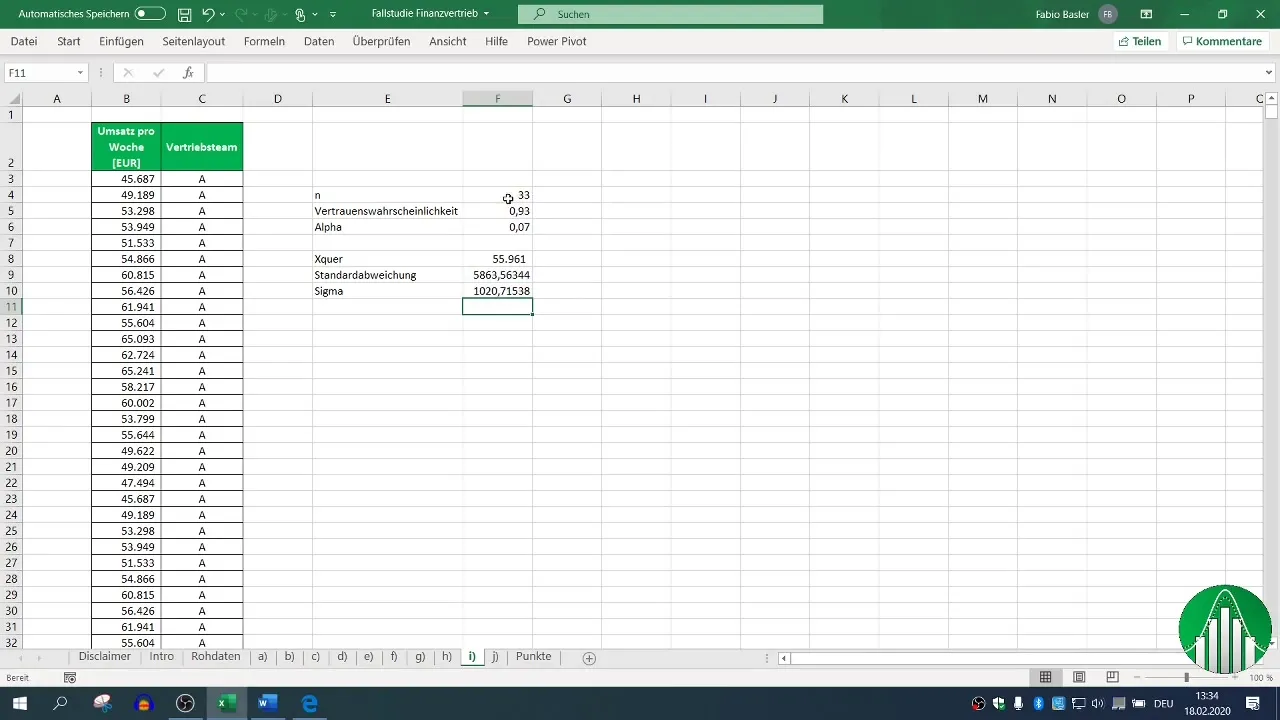
Schritt 6: Bestimmen des Quantils

Für die Berechnung des zweiseitigen Konfidenzintervalls benötigst du das Quantil. Da du eine Vertrauenswahrscheinlichkeit von 93 % angibst, liegt α bei 7 % und die Verteilung des Quantils findest du durch die Verwendung der Excel-Funktion.

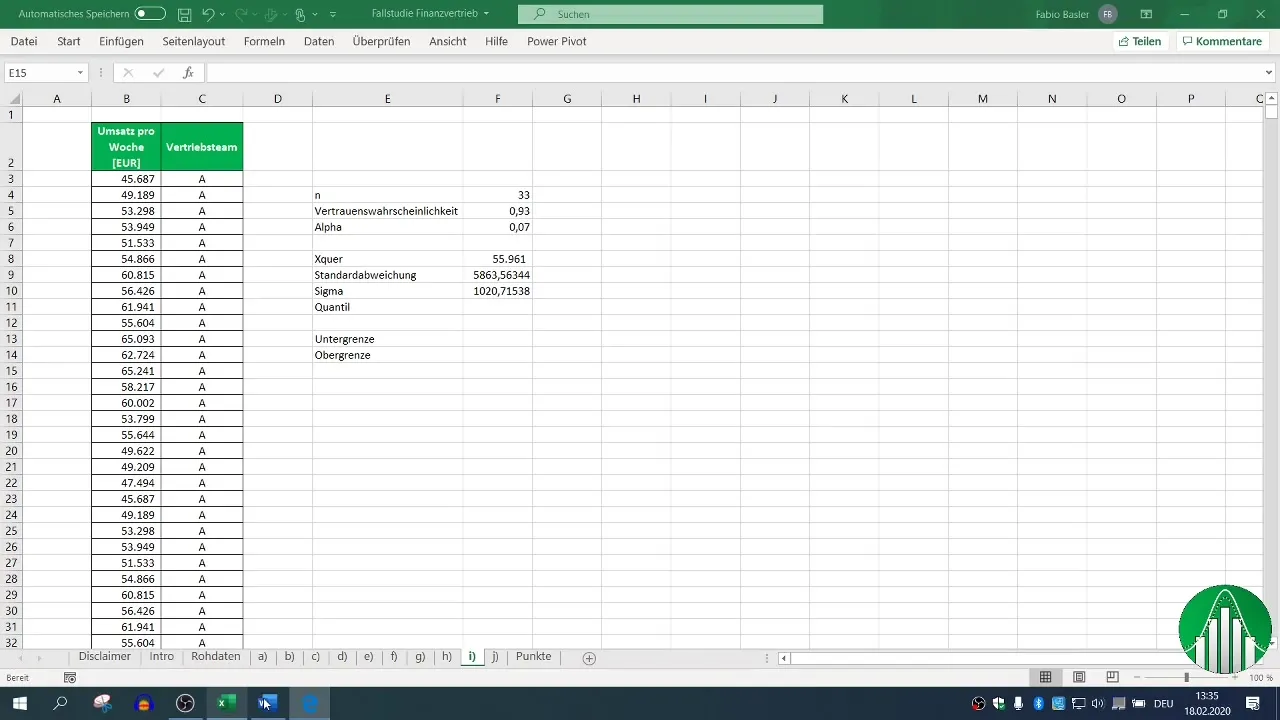
Schritt 7: Berechnung der Untergrenze

Jetzt berechnen wir die Untergrenze des Konfidenzintervalls. Dafür ziehst du von dem Mittelwert (x̄) das Produkt aus dem Quantil und der Standardabweichung des Mittelwerts ab.

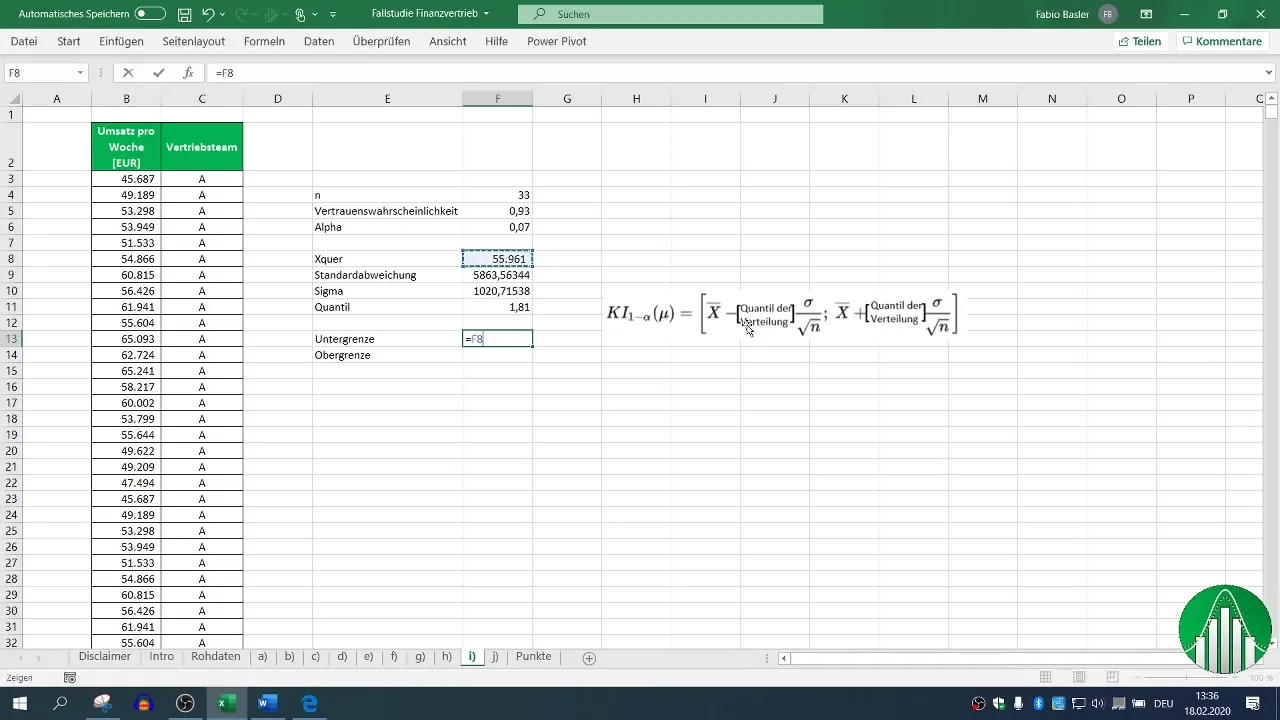
Schritt 8: Berechnung der Obergrenze

Die Obergrenze wird ähnlich berechnet, aber du addierst das Produkt statt zu subtrahieren.

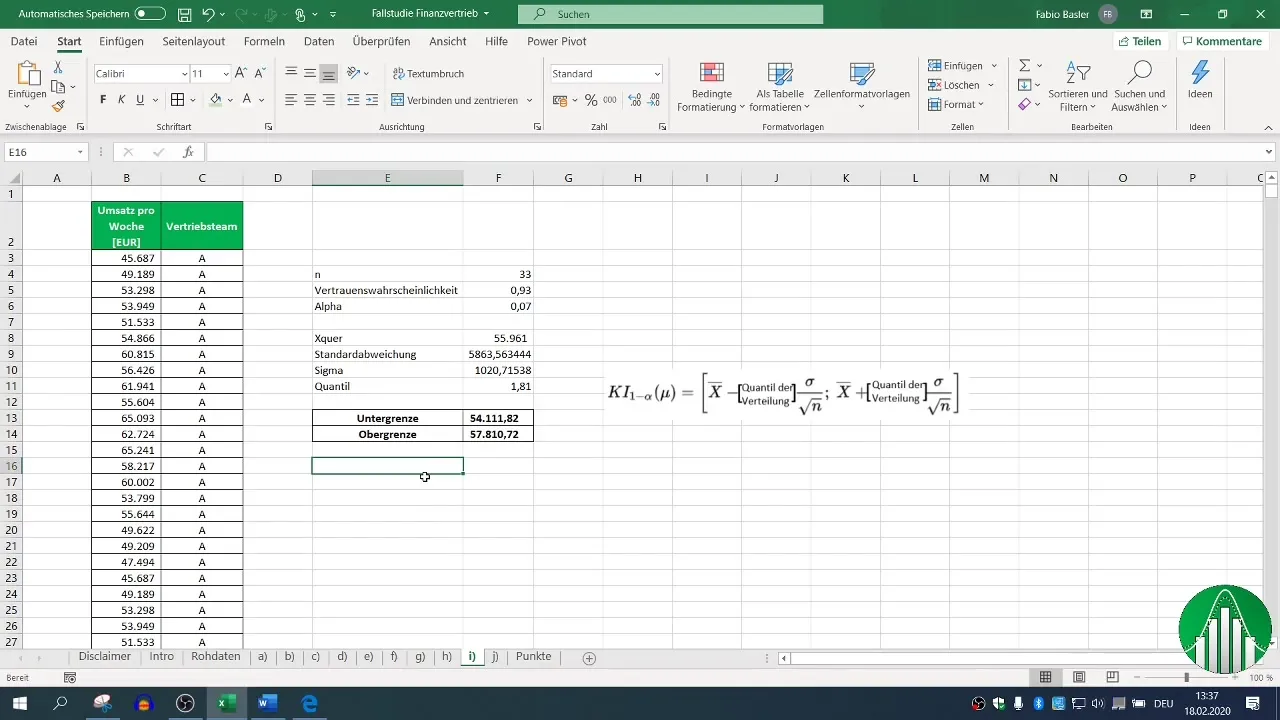
Schritt 9: Ergebnisinterpretation

Nach diesen Berechnungen erhältst du das zweiseitige Konfidenzintervall für den Wochenumsatz des Vertriebsteams A. In unserem Beispiel liegt das Intervall zwischen 54,111 und 57,810. Dies bedeutet, dass mit einer Vertrauenswahrscheinlichkeit von 93 % der wahre durchschnittliche Umsatzwert in diesem Bereich liegt.

Zusammenfassung

Durch die exakte Berechnung des zweiseitigen Konfidenzintervalls kannst du präzise Aussagen über den zukünftigen Umsatz treffen. Du hast gelernt, wie du die relevanten Daten aufbereiten, den Mittelwert und die Standardabweichung berechnen und schließlich die Grenzen des Intervalls ermitteln kannst. Mit dieser Methode kannst du datengestützte Entscheidungen in deinem Vertriebsbereich treffen.