Rangkorrelationsanalysen sind in der statistischen Untersuchung von Beziehungen zwischen Variablen von zentraler Bedeutung. Insbesondere, wenn es um ordinal skalierte Daten geht, ist die Spearman-Rangkorrelation eine wertvolle Methode, um Muster und Verbindungen zu erkennen. In dieser Anleitung erfährst du Schritt für Schritt, wie du die Rangkorrelation nach Spearman für eine Umfrage mit Hilfe von Excel berechnen kannst.
Wichtigste Erkenntnisse
- Rangkorrelation misst die Stärke und Richtung einer monotonen Beziehung zwischen zwei ordinalen Variablen.
- Der Spearman-Rangkorrelationskoeffizient ist besonders geeignet, wenn eine der Variablen ordinal und die andere metrisch skaliert ist.
- Die Berechnung in Excel kann mithilfe einfacher Formeln und Funktionen erfolgen.
Schritt-für-Schritt-Anleitung
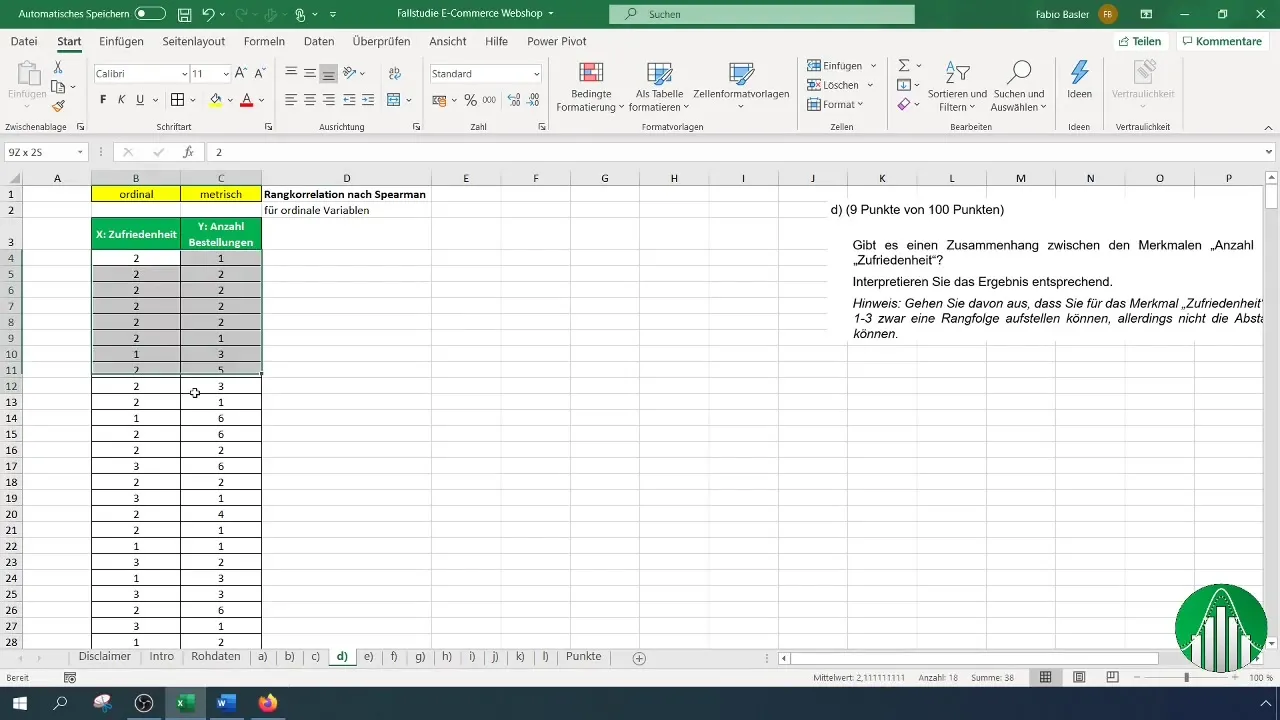
Zunächst definieren wir die Variablen, die wir analysieren möchten. In diesem Fall handelt es sich um die Zufriedenheit der Kunden (ordinal skaliert, Werte 1-3) und die Anzahl der Bestellungen (metrisch skaliert).
Um eine Rangordnung für die Zufriedenheit und die Anzahl der Bestellungen zu erstellen, benötigst du eine Tabelle, die die entsprechenden Daten enthält. Stelle sicher, dass du diese Daten in Excel eingibst.

Nachdem du deine Daten in Excel eingegeben hast, betrachten wir die Berechnung der Rangkorrelation nach Spearman. Hierfür verwenden wir die Funktion „Rang.Mittel“ in Excel, die den Rang einer Zahl innerhalb einer Liste zurückgibt. Für die Zufriedenheit benutzen wir zunächst die Formel:
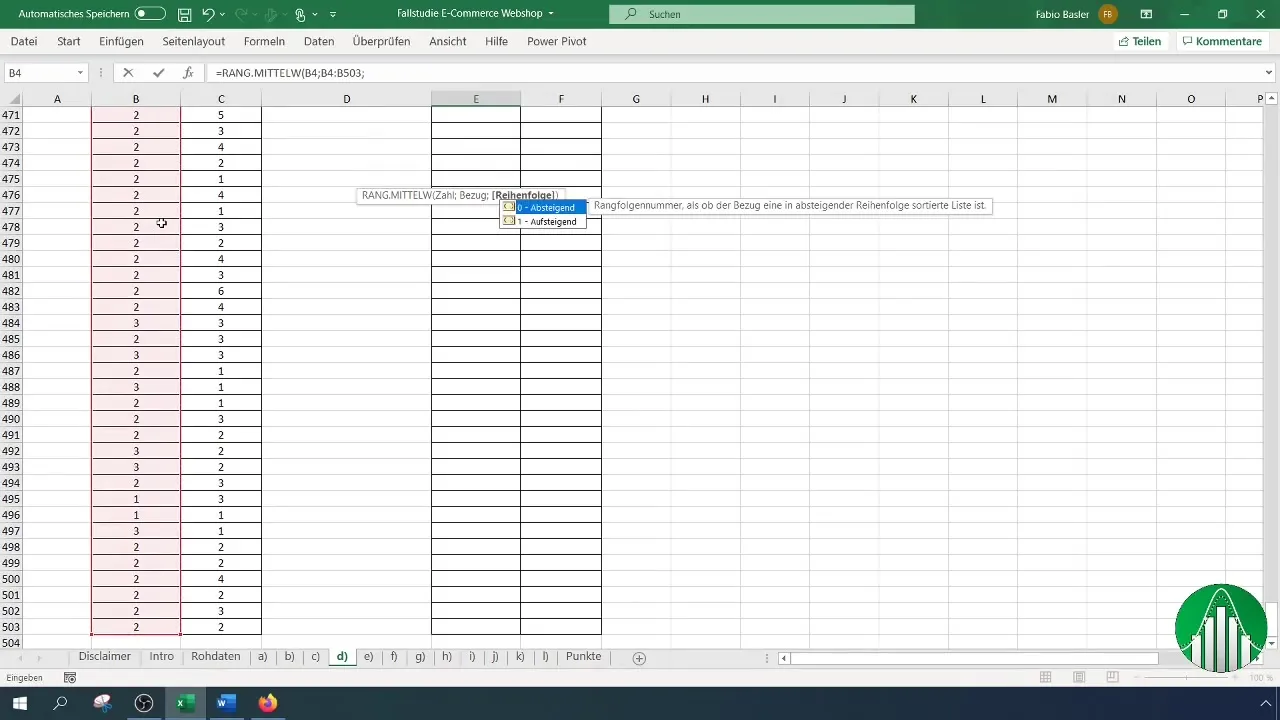
Bedenke bei der Anwendung dieser Formel, dass du die Spalte für die Zufriedenheit markierst und den gesamten Bereich von B4 bis zum Ende deiner Datenreihe festlegst, um die Ränge korrekt zu identifizieren.
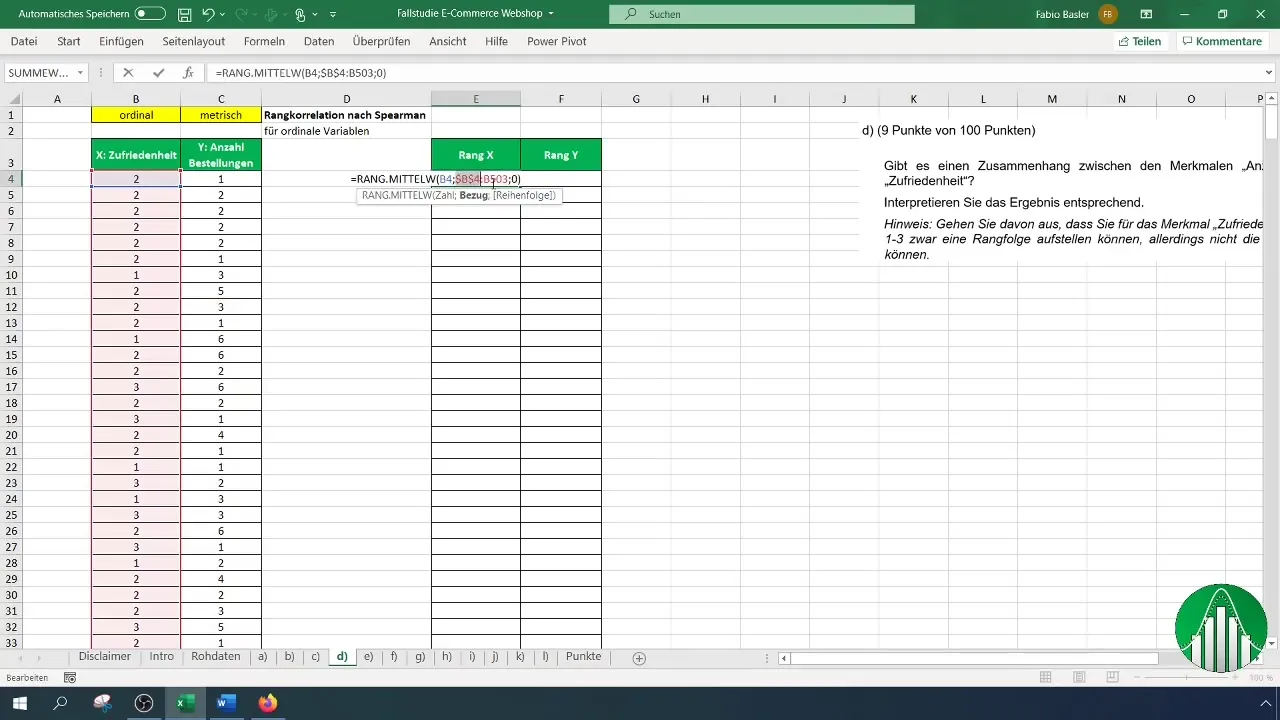
Entscheide dich, ob du die Ränge aufsteigend oder absteigend sortieren möchtest. In der Regel ist es sinnvoll, sie aufsteigend zu sortieren. Betone hierbei, dass die Zellreferenzen für die Ränge fixiert werden, indem du die F4-Taste benutzt. Dies ist wichtig, damit die Referenzen während des Kopierens nicht verändert werden.
Sobald du die Ränge für die Zufriedenheit festgelegt hast, wiederhole den Vorgang für die Anzahl der Bestellungen. Vergewissere dich, dass du die Formel und den Bezug korrekt anwendest.
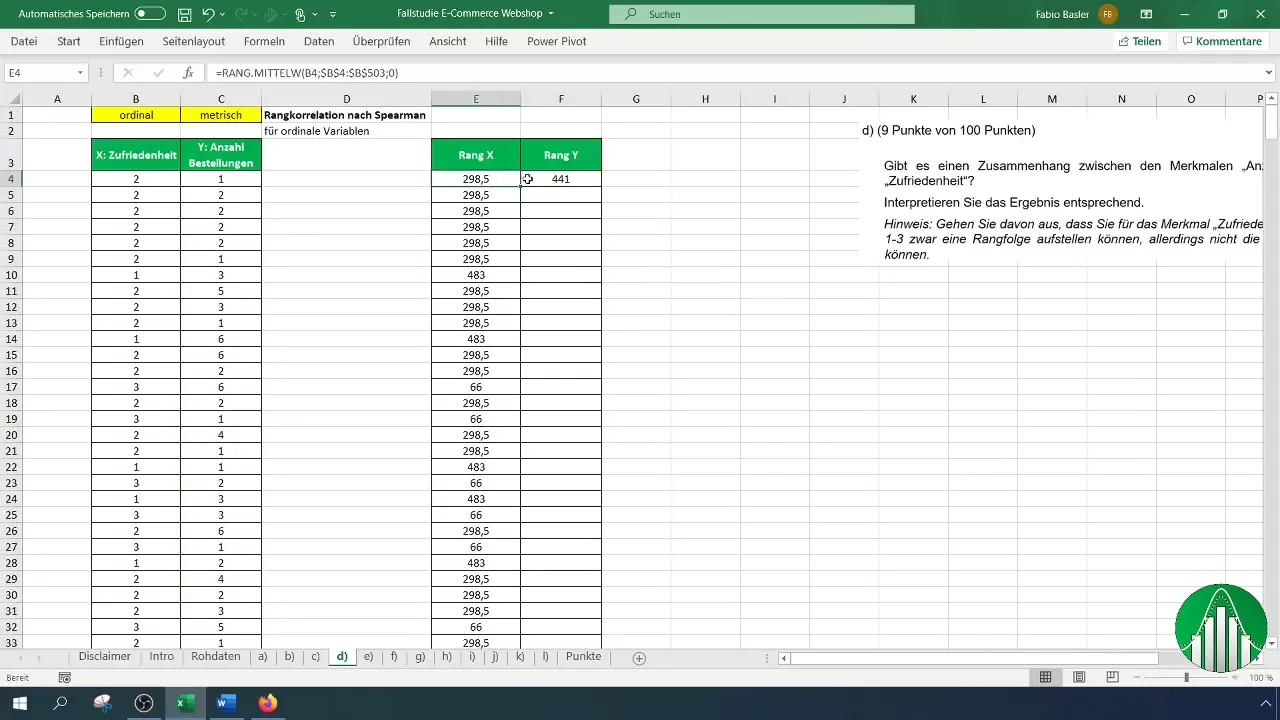
Mit beiden Ranglisten (Zufriedenheit und Anzahl der Bestellungen) bist du bereit, den Rangkorrelationskoeffizienten nach Spearman zu berechnen. Hierzu nutzt du die Formel „=KORREL“, um die Beziehung zu bestimmen. Der Syntax sieht folgendermaßen aus:
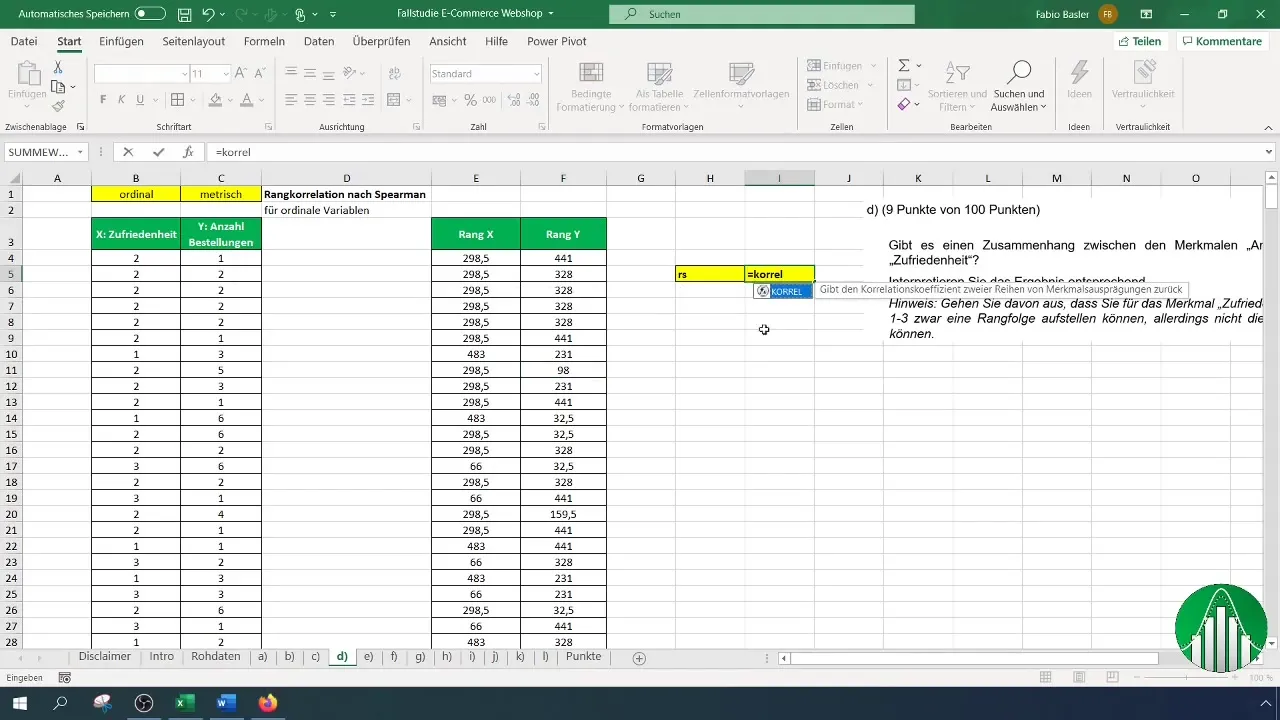
Gib für den ersten Bezug die Rangliste der Zufriedenheit und für den zweiten die Rangliste der Bestellungen an. Excel wird nun automatisch den Spearman’schen Rangkorrelationskoeffizienten berechnen.

Wie lautet das Ergebnis deiner Berechnung? Ein Wert von 5,61% zeigt einen schwachen positiven Zusammenhang zwischen der Zufriedenheit und der Anzahl der Bestellungen an. Dies bedeutet, dass es kaum eine signifikante Beziehung zwischen diesen beiden Variablen gibt.
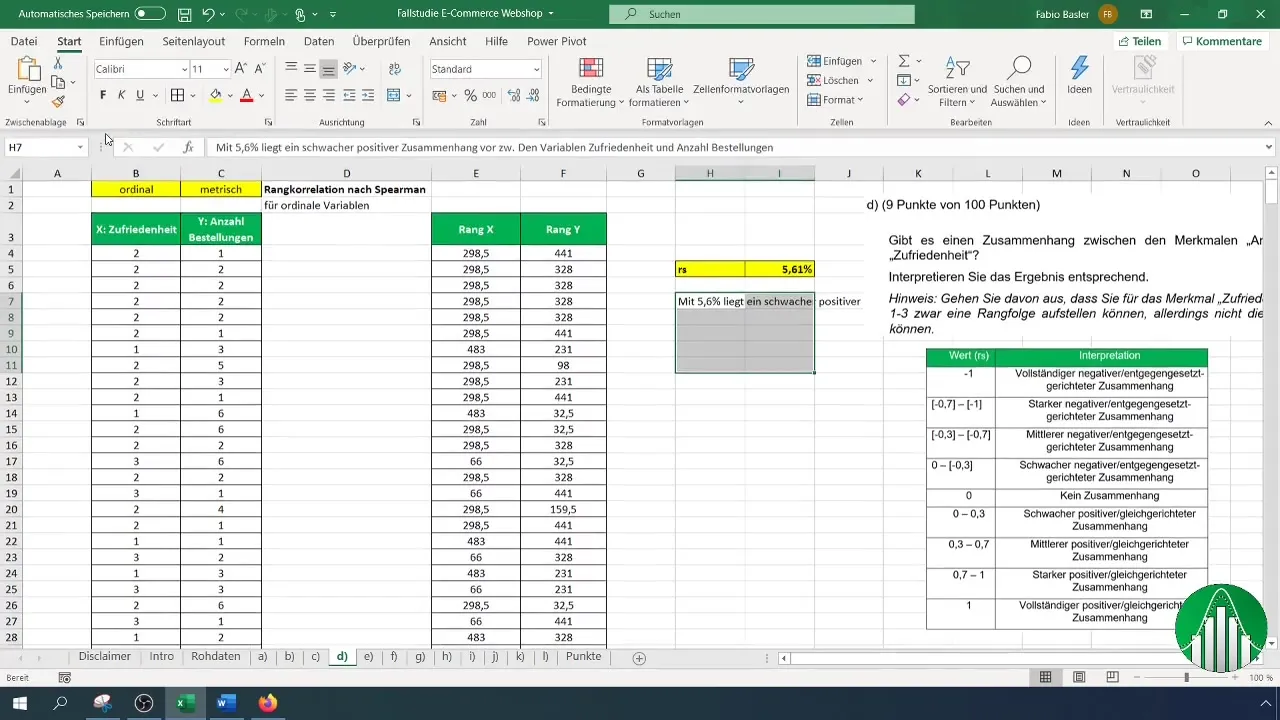
Um deine Ergebnisse zu interpretieren, verwende eine Wertetabelle, in der die verschiedenen Bereiche der Rangkorrelation aufgeführt sind. Nach der Interpretation bestätigen wir, dass die niedrige Korrelationsrate bedeutet, dass die Variablen relativ unabhängig sind.
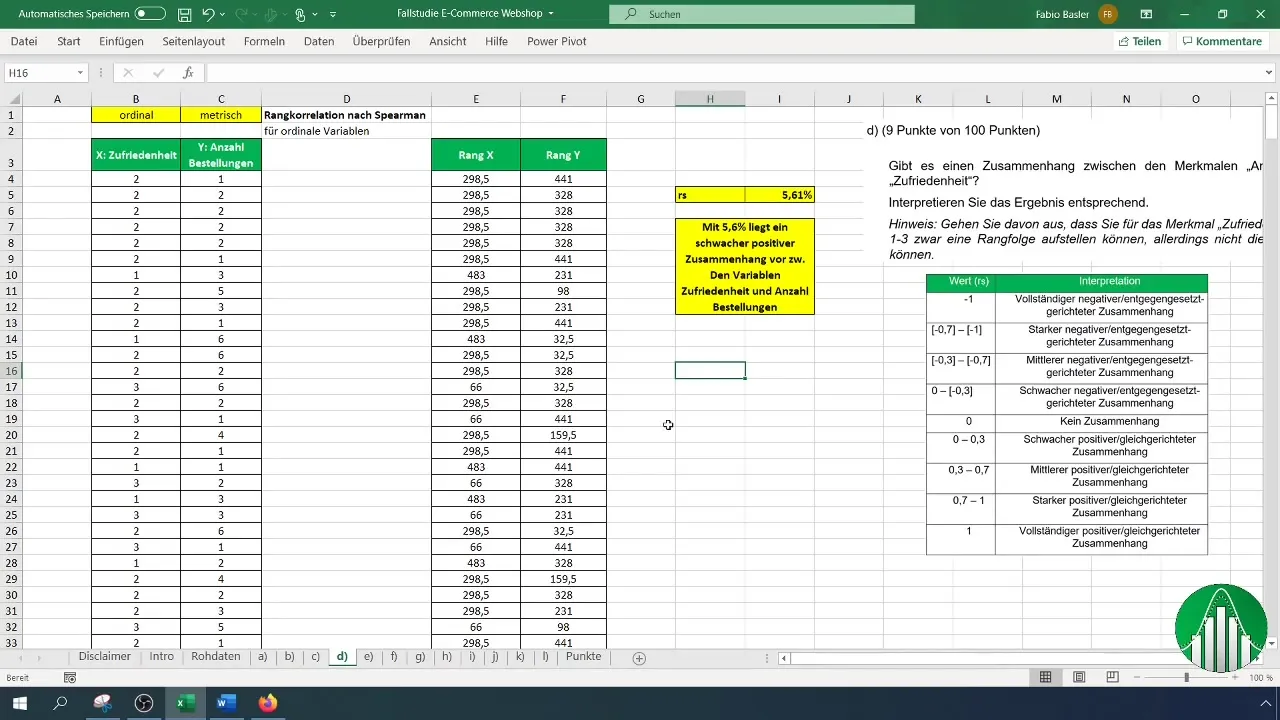
Zusammenfassung
Die Durchführung einer Rangkorrelationsanalyse nach Spearman in Excel ermöglicht es dir, wertvolle Einblicke in die Beziehungen zwischen ordinalen und metrischen Variablen zu gewinnen. Die Methode ist einfach anzuwenden und bietet eine klare Sicht auf etwaige Zusammenhänge.
Häufig gestellte Fragen
Was ist der Spearman-Rangkorrelationskoeffizient?Der Spearman-Rangkorrelationskoeffizient misst die Stärke und Richtung einer monotonen Beziehung zwischen zwei Variablen.
Wann ist die Verwendung des Spearman-Koeffizienten sinnvoll?Er ist sinnvoll, wenn mindestens eine der Variablen ordinal skaliert ist.
Wie berechne ich den Spearman-Koeffizienten in Excel?Verwende die „Rang.Mittel“-Funktion, um die Ränge zu ermitteln, und dann die „KORREL“-Funktion, um den Zusammenhang zu berechnen.
Welcher Wertebereich gilt für den Spearman-Koeffizienten?Der Koeffizient liegt zwischen -1 und 1. Werte nahe 1 deuten auf eine starke positive Korrelation hin, während Werte nahe -1 auf eine starke negative Korrelation hinweisen.
Was kann ein Wert von 5,61% in der Rangkorrelation bedeuten?Ein Wert von 5,61% zeigt einen schwachen positiven Zusammenhang an, was darauf hinweist, dass die Variablen relativ unabhängig sind.


