Normalverteilung in Excel – Wahrscheinlichkeiten einfach berechnen

Die Normalverteilung ist ein zentrales Konzept der Wahrscheinlichkeitstheorie und Statistik. In jeder Datensammlung, die gleichmäßig verteilt ist, beobachten wir die sogenannte Glockenkurve, die oft in Umfragen und Verkaufsanalysen vorkommt. In diesem Tutorial wirst du lernen, wie du mit Excel die Normalverteilung für eine Umfrage berechnen und visualisieren kannst, um entscheidende Wahrscheinlichkeiten zu ermitteln. Mit diesen Fähigkeiten kannst du nicht nur deine Daten besser verstehen, sondern sie auch gezielt nutzen, um fundierte Entscheidungen zu treffen.

Wichtigste Erkenntnisse

• Du lernst die Schritt-für-Schritt-Berechnung der Normalverteilung in Excel.
• Die Möglichkeiten der grafischen Darstellung einer Normalverteilung werden aufgezeigt.
• Du verstehst, wie Wahrscheinlichkeiten für spezifische Ereignisse berechnet werden können.

Schritt-für-Schritt-Anleitung

Zuerst solltest du sicherstellen, dass alle benötigten Daten in einer Excel-Tabelle bereitstehen. Diese Daten repräsentieren beispielsweise die Umsätze aus einer Umfrage.

Visualisierung der Normalverteilung

Um die Normalverteilung des Umsatzes grafisch darzustellen, gehst du wie folgt vor:

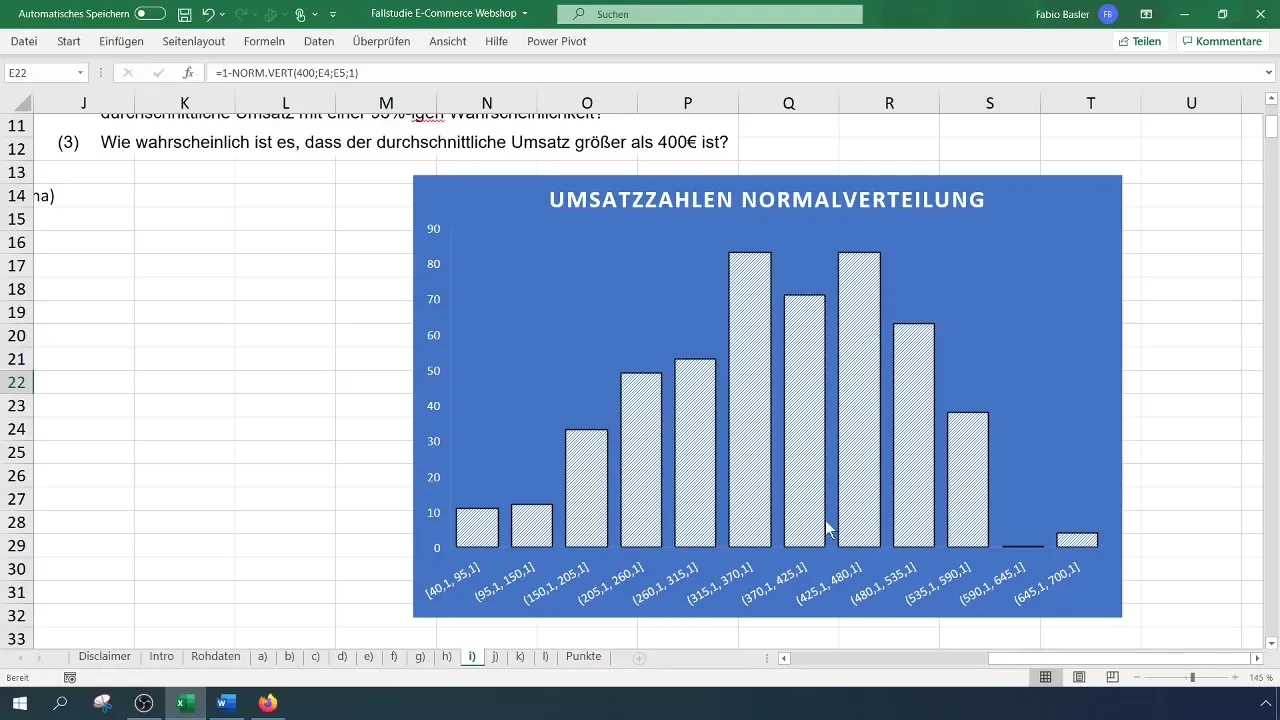
Zunächst wählst du die Umsatzdaten in deiner Excel-Tabelle aus und kopierst sie in eine neue Spalte. In der Menüleiste klickst du auf „Einfügen“ und wählst „Diagramm“. Hier entscheidest du dich für ein Histogramm, um die Verteilung visuell darzustellen. Du kannst ein leeres Histogramm auswählen, um die Standardwerte deiner Daten anzuzeigen.

Klicke mit der rechten Maustaste auf das Diagramm und wähle „Daten auswählen“. In dem sich öffnenden Fenster fügst du deine Umsatzdaten als erste Datenreihe hinzu. In den Reihenwerten wählst du alle Datensätze aus, indem du die Shift-Taste hälst und die Werte auswählst.

Sobald die Daten im Histogramm angezeigt werden, kannst du den Titel des Diagramms anpassen, um es repräsentativer zu machen. Zum Beispiel, ändere den Titel in „Umsatzzahlen Normalverteilung“. Achte darauf, dass die Glockenkurve erkennbar wird; dies deutet auf eine Normalverteilung hin.

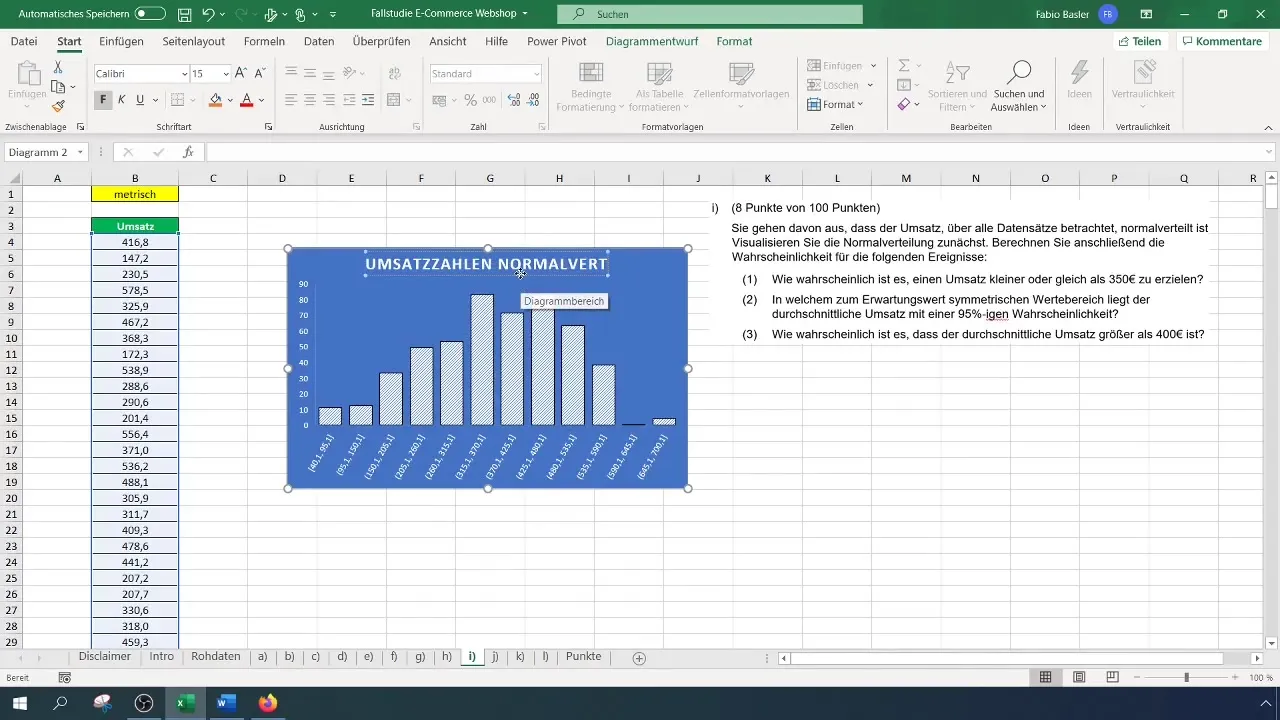
Berechnung von Wahrscheinlichkeiten

Die nächste Aufgabe besteht darin, die Wahrscheinlichkeit zu ermitteln, dass der Umsatz kleiner oder gleich 350 Euro ist. Dafür benötigst du den Mittelwert und die Standardabweichung der Umsatzdaten.

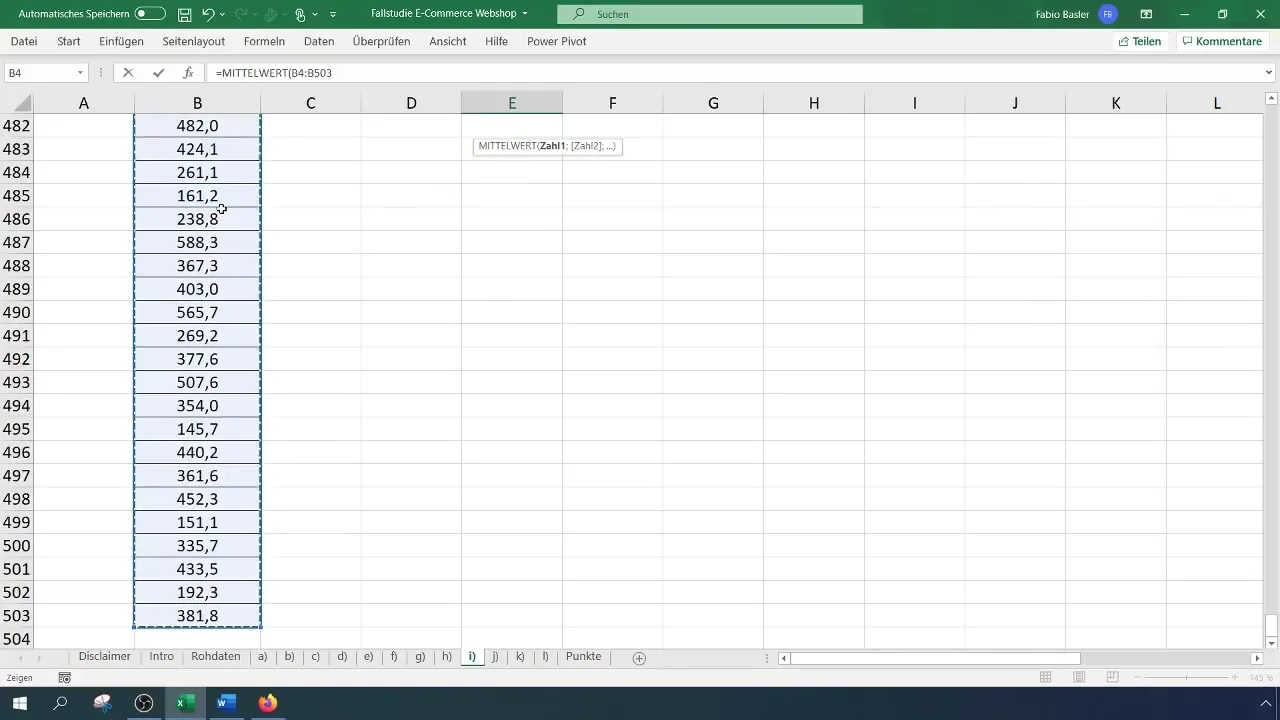
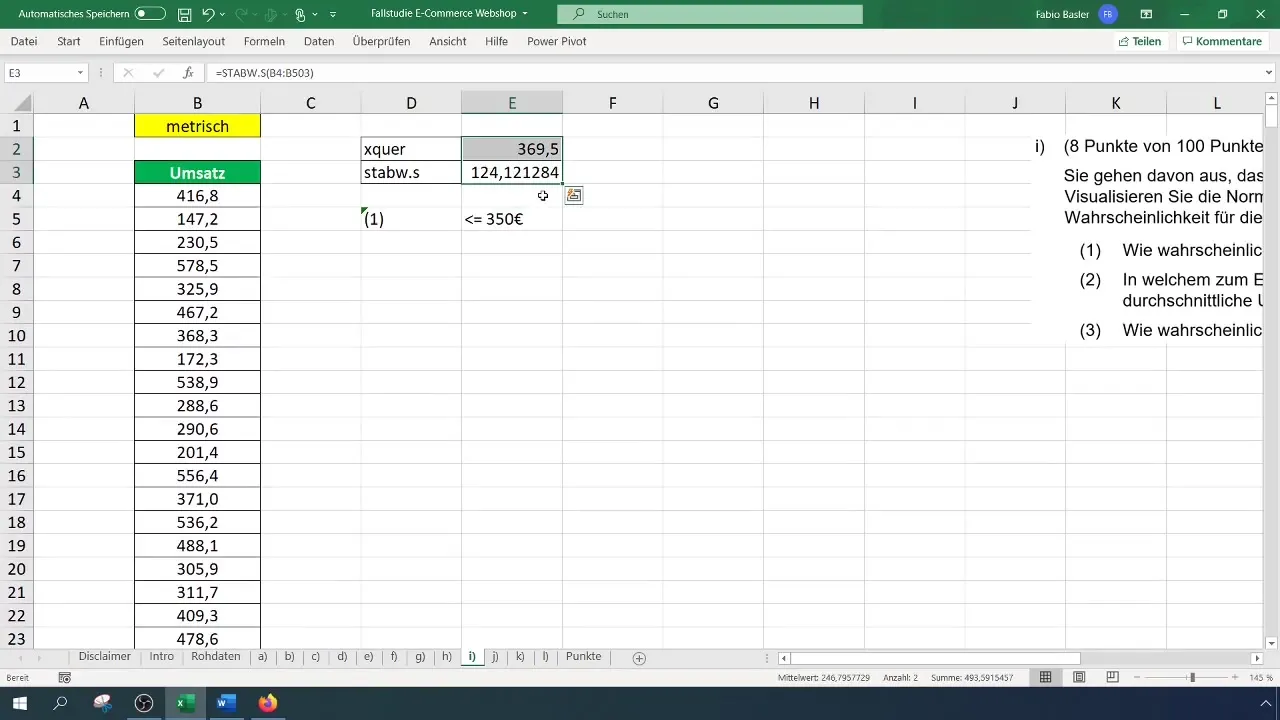
Um den Mittelwert zu berechnen, verwendest du die Formel =MITTELWERT(A1:A100) (Hier ersetzen A1:A100 den tatsächlichen Datenbereich). In deinem Beispiel könnte dies einen durchschnittlichen Umsatz von 369 Euro ergeben.

Für die Standardabweichung nutzt du die Formel =STDEVP(A1:A100), und dies könnte in deinem Fall etwa 124,12 Euro ergeben.

Jetzt kannst du die Wahrscheinlichkeit für einen Umsatz von 350 Euro berechnen. Dies geschieht über die Formel: =NORM.VERT(350; Mittelwert; Standardabweichung; WAHR). Setze die entsprechenden Werte ein und drücke Enter.

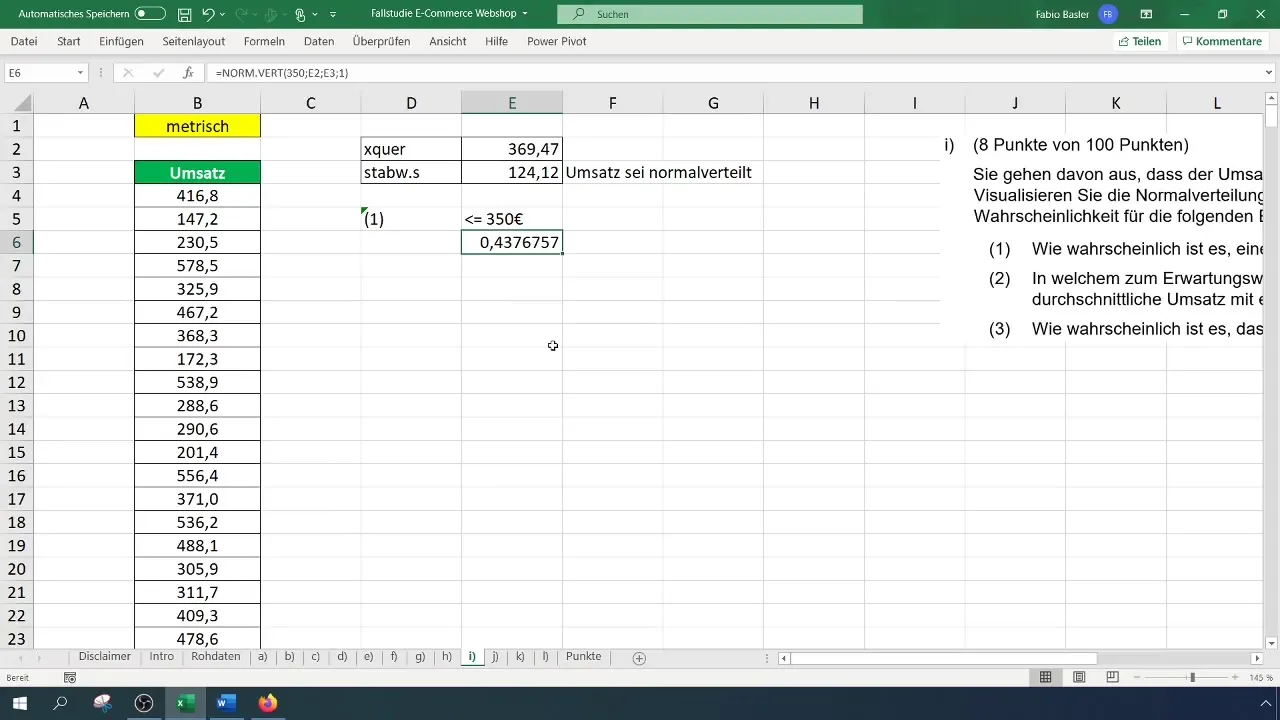
Das Ergebnis dieser Berechnung könnte dir anzeigen, dass die Wahrscheinlichkeit, einen Umsatz kleiner oder gleich 350 Euro zu erzielen, bei ungefähr 43,8 % liegt. Um dies zu veranschaulichen, kannst du die Werte formatieren und auf die Prozentdarstellung umstellen.

Berechnung des symmetrischen Wertebereichs um den Erwartungswert

Das nächste Ziel ist die Bestimmung des symmetrischen Wertebereichs um den Erwartungswert mit einer Wahrscheinlichkeit von 95 %. Hierzu musst du den quantitativen Wert für 95 % bestimmen.

Dies geschieht durch die Eingabe der Formel =NORM.S.INV(0,95) in eine Zelle, was dir den quantilswert von 1,65 liefert.

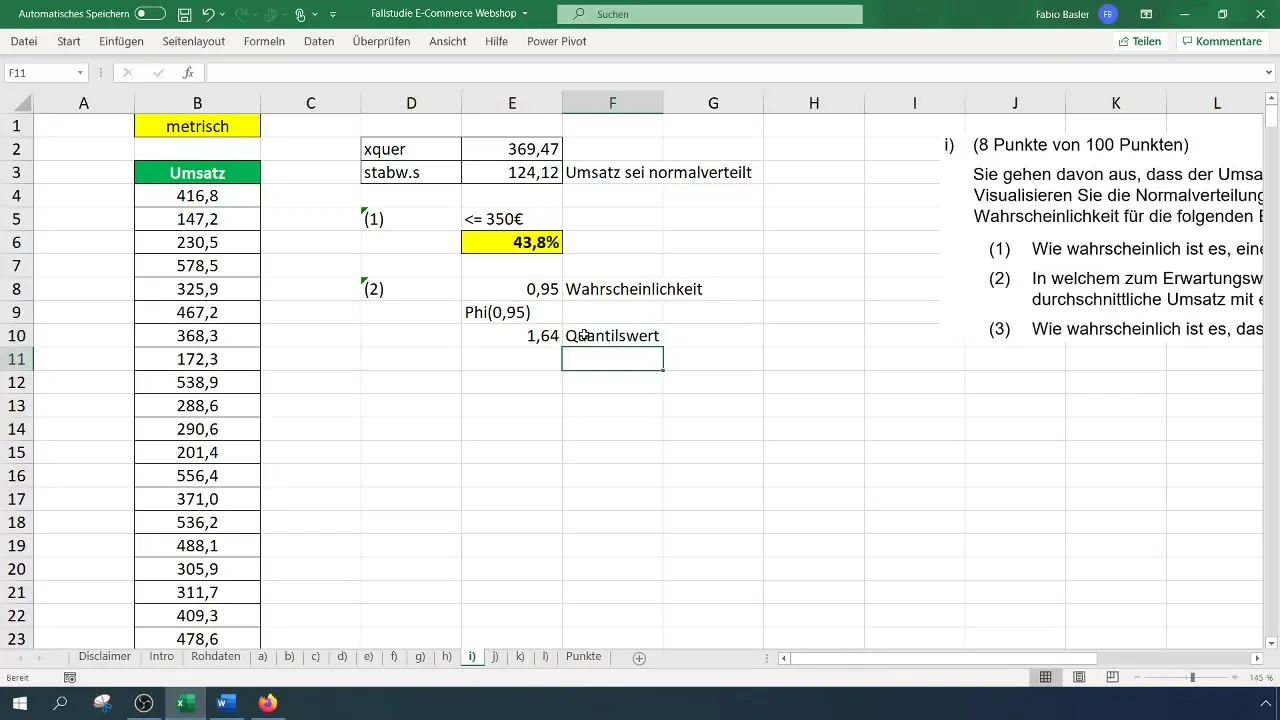
Nun setzt du diese Berechnung in eine Gleichung ein, um den Wertebereich zu finden. Die Formel könnte wie folgt aussehen: Erwartungswert + (Standardabweichung * Quantilswert). Setze die entsprechenden Werte ein und berechne den symmetrischen Wertebereich.

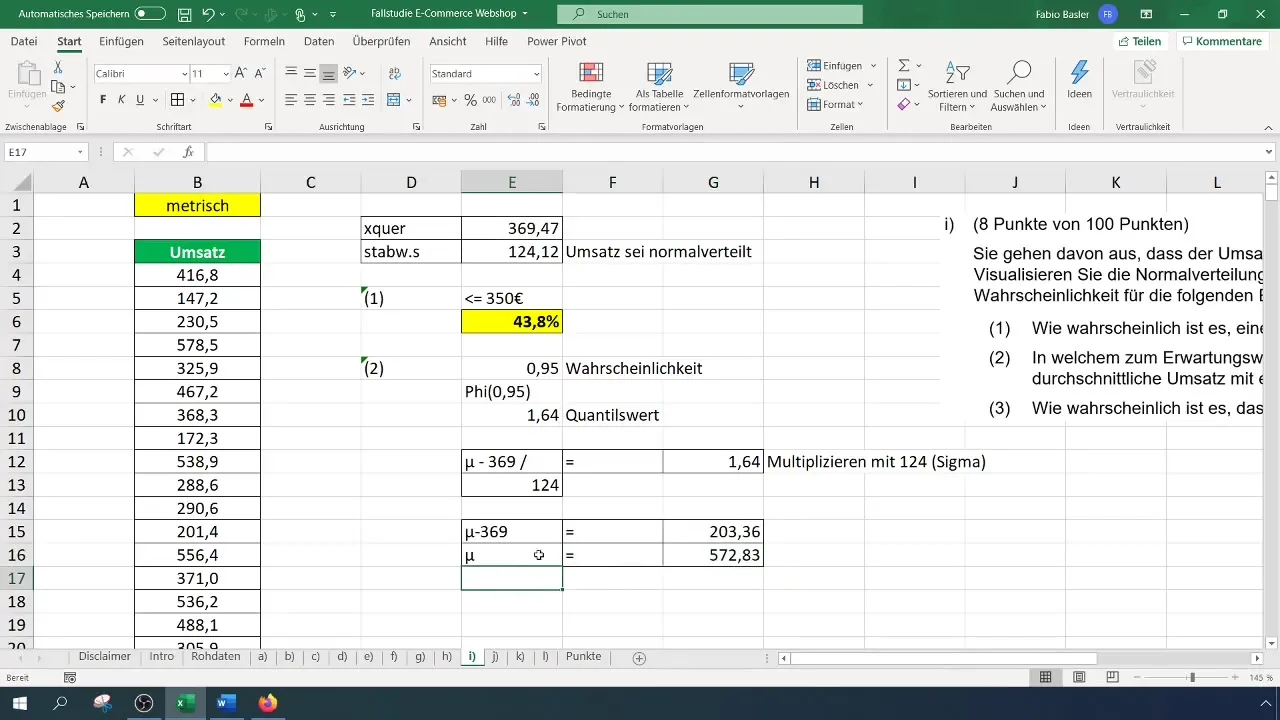
Wenn du beispielsweise einen Wert von 572 Euro erhältst, besagt das, dass du mit einer Wahrscheinlichkeit von 95 % einen Umsatz innerhalb dieses Bereichs erwarten kannst.

Wahrscheinlichkeiten für höhere Umsätze

Für die letzte Berechnung wirst du die Wahrscheinlichkeit bestimmen, dass der Umsatz größer als 400 Euro ist. Hierfür gilt es, die Formel =1 - NORM.VERT(400; Mittelwert; Standardabweichung; WAHR) zu verwenden.

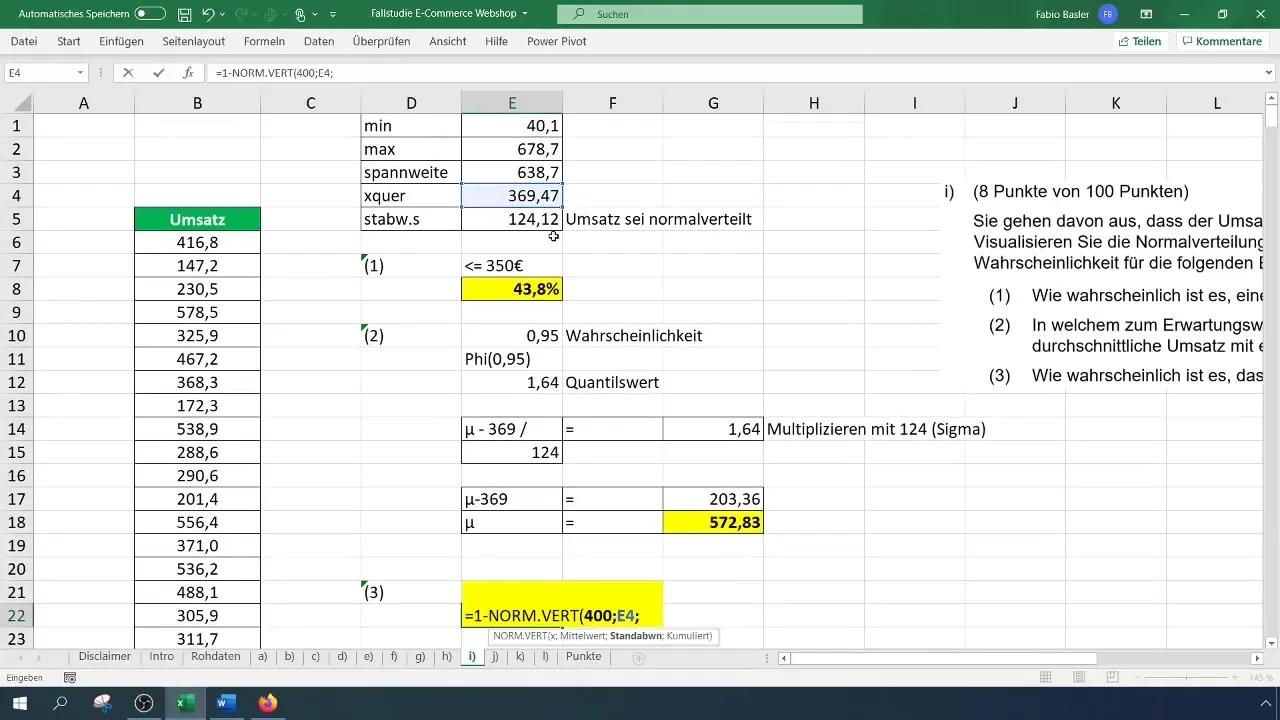
Die Wahrscheinlichkeit könnte sich auch hier um 40 % bewegen. Diese Werte sind sinnvoll zu hinterfragen. Wenn du dir die Skala im Histogramm anschaust, lässt sich die Konsistenz des Prozentsatzes der höheren Umsätze nachvollziehen.

Zusammenfassung

In dieser Anleitung hast du erfahren, wie du mit Excel die Normalverteilung zur Berechnung von Wahrscheinlichkeiten nutzen kannst. Aufgebaut auf praktischen Beispielen aus einer Umfrage, hast du gelernt, wie du sowohl grafisch als auch rechnerisch mit Daten umgehen kannst. Das Verständnis dieser Konzepte wird dir helfen, statistische Analysen in deinen Projekten erfolgreich umzusetzen.