Statistische Berechnungen sind ein unverzichtbarer Bestandteil der Datenanalyse, insbesondere in einem E-Commerce-Umfeld. Die historische Datenanalyse ermöglicht es, Wahrscheinlichkeiten zu ermitteln, die für Unternehmen entscheidend sind. In dieser Anleitung lernst du, wie du Wahrscheinlichkeiten mithilfe der Poissonverteilung in Excel berechnen kannst, basierend auf einem Fallbeispiel einer Umfrage.
Wichtigste Erkenntnisse Die Poissonverteilung ermöglicht es, die Wahrscheinlichkeit von Ereignissen zu bestimmen, die in einem festen Zeitrahmen auftreten. In diesem Beispiel berechnest du die Wahrscheinlichkeit, dass mehr als zwei, aber höchstens vier Kunden in einem E-Commerce-Shop innerhalb einer Stunde etwas kaufen, sowie die Wahrscheinlichkeit, dass mehr als zwei Kunden insgesamt etwas kaufen.
Schritt-für-Schritt-Anleitung
Beginnen wir mit der Berechnung der Wahrscheinlichkeiten für die beschriebenen Ereignisse.
Schritt 1: Grundlagen der Poissonverteilung verstehen
Zuallererst ist es wichtig, dass du verstehst, was die Poissonverteilung ist. Diese diskrete Wahrscheinlichkeitsverteilung dient dazu, die Anzahl von Ereignissen in fixen Zeitperioden zu quantifizieren. Im aktuellen Beispiel haben wir einen Mittelwert von fünf Käufen pro Stunde. Dies formulierst du als Lambda-Wert (λ = 5).

Schritt 2: Daten in Excel vorbereiten
Öffne Excel und bereite eine neue Tabelle vor. Versichere dich, dass du die relevanten Parameter (Lambda und die Anzahl der gewünschten Ereignisse) gut sichtbar hast.
Schritt 3: Wahrscheinlichkeiten für Kundenkäufe ermitteln
Für das erste Szenario möchtest du die Wahrscheinlichkeit berechnen, dass mehr als zwei und höchstens vier Kunden etwas kaufen. Dazu musst du die Wahrscheinlichkeiten für zwei und vier Kunden berechnen und dann deren Differenz ermitteln.

Schritt 4: Excel-Formel für die Poissonverteilung nutzen
Verwende die Funktion POISSON.WAHRSCHEINLICHKEIT, um die Wahrscheinlichkeiten zu berechnen. Die Formel lautet wie folgt:
- Für zwei Käufer: =POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR).
- Für vier Käufer: =POISSON.WAHRSCHEINLICHKEIT(4; 5; WAHR).
Schritt 5: Ergebnisse interpretieren
Nach der Anwendung der Formeln erhältst du two Wahrscheinlichkeiten, beispielsweise 12% für zwei Kunden und 44% für vier Kunden. Nun ziehst du die Wahrscheinlichkeit für zwei Käufer von der für vier Käufer ab, was dir eine Wahrscheinlichkeit von 32% gibt, dass mehr als zwei aber höchstens vier Kunden etwas kaufen.
Schritt 6: Weitere Wahrscheinlichkeiten berechnen
Jetzt geht es darum, die Wahrscheinlichkeit zu berechnen, dass mehr als zwei Kunden in deinem E-Commerce-Shop kaufen. Dazu berechnest du zunächst die Wahrscheinlichkeit für genau zwei Käufer und ziehst dieses Ergebnis von 1 ab.
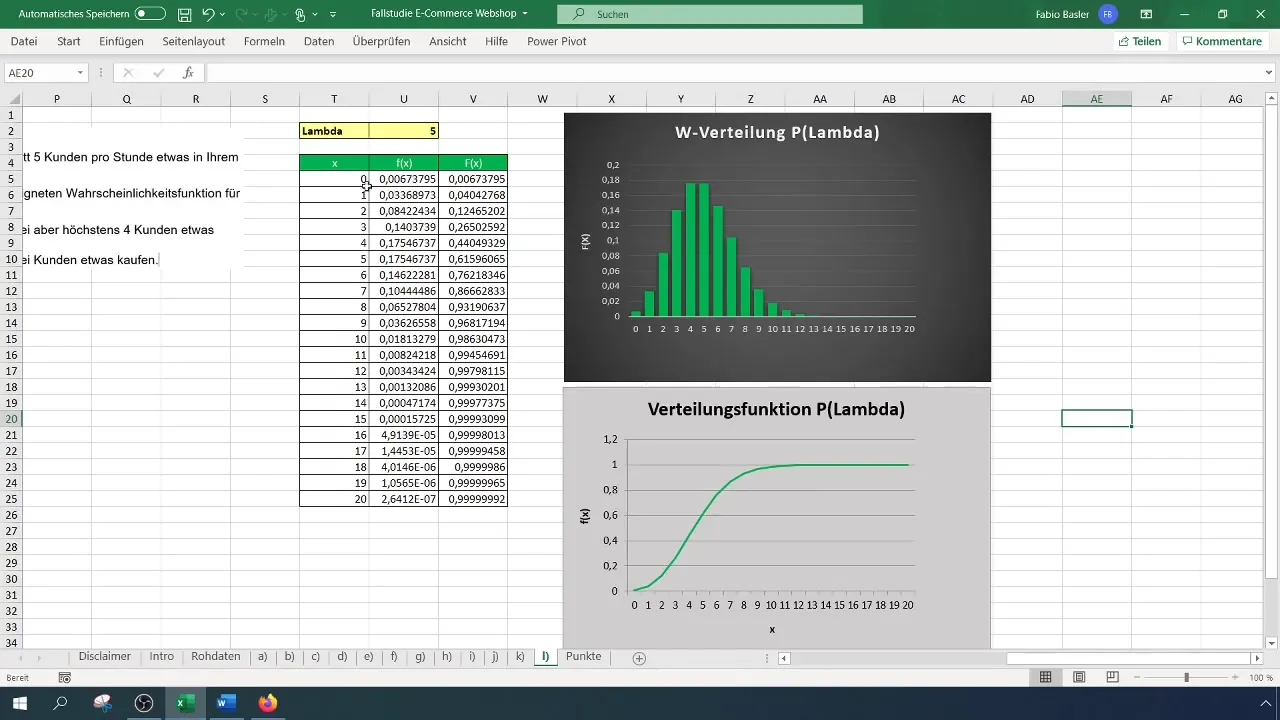
Schritt 7: Excel-Formel für mehr als zwei Käufer verwenden
Die Excel-Formel lautet: =1 - POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR). Dies gibt dir die Wahrscheinlichkeit, dass mehr als zwei Kunden etwas kaufen, die in diesem Fall 88% beträgt.
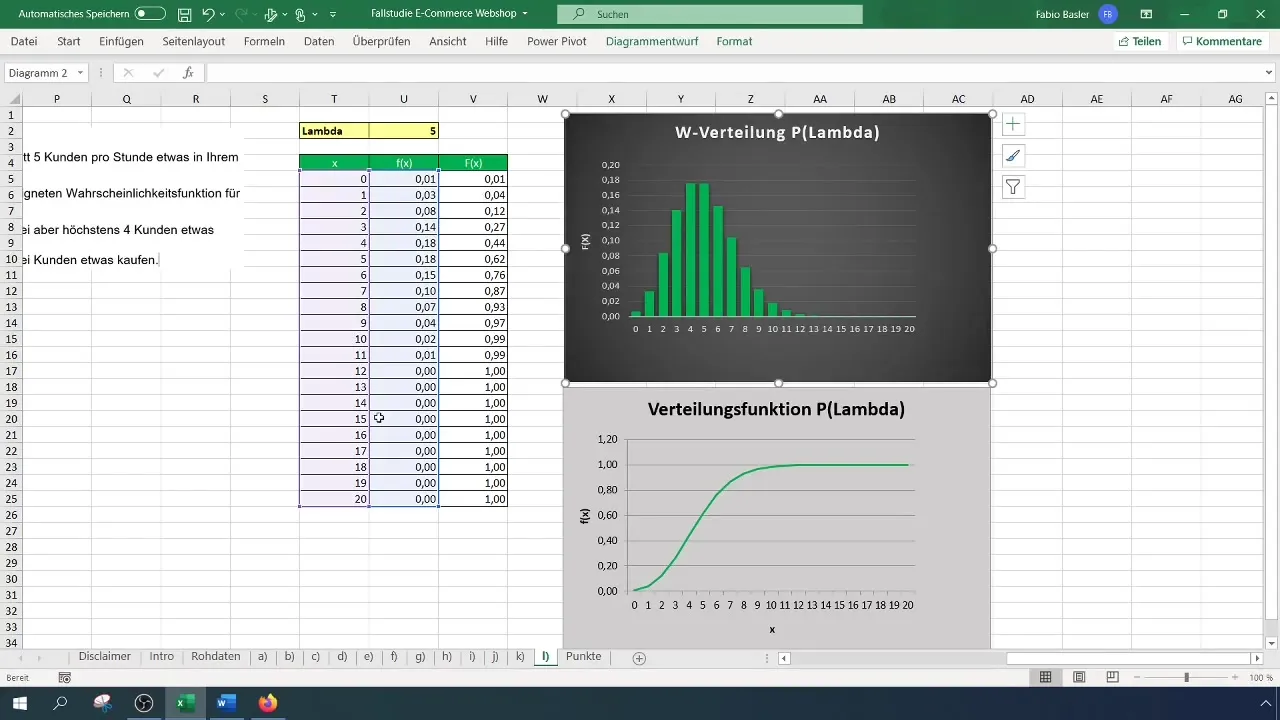
Schritt 8: Zusammenfassung der Ergebnisse
Nachdem du alle Berechnungen durchgeführt hast, notierst du die wesentlichen Wahrscheinlichkeiten. Du hast herausgefunden, dass die Wahrscheinlichkeit, dass mehr als zwei, aber höchstens vier Kunden bestellen, 32% beträgt, während die Wahrscheinlichkeit, dass mehr als zwei Kunden insgesamt etwas kaufen, 88% beträgt.
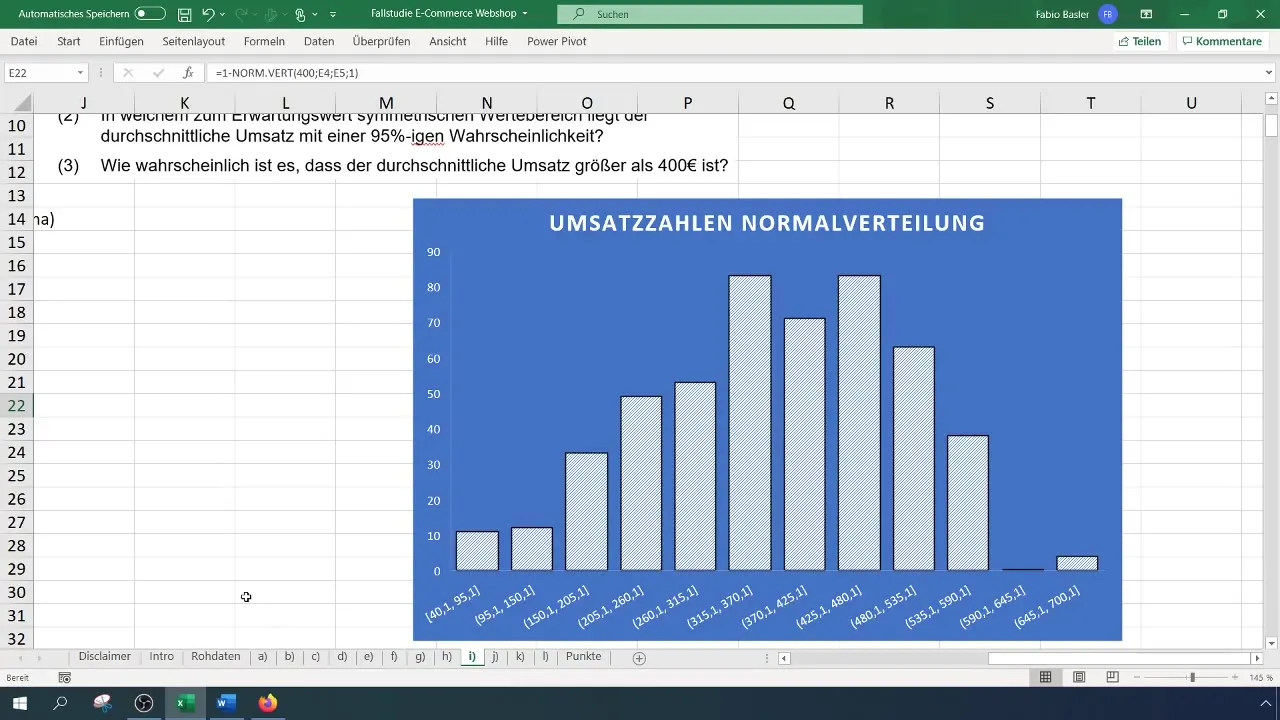
Zusammenfassung
In dieser Anleitung hast du gelernt, wie du die Poissonverteilung zur Berechnung von Wahrscheinlichkeiten in Excel nutzen kannst. Du hast Schritte durchgeführt, um Wahrscheinlichkeiten für spezifische Ereignisse zu berechnen und interpretieren.
Häufig gestellte Fragen
Was ist die Poissonverteilung?Die Poissonverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die angibt, wie viele Male ein Ereignis in einem festen Zeitraum auftritt.
Wie berechne ich Wahrscheinlichkeiten mit der Poissonverteilung in Excel?Du verwendest die Funktion POISSON.WAHRSCHEINLICHKEIT, um Wahrscheinlichkeiten für unterschiedliche Werte zu berechnen.
Was bedeutet ein Lambda-Wert von 5?Ein Lambda-Wert von 5 bedeutet, dass im Durchschnitt fünf Ereignisse (z.B. Käufe) in der definierten Zeitspanne (z.B. einer Stunde) auftreten.
Welche Werte muss ich für die Poissonverteilung angeben?Du musst die Anzahl der gewünschten Ereignisse (x), den Mittelwert (λ) und angeben, ob du kumulierte Wahrscheinlichkeiten berechnen möchtest.
Warum ist die Poissonverteilung wichtig für E-Commerce?Die Poissonverteilung hilft, Kaufmuster zu analysieren und die Wahrscheinlichkeit von Kundenaktivitäten vorherzusagen, was wichtige Entscheidungen im Marketing und Bestandsmanagement unterstützen kann.


