Αντιμετωπίζετε την πρόκληση του αποτελεσματικού προσδιορισμού των τάσεων σε χρονοσειρές; Τότε η εκθετική εξομάλυνση είναι μια μέθοδος που μπορεί να σας βοηθήσει να κάνετε πιο ακριβείς προβλέψεις. Σε αυτό το σεμινάριο, θα μάθετε βήμα προς βήμα πώς να εκτελείτε εκθετική εξομάλυνση στο Excel για να αναλύετε και να απεικονίζετε τις τάσεις στα δεδομένα. Μαζί θα δούμε πώς μπορείτε να επιτύχετε ουσιαστικά αποτελέσματα με ελάχιστη προσπάθεια.
Βασικά ευρήματα
- Η εκθετική εξομάλυνση επιτρέπει μια πιο λεπτή προσαρμογή στις τάσεις των χρονοσειρών.
- Χρήση παραμέτρου εξομάλυνσης (άλφα) 0,15 για τον υπολογισμό τάσεων.
- Υπολογισμός συνιστωσών διακύμανσης και εποχικών τιμών για καλύτερη ανάλυση.
Οδηγίες βήμα προς βήμα
Βήμα 1: Προετοιμασία των δεδομένων
Πρώτα απ' όλα, χρειάζεστε έναν πίνακα με τα σχετικά δεδομένα που θέλετε να αναλύσετε. Θα πρέπει να εισαγάγετε τα δεδομένα στο Excel, με τις ημερομηνίες και τις αντίστοιχες ποσότητες σε διπλανές στήλες. Αντιγράψτε όλες τις απαιτούμενες τιμές, ιδίως τις μεταφερόμενες ημερομηνίες και ποσότητες. Αυτές οι τιμές αποτελούν τη βάση για την ανάλυσή σας.
Βήμα 2: Καθορισμός παραμέτρων εξομάλυνσης
Πριν ξεκινήσετε με την εκθετική εξομάλυνση, πρέπει να ορίσετε την παράμετρο εξομάλυνσης. Πρόκειται συνήθως για μια τιμή μεταξύ 0 και 1 που καθορίζει πόσο έντονα σταθμίζονται οι τελευταίες παρατηρήσεις. Στην προκειμένη περίπτωση, έχουμε επιλέξει μια τιμή άλφα 0,15. Αυτή η τιμή είναι δημοφιλής και αποτελεσματική στην ανάλυση χρονοσειρών, καθώς δεν εστιάζει υπερβολικά στις πιο πρόσφατες τιμές ούτε είναι υπερβολικά συντηρητική.
Βήμα 3: Εκτέλεση υπολογισμού τάσης
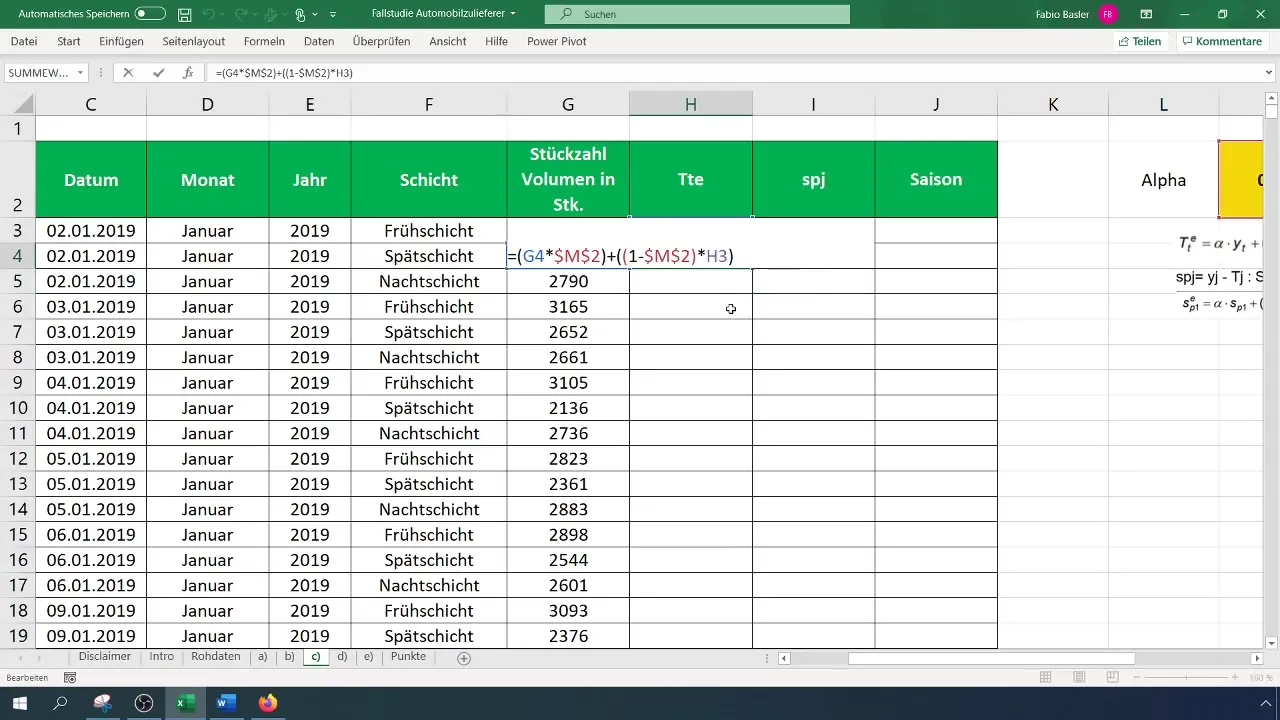
Το επόμενο στοιχείο είναι ο υπολογισμός της τάσης. Για να το κάνετε αυτό, ξεκινήστε εισάγοντας τον τύπο για την εκθετική εξομάλυνση στο αντίστοιχο κελί. Βεβαιωθείτε ότι αφήνετε το πρώτο σημείο παρατήρησης αμετάβλητο. Από το δεύτερο σημείο και μετά, ο τύπος εφαρμόζεται σταθμίζοντας τον τελευταίο υπολογισμένο αριθμό τάσης με την τιμή άλφα. Το περιεχόμενο του κελιού σας θα μπορούσε να μοιάζει ως εξής
[ T_t = \alpha \cdot Yt + (1 - \alpha) \cdot T{t-1} ]
Χρησιμοποιήστε αυτόν τον τύπο για να υπολογίσετε την πρώτη τιμή τάσης και στη συνέχεια σύρετε τον τύπο προς τα κάτω για να βρείτε τις επόμενες τιμές τάσης.
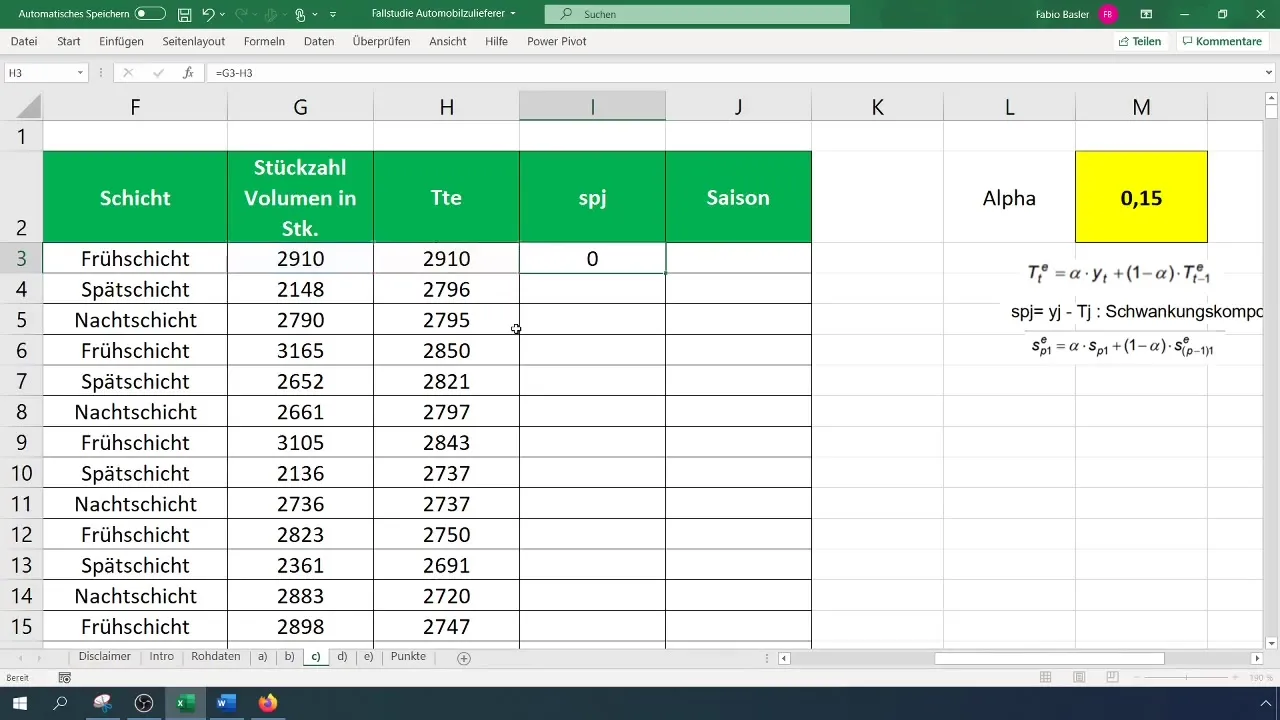
Βήμα 4: Υπολογισμός της συνιστώσας διακύμανσης
Μετά τον υπολογισμό της τάσης, ήρθε η ώρα να προσδιοριστεί η συνιστώσα διακύμανσης. Αυτό γίνεται απλά λαμβάνοντας τη διαφορά μεταξύ των πραγματικών τιμών και των τιμών τάσης. Ο τύπος γι' αυτό είναι
[ S_j = Y_j - T_j ]
Μην ξεχάσετε να εκτελέσετε αυτόν τον υπολογισμό για κάθε σημείο δεδομένων που αναλύετε.
Βήμα 5: Προσδιορισμός των εποχικών τιμών
Το επόμενο βήμα περιλαμβάνει τον προσδιορισμό των εποχικών τιμών. Πρώτον, πρέπει να προσδιορίσετε τον αριθμό των υποπεριόδων στα δεδομένα σας. Εδώ θα συνειδητοποιήσετε ότι θα πρέπει γενικά να έχετε μια ορισμένη κανονικότητα στα δεδομένα. Σημειώστε τον αριθμό των υποπεριόδων, καθώς αυτός είναι απαραίτητος για τους εποχικούς υπολογισμούς.
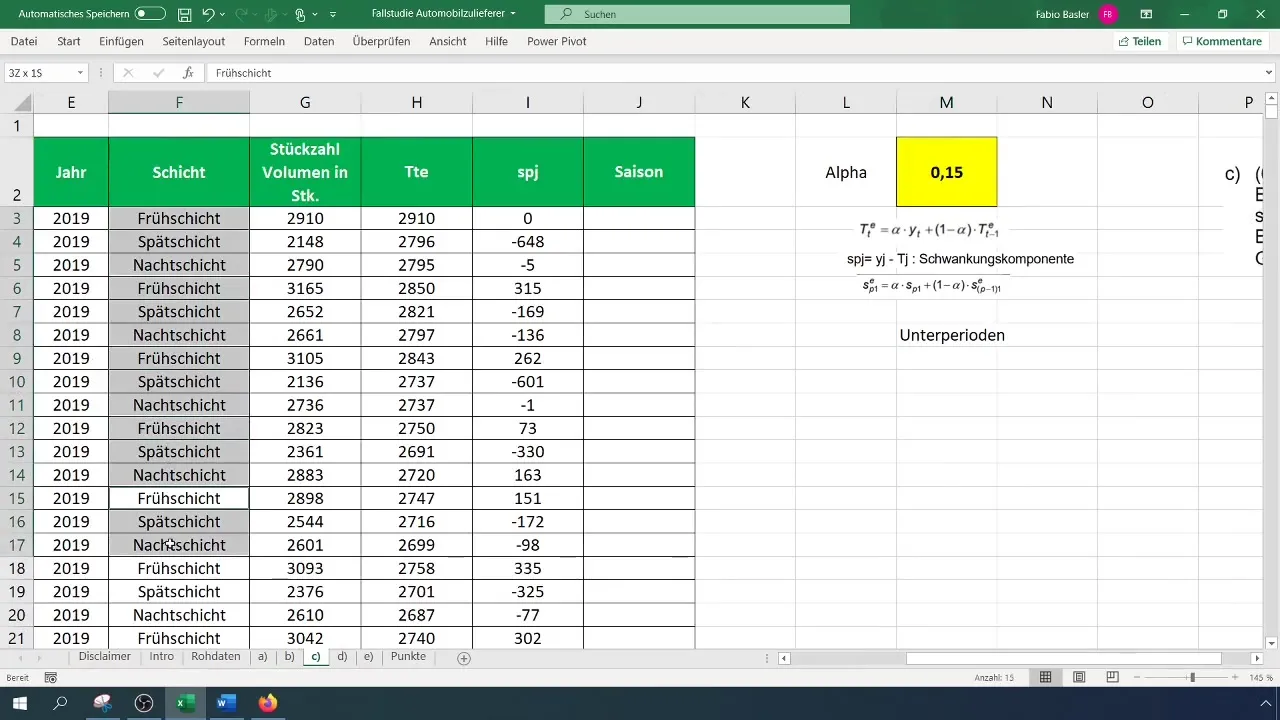
Τώρα που χρειάζεστε τις εποχικές τιμές, ξεκινήστε με τις πρώτες παρατηρήσεις και κάντε τους υπολογισμούς για τις εποχικές τιμές από το τέταρτο σημείο και μετά πολλαπλασιάζοντας τις προηγούμενες διακυμάνσεις με το άλφα και μια αντίθετη τιμή άλφα (1 - άλφα). Φροντίστε να διορθώσετε τους τύπους ανάλογα πριν από την αντιγραφή, ώστε να έχετε τα αποτελέσματα για τα επόμενα σημεία.
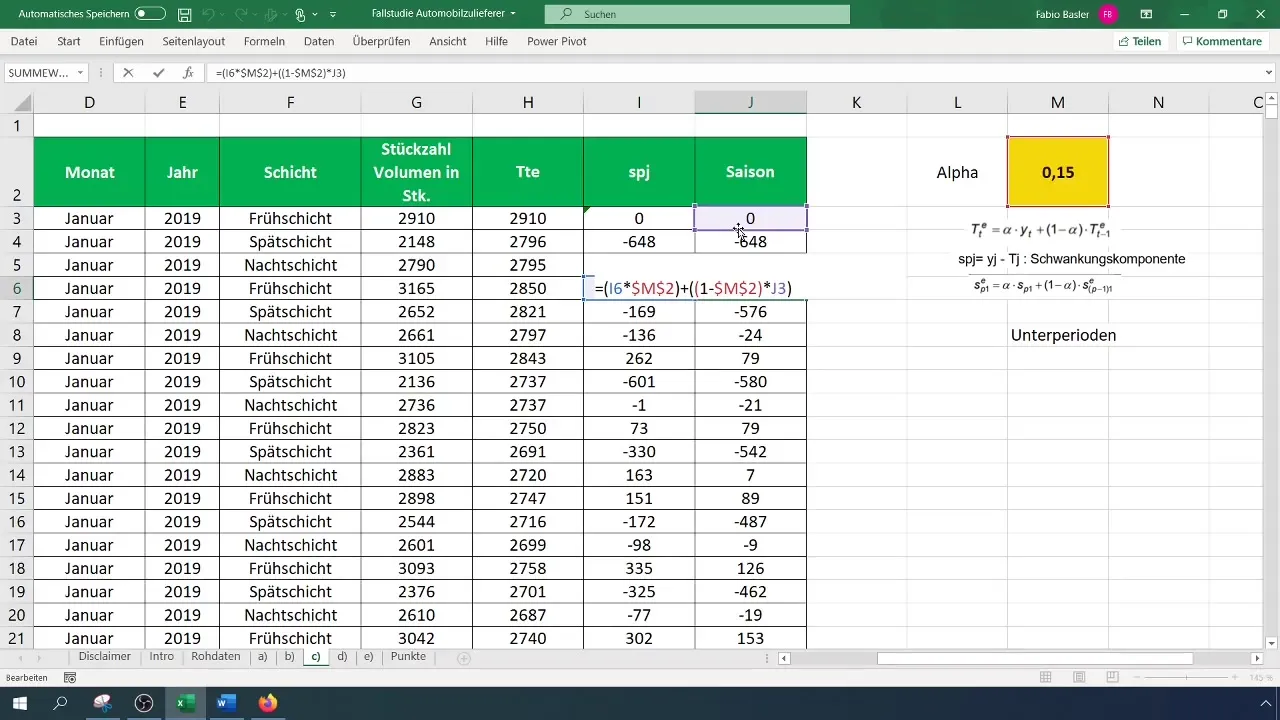
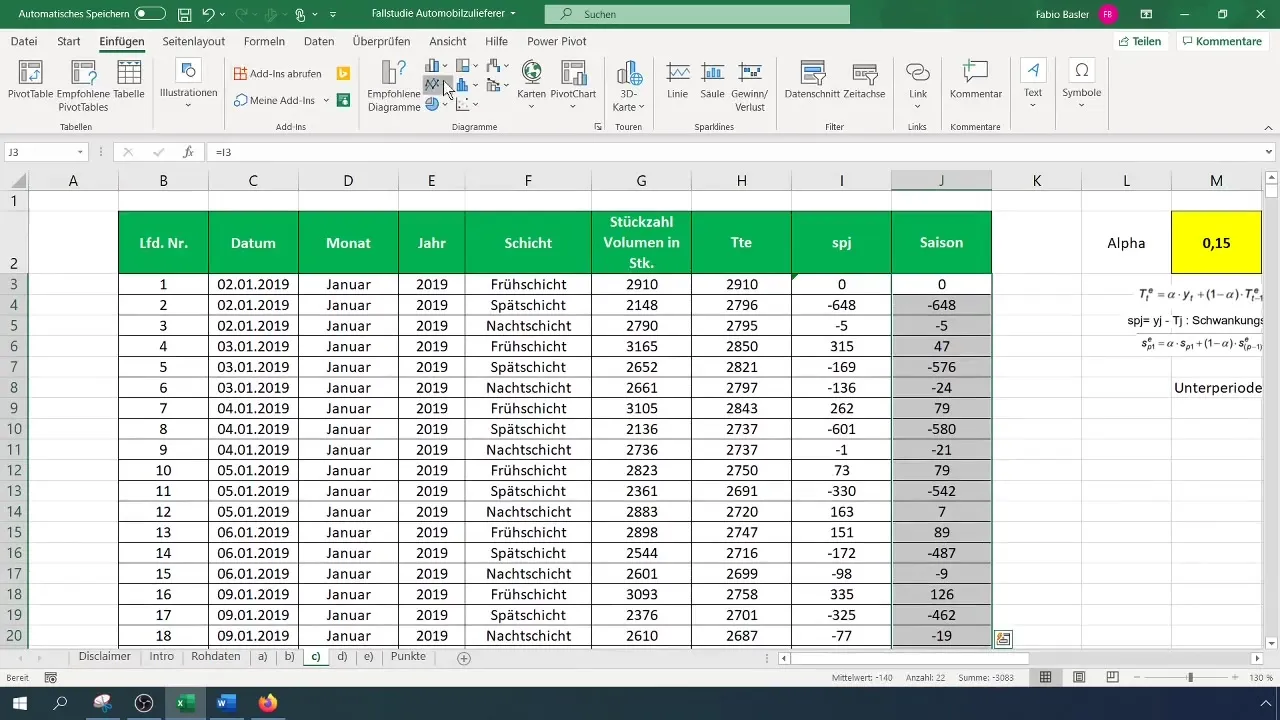
Βήμα 6: Οπτικοποίηση των αποτελεσμάτων
Μια γραφική αναπαράσταση είναι χρήσιμη για την καλύτερη κατανόηση των ευρημάτων σας. Οπτικοποιήστε τις εποχικές τιμές σε ένα γραμμικό διάγραμμα για να δείτε τις τάσεις και τα πιθανά κυκλικά μοτίβα. Μπορείτε να βελτιώσετε την ορατότητα των δεδομένων σας τονίζοντας τις τιμές για τον πρώτο μήνα.
Συνοπτική παρουσίαση
Έχετε πλέον μάθει τα βασικά στοιχεία για την εκτέλεση εκθετικής εξομάλυνσης στο Excel. Από την εισαγωγή δεδομένων έως τον υπολογισμό τάσεων και διακυμάνσεων και την εποχιακή ανάλυση, έχετε αποκτήσει ένα αποτελεσματικό εργαλείο για την απόκτηση πολύτιμων πληροφοριών σχετικά με τα δεδομένα χρονοσειρών.


