Calculation of the two-sided confidence interval in Excel

It is crucial to make informed decisions in the business and sales environment based on data analysis. A two-sided confidence interval allows you to determine the range in which the true average value of a parameter can be found with a certain probability. In this guide, I will show you how to calculate the range of the interval limits for the weekly sales of a sales team using Excel with a confidence probability of 93%.

Main Insights

Key aspects of the two-sided confidence interval include:

1. Calculating the mean as an estimate for the parameter.
2. Determining the standard deviation from the sample.
3. Applying the formulas to determine the lower and upper limits of the interval.
4. Taking into account the confidence probability to position the interval.

Step-by-Step Guide

First, you need a solid understanding of the terms and steps outlining this process.

Step 1: Data Preparation

First, you should prepare the data for Sales Team A. Filter the relevant data accordingly and copy it into your Excel document.

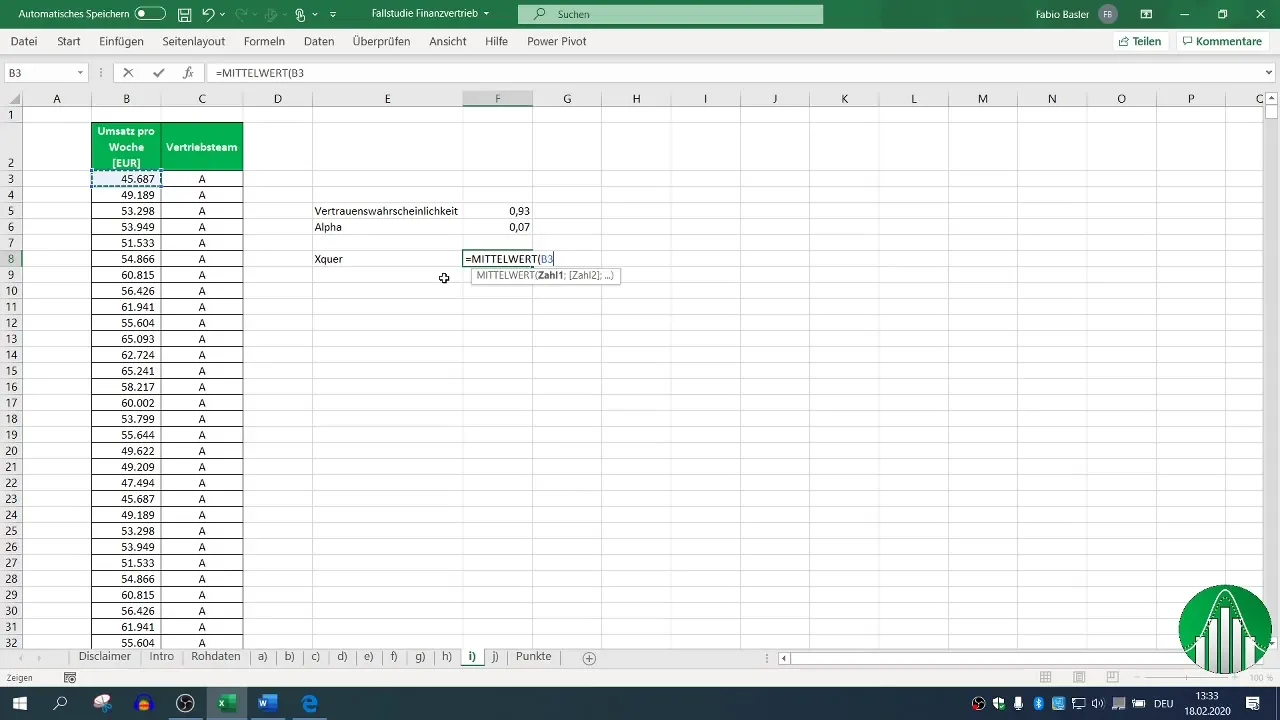
Step 2: Calculating the Mean

To calculate the confidence interval, the first step is determining the mean, which serves as an estimate for the expected revenue. In Excel, you can do this using the formula =AVERAGE(Range), where "Range" is the cell(s) containing the data for Sales Team A's weekly revenue.

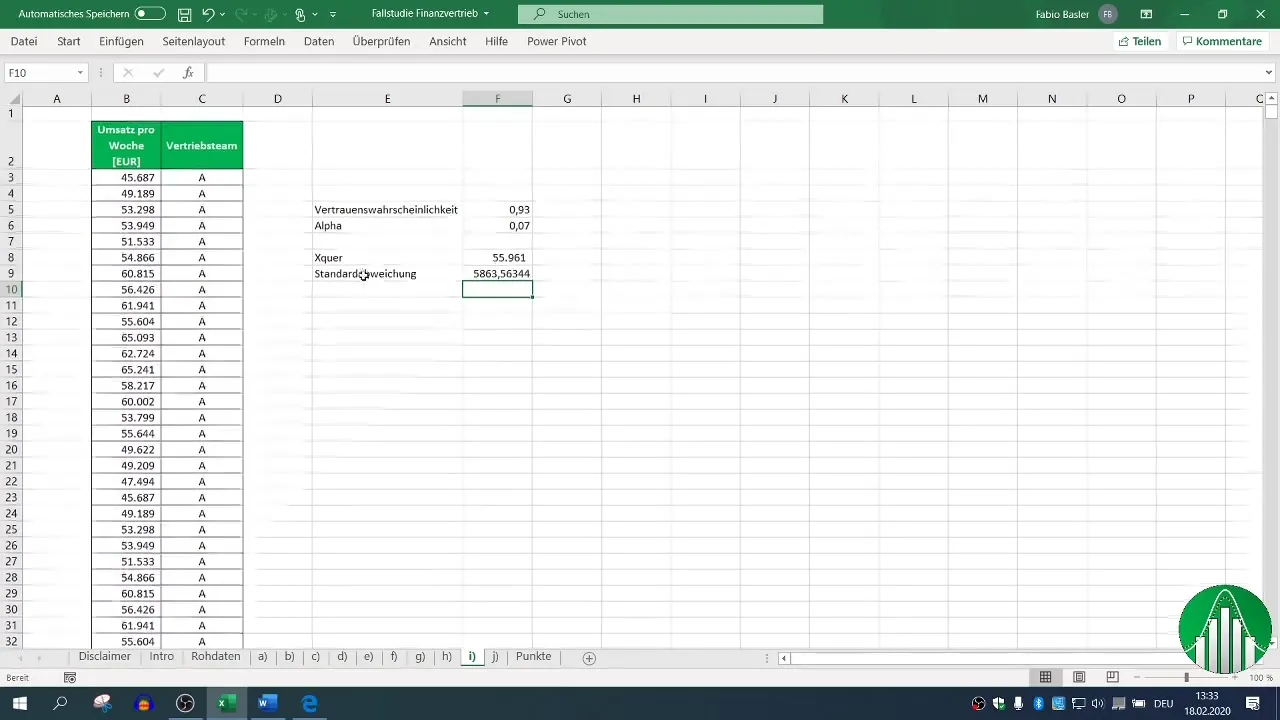
Step 3: Calculating the Standard Deviation

The standard deviation (σ) is important for calculating the two-sided confidence interval. You can calculate it in Excel using the formula =STDEV.S(Range). Ensure you choose the appropriate formula for the sample standard deviation.

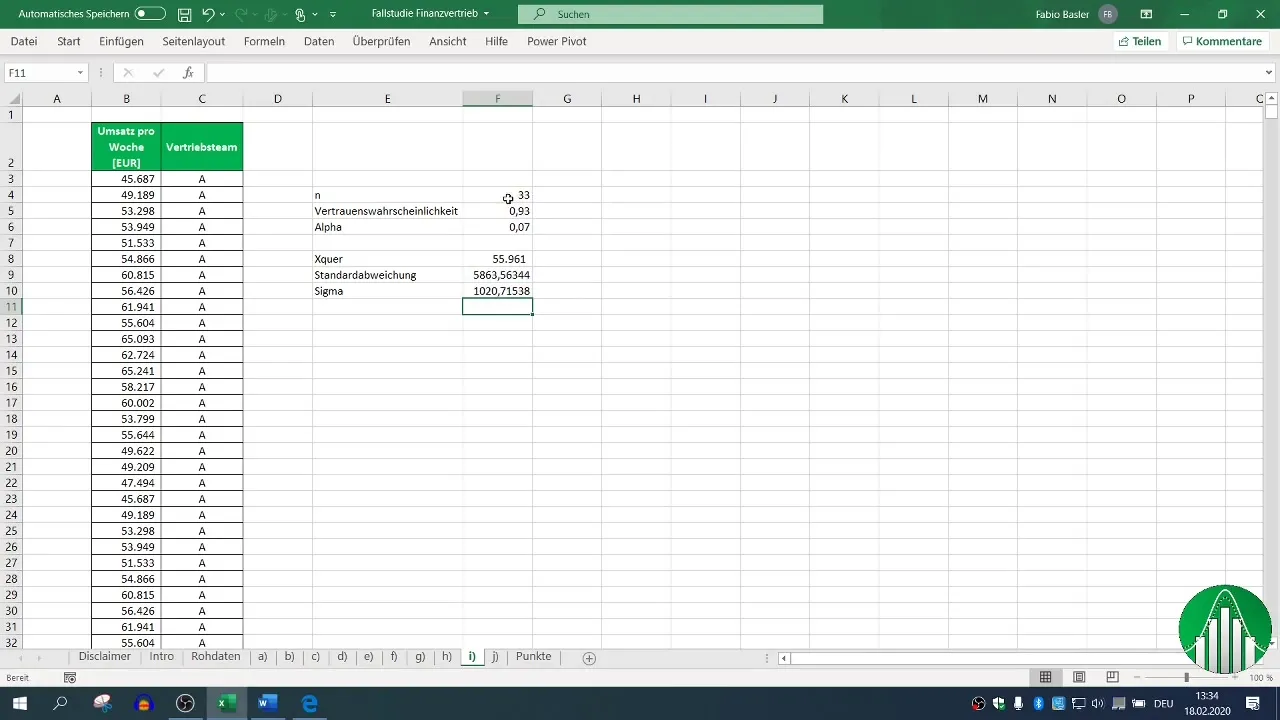
Step 4: Determining the Sample Size

Next, you need to determine the sample size (n). Sum up the number of records you have collected for Sales Team A. In this example, we assume 33 records.

Step 5: Calculating the Standard Deviation of the Mean (σ_m)

For calculating the confidence interval, it is necessary to calculate the standard deviation of the mean, which is simply the standard deviation divided by the square root of the sample size.

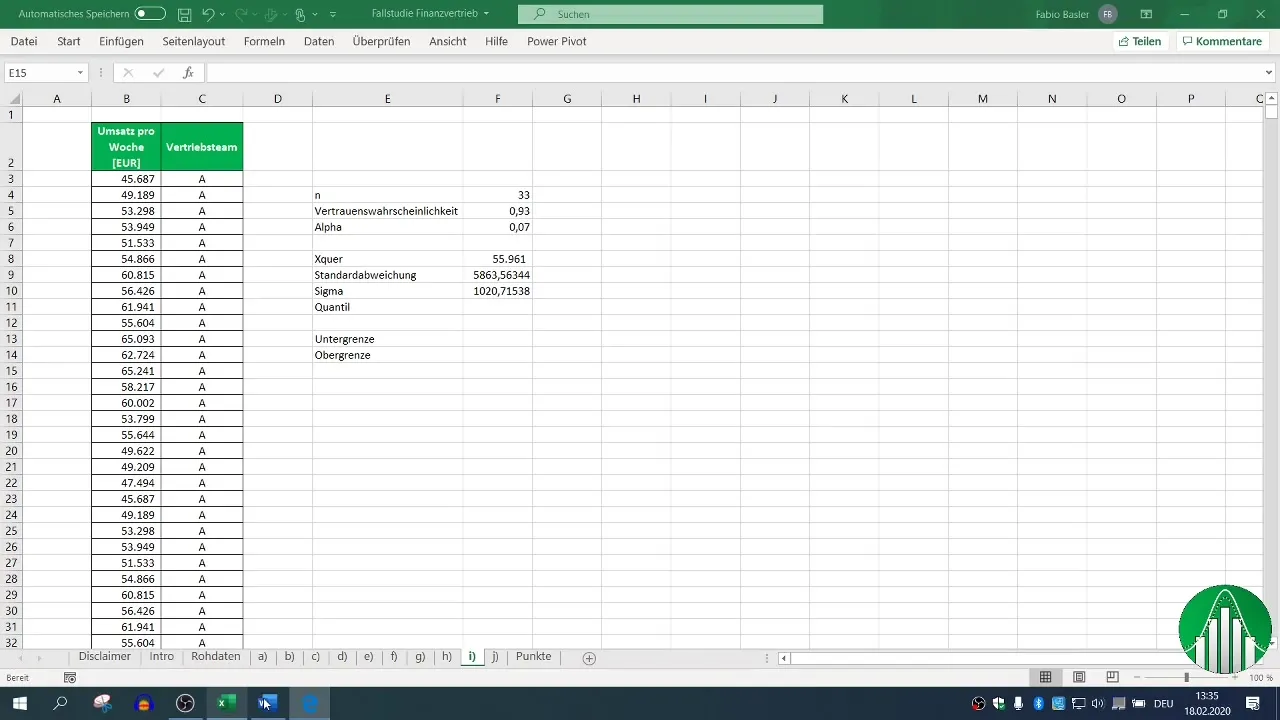
Step 6: Determining the Quantile

To calculate the two-sided confidence interval, you need the quantile. Since you specify a confidence probability of 93%, α is 7%, and you find the distribution of the quantile by using the Excel function.

Step 7: Calculating the Lower Limit

Now we calculate the lower limit of the confidence interval. Subtract the product of the quantile and the standard deviation of the mean from the mean (x̄).

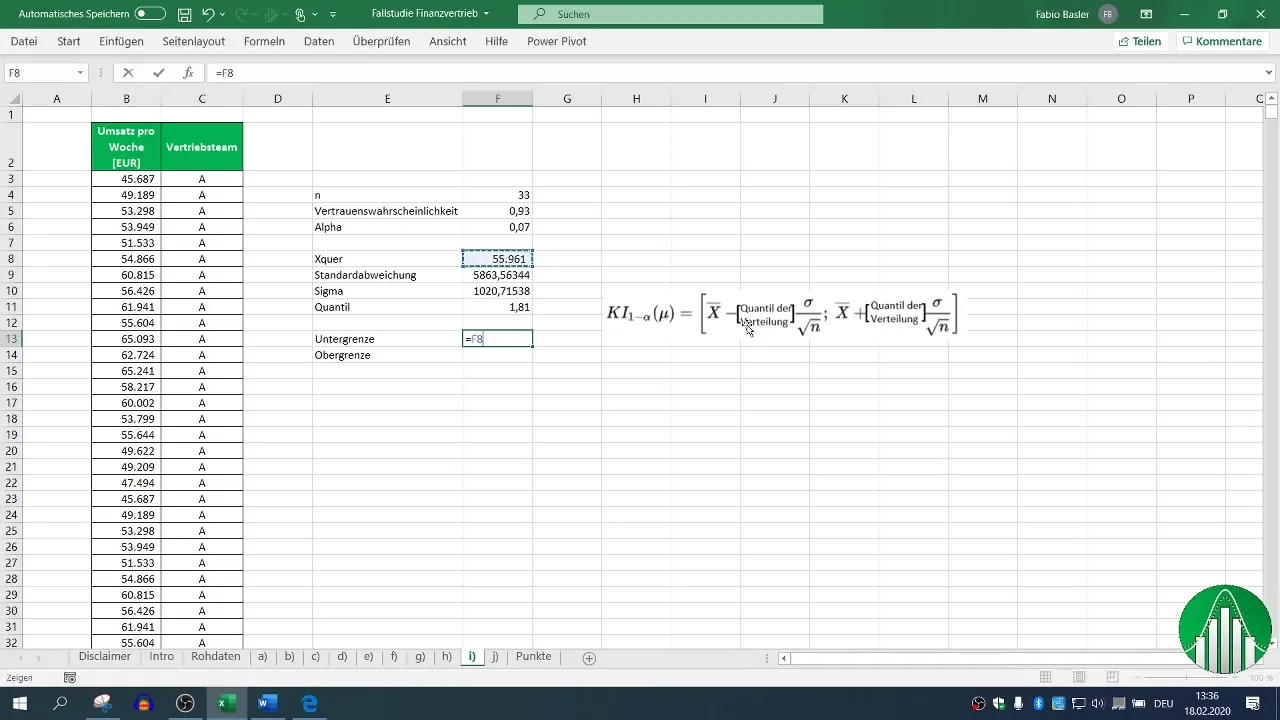
Step 8: Calculating the Upper Limit

The upper limit is calculated similarly, but you add the product instead of subtracting.

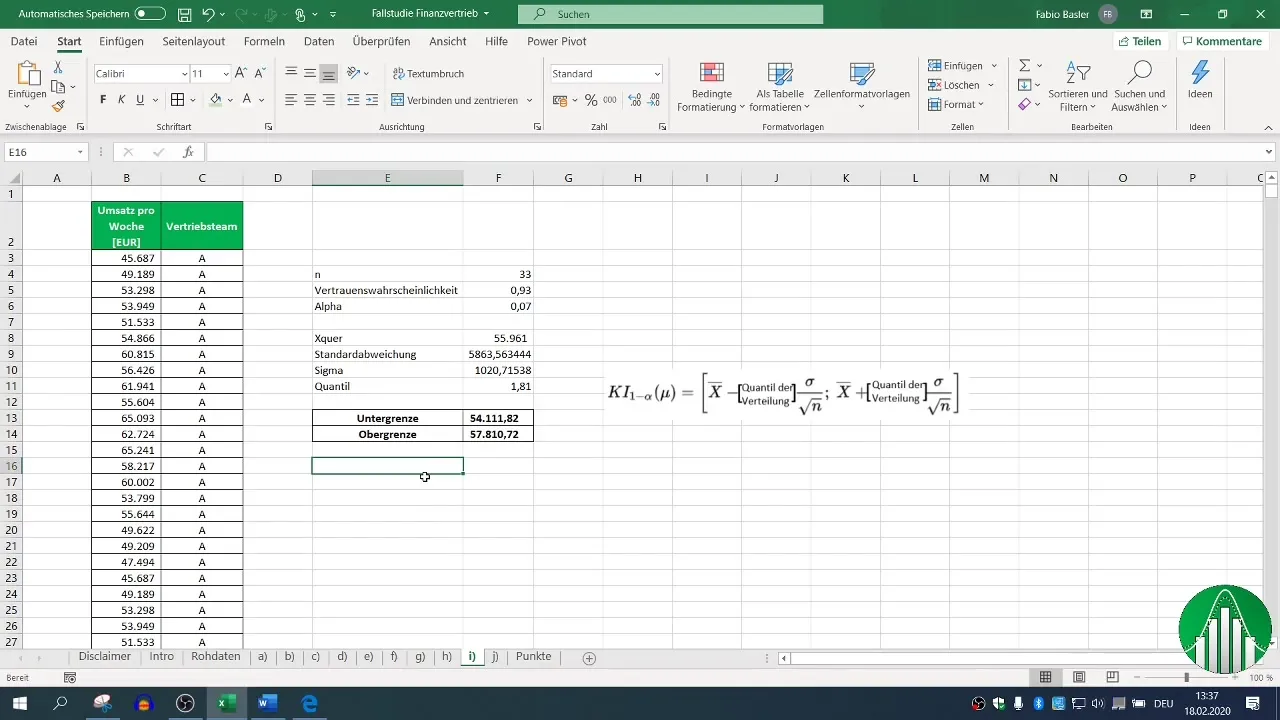
Step 9: Interpreting the Results

After these calculations, you will obtain the two-sided confidence interval for the weekly revenue of Sales Team A. In our example, the interval ranges from 54,111 to 57,810. This means that with a confidence probability of 93%, the true average revenue value lies within this range.

Summary

By accurately calculating the two-sided confidence interval, you can make precise statements about future revenue. You have learned how to prepare the relevant data, calculate the mean and standard deviation, and finally determine the interval boundaries. This method enables you to make data-driven decisions in your sales area.