La prueba t de dos muestras es una herramienta esencial en estadística cuando se quiere investigar la diferencia entre dos medias. En este tutorial aprenderás cómo realizar esta prueba de manera fácil y efectiva en Excel. A través de un ejemplo en biotecnología, aprenderás a comparar y analizar estadísticamente las tasas de éxito de dos empresas competidoras.
Principales conclusiones
- Aplicación de la prueba t de dos muestras para analizar la diferencia entre dos medias.
- Formulación y verificación de hipótesis.
- Uso de Excel para calcular y representar los resultados.
Guía paso a paso
Comenzamos creando los datos necesarios y realizando la prueba en Excel.
Paso 1: Preparar los datos
Empieza recolectando los datos brutos de las tasas de éxito de ambas empresas. Supongamos que tienes los datos de las empresas A y B, con una muestra de 100 registros por empresa.

Paso 2: Calcular el tamaño de la muestra y las medias
Crea una tabla en Excel para comparar las muestras y sus medias. Calcula el tamaño de la muestra (N) para ambas empresas, así como la media (X).

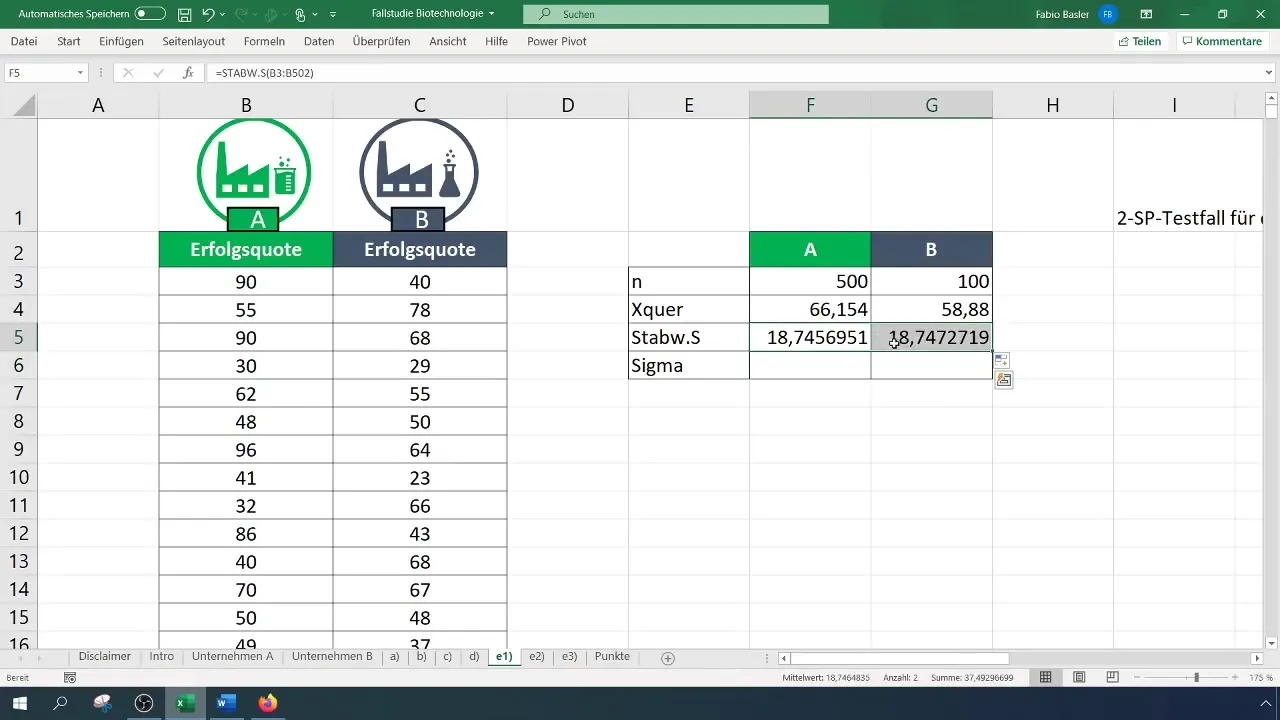
Paso 3: Calcular las desviaciones estándar
Calcula la desviación estándar para ambas empresas. Estos valores son importantes para calcular las variaciones y realizar los cálculos posteriores.
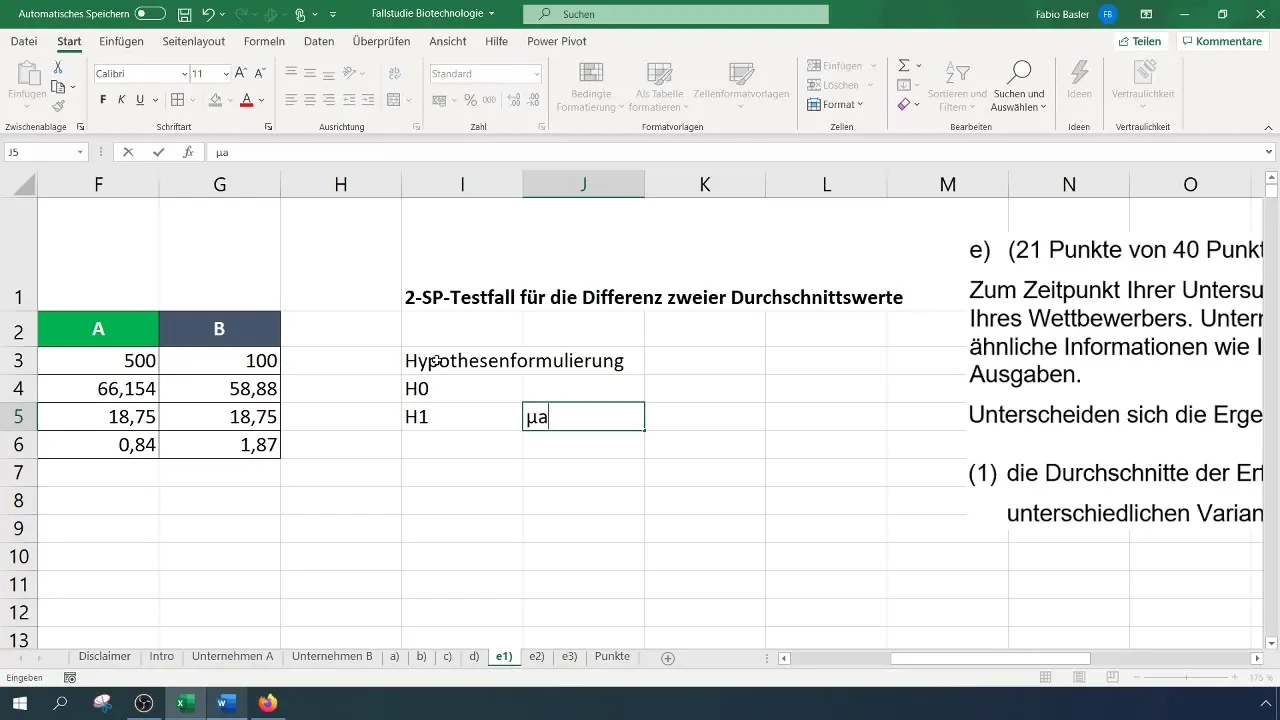
Paso 4: Formular hipótesis
Formula la hipótesis nula (H_0): Los valores promedio de las tasas de éxito de las empresas A y B son iguales. La hipótesis alternativa (H_1): Los valores promedio de las tasas de éxito son diferentes.
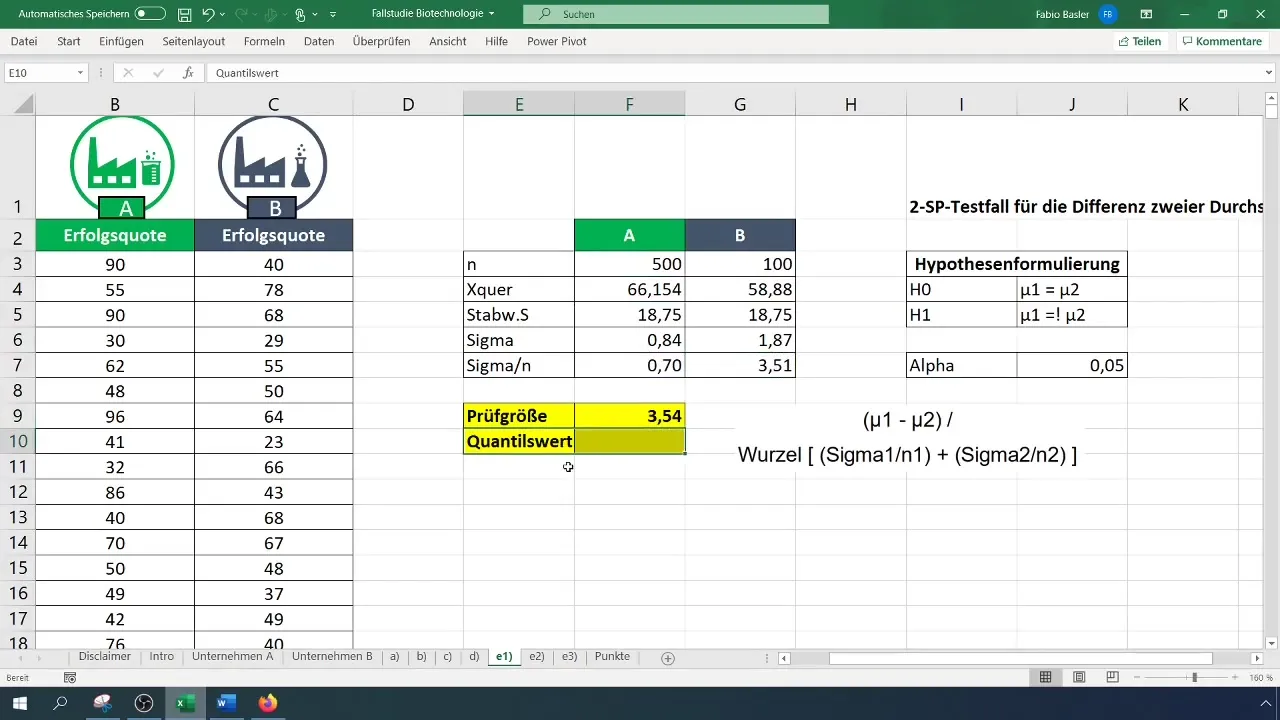
Paso 5: Calcular el estadístico de prueba
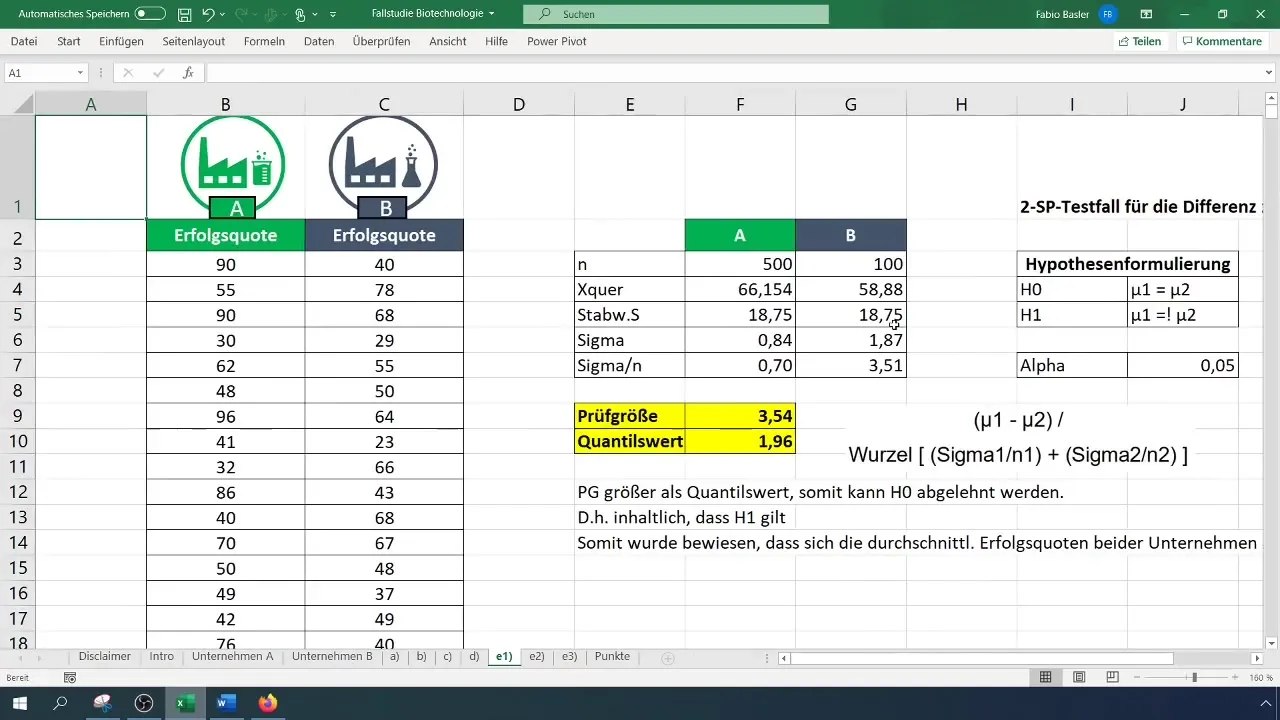
Para calcular el estadístico de prueba, utiliza la fórmula para la prueba t. Calcula la diferencia entre las medias y divídela por la raíz cuadrada de la suma de las varianzas de cada muestra.
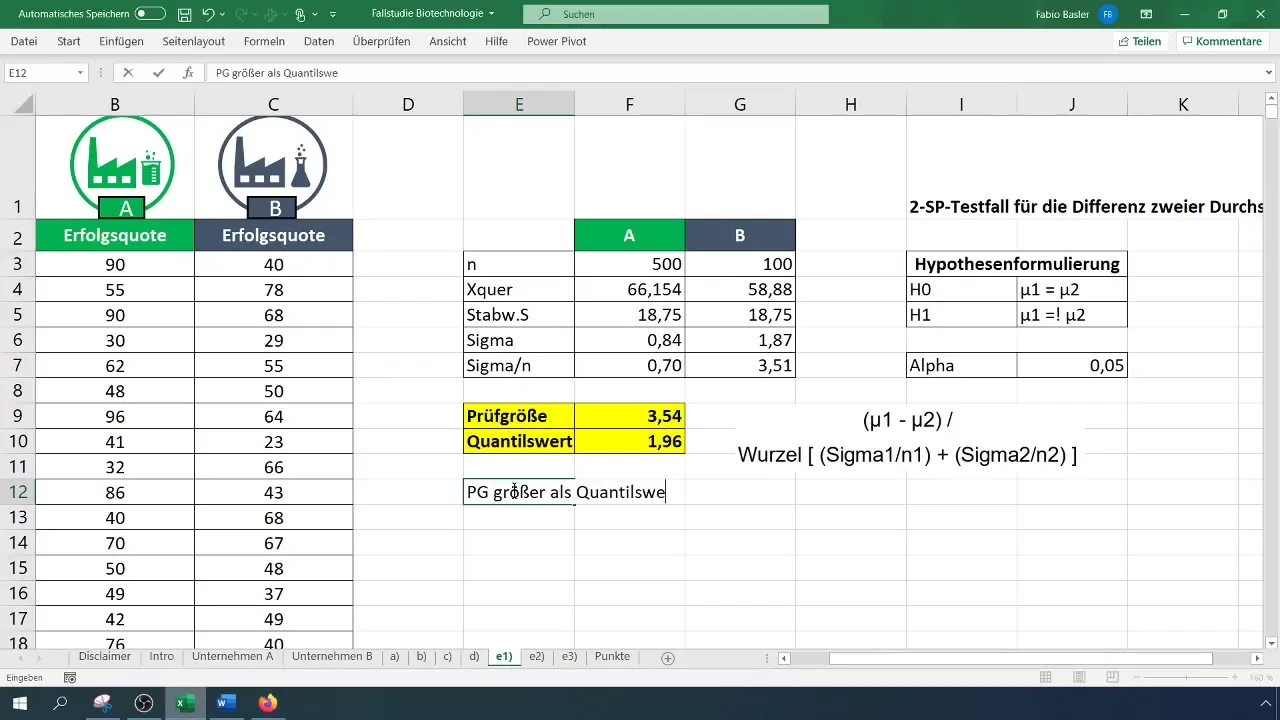
Paso 6: Calcular el valor crítico
Utiliza la distribución t de dos colas para encontrar el valor crítico. Establece el nivel alfa en 0,05. Consulta la tabla de distribución t o calcula el factor directamente en Excel.
Paso 7: Tomar una decisión sobre la hipótesis
Compara el estadístico de prueba calculado con el valor crítico. Si el estadístico de prueba es mayor que el valor crítico, rechaza la hipótesis nula (H_0) y confirma la hipótesis alternativa (H_1).
Paso 8: Interpretación de resultados
Por último, interpreta los resultados. En este ejemplo, se encontró que las tasas de éxito promedio de las dos empresas son significativamente diferentes.
Resumen
Has aprendido cómo realizar una prueba t de dos muestras en Excel para investigar las diferencias en las medias de dos grupos. Los pasos desde la preparación de datos hasta la interpretación de resultados son fundamentales para tomar decisiones válidas e informadas.
Preguntas frecuentes
¿Qué es una prueba t de dos muestras?Una prueba t de dos muestras compara las medias de dos grupos para determinar si son significativamente diferentes.
¿Cómo formulo hipótesis?La hipótesis nula (H_0) establece que las medias son iguales, mientras que la hipótesis alternativa (H_1) sugiere que son diferentes.
¿Cómo calculo el estadístico de prueba?El estadístico de prueba se calcula dividiendo la diferencia entre las medias por la raíz cuadrada de la suma de las varianzas.
¿Qué hago después de hacer los cálculos?Compara el estadístico de prueba con el valor crítico para decidir si rechazar la hipótesis nula.
¿Por qué es importante la desviación estándar?La desviación estándar ayuda a entender la variabilidad de los datos, siendo crucial para el cálculo del estadístico de prueba.


