Las pruebas estadísticas son un componente esencial del análisis de datos, especialmente cuando se trata de verificar diferencias entre grupos. Un procedimiento probado que se utiliza con frecuencia en la investigación y la economía es la prueba F de dos muestras. Esta guía te muestra paso a paso cómo realizar una prueba de este tipo con Excel para comparar las variables de gastos de investigación de dos empresas farmacéuticas.
Principales conclusiones
- Aprenderás cómo comparar la varianza de dos grupos utilizando una prueba F.
- La guía incluye pasos detallados para realizar la prueba en Excel, incluida la utilización de la función de análisis de datos.
- Al final, sabrás cómo interpretar los resultados y qué conclusiones sacar de ellos.
Instrucciones paso a paso
Paso 1: Preparar los datos
En primer lugar, necesitas los datos brutos de los gastos de investigación de ambas empresas. Abre tu archivo de Excel y copia los datos de investigación respectivos de las dos empresas en columnas separadas.

Paso 2: Calcular el tamaño de la muestra y la varianza
El tamaño de la muestra es de 500 para la empresa A y 100 para la empresa B. Para calcular la varianza de los datos, utiliza la función VAR.S() para estimar la varianza de los grupos. Asegúrate de introducir los valores en formato Excel para obtener resultados precisos.
Paso 3: Formular hipótesis
Para la prueba F, las hipótesis se definen de la siguiente manera:
- Hipótesis nula (H0): σ1² = σ2² (Las varianzas de las dos empresas son iguales).
- Hipótesis alternativa (H1): σ1² ≠ σ2² (Las varianzas de las dos empresas son diferentes).
Paso 4: Calcular el estadístico de prueba
Calcula el estadístico de prueba (F-estadístico) dividiendo las dos varianzas. Utiliza la fórmula Varianza_A / Varianza_B. Si has introducido correctamente las varianzas, obtendrás un estadístico F para comparar.
Paso 5: Determinar el valor crítico
Para determinar el valor F crítico, necesitas el nivel alfa (normalmente 0,05) y los grados de libertad. Los grados de libertad se calculan de la siguiente manera: df1 = n1 - 1 y df2 = n2 - 1. Calcula el valor crítico con la función F.INV().

Paso 6: Tomar una decisión
Compara el estadístico F calculado con el valor F crítico. Si el estadístico F es mayor que el valor crítico, rechaza la hipótesis nula, de lo contrario, no lo hagas. En este ejemplo, el criterio para el rechazo es que el estadístico de prueba debe ser menor que el valor cuantil (F crítico).

Paso 7: Utilizar el análisis de datos de Excel
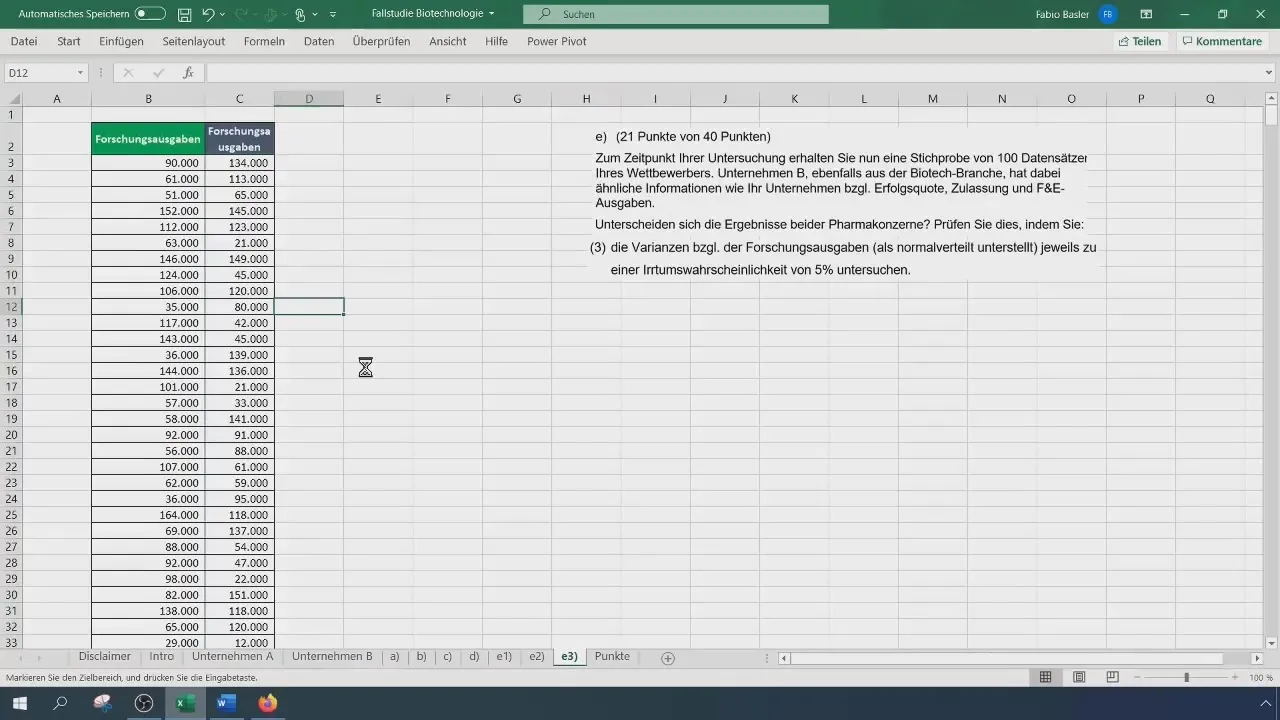
Excel también ofrece la posibilidad de realizar la prueba F a través de la función de análisis de datos. Ve a "Datos" y selecciona "Análisis de datos". Elige "Prueba F de dos muestras". Ingresa los rangos de las dos variables y selecciona las opciones correspondientes.
Paso 8: Interpretar los resultados
Analiza los resultados de la prueba F. Si el estadístico F calculado y el valor p en la salida de Excel dan los mismos resultados que tu cálculo manual, puedes concluir que las varianzas de las dos empresas son iguales.
Resumen
La prueba F de dos muestras es una herramienta esencial en el análisis estadístico que te permite comparar diferencias de varianza entre dos grupos. En esta guía has aprendido cómo llevar a cabo esta prueba de manera efectiva en Excel, desde la preparación de los datos hasta la interpretación de los resultados.
Preguntas frecuentes
¿Qué es la prueba F de dos muestras?La prueba F de dos muestras compara las varianzas de dos grupos para determinar si son estadísticamente significativamente diferentes.
¿Cuándo debo utilizar una prueba F?Se utiliza una prueba F cuando deseas comprobar la igualdad de varianzas en dos grupos independientes.
¿Cómo se calcula la estadística F?La estadística F se calcula dividiendo la varianza del primer grupo entre la varianza del segundo grupo.
¿Qué debo hacer si se rechaza la hipótesis nula?Si se rechaza la hipótesis nula, puedes asumir que las varianzas de los dos grupos son significativamente diferentes desde el punto de vista estadístico.
¿Existen alternativas a la prueba F?Sí, también puedes utilizar el test de Bartlett o el test de Levene si deseas probar la homogeneidad de varianzas.


