La capacidad de usar herramientas de análisis de datos en Excel es crucial para el éxito en los negocios y las ventas. Esta guía se centra en el análisis de correlación y regresión para determinar cómo el número de empleados y la cantidad de llamadas telefónicas afectan las cifras de ventas. Realizar ambos análisis te ayudará a evaluar cuantitativamente estas relaciones y hará que la interpretación de los resultados sea comprensible.
Principales Conclusiones
- Diferencia entre correlación y regresión: la correlación muestra la relación entre dos variables, mientras que la regresión analiza el impacto de varias variables independientes en una variable dependiente.
- Visión de la significancia estadística y calidad del modelo.
- Evaluación cuantitativa de la importancia de los regresores.
Guía paso a paso
1. Preparación para el análisis de datos
Antes de comenzar el análisis, asegúrate de que tus datos estén correctamente preparados en Excel. Importa los datos sobre ventas, número de empleados y llamadas a una hoja de cálculo de Excel. Verifica que todos los registros estén completos y que las variables necesarias estén presentes.

2. Realización del análisis de correlación
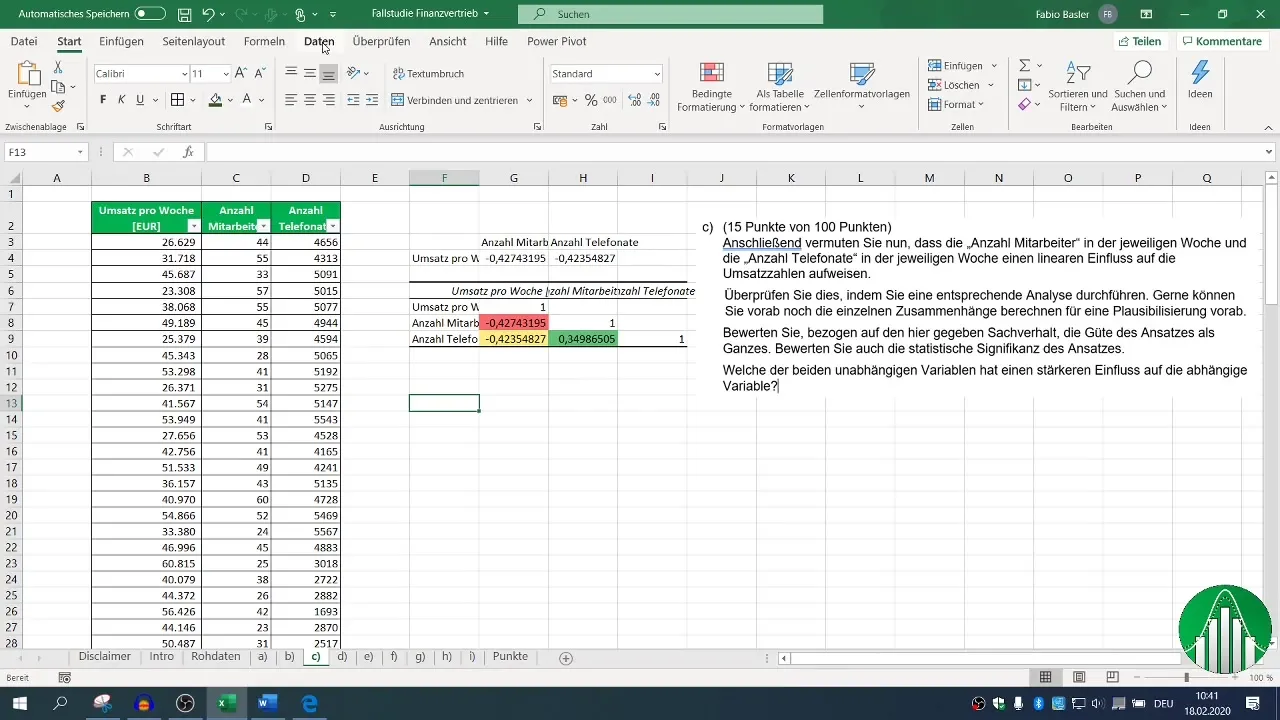
Para analizar la correlación entre las variables de ventas, empleados y llamadas, puedes calcular el coeficiente de correlación. Para esto, utiliza la fórmula =CORREL() en Excel. Para obtener una vista general de todas las variables, crea una matriz de correlación.
Selecciona primero las columnas correspondientes a las ventas y al número de empleados. Con la fórmula =CORREL(), señala las áreas de ventas y el número de empleados. El resultado mostrará la fuerza de la relación.
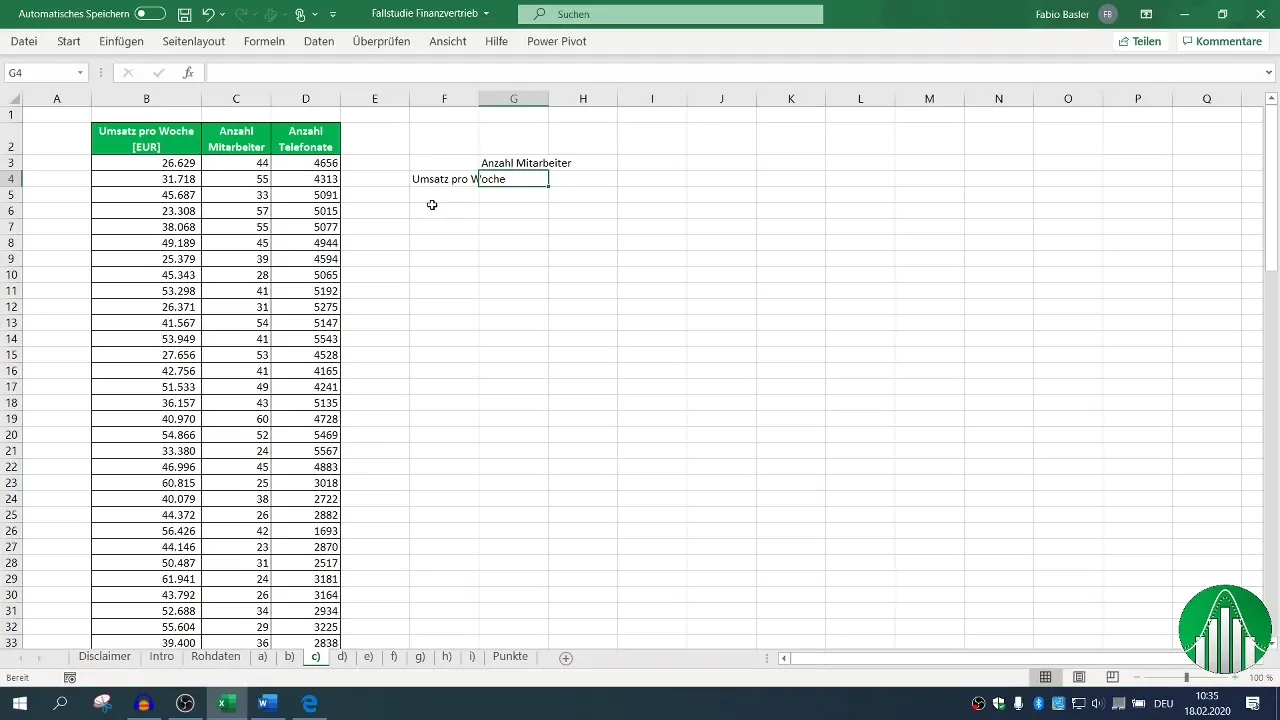
3. Creación de una matriz de correlación
Para un análisis más completo, se recomienda utilizar las funciones de análisis de datos de Excel. Activa la función de análisis de datos si aún no lo has hecho. Ve a la pestaña "Datos", haz clic en "Análisis de datos" y selecciona "Correlación".
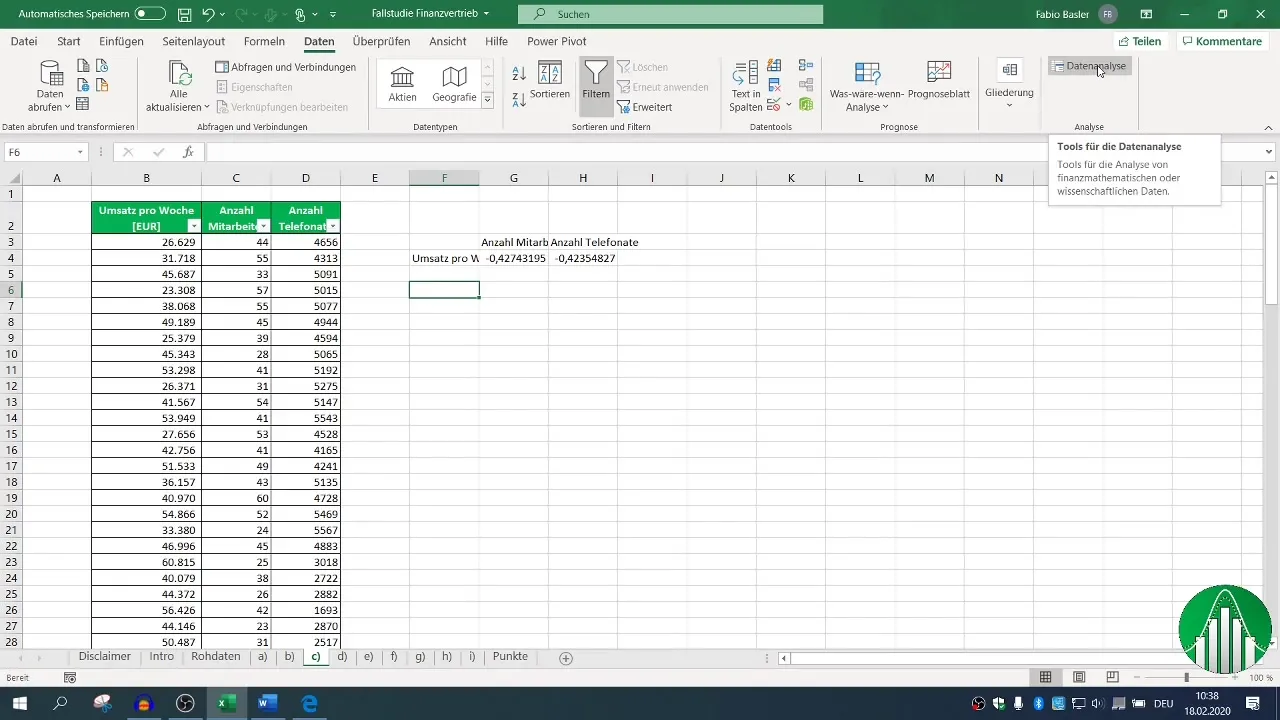
Define el rango de entrada para tus datos y marca la casilla para encabezados, para que Excel reconozca correctamente las etiquetas. Después de establecer el rango de salida, podrás generar la matriz de correlación que mostrará todas las relaciones relevantes.
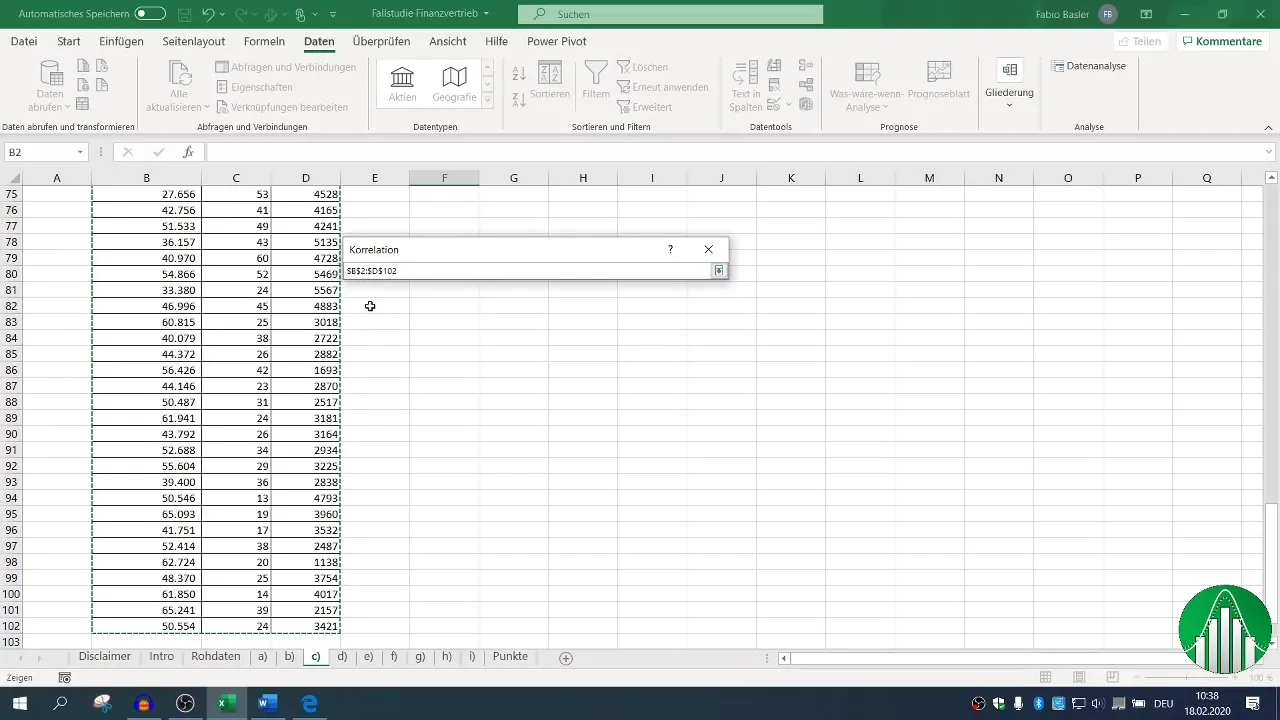
4. Visualización de las correlaciones
Para hacer los resultados más visuales, puede ser útil una representación gráfica mediante un gráfico XY. Selecciona tus datos de X e Y y genera el diagrama de dispersión.
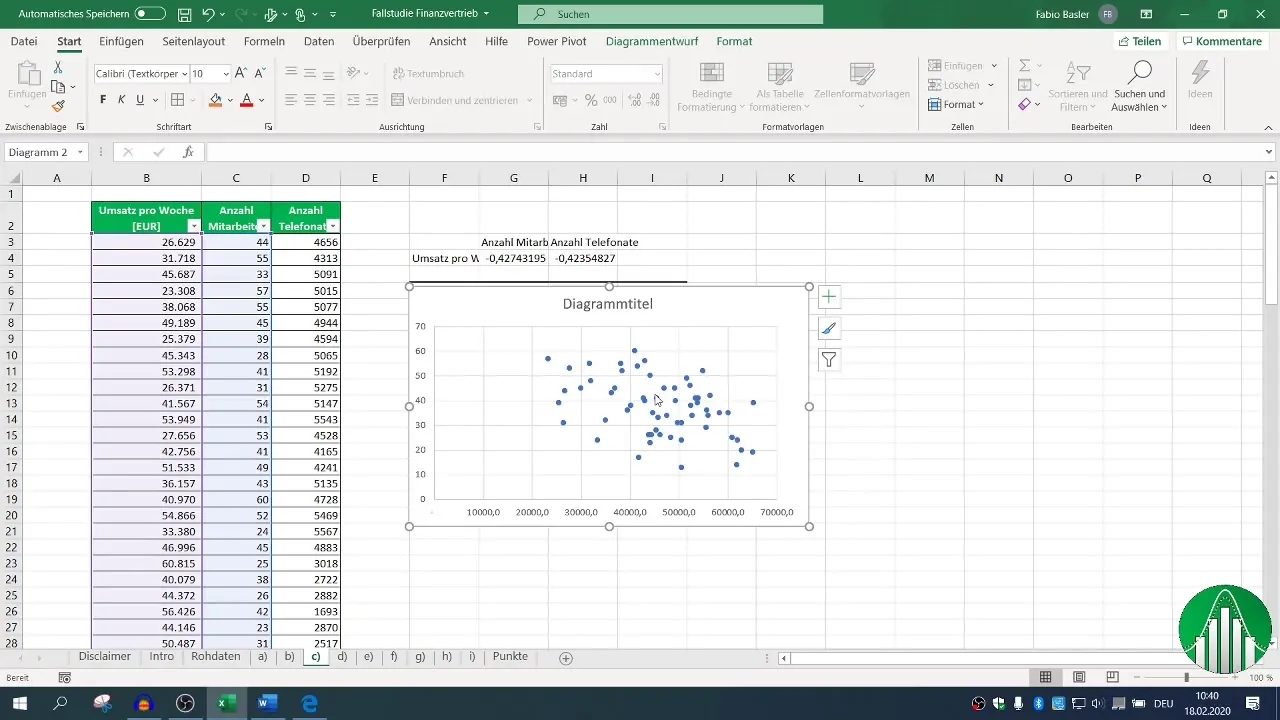
Añade una línea de tendencia para representar visualmente la relación, lo que puede ofrecer una comprensión más intuitiva de los datos.
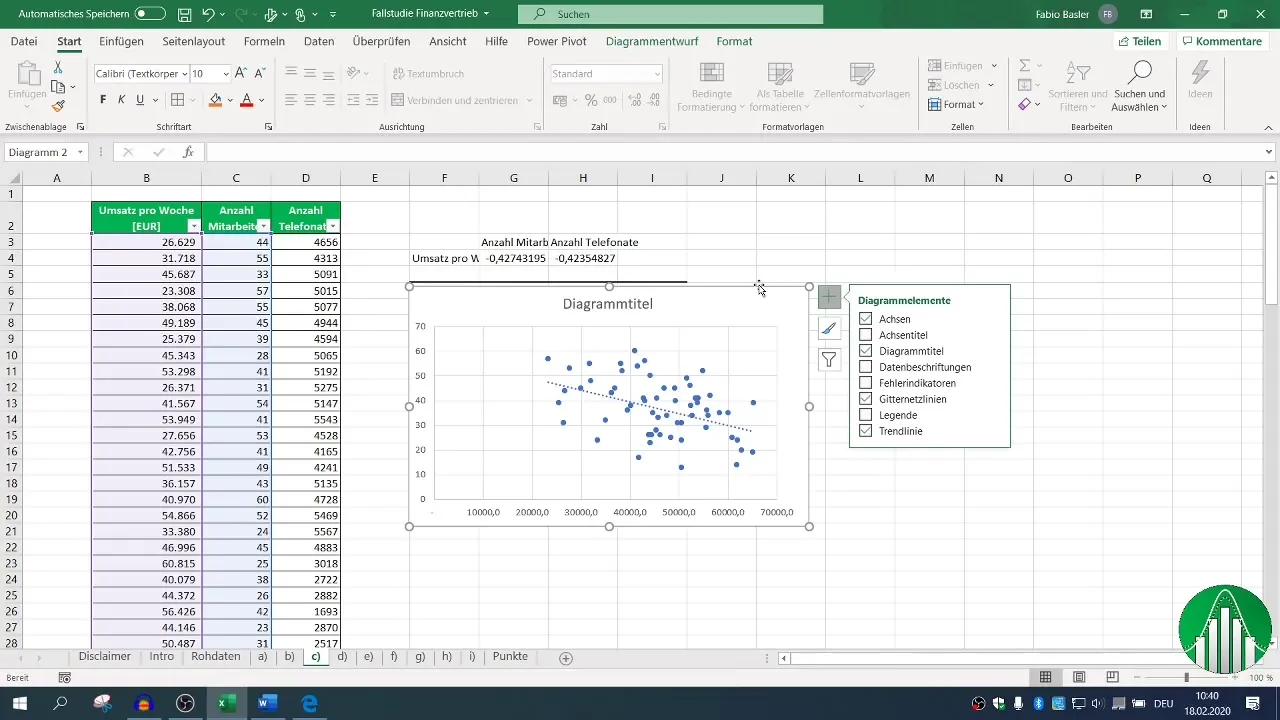
5. Realización del análisis de regresión
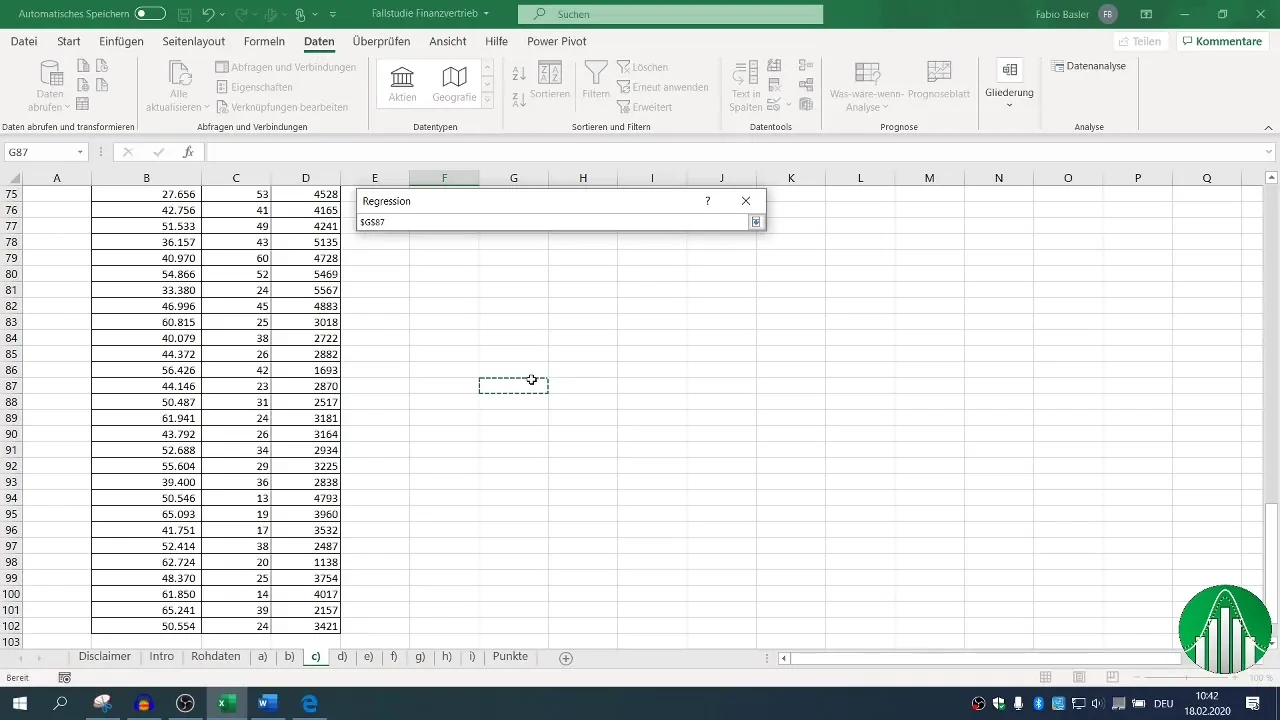
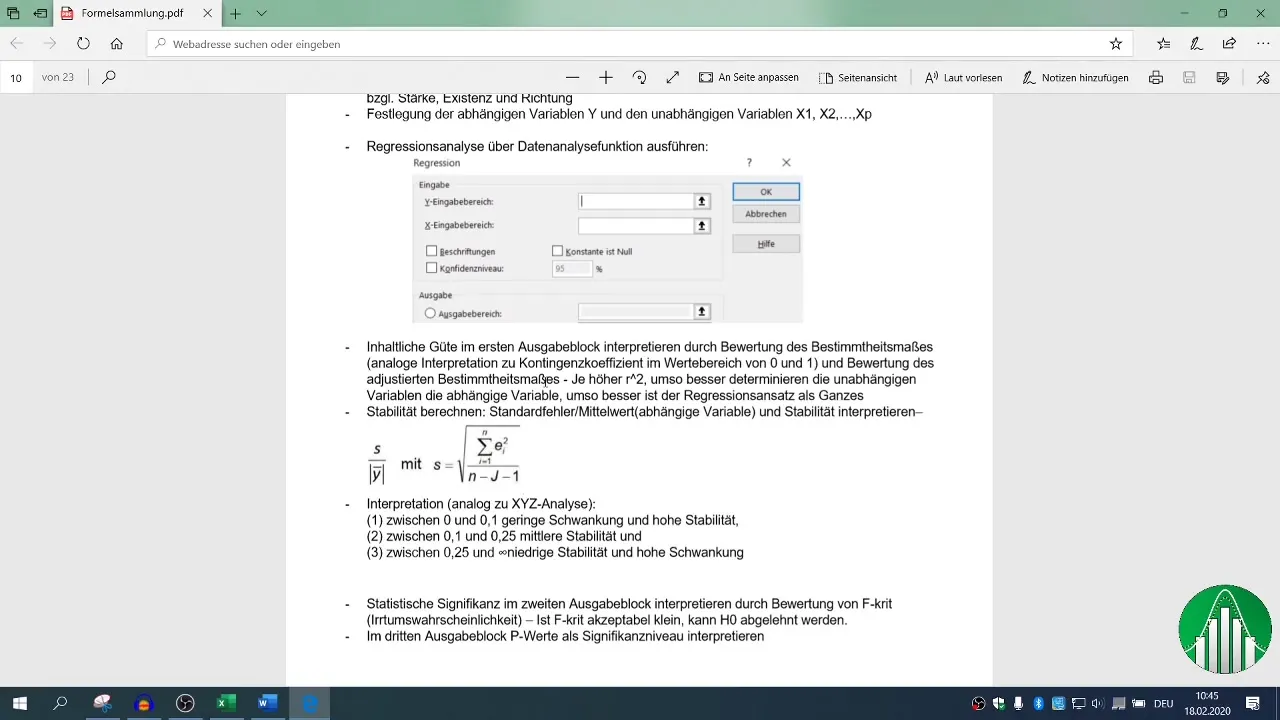
Luego sigue el paso del análisis de regresión. Ve nuevamente a "Datos" y selecciona "Análisis de datos", luego "Regresión". Aquí puedes definir para el rango de entrada la variable dependiente (ventas) y las variables independientes (número de empleados y llamadas).
Asegúrate de tener configurado el encabezado para los valores y define tu rango de salida. El nivel de confianza estándar está establecido en 95%, lo cual es adecuado para la mayoría de análisis.
6. Evaluación del análisis de regresión
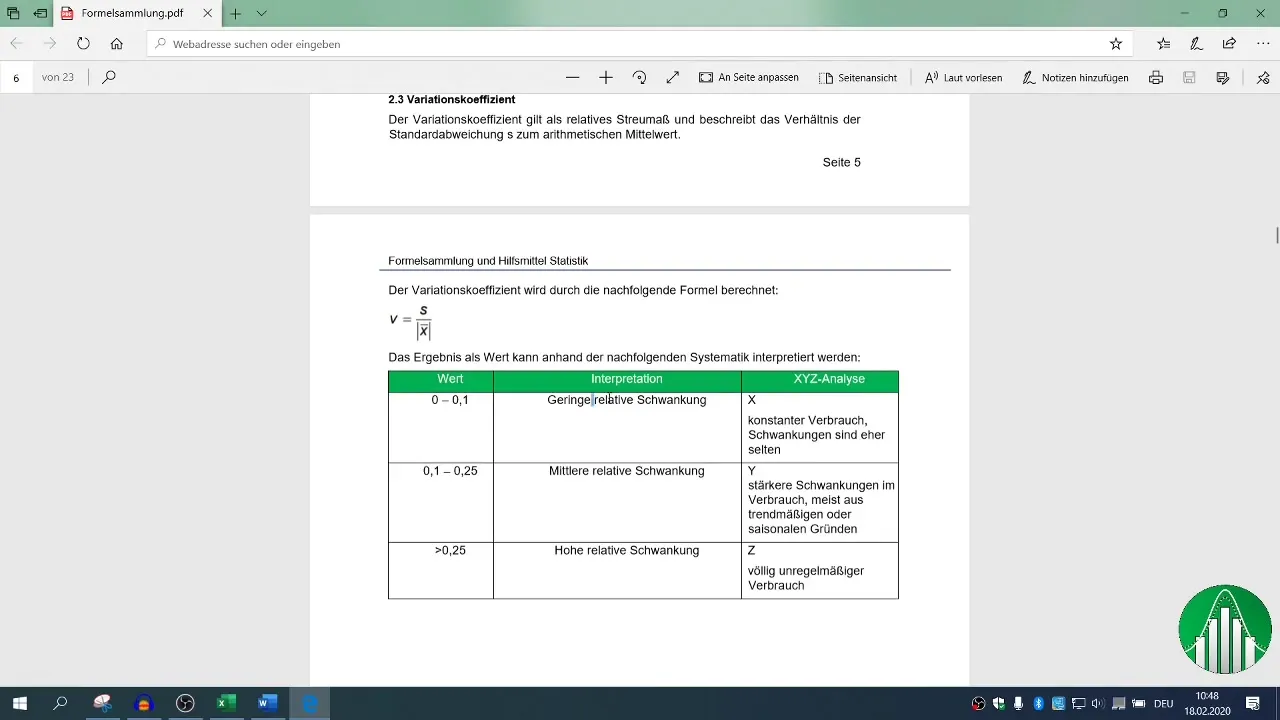
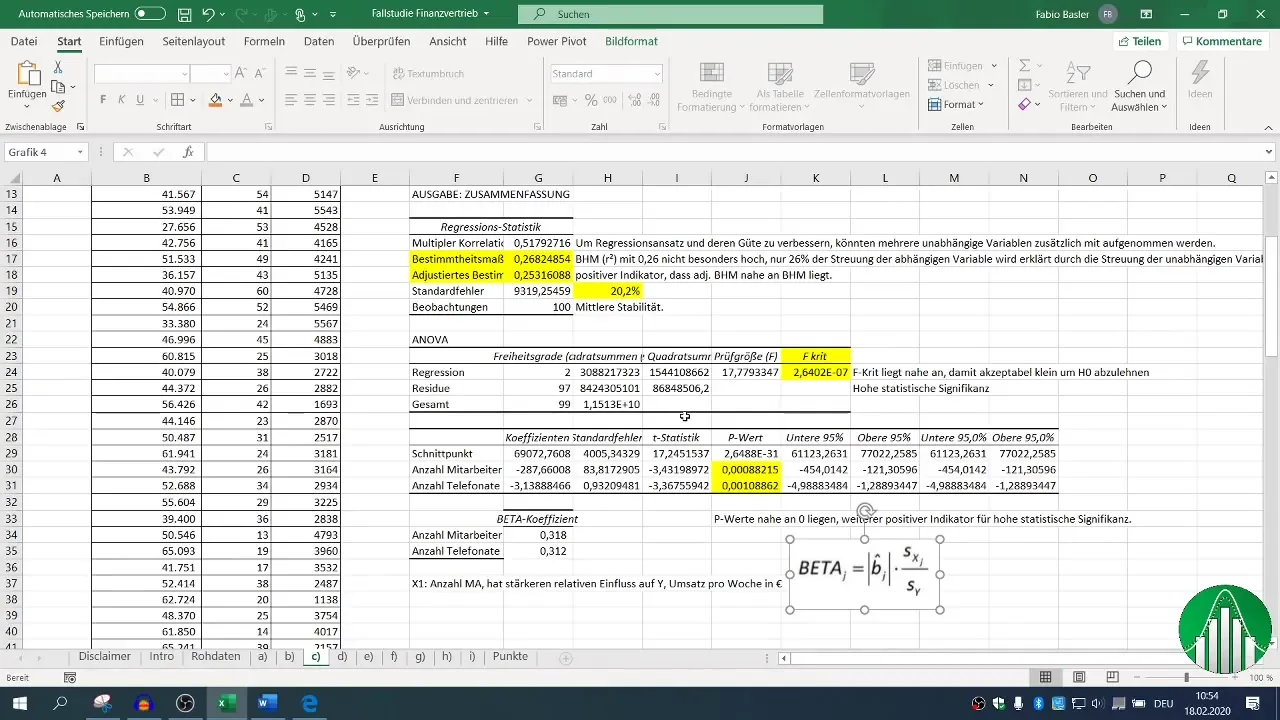
Después de realizar la regresión, tendrás varios bloques de salida disponibles. Concéntrate en la medida de determinación (R²), que describe la calidad del modelo. Un R² de 0,26 indica que solo el 26% de la variabilidad de las ventas se explica mediante las variables independientes.
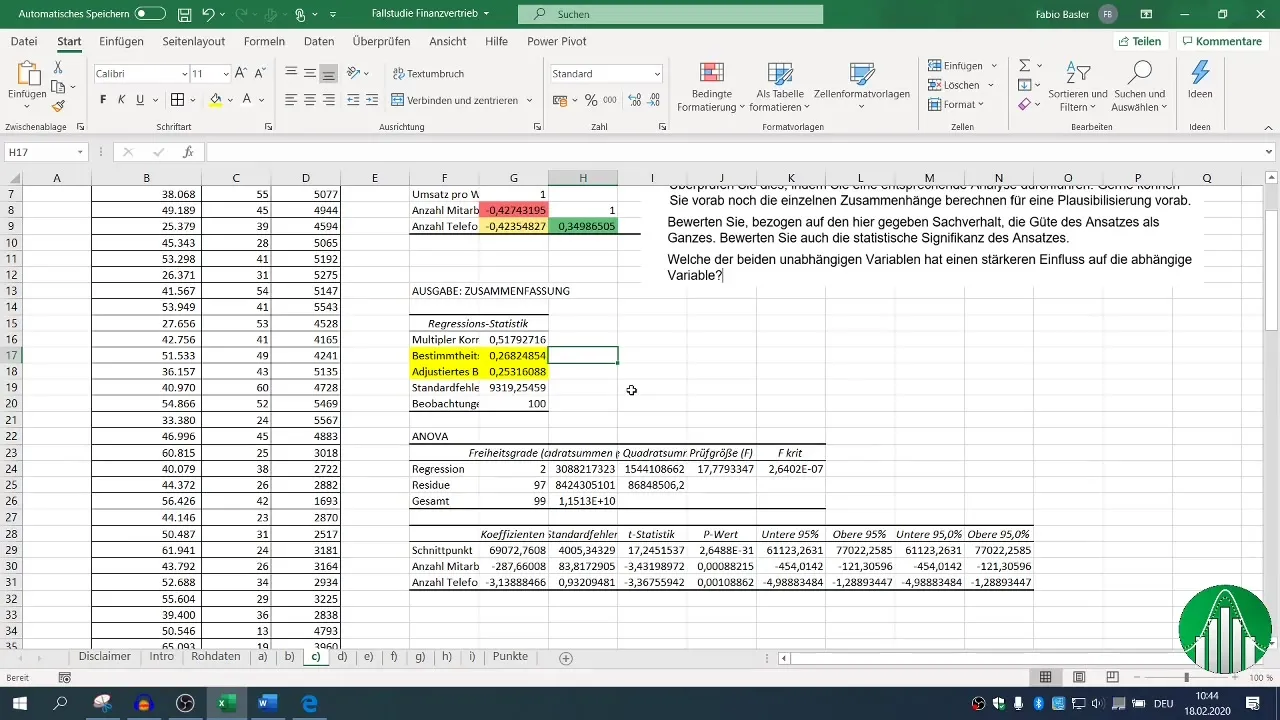
El coeficiente de determinación ajustado debería estar cerca de R², lo cual en este caso es un indicador positivo.
7. Evaluación de la significancia estadística
El valor F y los valores p de las variables independientes son cruciales para evaluar la significancia estadística de tu modelo. Un valor p por debajo de 0,05 indica que la relación es estadísticamente significativa.
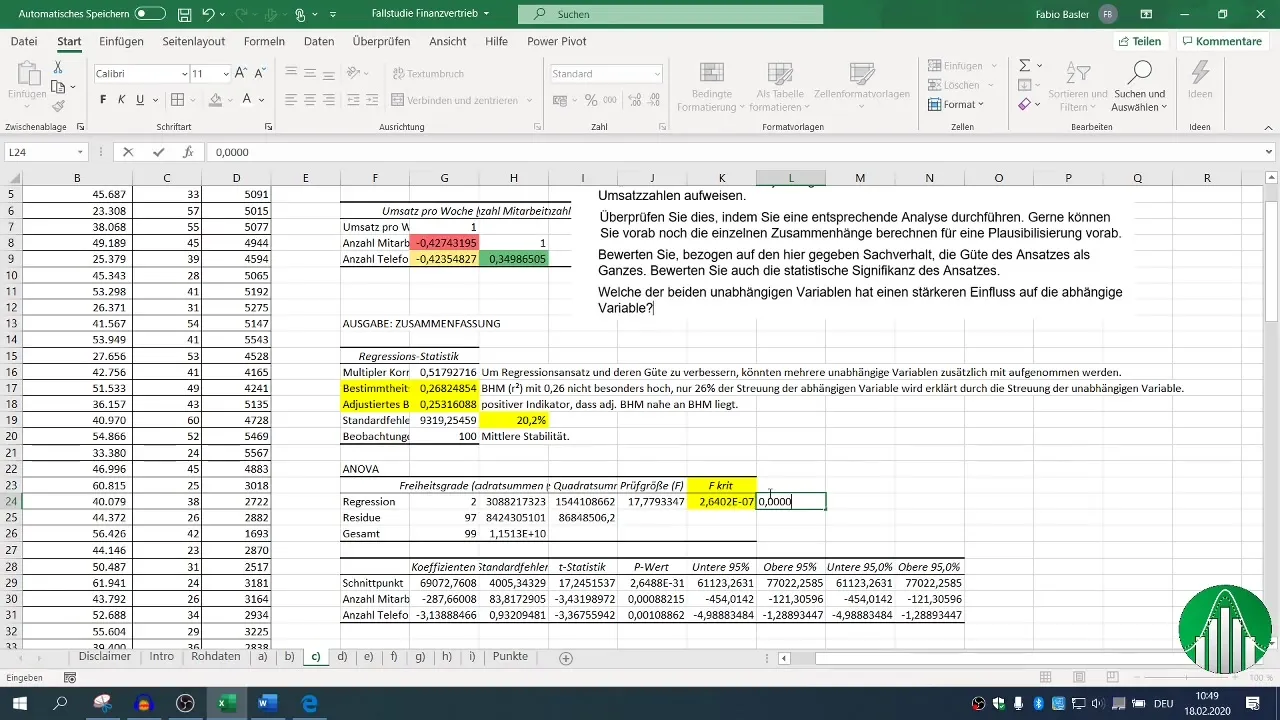
Evaluar estos parámetros estadísticos en relación con R² te ayuda a comprender la estabilidad y la validez de tus resultados.
8. Comparación de los factores de influencia
Finalmente, te interesa saber qué factor - número de empleados o llamadas telefónicas - tiene una influencia más fuerte en las ventas. Para ello, recurres a los coeficientes beta y los comparas.
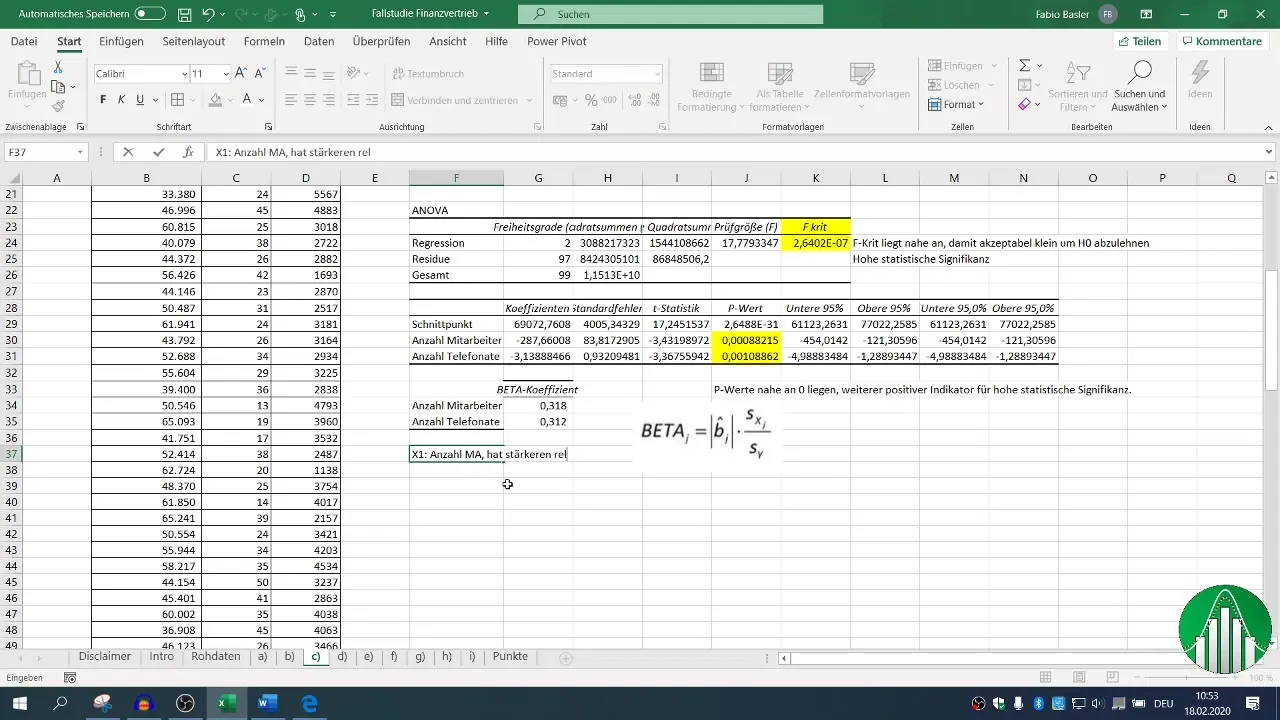
Un coeficiente beta más alto muestra la influencia relativa; quizás descubras que el número de empleados tiene una mayor influencia en las ventas que la cantidad de llamadas telefónicas.
Resumen
El análisis anterior te ha proporcionado información valiosa sobre las relaciones estadísticas entre las variables de ventas, número de empleados y llamadas telefónicas. Al realizar análisis de correlación y regresión de forma sistemática en Excel, puedes tomar decisiones fundamentadas basadas en tus resultados.
Preguntas frecuentes
¿Por qué es importante un análisis de correlación?Un análisis de correlación ayuda a identificar la relación entre dos variables antes de realizar un análisis de regresión detallado.
¿Cómo interpreto R² en un análisis de regresión?Un R² de 0,26 significa que el 26 % de las variaciones en la variable dependiente (ventas) son explicadas por las variables independientes.
¿Cuál es la diferencia entre correlación y regresión?La correlación mide la relación entre dos variables, mientras que la regresión evalúa el efecto de varias variables independientes en una variable dependiente.
¿Cómo puedo probar la significancia estadística?Pruebas la significancia estadística a través del valor p; los valores p por debajo de 0,05 se consideran significativos.
¿Qué papel juegan los coeficientes beta?Los coeficientes beta muestran la influencia relativa de las variables independientes en la variable dependiente.


