Las pruebas de hipótesis estadísticas son una herramienta indispensable para las empresas a la hora de tomar decisiones fundamentadas. En la siguiente sección te mostraremos cómo realizar una prueba F de dos muestras en Excel para verificar la validez de tus hipótesis sobre la varianza de tus datos de ventas. Esta guía te acompañará paso a paso en el proceso para que puedas aplicar las técnicas aprendidas con seguridad.
Principales conclusiones
- La prueba F de dos muestras se utiliza para comparar las varianzas de dos grupos de datos.
- El objetivo es verificar si la varianza de los datos de ventas actuales difiere de un valor supuesto.
- Excel proporciona las herramientas necesarias para realizar los cálculos y comparaciones requeridas.
Guía paso a paso
1. Preparación de los datos
Antes de comenzar la prueba, asegúrate de que tus datos estén preparados. Es importante eliminar los filtros para considerar todos los datos relevantes. Comienza seleccionando los datos en las columnas correspondientes.

2. Definición de los parámetros
Define los parámetros para tu prueba. Debes saber cuántos puntos de datos estás analizando. En nuestro ejemplo, asumimos que tienes 100 números de ventas que siguen una distribución normal.

3. Registro del valor de varianza anterior
El valor conocido de varianza o ventas anteriores juega un papel central en tu análisis. En este ejemplo, el valor anterior es de 116 millones de euros por semana.
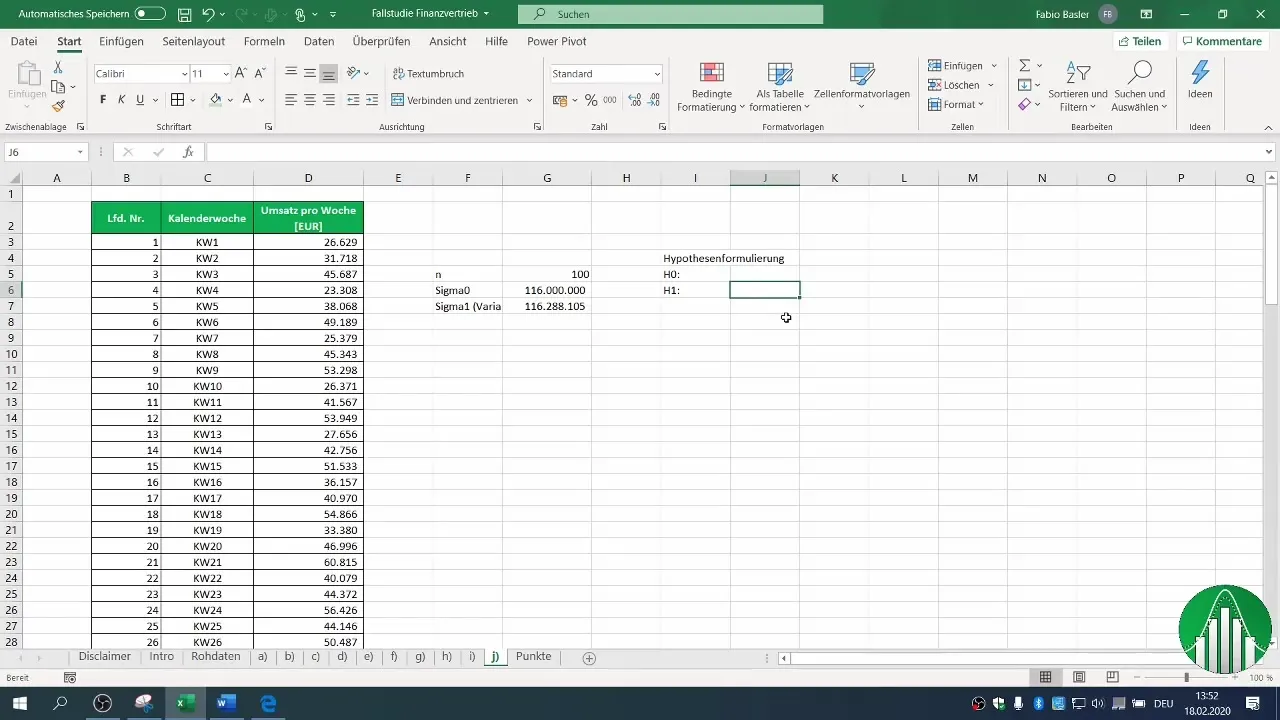
4. Formulación de hipótesis
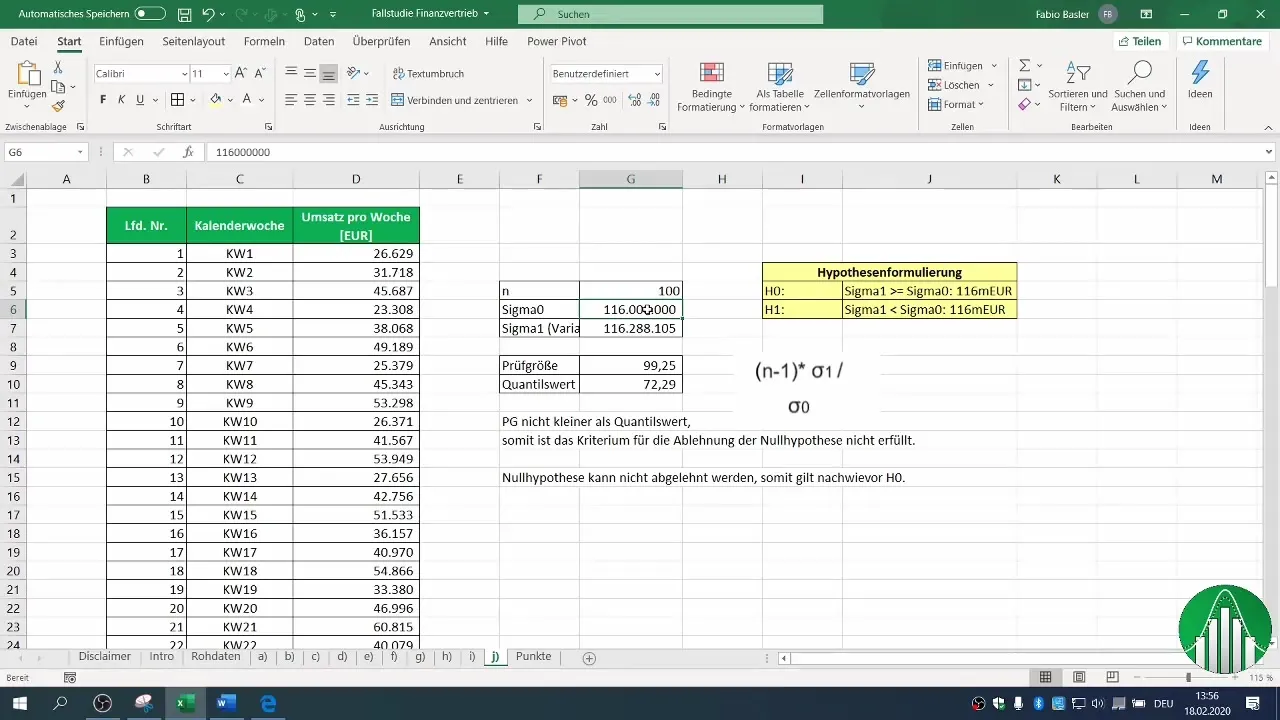
Formula tu hipótesis nula (H0) y alternativa (H1). En este caso, H0 afirma que la varianza permanece igual o mayor que 116 millones, mientras que H1 sugiere que la varianza ha disminuido.
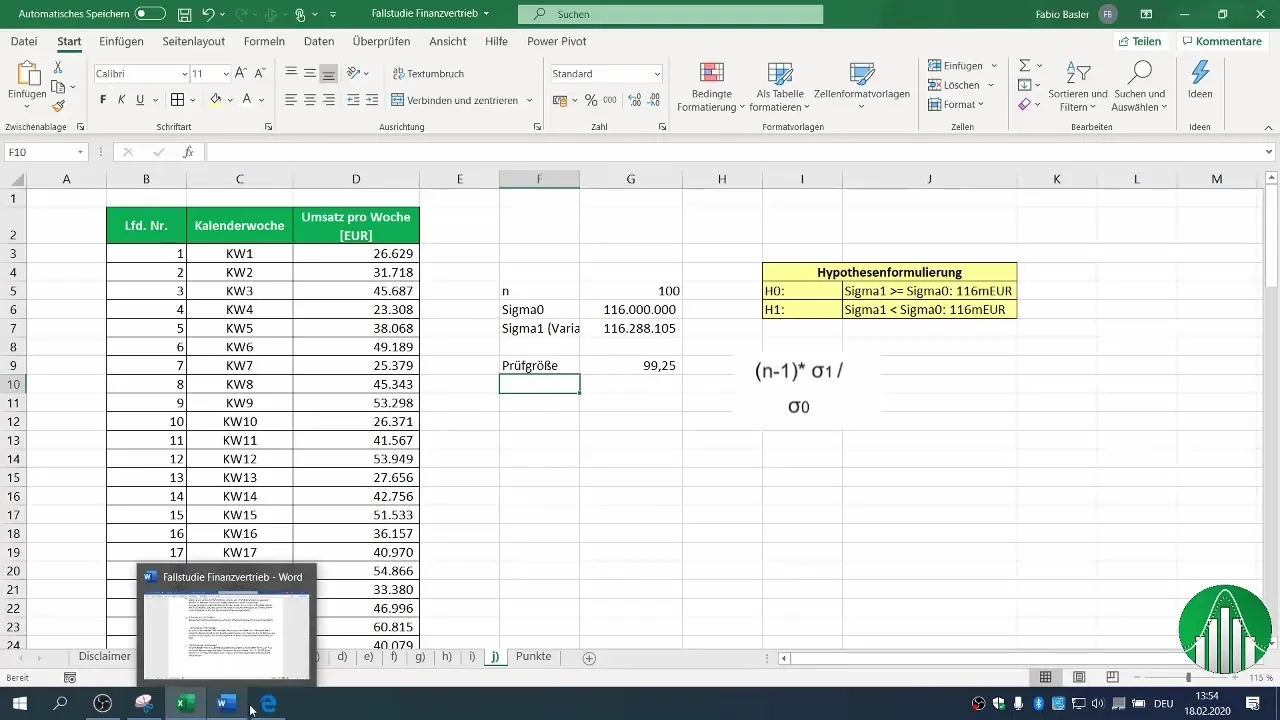
5. Cálculo del estadístico de prueba
El estadístico de prueba se puede calcular utilizando la varianza de tu muestra. Realiza los cálculos necesarios para determinar el valor de tu estadístico de prueba. Se calcula mediante la fórmula: (n-1) * σ1 / σ0, donde σ1 es la varianza de tu muestra y σ0 es la varianza anterior.
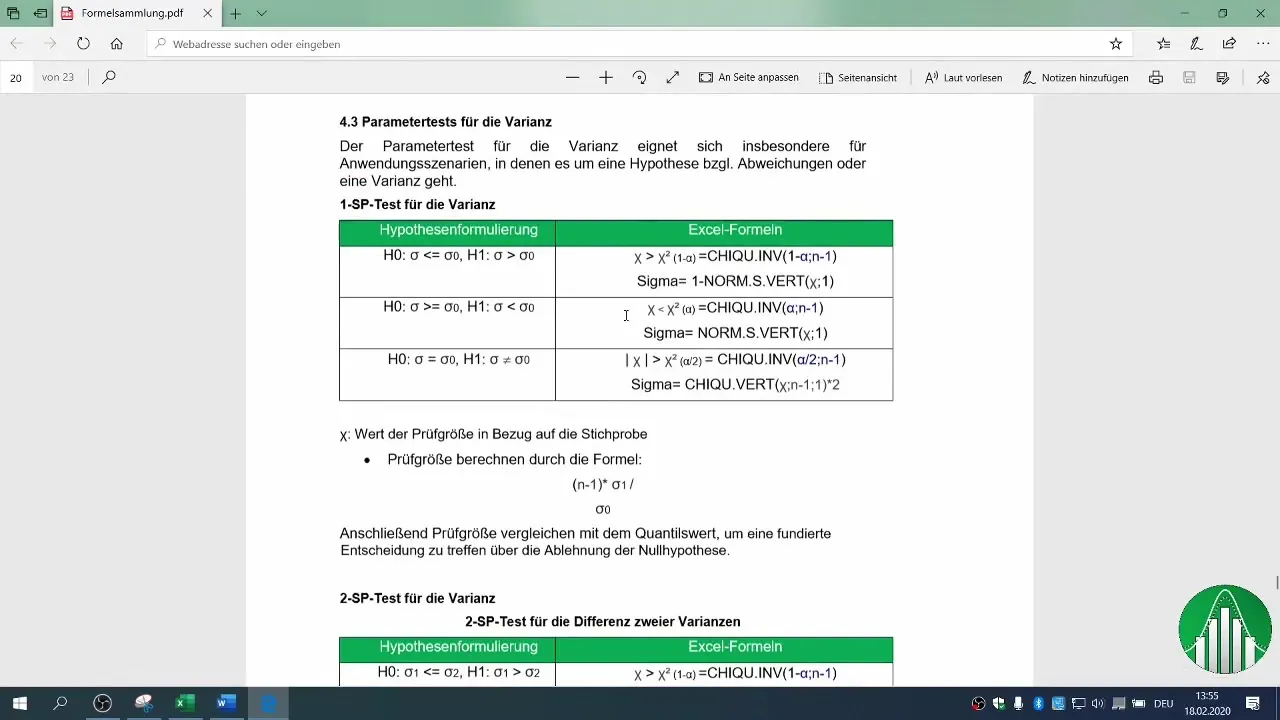
6. Determinación de la región crítica
Para decidir si puedes rechazar la hipótesis nula, debes definir la región crítica. Utiliza la tabla de distribución Ji-cuadrado para tu nivel de confianza. En nuestro ejemplo, hemos utilizado una probabilidad de error del 2%.
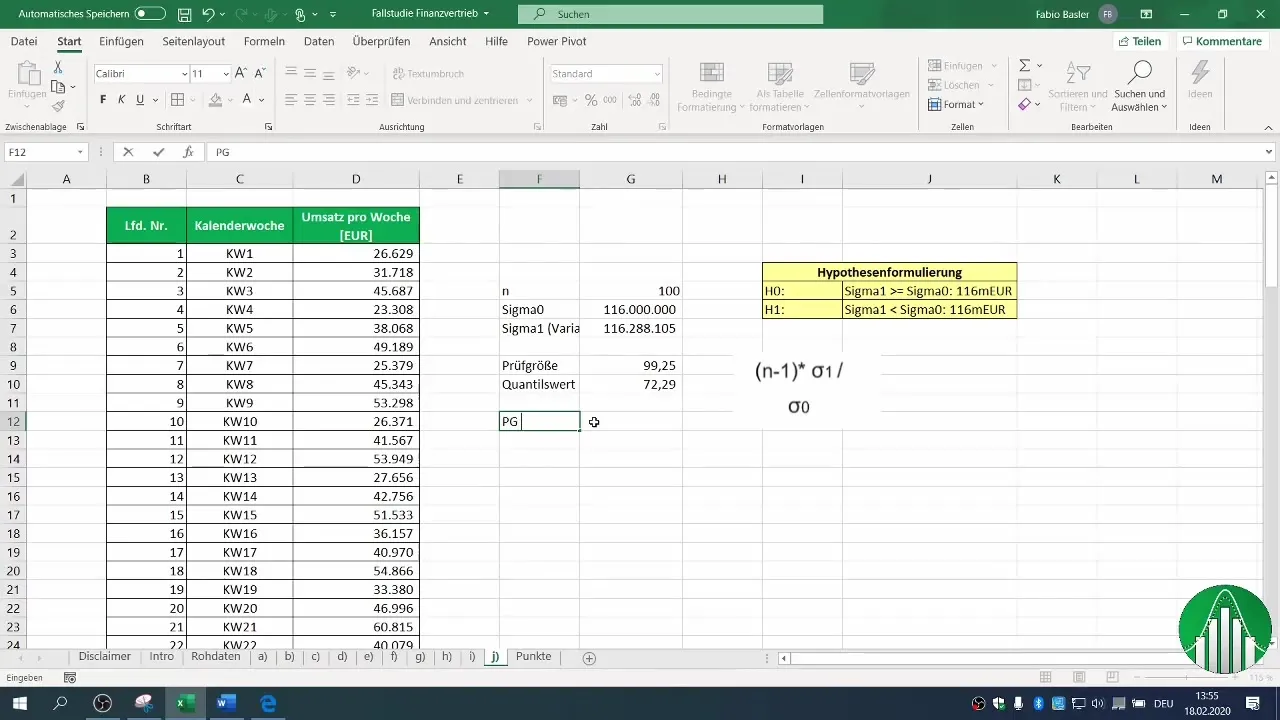
7. Comparación del estadístico de prueba y el valor crítico
Ahora verifica si tu estadístico de prueba calculado es menor que el valor crítico. En este caso, hemos determinado que nuestro estadístico de prueba no es menor que el valor crítico de la distribución.
8. Conclusión
Basándote en tu comparación, ahora puedes decidir si rechazar o no la hipótesis nula. En nuestro ejemplo, encontramos que la hipótesis nula no puede ser rechazada. Esto sugiere que la varianza de tus datos de ventas sigue siendo igual al valor supuesto o incluso mayor.
Resumen
En esta guía hemos cubierto de manera exhaustiva cómo realizar una prueba F de dos muestras en Excel. Has aprendido cómo preparar tus datos, formular hipótesis, calcular el estadístico de prueba, determinar la región crítica y finalmente sacar conclusiones. Con estos pasos, estás bien preparado/a para realizar análisis estadísticos de forma autónoma.
Preguntas frecuentes
¿Qué es una prueba F de dos muestras?Una prueba F de dos muestras se utiliza para comparar las varianzas de dos grupos de datos.
¿Cómo formulo hipótesis para una prueba F?La hipótesis nula indica que la varianza es igual o mayor, mientras que la hipótesis alternativa asume una disminución.
¿Cómo encuentro el valor crítico para mi prueba?El valor crítico se puede derivar usando tablas de distribución de Chi-cuadrado, basándose en el nivel de confianza y los grados de libertad.
¿Qué hago si no puedo rechazar la hipótesis nula?Esto significa que los datos se ajustan al valor de varianza supuesto o incluso presentan mayores fluctuaciones.
¿Necesito software especial para la prueba?Excel es suficiente para realizar una prueba F de dos muestras, siempre y cuando los datos estén preparados.

