Los análisis de correlación de rangos son de vital importancia en la investigación estadística de relaciones entre variables. Especialmente cuando se trata de datos escalados de forma ordinal, la correlación de rangos de Spearman es un método valioso para identificar patrones y conexiones. En esta guía, aprenderás paso a paso cómo calcular la correlación de rangos de Spearman para una encuesta utilizando Excel.
Conocimientos clave
- La correlación de rangos mide la fuerza y dirección de una relación monótona entre dos variables ordinales.
- El coeficiente de correlación de rangos de Spearman es especialmente adecuado cuando una de las variables es ordinal y la otra está escalada de manera métrica.
- El cálculo en Excel puede realizarse utilizando fórmulas y funciones sencillas.
Guía paso a paso
En primer lugar, definimos las variables que deseamos analizar. En este caso, se trata de la satisfacción de los clientes (escala ordinal, valores del 1 al 3) y la cantidad de pedidos (escala métrica).
Para crear un orden de rangos para la satisfacción y la cantidad de pedidos, necesitarás una tabla que contenga los datos correspondientes. Asegúrate de introducir estos datos en Excel.

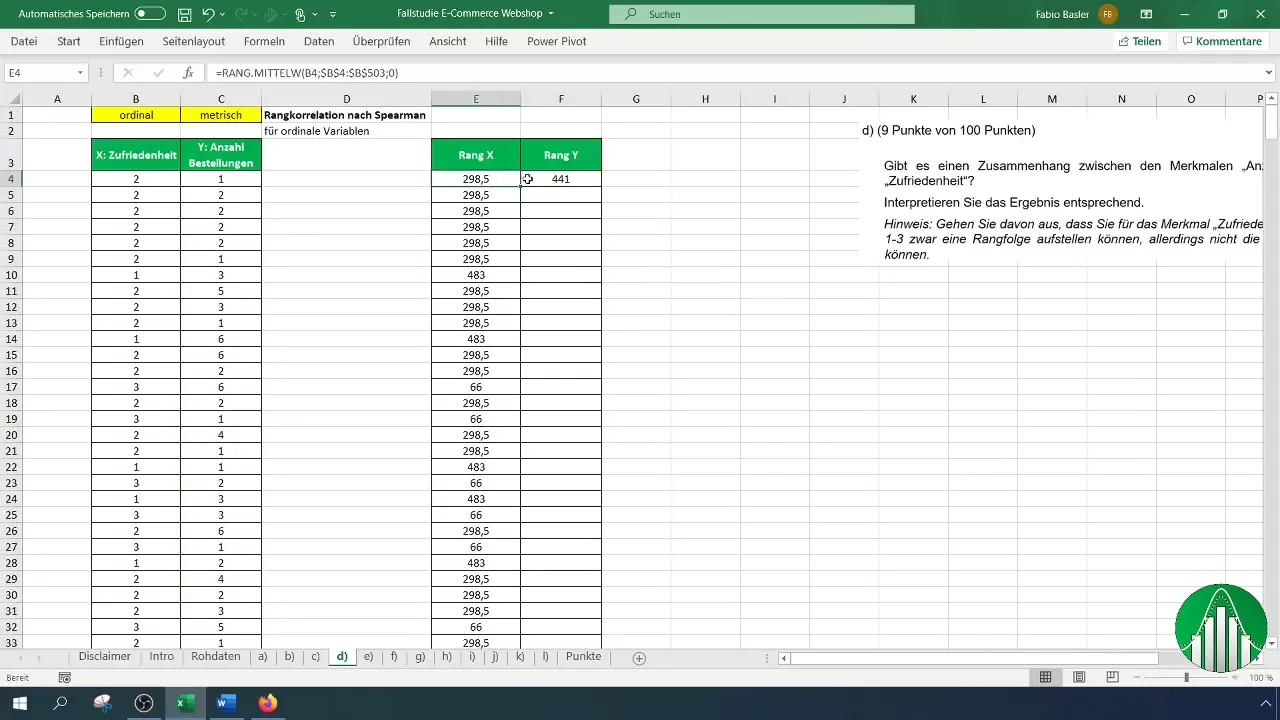
Una vez que hayas introducido tus datos en Excel, vamos a ver cómo calcular la correlación de rangos de Spearman. Para ello, utilizaremos la función "RANGO.MEDIO" en Excel, que devuelve el rango de un número dentro de una lista. Para la satisfacción, primero usaremos la siguiente fórmula:
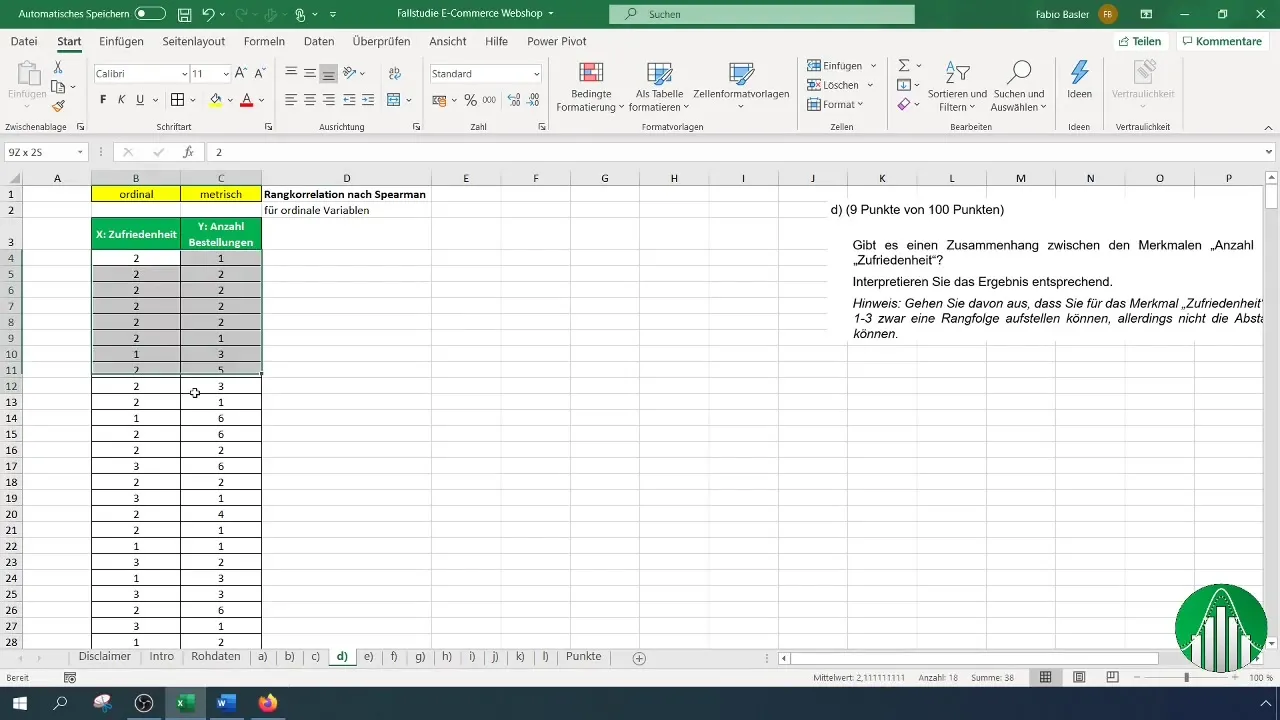
Al aplicar esta fórmula, debes asegurarte de seleccionar la columna de satisfacción y establecer el rango completo desde B4 hasta el final de tu serie de datos para identificar correctamente los rangos.
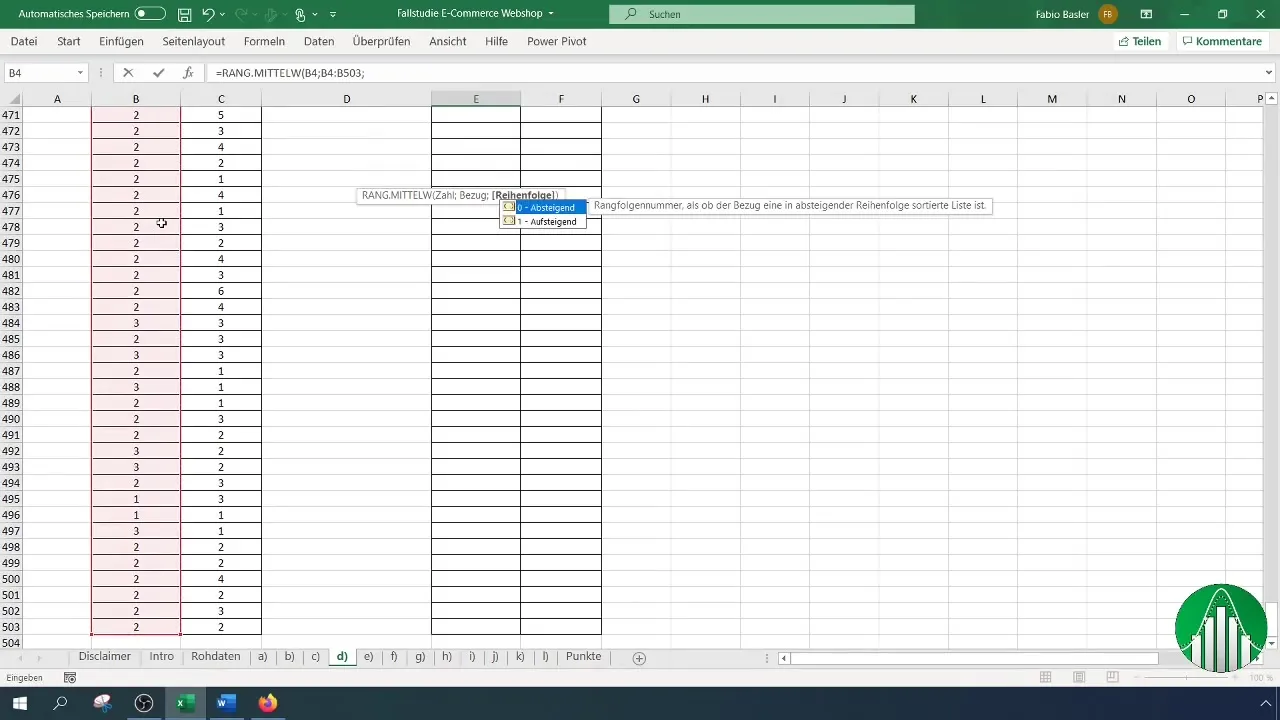
Decide si quieres ordenar los rangos de forma ascendente o descendente. Por lo general, es recomendable ordenarlos de forma ascendente. Destaca que las referencias de celda para los rangos deben estar fijas utilizando la tecla F4. Esto es importante para que las referencias no cambien al copiar.
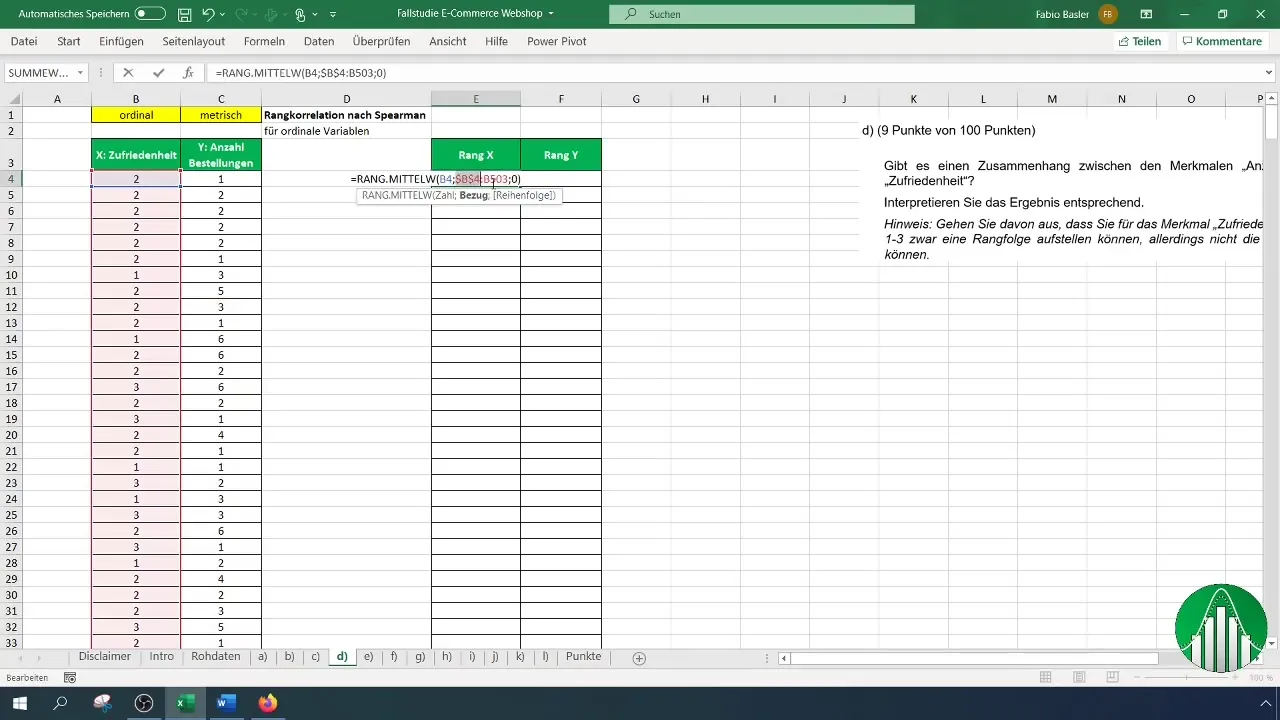
Una vez que hayas establecido los rangos para la satisfacción, repite el proceso para la cantidad de pedidos. Asegúrate de aplicar la fórmula y la referencia correctamente.
Con ambas listas de rangos (satisfacción y cantidad de pedidos) estás listo para calcular el coeficiente de correlación de rangos de Spearman. Para ello, utiliza la fórmula "=CORREL" para determinar la relación. La sintaxis es la siguiente:
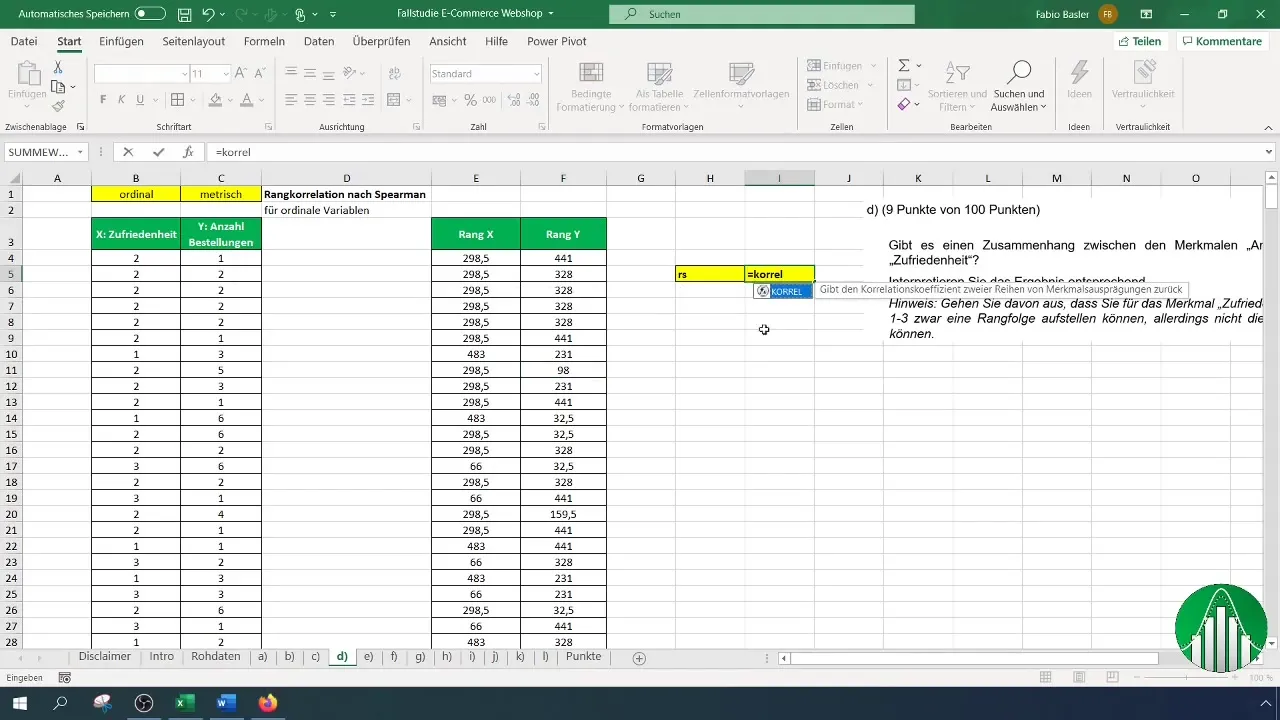
Indica la lista de rangos de satisfacción como primer argumento y la lista de rangos de pedidos como segundo. Excel calculará automáticamente el coeficiente de correlación de rangos de Spearman.

¿Cuál es el resultado de tu cálculo? Un valor del 5,61% indica una débil correlación positiva entre la satisfacción y la cantidad de pedidos. Esto significa que apenas existe una relación significativa entre estas dos variables.
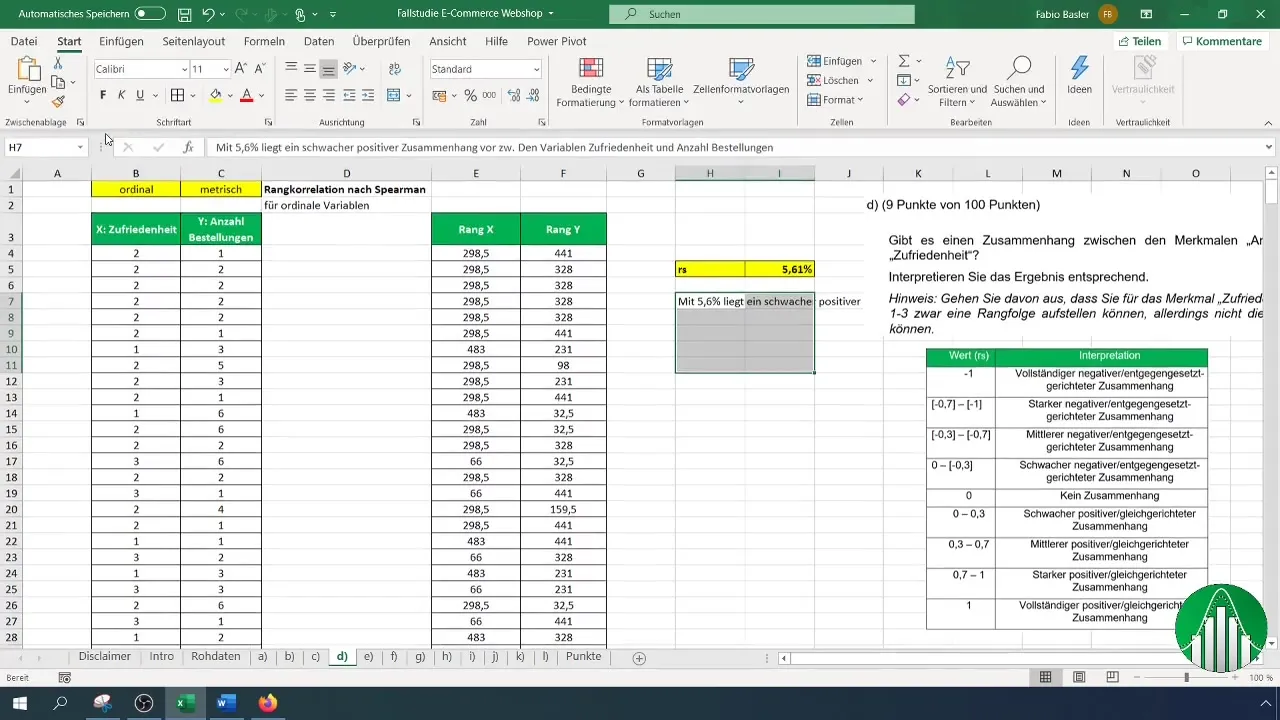
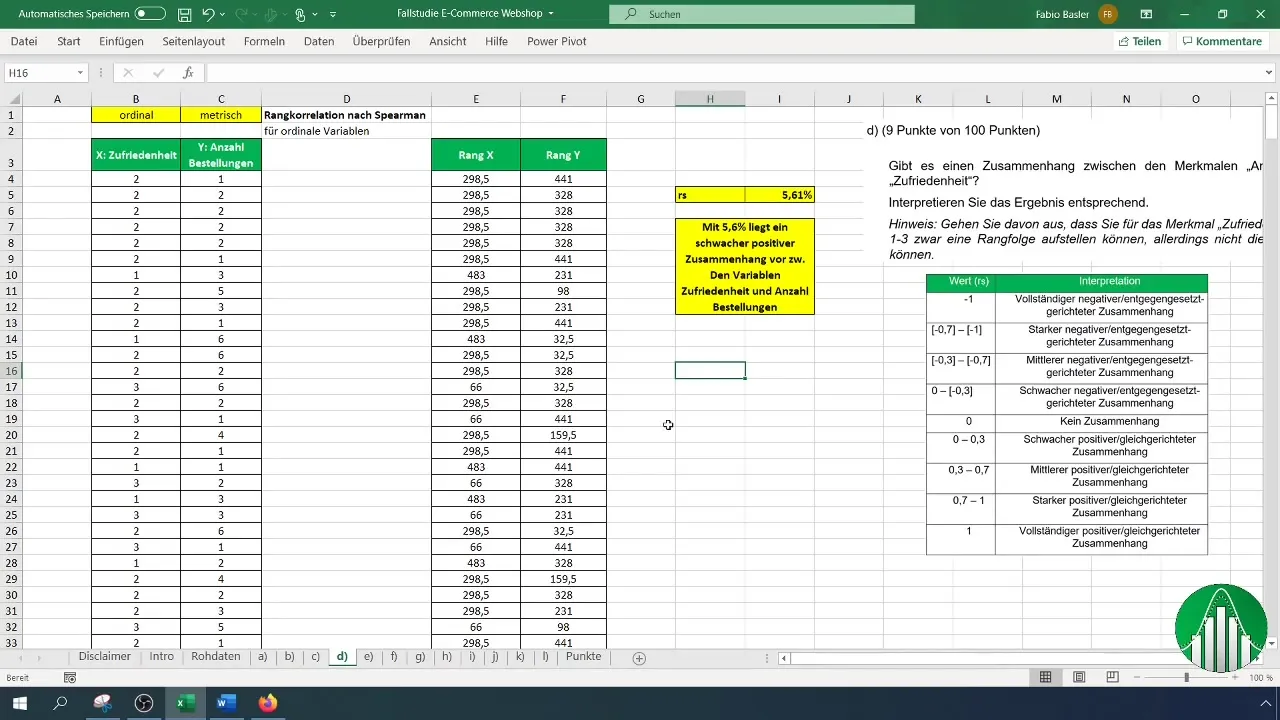
Para interpretar tus resultados, utiliza una tabla de valores que enumere las diferentes áreas de la correlación de rangos. Después de la interpretación, confirmamos que la baja tasa de correlación significa que las variables son relativamente independientes.
Resumen
Realizar un análisis de correlación de rangos de Spearman en Excel te permite obtener información valiosa sobre las relaciones entre variables ordinales y métricas. El método es sencillo de aplicar y ofrece una visión clara de posibles conexiones.
Preguntas frecuentes
¿Qué es el coeficiente de correlación de rangos de Spearman?El coeficiente de correlación de rangos de Spearman mide la fuerza y dirección de una relación monótona entre dos variables.
¿Cuándo tiene sentido usar el coeficiente de Spearman?Tiene sentido cuando al menos una de las variables está escalada ordinalmente.
¿Cómo calculo el coeficiente de Spearman en Excel?Usa la función "Rangos.Medios" para obtener los rangos, y luego la función "CORREL" para calcular la correlación.
¿Cuál es el rango de valores para el coeficiente de Spearman?El coeficiente está entre -1 y 1. Los valores cercanos a 1 indican una fuerte correlación positiva, mientras que los valores cercanos a -1 indican una fuerte correlación negativa.
¿Qué puede significar un valor de 5,61% en la correlación de rangos?Un valor de 5,61% indica una débil correlación positiva, lo que sugiere que las variables son relativamente independientes entre sí.


