La distribución normal es un concepto central en la teoría de la probabilidad y estadística. En cada conjunto de datos que está distribuido de manera uniforme, observamos la llamada curva de campana, que a menudo se encuentra en encuestas y análisis de ventas. En este tutorial aprenderás cómo calcular y visualizar la distribución normal para una encuesta utilizando Excel, para determinar probabilidades clave. Con estas habilidades, no solo podrás comprender mejor tus datos, sino que también podrás utilizarlos de manera efectiva para tomar decisiones fundamentadas.
Principales conclusiones
- Aprenderás el cálculo paso a paso de la distribución normal en Excel.
- Se mostrarán las posibilidades de representación gráfica de una distribución normal.
- Comprenderás cómo calcular probabilidades para eventos específicos.
Guía paso a paso
Primero, asegúrate de que todos los datos necesarios estén disponibles en una tabla de Excel. Estos datos representan, por ejemplo, las ventas de una encuesta.
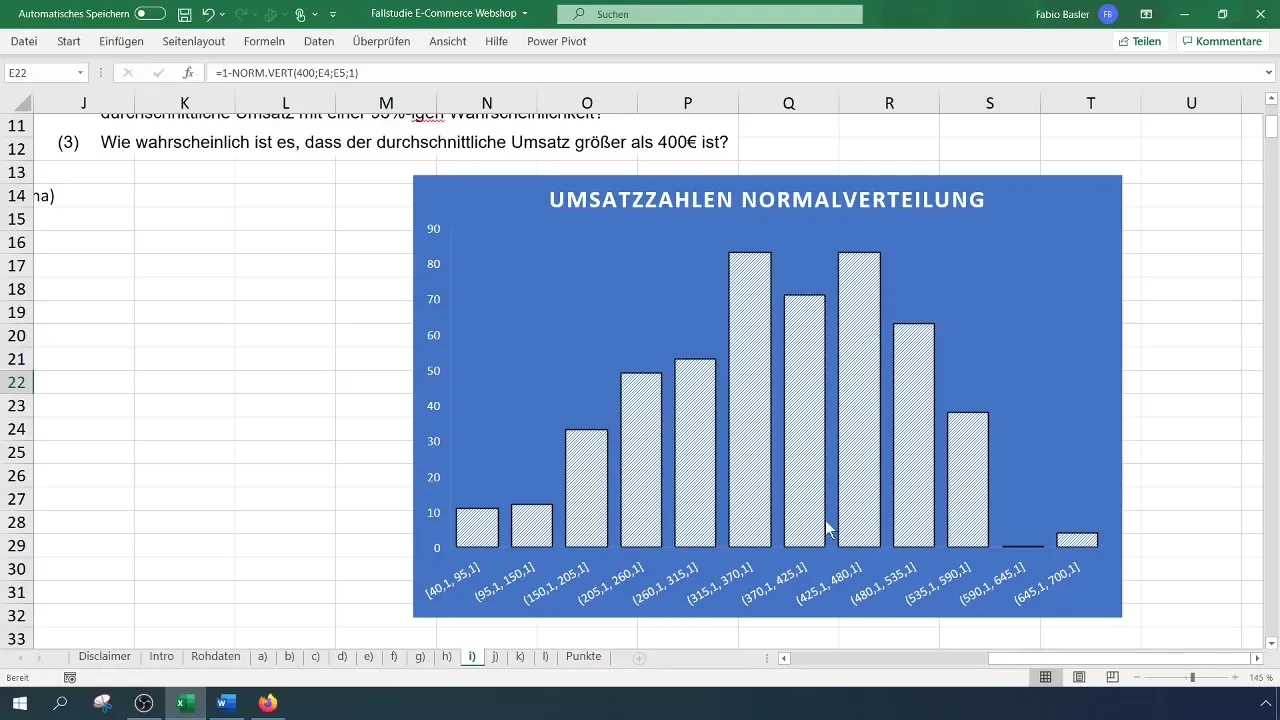
Visualización de la distribución normal
Para representar gráficamente la distribución normal de las ventas, sigue estos pasos:
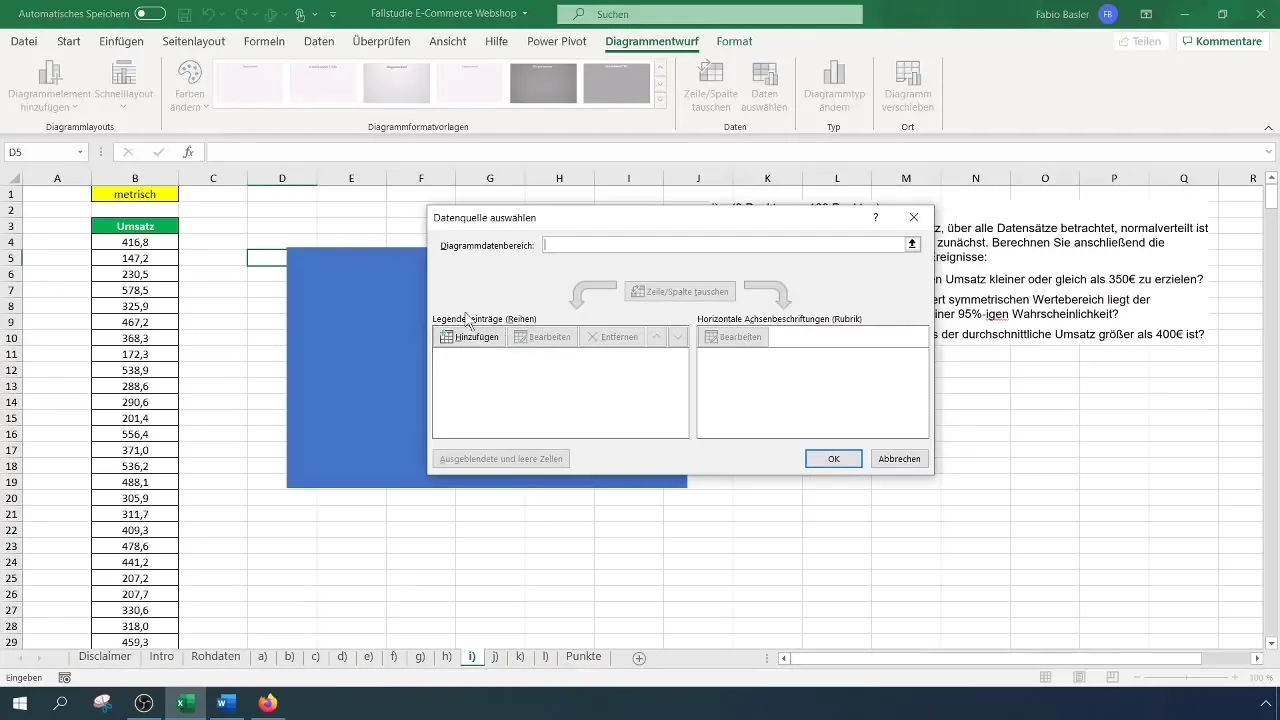
Primero, selecciona los datos de ventas en tu tabla de Excel y cópialos en una nueva columna. En la barra de menú, haz clic en "Insertar" y selecciona "Gráfico". Aquí elige un histograma para representar visualmente la distribución. Puedes seleccionar un histograma vacío para mostrar los valores estándar de tus datos.

Haz clic derecho en el gráfico y selecciona "Seleccionar datos". En la ventana que se abre, agrega tus datos de ventas como la primera serie de datos. En los valores de fila, selecciona todos los conjuntos de datos manteniendo presionada la tecla Shift y seleccionando los valores.
Una vez que los datos se muestren en el histograma, puedes personalizar el título del gráfico para que sea más representativo. Por ejemplo, cambia el título a "Distribución normal de ventas". Asegúrate de que la curva de campana sea reconocible; esto indica una distribución normal.
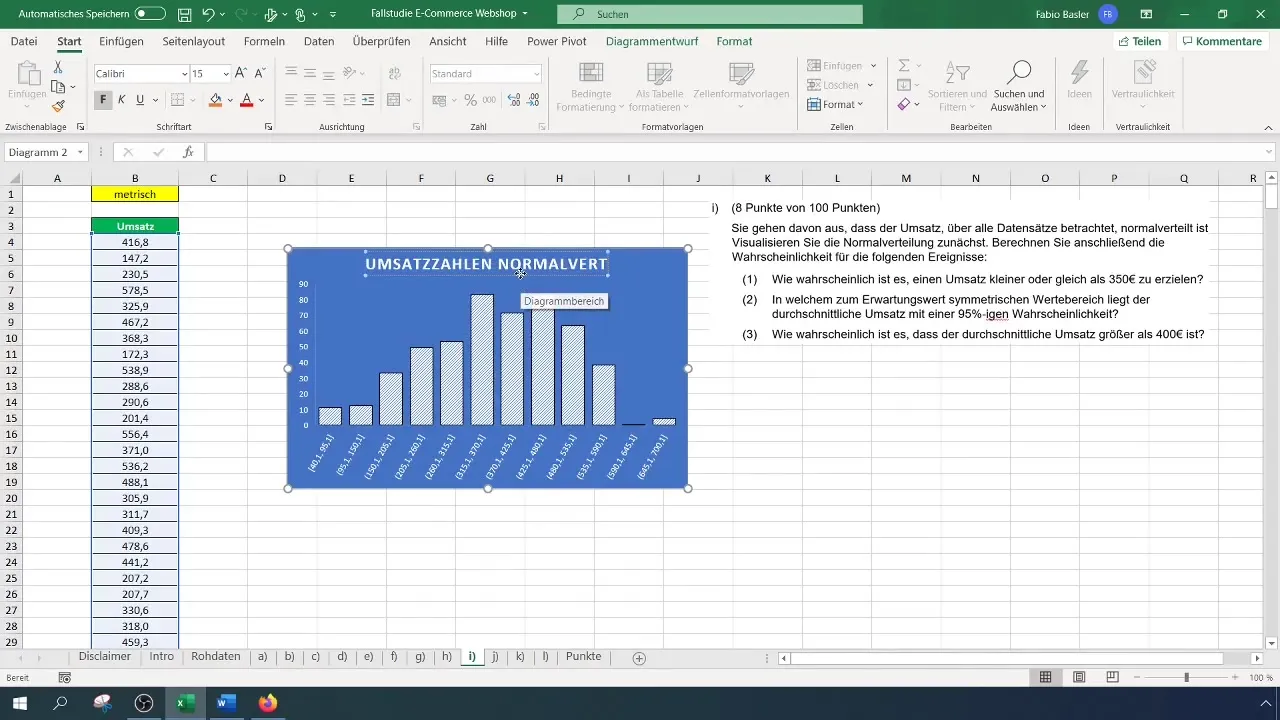
Cálculo de probabilidades
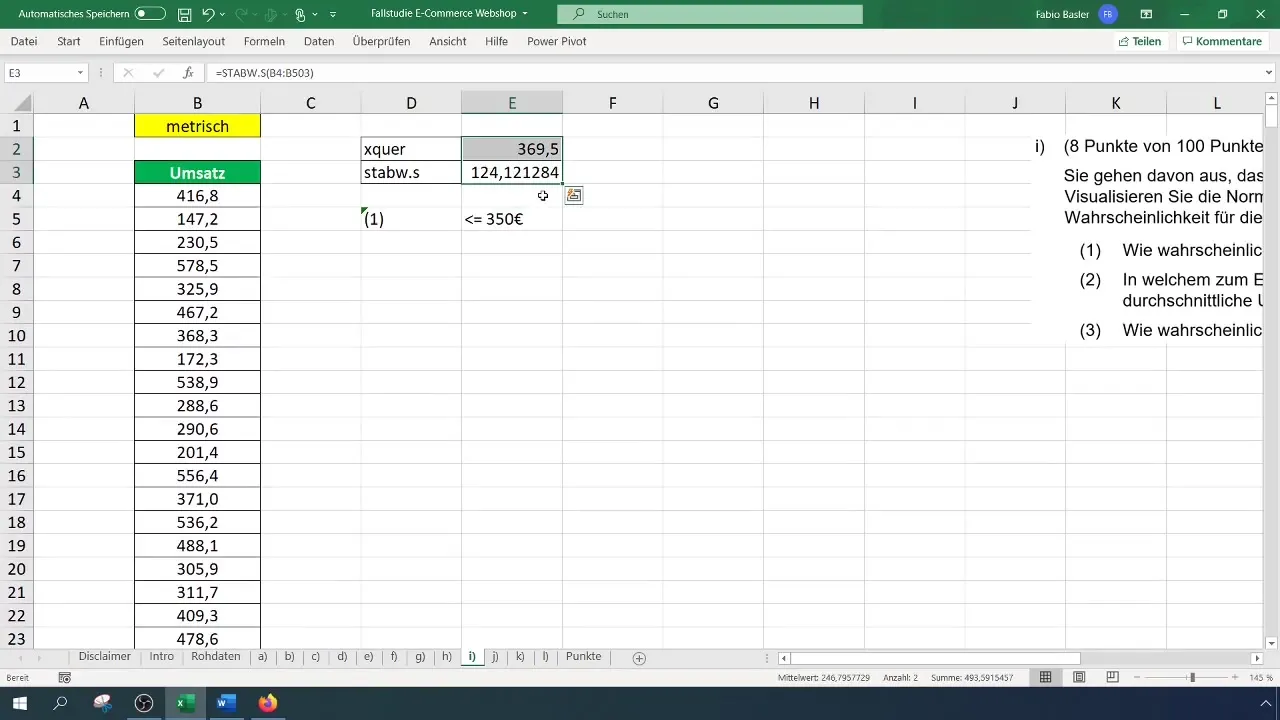
La siguiente tarea consiste en determinar la probabilidad de que las ventas sean menores o iguales a 350 euros. Para esto, necesitarás la media y la desviación estándar de los datos de ventas.
Para calcular la media, utiliza la fórmula =PROMEDIO(A1:A100) (Aquí reemplaza A1:A100 con el rango de datos real). En tu ejemplo, esto podría resultar en una venta promedio de 369 euros.
Para la desviación estándar, utiliza la fórmula =DESVESTP(A1:A100), lo que podría resultar en aproximadamente 124,12 euros en tu caso.
Ahora puedes calcular la probabilidad de tener una venta de 350 euros. Esto se hace utilizando la fórmula: =DISTR.NORM(350; Media; Desviación_estándar; VERDADERO). Inserta los valores correspondientes y presiona Enter.
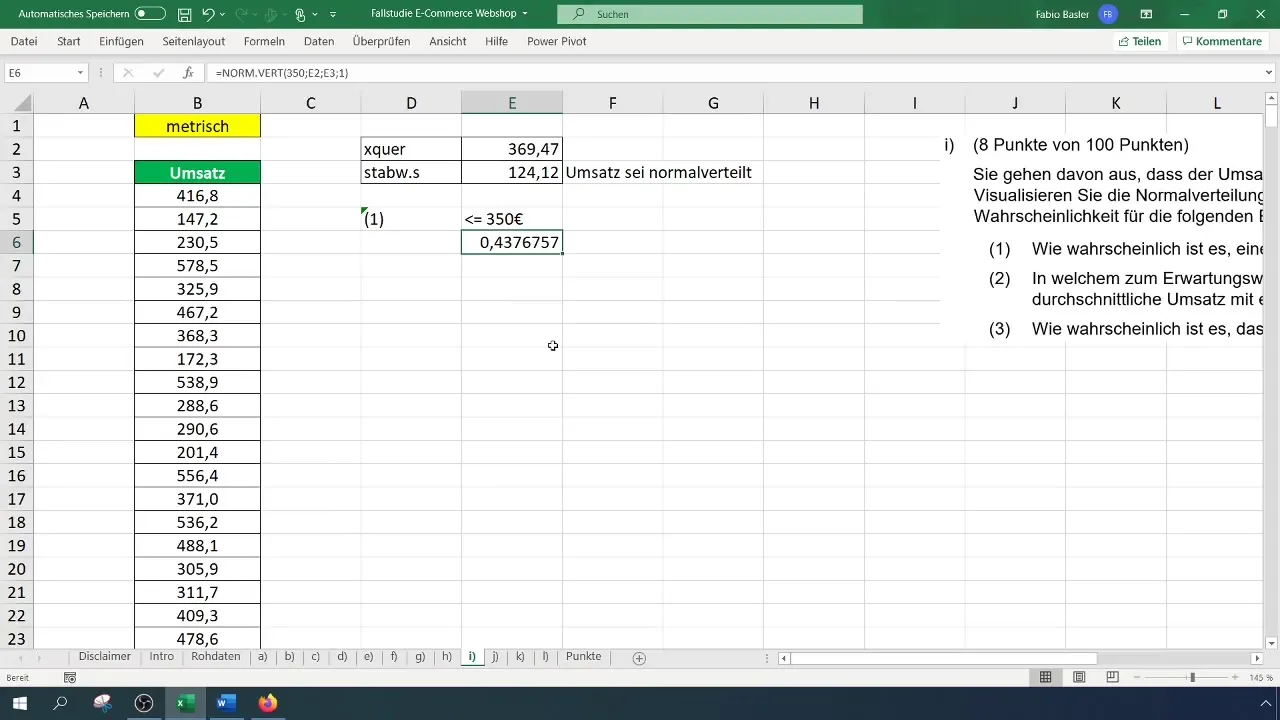
El resultado de este cálculo podría indicarte que la probabilidad de tener una venta menor o igual a 350 euros es de aproximadamente 43,8 %. Para ilustrarlo, puedes formatear los valores y cambiarlos a representación porcentual.
Cálculo del rango de valores simétrico al valor esperado
El próximo objetivo es determinar el rango de valores simétrico al valor esperado con una probabilidad del 95 %. Para esto, debes encontrar el valor cuantitativo para el 95 %.
Esto se logra ingresando la fórmula =INV.NORM.S(0,95) en una celda, lo que te dará un valor de percentil de 1,65.
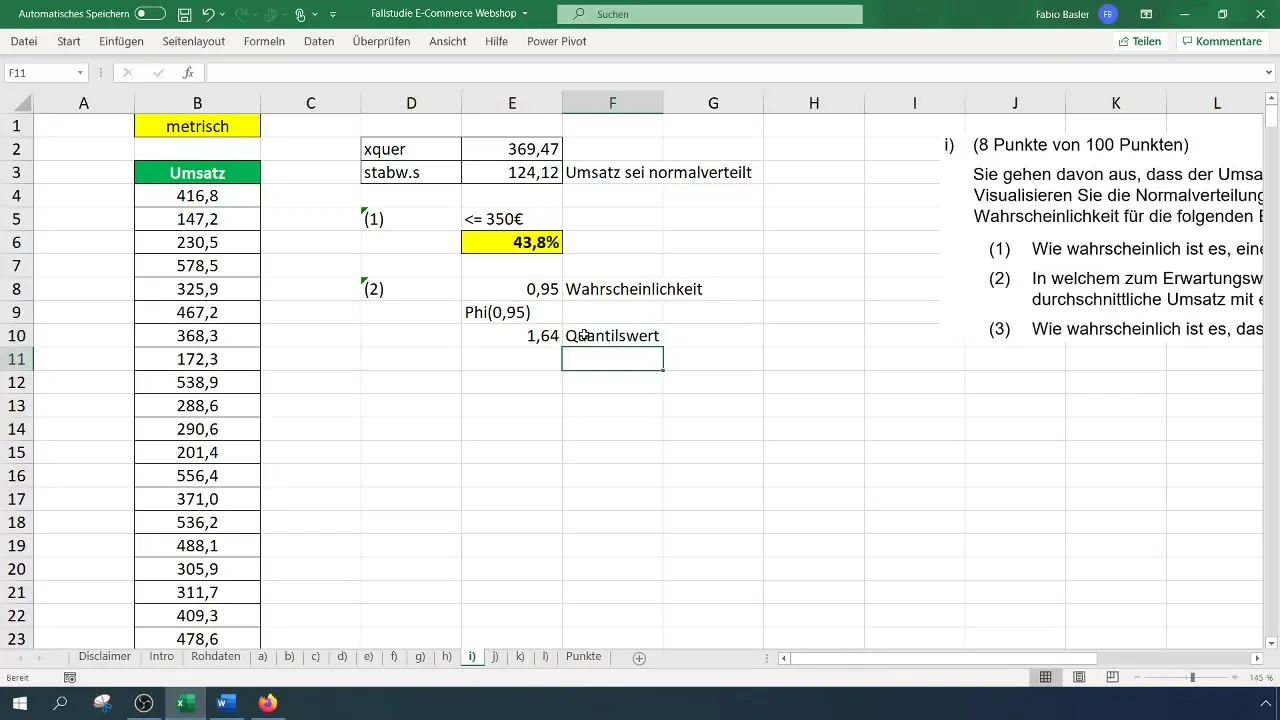
Luego, inserta este cálculo en una ecuación para encontrar el rango de valores. La fórmula podría verse así: Valor_esperado + (Desviación_estándar * valor_de_percentil). Inserta los valores correspondientes y calcula el rango de valores simétrico.
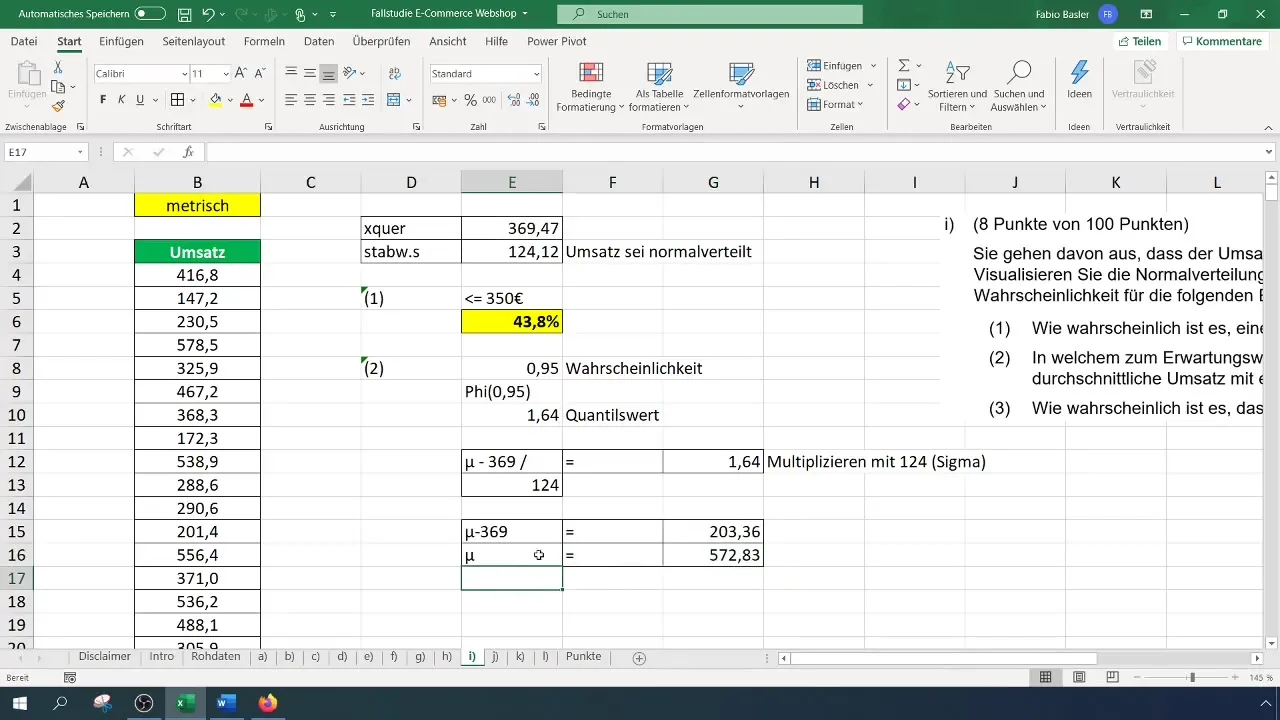
Si, por ejemplo, obtienes un valor de 572 euros, eso significa que puedes esperar una facturación dentro de este rango con una probabilidad del 95 %.
Probabilidades de facturaciones más altas
Para el último cálculo, determinarás la probabilidad de que la facturación sea mayor a 400 euros. Para esto, debes utilizar la fórmula =1 - NORM.DIST(400; Media; Desviación estándar; VERDADERO).
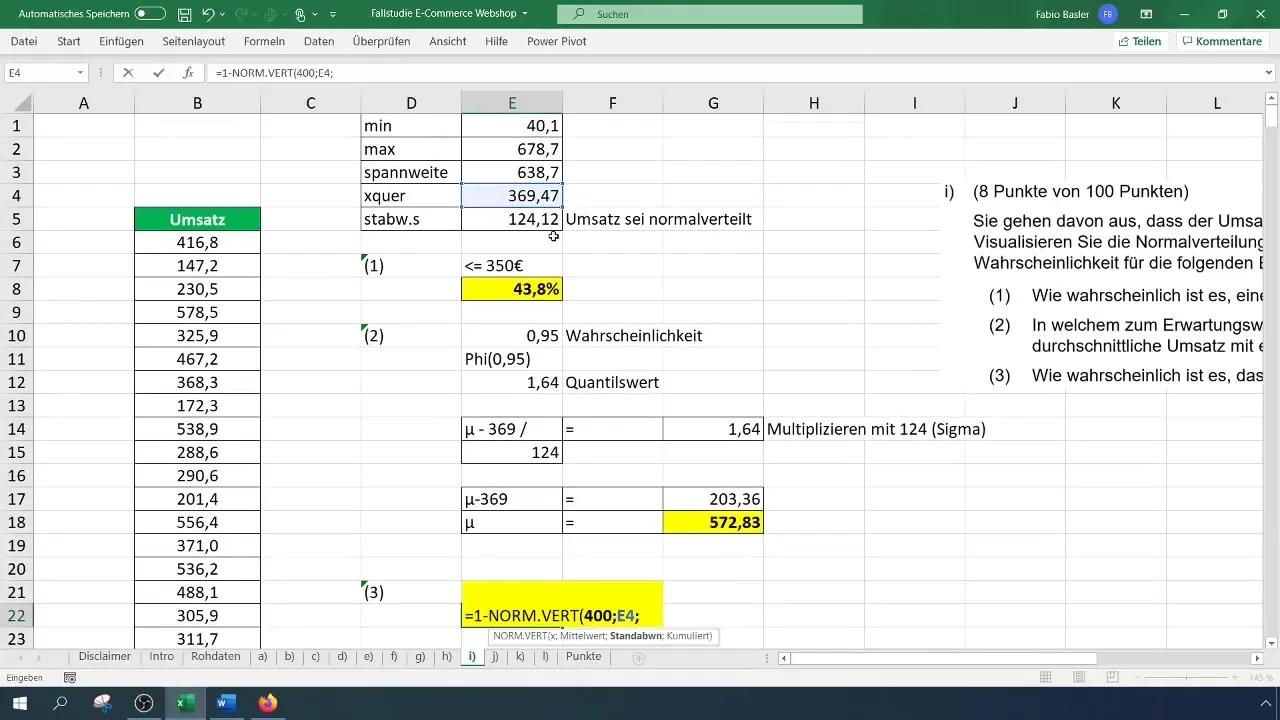
La probabilidad podría ser del 40 % en este caso también. Estos valores son importantes de cuestionar. Al observar la escala en el histograma, se puede rastrear la consistencia del porcentaje de facturaciones más altas.
Resumen
En este tutorial aprendiste cómo utilizar la distribución normal en Excel para el cálculo de probabilidades. Basado en ejemplos prácticos de una encuesta, has aprendido cómo manejar datos tanto gráficamente como matemáticamente. Comprender estos conceptos te ayudará a implementar análisis estadísticos de manera exitosa en tus proyectos.
Preguntas frecuentes
¿Cómo calculo la desviación estándar en Excel?Utiliza la fórmula =DESVIACION.ESTANDAR(RangoDatos) para calcular la desviación estándar.
¿Puedo usar la distribución normal para datos no normales?La distribución normal es más adecuada para datos distribuidos de manera normal. De lo contrario, los resultados podrían ser engañosos.
¿Cómo puedo personalizar los gráficos en Excel?Haz clic en los gráficos y selecciona las opciones de formatos en la barra de menú para diseñar el gráfico según tus necesidades.


