El cálculo de los intervalos de confianza es una parte esencial del análisis estadístico, especialmente cuando se trata de inferir conclusiones sobre una población a partir de una muestra. En esta guía te mostraré cómo calcular un intervalo de confianza de dos lados para el promedio de ventas de una encuesta en Excel . Aprenderás qué pasos diferentes son necesarios para llegar desde los datos brutos hasta el intervalo de confianza final y cómo implementar esta metodología en Excel.
Principales conclusiones:
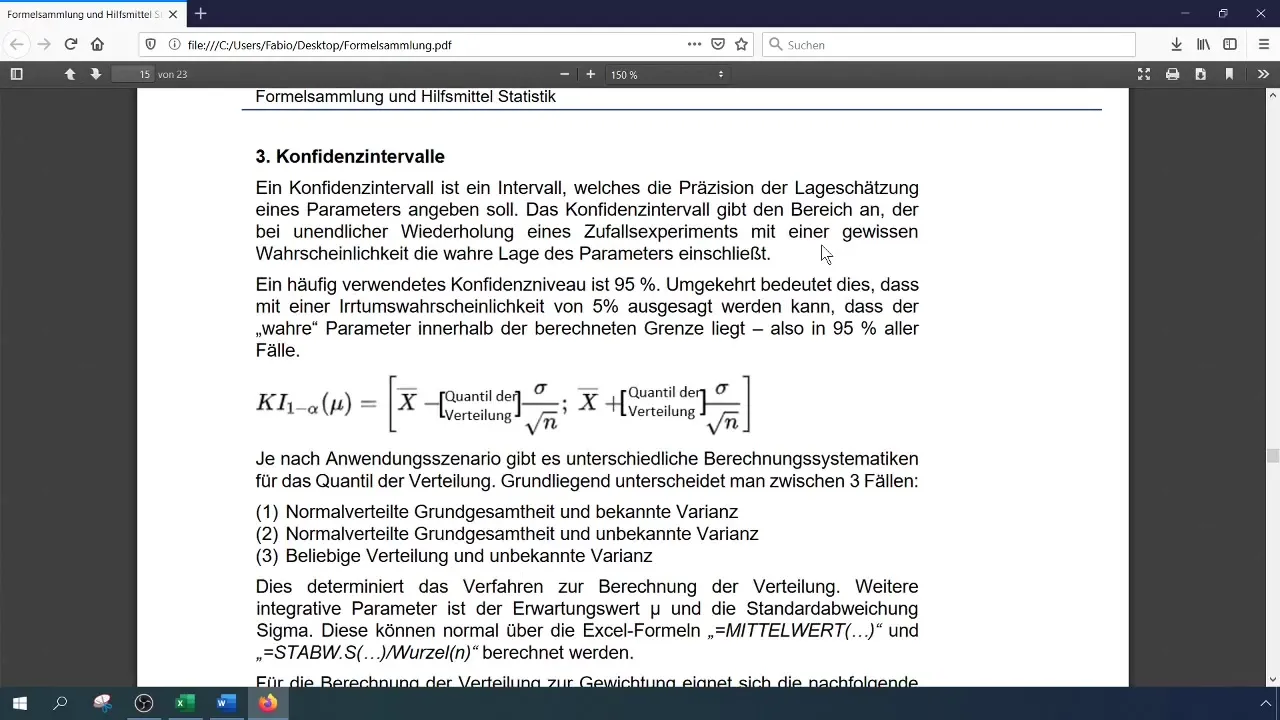
- Un intervalo de confianza de dos lados indica dentro de qué límites puede estar la verdadera media de ventas con cierta probabilidad de confianza.
- Para el cálculo necesitas la media, la desviación estándar, el tamaño de la muestra y el cuantil t correspondiente.
- Excel te proporciona las funciones necesarias para calcular estos valores y representar visualmente el intervalo de confianza.
Instrucciones paso a paso
Paso 1: Preparar los datos.
En primer lugar, debes preparar los datos relevantes en Excel. Para el ejemplo, consideraremos únicamente a los clientes normales, ya que se quiere calcular la media de ventas solo para este grupo.

Puedes seleccionar y copiar los datos en tu hoja de cálculo para pegarlos en una nueva área. Esto te ayudará a filtrar tu análisis para los grupos de clientes correspondientes.
Paso 2: Recopilar información básica.
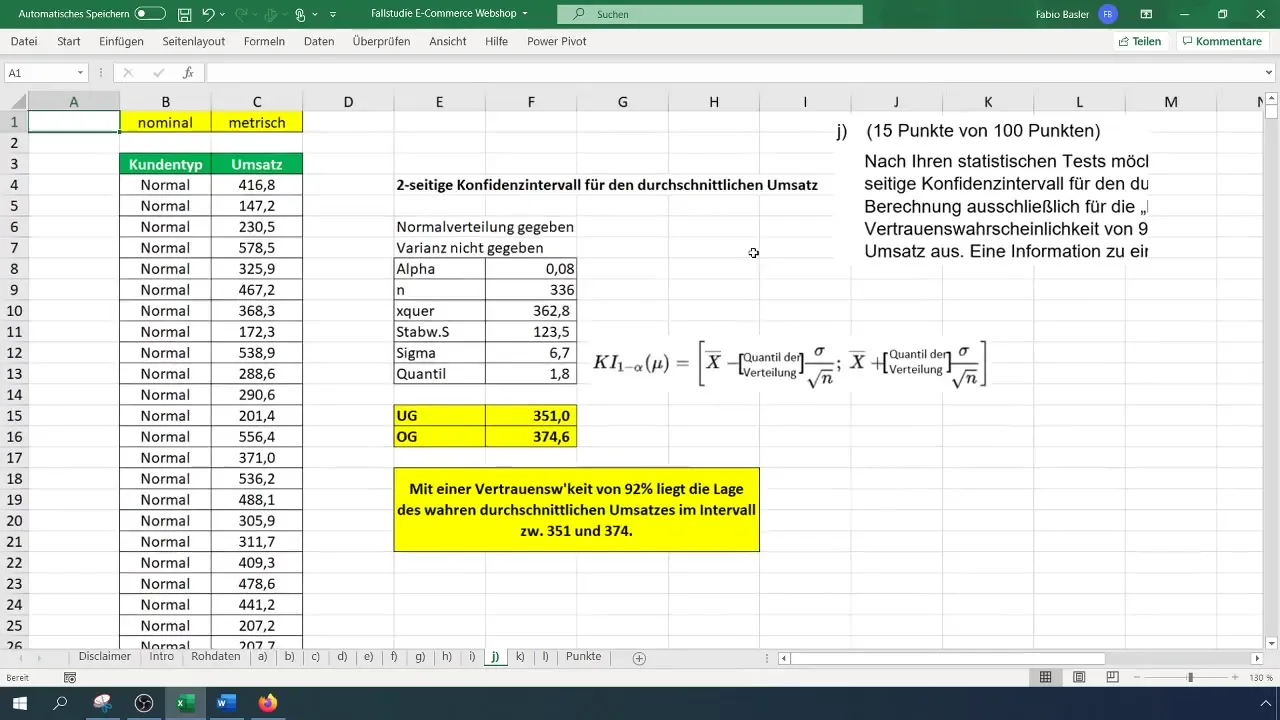
Crea una tabla simple en Excel donde registres todos los parámetros importantes. Estos son el tamaño de la muestra (n), la media (x̄), la desviación estándar (σ) y el cuantil relevante. Ya sabemos que asumiremos una distribución normal y que no tenemos varianza disponible.

Paso 3: Calcular el tamaño de la muestra (n).
Para determinar el número de observaciones de los clientes normales, debes recortar los datos relevantes y encontrar el número con la FÓRMULA =NÚMERO(). En este caso, deberías obtener 336 observaciones de los datos filtrados.
Paso 4: Calcular la media (x̄).
Calcula la media de las ventas aplicando la fórmula =PROMEDIO(). Esto te dará la media de ventas para los clientes normales, que en nuestro ejemplo es de 362,80 euros.
Paso 5: Determinar la desviación estándar (σ).
Aplica la fórmula =DESVEST.S() para calcular la desviación estándar. Esta se necesita para la estadística inductiva, por lo que usamos la desviación estándar para la muestra. El valor calculado es de 123 euros.
Paso 6: Calcular Sigma (σ / √n).
Ahora calcula la desviación estándar para la media, dividiendo la desviación estándar por la raíz cuadrada del tamaño de la muestra. Utiliza la fórmula: =Desviación estándar/RAÍZ(Tamaño de la muestra).
Paso 7: Encontrar el cuantil t.
Dado que tenemos una distribución normal con una varianza desconocida, debemos encontrar el cuantil t. Utiliza la función de Excel =T.INV.2T() especificando el nivel de alfa (0,08) y los grados de libertad (n-1). En tu caso, esto da como resultado un valor t de 1,8.
Paso 8: Calcular el límite inferior del intervalo de confianza.
Ahora calcula el límite inferior del intervalo de confianza. La fórmula es: =Media - (valor t * Sigma). Esto te dará el límite inferior, que en nuestro ejemplo es de 351 euros.
Paso 9: Calcular el límite superior del intervalo de confianza.
Ahora puedes calcular el límite superior del intervalo de confianza. La fórmula es similar, pero esta vez sumas el valor t a tu media: =Media + (valor t * Sigma). Esto te dará un límite superior de 374 euros.
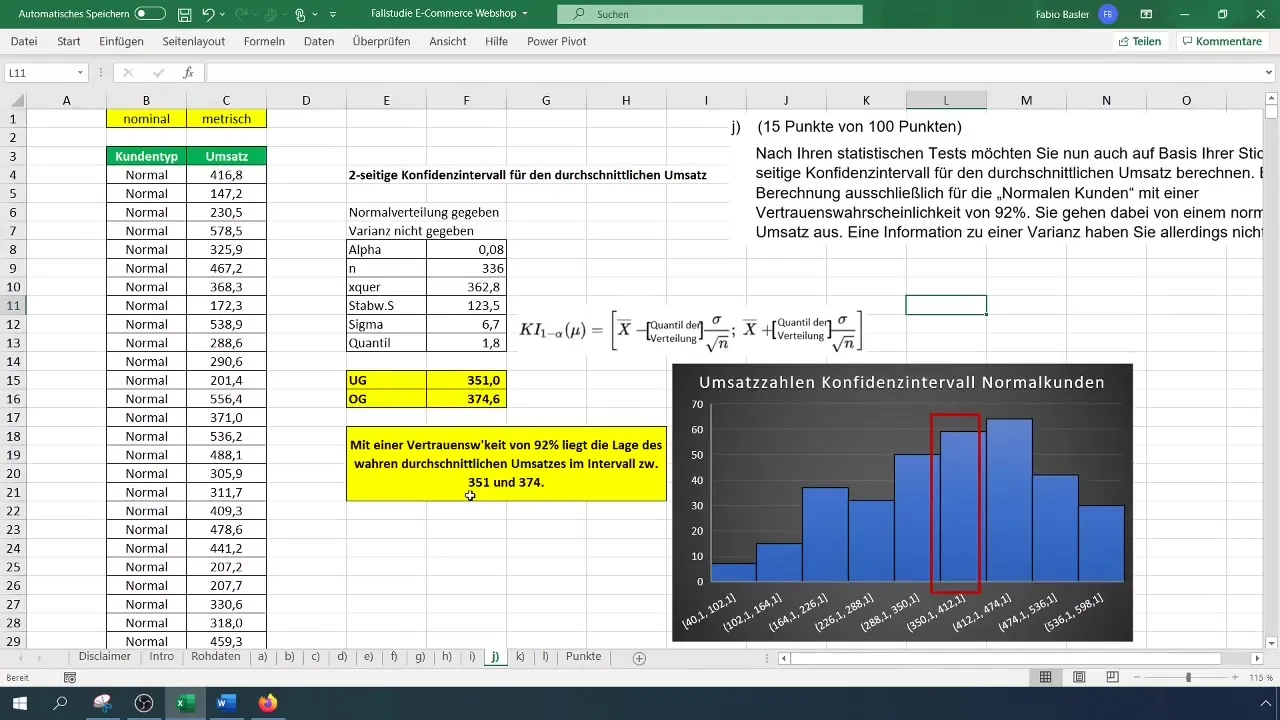
Paso 10: Representación del intervalo de confianza.
Para visualizar tus resultados, puedes crear un histograma en Excel y marcar en él el intervalo de confianza. Dibuja una línea entre el límite inferior y superior para mostrar en qué rango se encuentra la verdadera media de ventas de los clientes normales con una probabilidad de confianza del 92%.
Paso 11: Interpretación y Conclusión
Ahora puedes afirmar que con una probabilidad de confianza del 92%, el verdadero promedio de ventas de los clientes normales se encuentra entre 351 y 374 euros. Esto es importante para tomar decisiones adicionales en tu empresa.
Resumen
En este tutorial has aprendido cómo calcular un intervalo de confianza bidireccional para el promedio de ventas en Excel. Has seguido todos los pasos necesarios, desde la preparación de datos hasta la representación gráfica e interpretación de los resultados.


