Los cálculos estadísticos son una parte indispensable del análisis de datos, especialmente en un entorno de comercio electrónico. El análisis de datos históricos permite determinar probabilidades que son cruciales para las empresas. En esta guía aprenderás cómo calcular probabilidades utilizando la distribución de Poisson en Excel, basándote en un ejemplo de encuesta.
Principales conclusiones La distribución de Poisson permite determinar la probabilidad de eventos que ocurren en un marco temporal fijo. En este ejemplo, calcularás la probabilidad de que más de dos, pero como máximo cuatro clientes compren algo en una tienda de comercio electrónico en una hora, así como la probabilidad de que más de dos clientes compren algo en total.
Guía paso a paso
Comencemos con el cálculo de las probabilidades para los eventos descritos.
Paso 1: Comprender los fundamentos de la distribución de Poisson
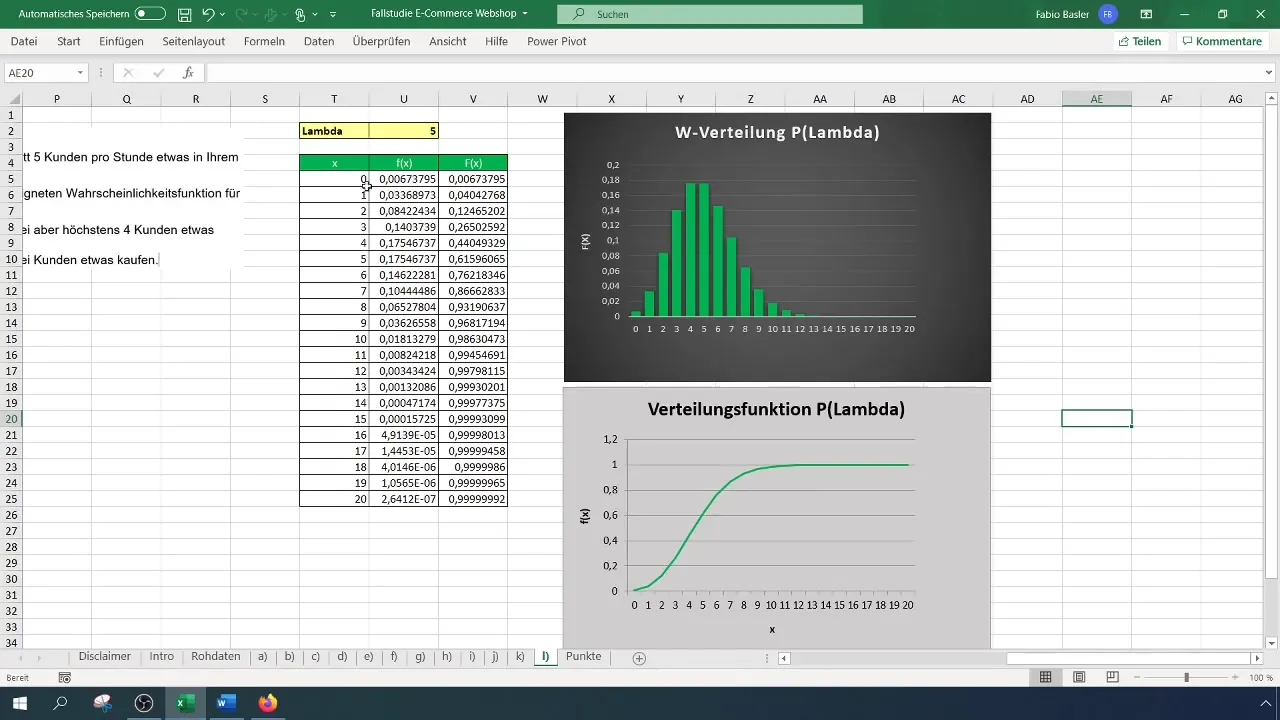
Lo primero que debes hacer es entender qué es la distribución de Poisson. Esta distribución discreta de probabilidades se utiliza para cuantificar la cantidad de eventos en períodos de tiempo fijos. En el ejemplo actual, tenemos una media de cinco compras por hora. Esto se formula como valor Lambda (λ = 5).

Paso 2: Preparar los datos en Excel
Abre Excel y prepara una nueva tabla. Asegúrate de tener visibles los parámetros relevantes (Lambda y la cantidad de eventos deseados).
Paso 3: Determinar probabilidades de compras por clientes
Para el primer escenario, quieres calcular la probabilidad de que más de dos y como máximo cuatro clientes compren algo. Para ello, debes calcular las probabilidades para dos y cuatro clientes y luego determinar la diferencia entre ellas.

Paso 4: Utilizar la fórmula de Excel para la distribución de Poisson
Utiliza la función POISSON.DIST para calcular las probabilidades. La fórmula es la siguiente:
- Para dos compradores: =POISSON.DIST(2; 5; VERDADERO).
- Para cuatro compradores: =POISSON.DIST(4; 5; VERDADERO).
Paso 5: Interpretar los resultados
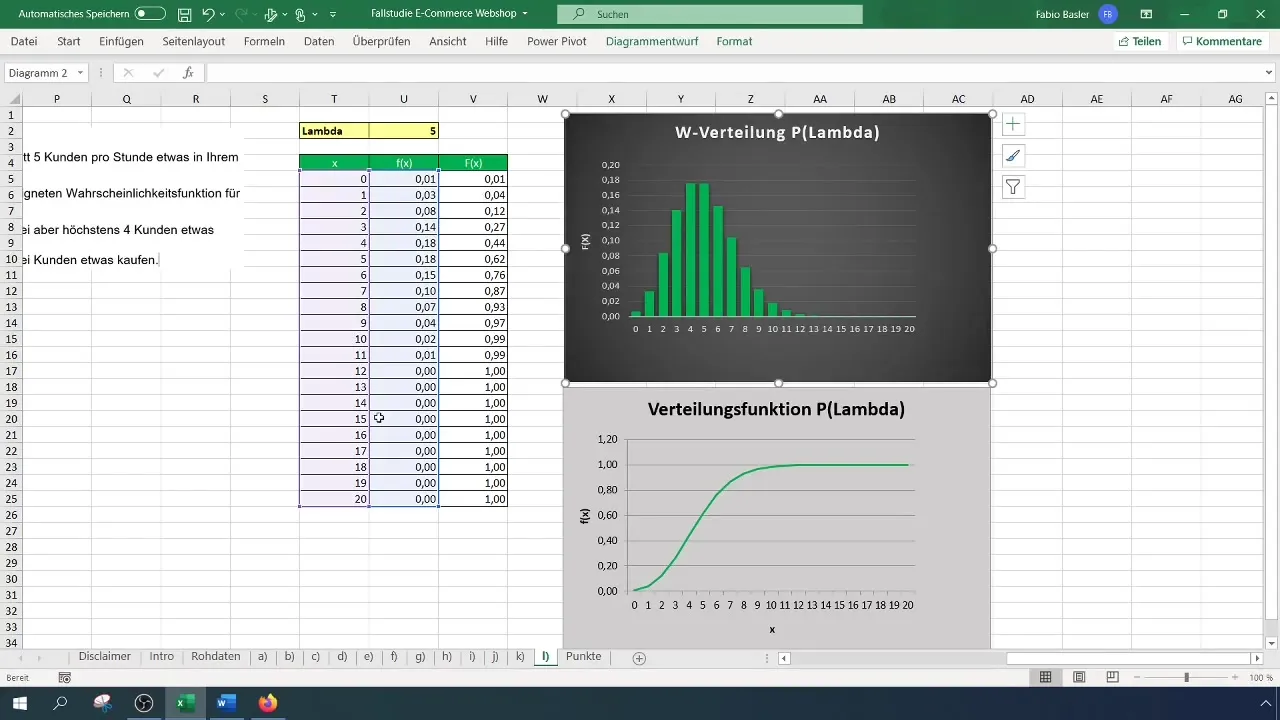
Después de aplicar las fórmulas, obtendrás dos probabilidades, por ejemplo, 12% para dos clientes y 44% para cuatro clientes. Luego restas la probabilidad de dos compradores de la de cuatro compradores, lo que te dará una probabilidad del 32% de que más de dos pero como máximo cuatro clientes compren algo.
Paso 6: Calcular más probabilidades
Ahora se trata de calcular la probabilidad de que más de dos clientes compren en tu tienda de comercio electrónico. Para ello, primero calculas la probabilidad de exactamente dos compradores y luego restas este resultado de 1.
Paso 7: Utilizar la fórmula de Excel para más de dos compradores
La fórmula de Excel es: =1 - POISSON.DIST(2; 5; VERDADERO). Esto te dará la probabilidad de que más de dos clientes compren, que en este caso es del 88%.
Paso 8: Resumen de los resultados
Después de realizar todos los cálculos, anota las probabilidades clave. Has descubierto que la probabilidad de que más de dos pero como máximo cuatro clientes realicen pedidos es del 32%, mientras que la probabilidad de que más de dos clientes compren en total es del 88%.
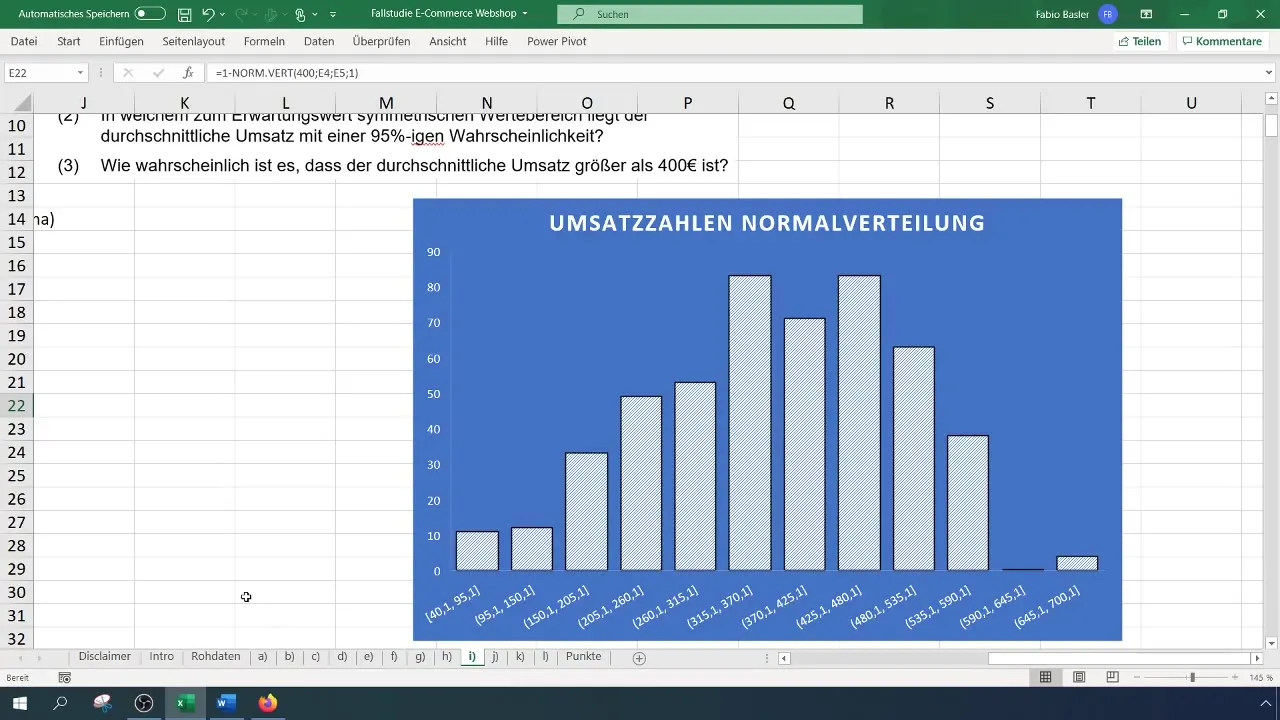
Resumen
En esta guía has aprendido a utilizar la distribución de Poisson para calcular probabilidades en Excel. Has seguido pasos para calcular y interpretar probabilidades para eventos específicos.
FAQ frecuentes
¿Qué es la distribución de Poisson?La distribución de Poisson es una distribución discreta de probabilidades que indica cuántas veces ocurre un evento en un período de tiempo fijo.
¿Cómo calcular probabilidades con la distribución de Poisson en Excel?Utilizas la función POISSON.DIST para calcular probabilidades para diferentes valores.
¿Qué significa un valor Lambda de 5?Un valor Lambda de 5 significa que, en promedio, ocurren cinco eventos (por ej., compras) en el intervalo de tiempo definido (por ej., una hora).
¿Qué valores debo proporcionar para la distribución de Poisson?Debes indicar la cantidad de eventos deseados (x), la media (λ) y si deseas calcular probabilidades acumuladas.
¿Por qué es importante la distribución de Poisson para el comercio electrónico?La distribución de Poisson ayuda a analizar patrones de compra y predecir la probabilidad de actividades de los clientes, lo que puede apoyar decisiones importantes en marketing y gestión de inventario.


