Statistika on oluline tööriist analüüsideks mitmes valdkonnas. See juhend näitab sulle, kuidas teha Spearmani reitingukorreleeriv analüüs Excelis . Selle meetodiga saad efektiivselt mõõta järjestusmuutujate vahelist seost. Vaatleme kliendirahulolu ja turundustaseme suhet.
Peamised järeldused
- Spearmani reitingukorreleeriv analüüs sobib eriti hästi järjestuskaalutud andmete puhul.
- Exceli kasutamine võimaldab rahuldavalt arvutada ja visualiseerida reitingukorrelatsiooni.
- Nõrk positiivne seos turundustasemete ja kliendirahulolu vahel näitab, et rohkem investeerimine turundusse ei pruugi tingimata viia suurema rahuloluni.
Juhis samm-sammult
Esmalt ei saa sa vältida oluliste andmete sisestamist. Keskkendume kliendirahulolule ja turundustasemetele. Need andmed koguti juhtumiuuringu raames.
Sel juhul saad kõigepealt kopeerida andmed oma algandmestikust ja kleepida need uude töölehele. Jälgi, et veergude pealkirjad oleksid selgelt määratletud. Oleks abiks nimetada veerge "Kliendirahulolu" ja "Turundustase".
Pärast andmete kopeerimist on oluline kontrollida oma muutujate skaalatasemeid. Klientide rahulolu on järjestikune, samas kui turundustasemed on samuti järjestikused kategooriad. Kontrolli kindlasti, et saad aru, kas see on õigesti mõistetud, et hilisemaid arvutusi vigade vältimiseks õigesti teha.
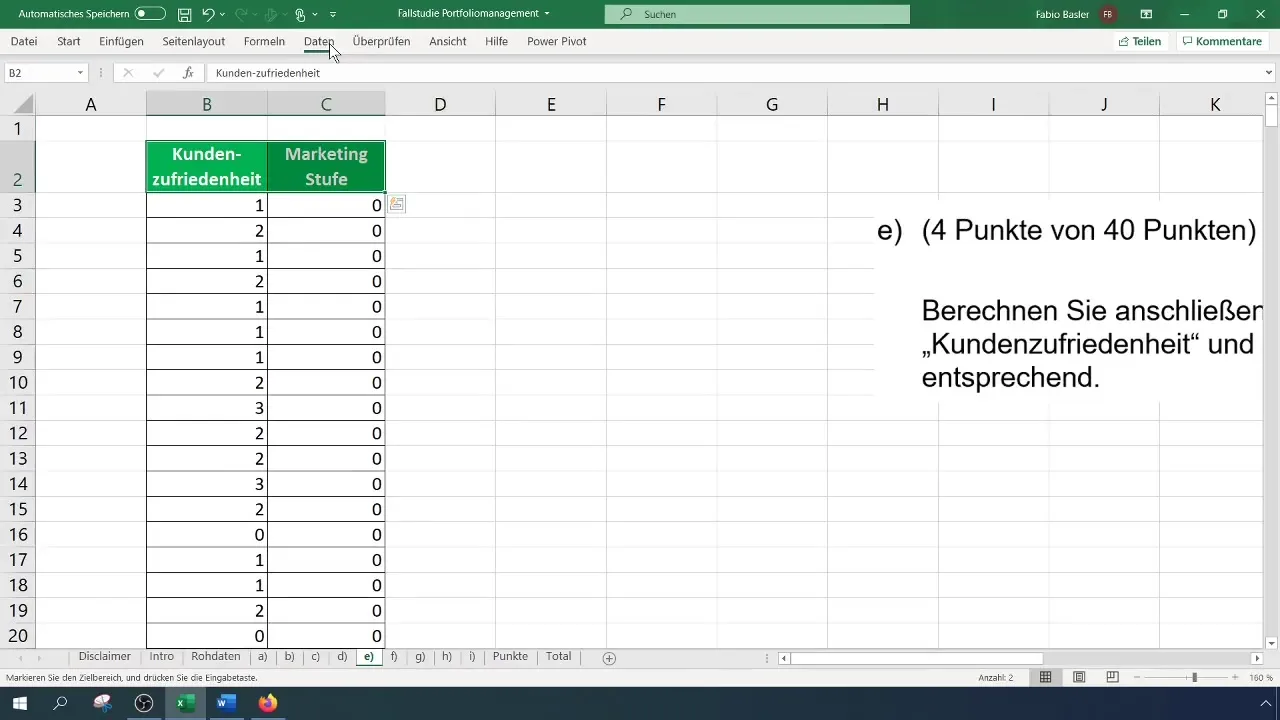
Järgmiseks on vaja ette valmistada andmeid reitingukorreleerivaks analüüsiks. Sul on vaja muutujate ränge. Excelis saab seda teha funktsioonide "RANG.GLEICH" või "RANG.MITTEL.W" abil. See funktsioon määrab igale arvule kindla maatriksi suhtes rea. Veendu, et töötad õiges vahemikus.
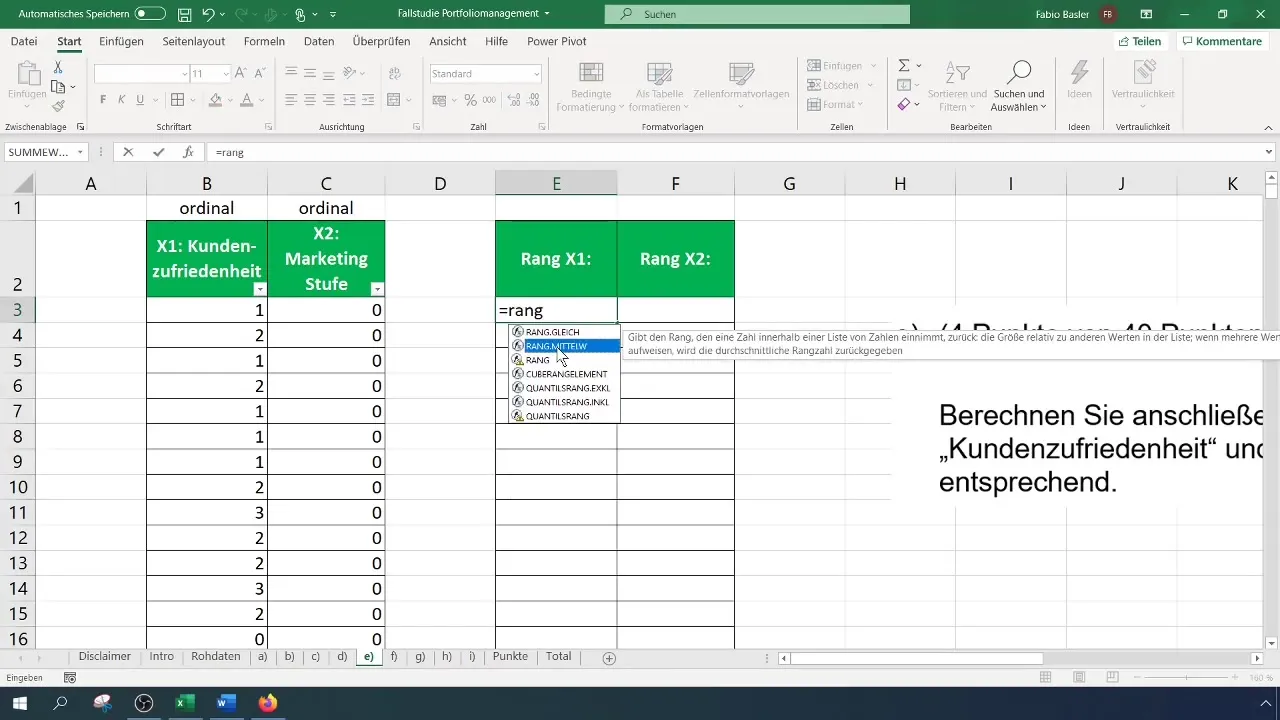
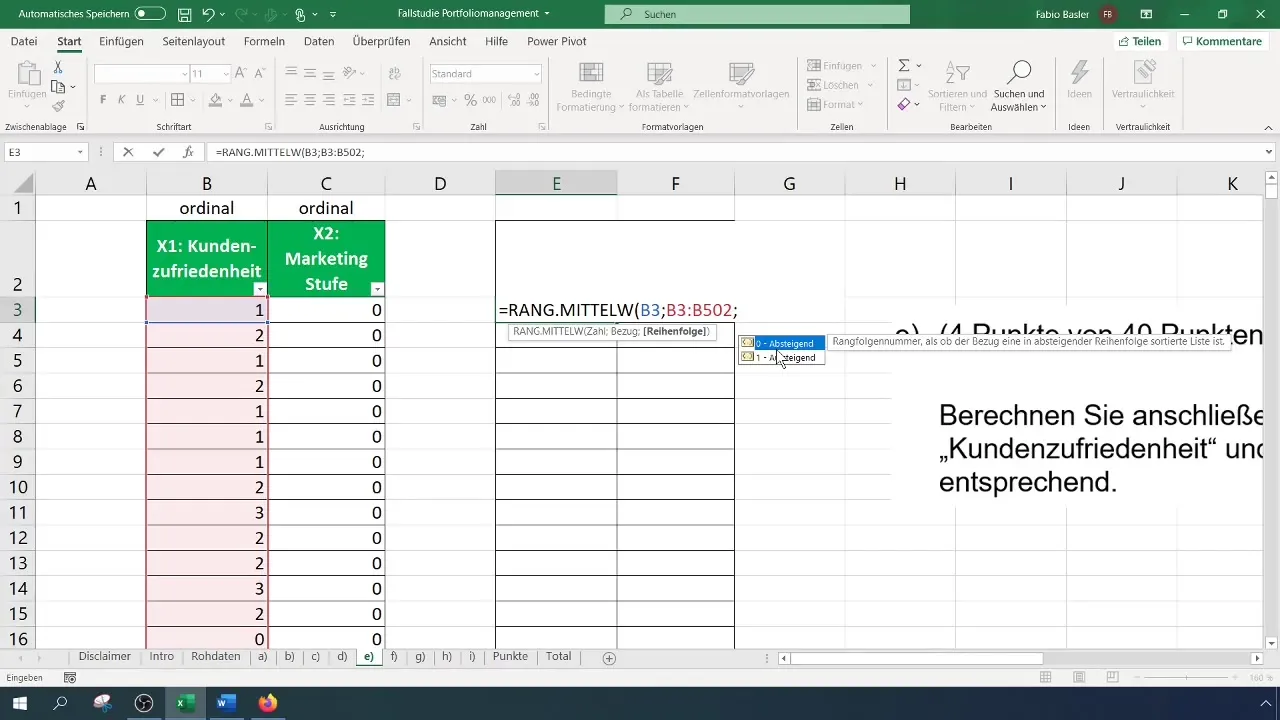
Kliendirahulolu ränkide arvutamiseks, mida me siin nimetame muutujaks X1, vali kõigepealt vastav lahtr. Esimese vaatluse jaoks tähendab see, et vali kliendirahulolu lahtr ja seejärel vali maatriks, kus ränge arvutatakse. Oluline on fikseerida viide kogu maatriksile, et see ei muutuks, kui valemid alla lohistad.
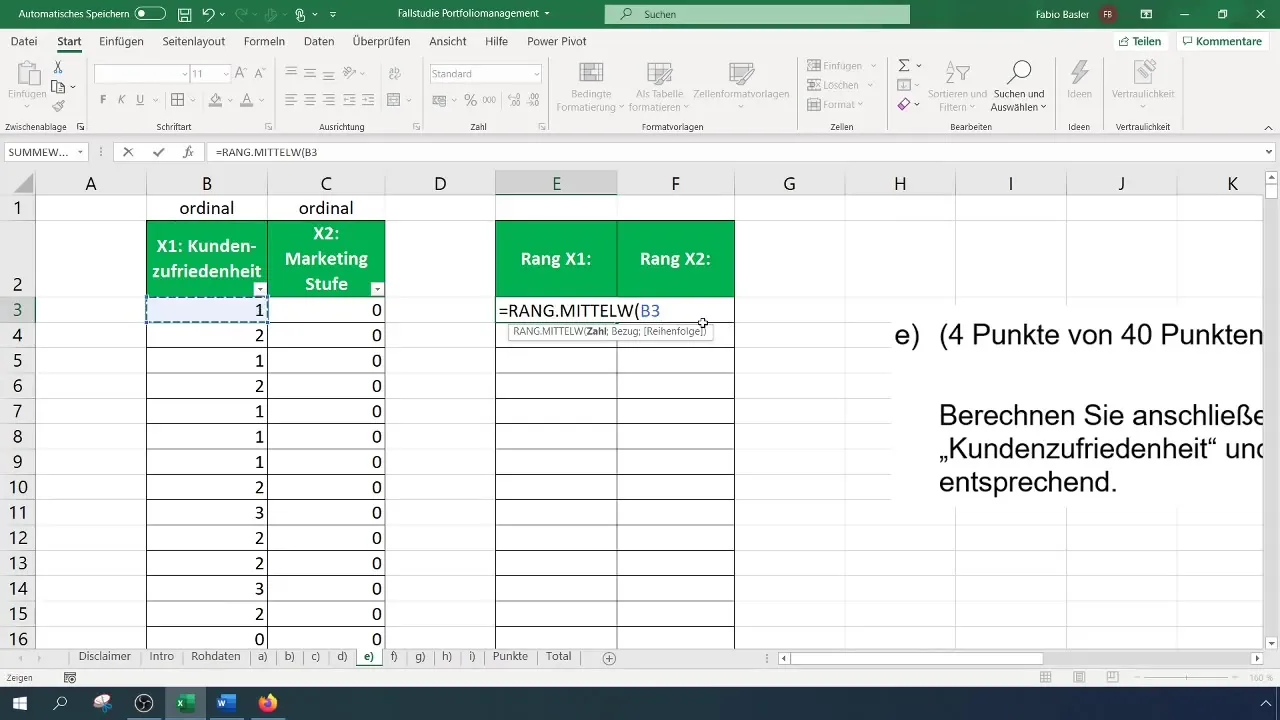
Alusta arvutamist, sisestades valemi ja lisades seejärel vastavad parameetrid. Jälgi, et järgid funktsioonis õiget järjestust. Määra viide oma andmemaatriksile ja vali soovitud sortimine, kas tõusvalt või laskuvalt.
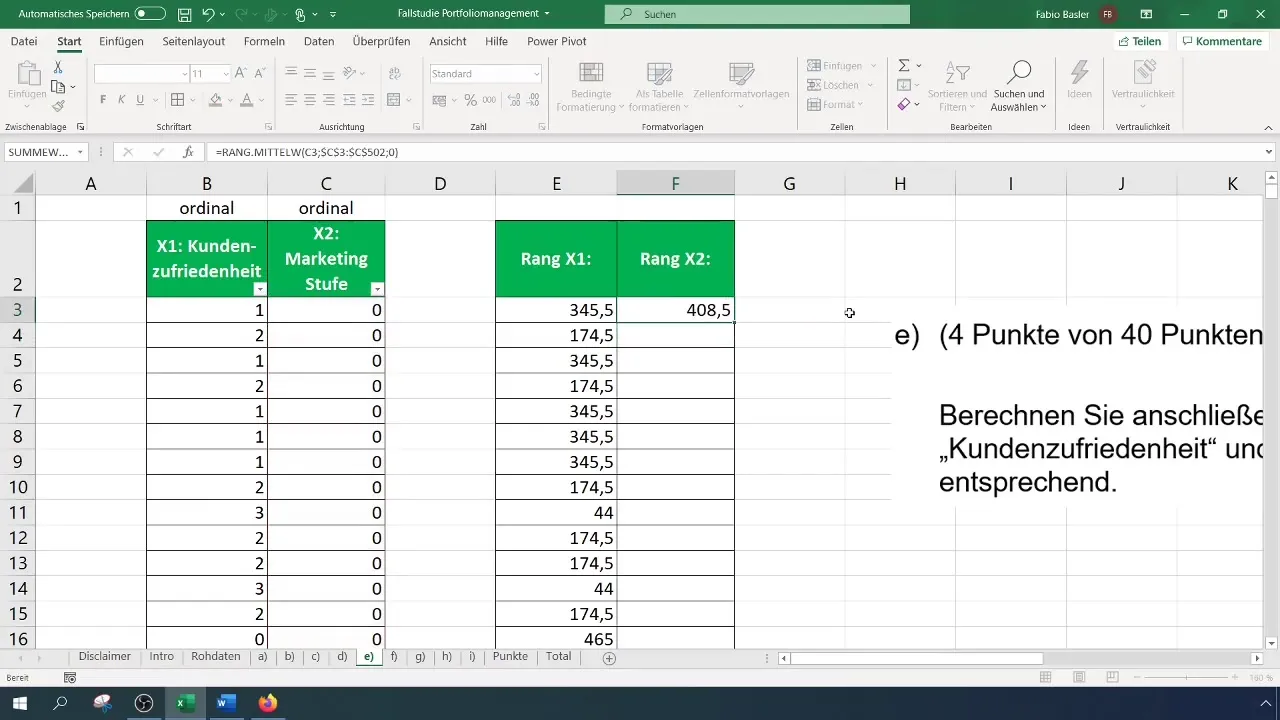
Kui soovid ränki turundustaseme jaoks (X2) arvutada, korda samu samme. Ka siin on oluline hoida kogu andmevahemik kindlalt kinni, et valem töötaks õigesti, kui selle alla kopeerid. Need sammud tagavad, et iga muutuja ränk määratakse korrektselt.
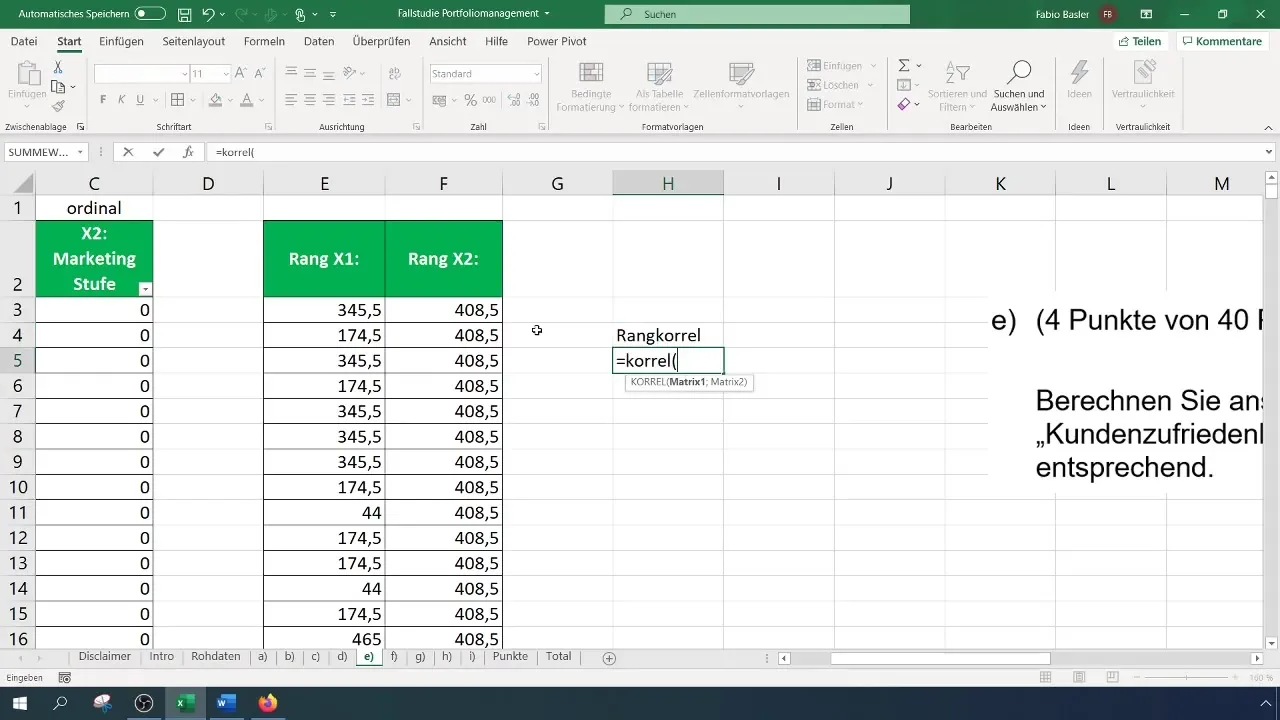
Kui sul on rändid mõlema muutuja jaoks, saad arvutada reitingukorrelatsiooni. Saad seda teha funktsiooniga "KORREL". See funktsioon võimaldab sul valida nii X1 kui ka X2 rändid ning arvutada korrelatsiooni. Tulemus näitab sulle seose tugevust kahe muutuja vahel.
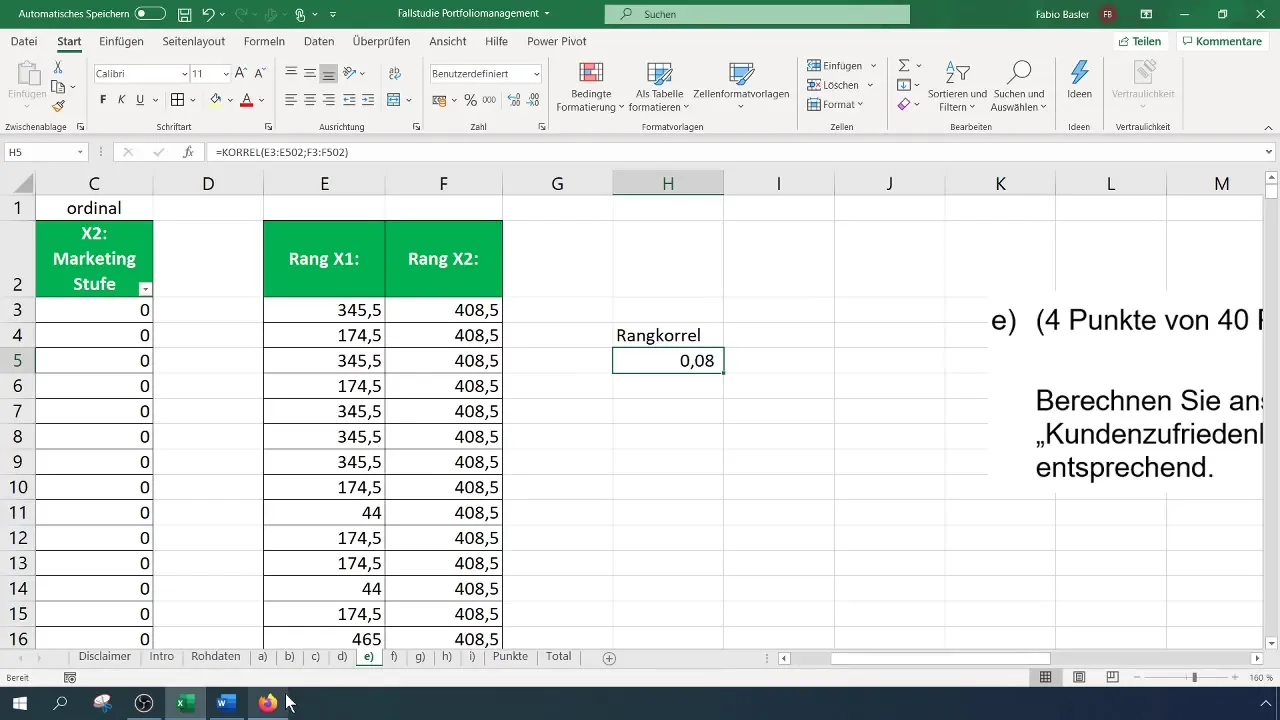
Sinu juhul on korrelatsioon 0,082, mis viitab nõrgale positiivsele seosele. See number näitab, et kuigi eksisteerib tendents, et suuremad turunduskulud viivad parema kliendirahuloluni, pole see seos siiski tugev.
Lõpuks peaksid tulemuste tõlgenduse dokumenteerima. Tabel võib sind aidata selgitada, kus reitingukorrelatsioon asub ja selgitada selgelt kahe muutuja vahelist suhet.
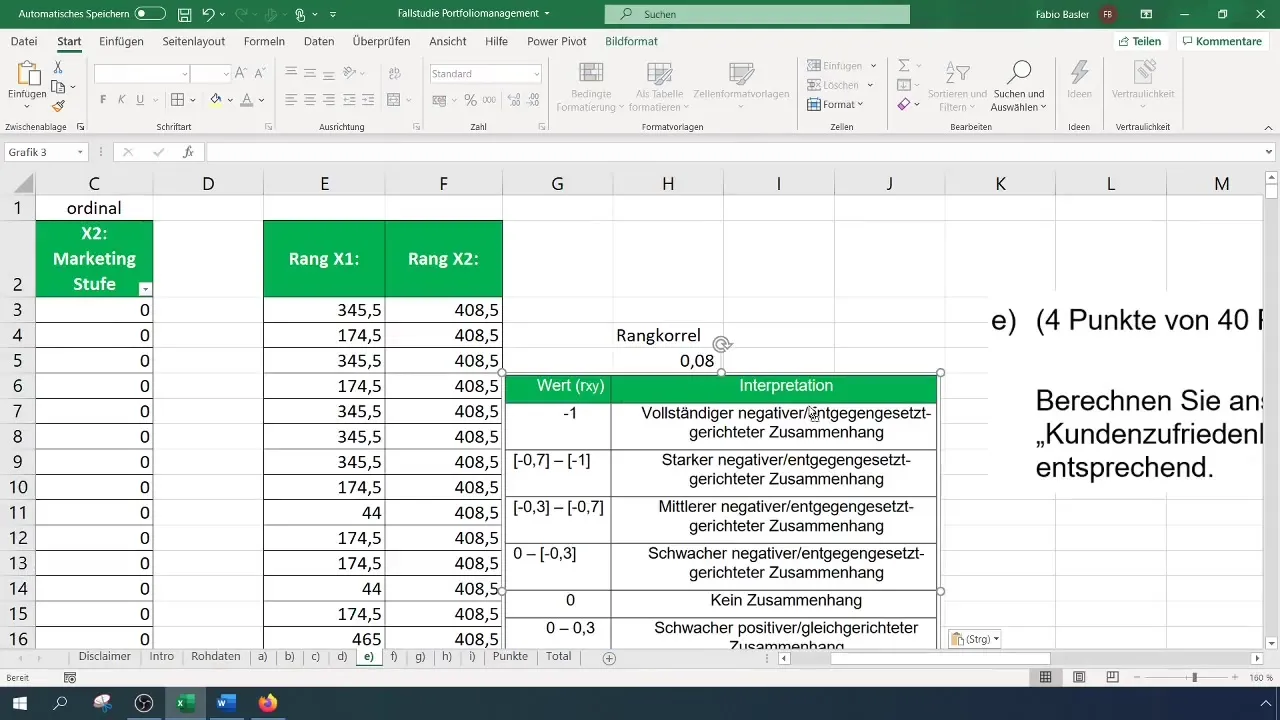
Rangkorrelatsioonianalüüsi lähenemisviis aitab saada kvalitatiivseid ülevaateid kvantitatiivsete andmete kohta ning näitab, kuidas turunduskulud võiksid varieeruda ilma otseselt klientide rahulolu suurendamata.
Kokkuvõte
Selles juhendis õppisid, kuidas teostada rangkorrelatsioonianalüüsi Excelis. Esiteks valmistasid oma andmed korrektselt ette ja seejärel määrasid mõlema muutuja järgud. Lõpuks arvutasid välja korrelatsiooni, et kvantifitseerida seost turundustaseme ja kliendirahulolu vahel.
Korduma kippuvad küsimused
Kui erinevad on Spearman ja Kendall?Spearman ja Kendall on mõlemad rangkorrelatsioonikordajad, mis arvutatakse erinevalt. Spearman põhineb järgude erinevustel, samas kui Kendall kasutab ühtluste ja mitteühtluste arvu.
Kuidas valida sobiv korrelatsioon?Valik sõltub andmete tüübist. Ordinaalselt skaalastatud andmete korral sobib Spearman, metriliste andmete korral kasutatakse sageli Pearsoni korrelatsiooni.
Kas ma võiksin korrelatsiooni asemel kasutada regressiooni?Jah, regressioon võib olla kasulik ühe või mitme sõltumatu muutuja mõju uurimiseks sõltuva muutuja kohta, korrelatsioon näitab vaid suhet.


