Statistilised analüüsid on hädavajalik tööriist portfellihalduses. Eriti võimas meetod on regressioonianalüüs, eriti kui on vaja kindlaks määrata mitme sõltumatu muutuja mõju ühele sõltuvale muutujale. Kas soovid teada, kuidas Excelis luua ja analüüsida lineaarset funktsionaalset seost mitme regressiooni kaudu? See juhend annab sulle selge ülevaate ning üksikasjaliku samm-sammult juhendi.
Olulisemad teadmised
- Regressioonianalüüs aitab kvantifitseerida sõltumatute muutujate mõju sõltuvale muutujale.
- Oluline on hinnata regressioonimudeli headust ja statistilist olulisust.
- Koefitsientide hindamise kaudu saab kindlaks teha, milline sõltumatu muutuja avaldab tugevamat mõju sõltuvale muutujale.
Samm-sammult juhend regressioonianalüüsiks Excelis
Andmete ettevalmistamine
Enne regressioonianalüüsi alustamist pead oma andmed ette valmistama. Selles juhul on sõltuv muutuja (y) sülearvutite müük ning sõltumatud muutujad (x1 ja x2) töötajate arv ja konkurentsiaktsioonide arv. Esiteks sisesta kõik vajalikud andmed Excelisse ja struktureeri need selgelt.
Korrelatsiooni kontrollimine
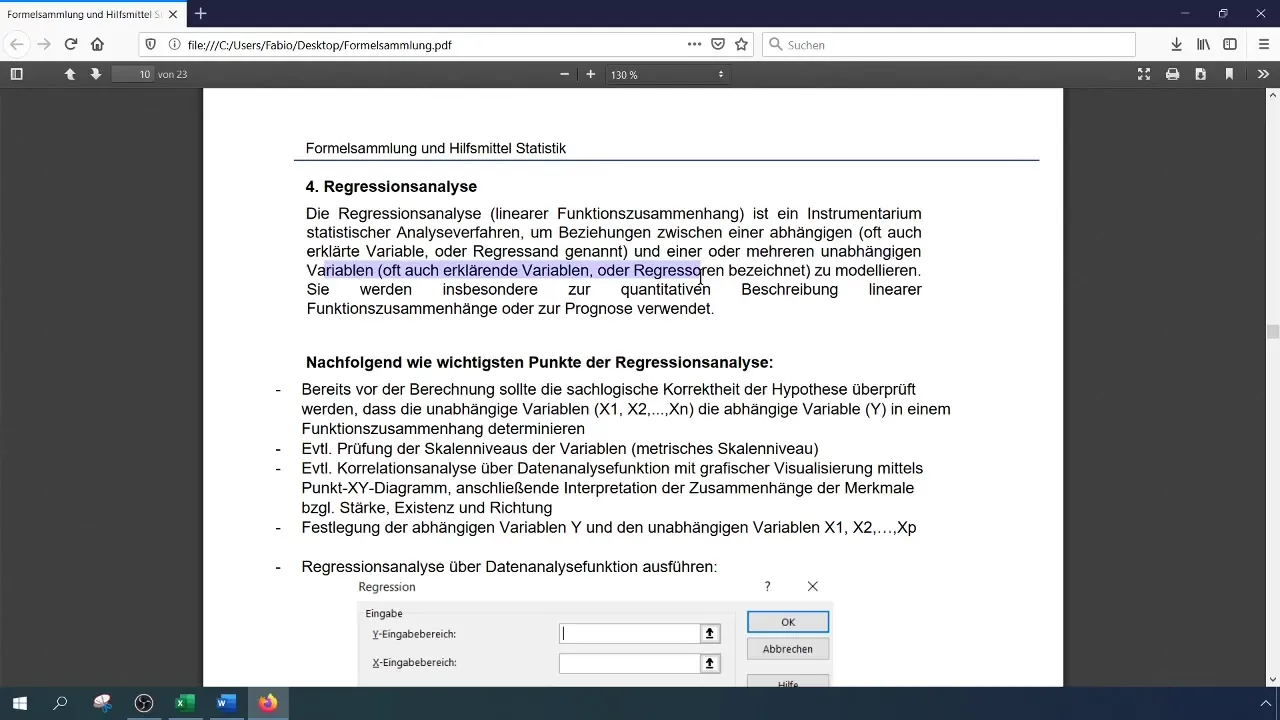
Esimene vihje võimalike seoste kohta muutujate vahel saamiseks on korrelatsioonimatriksi loomine. See matriks aitab näha, kui tugevad on erinevate muutujate omavahelised seosed. Seda saad teha Excelis funktsiooni "Andmeanalüüs" abil ning valida seejärel korrelatsioonimatriksi, hõlmates kõiki asjakohaseid andmevaldkondi.
Regressioonianalüüsi läbiviimine
Nüüdseks oled valmis regressioonianalüüsi läbi viima. Vali taas funktsioon "Andmeanalüüs", seejärel vali "Regressioon". Siin määra sõltuva muutuja (sülearvutite müük) ja sõltumatute muutujate (töötajate arv ja konkurentsiaktsioonide arv) sisendvaldkond.
Tulemuste tõlgendamine
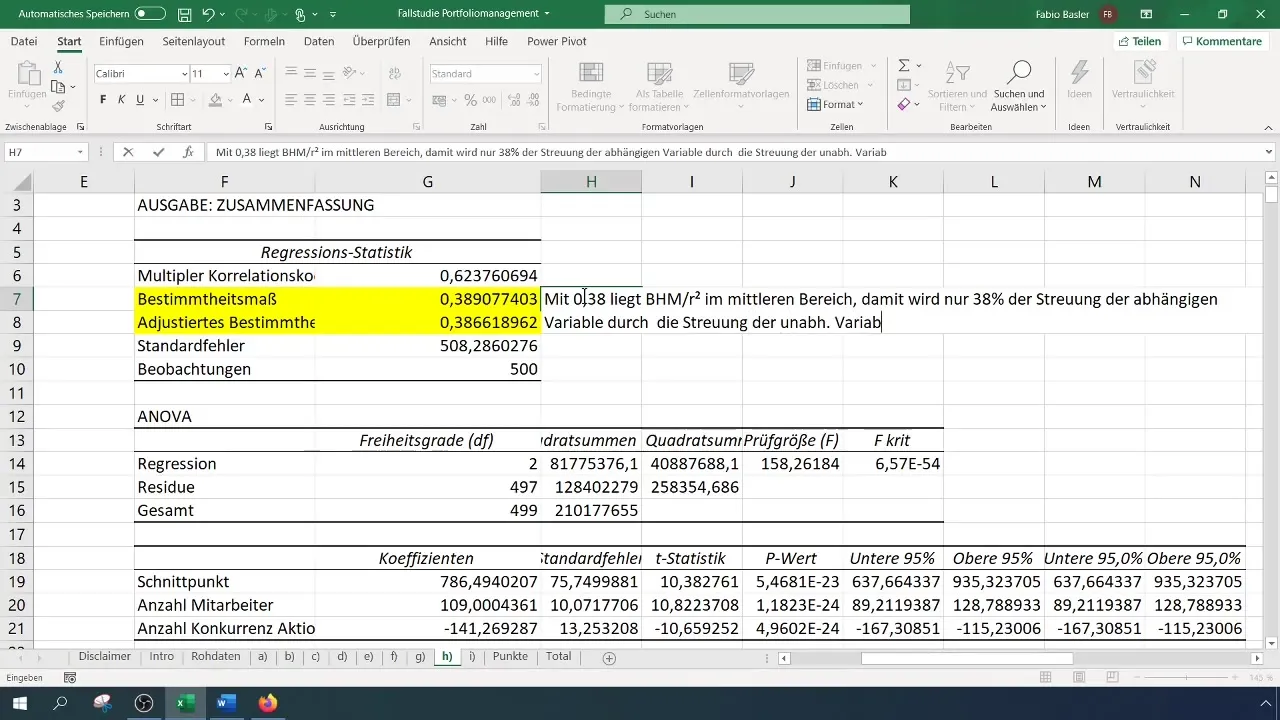
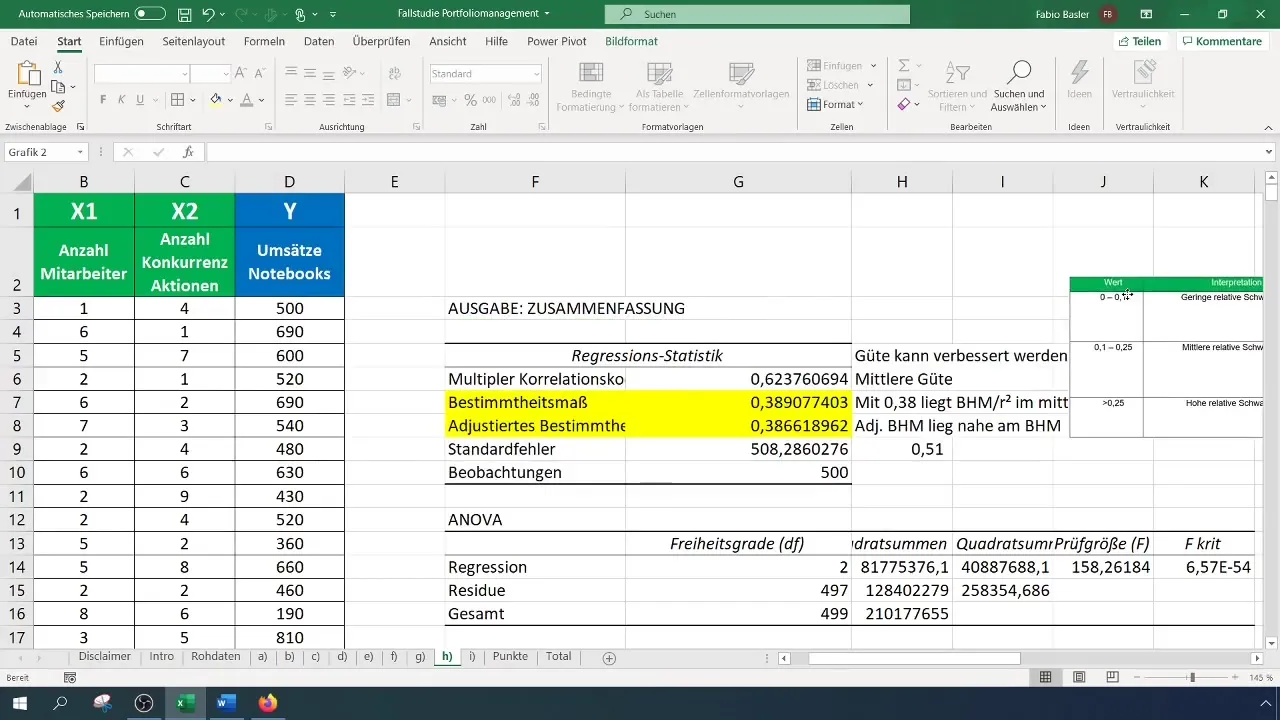
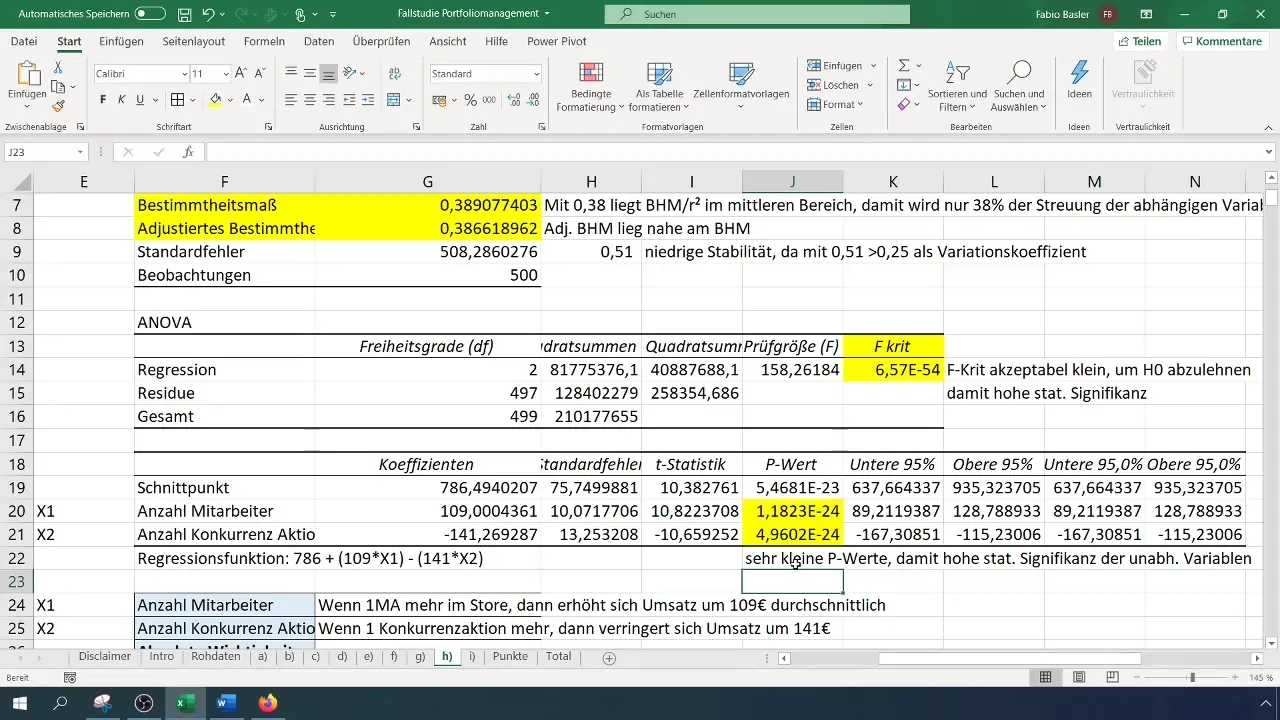
Regressioonianalüüsi läbiviimise järel saad mitmesuguseid väljundeid ja statistikat. Esimene oluline punkt on selgitusmäära (R²), mis kirjeldab sõltuva muutuja seletamise osakaalu sõltumatute muutujate poolt. R² väärtus 0,38 näitab, et 38% müügi muutlikkusest saab seletada nende kahe sõltumatu muutuja abil.
Hindamise käigus pane tähele, kui stabiilne mudel on. Selleks võid kasutada stabiilsuse hindamiseks standardviga. Näiteks kui saad standardvea 0,51, näitab see suurt suhtelist kõikumist ja seega madalat stabiilsust.
Tugevate mõjufaktorite hindamine
Otsustava sammu tegemine on välja selgitada, millisel sõltumatul muutujal on sõltuva muutuja suhtes tugevam mõju. Seda saad teha koefitsientide abil, mis näitavad muutujate absoluutset olulisust. Siin on x1 (töötajate arv) koefitsient 109, samas kui x2 (konkurentsiaktsioonide arv) koefitsient on -141. See näitab, et igal töötajate arvu suurenemisel tõuseb müük 109 euro võrra, samal ajal kui iga konkurentsiaktsioonide arvu suurenemine vähendab müüki 141 euro võrra.
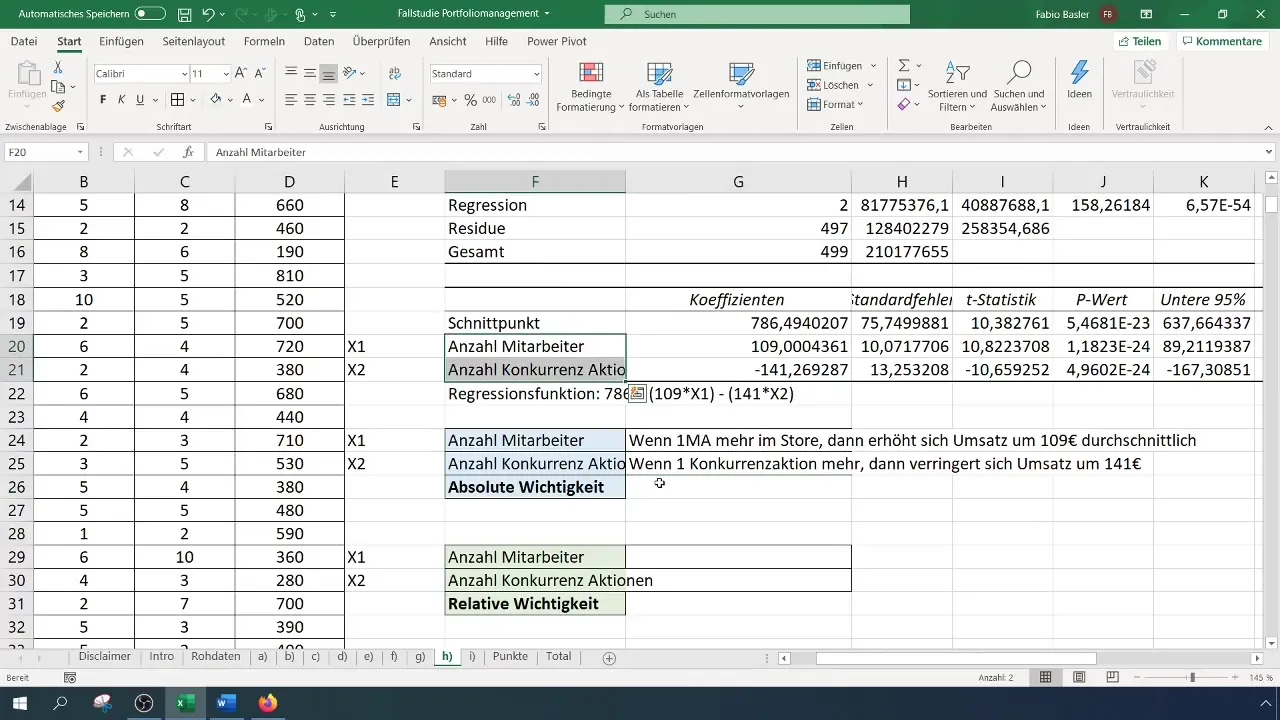
Statistilise olulisuse hindamine
Veel üks oluline aspekt regressioonianalüüsis on statistiline olulisus. Seda saab näha p-väärtuste ja F-testiga, mis mõlemad peaksid olema väga madalad. See näitab, et sõltumatutel muutujatel on oluline mõju sõltuvale muutujale ja õigustab mudeli kasutamist.
Kokkuvõte
Regressioonianalüüs Excelis võimaldab teil kvantitatiivselt hinnata erinevate muutujate vahelist seost. Selle juhendi abil saite teada, kuidas läbi viia ja tõlgendada mitmeid regressiooni. Hindage kriitiliselt mudeli headust ja stabiilsust ning üksikuid mõjufaktoreid, et teha portfellihalduses teadlikke otsuseid.
Korduma kippuvad küsimused
Milliseid andmeid ma vajan regressioonianalüüsiks?Sul on vaja sõltuvat muutujat (nt käive) ja vähemalt ühte või mitut sõltumatut muutujat (nt töötajate arv, konkurentsitegevus).
Kuidas tõlgendada määramatusmõõdet R²?Suurem R²-väärtus tähendab, et suurem osa sõltuva muutuja muutlikkusest on seletatav sõltumatute muutujate poolt.
Kuidas saan kontrollida statistilist olulisust?Saad kasutada p-väärtusi ja F-testi; madalad väärtused viitavad suurele olulisusele.
Mis vahe on R² ja kohandatud R² vahel?Kohandatud R² arvestab sõltumatute muutujate arvu ja pakub realistlikumat hinnangut mudelite puhul, kus on mitu muutujat.
Kuidas saan mõjufaktorite tugevust hinnata?Seda tehakse, vaadates sõltumatute muutujate kordajaid, mis kvantifitseerivad iga muutuja mõju sõltuvale muutujale.


