Rangkorrelatsioonianalüüsid on olulised statistiliste suhete uurimisel muutujate vahel. Eriti kui tegemist on järjestuslikult skaalaga andmetega, on Spearmani rangkorrelatsioon kasulik meetod mustrite ja seoste avastamiseks. Selles juhendis õpid samm-sammult, kuidas Excelis kasutades teha Spearmani rangkorrelatsiooni arvutusi küsitluse jaoks.
Põhilised järeldused
- Rangkorrelatsioon mõõdab monotoonse suhte tugevust ja suunda kahe järjestusliku muutuja vahel.
- Spearmani rangkorrelatsioonikordaja on eriti sobiv, kui üks muutujatest on järjestuslik ja teine meetriliselt skaalal.
- Excelis arvutamine võib toimuda lihtsate valemite ja funktsioonide abil.
Samm-sammult juhend
Esmalt määratleme muutujad, mida soovime analüüsida. Selles näites on tegemist klientide rahuloluga (järjestuslik skaala, väärtused 1-3) ja tellimuste arvuga (meetriliselt skaalal).
Oma rahulolu ja tellimuste arvu jaoks järjekorra loomiseks vajad tabelit, kus on vastavad andmed. Veendu, et sisestad need andmed Excelisse.

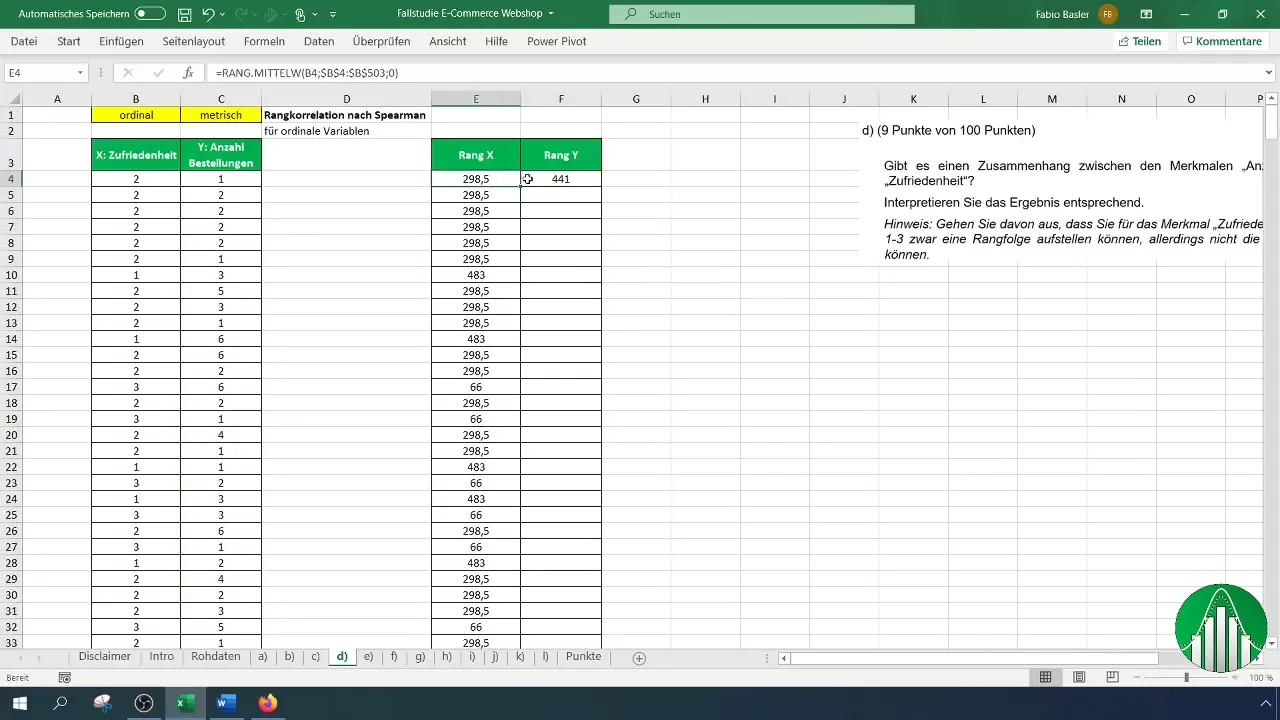
Pärast andmete sisestamist Excelisse vaatame Spearmani rangkorrelatsiooni arvutamist. Selleks kasutame Excelis funktsiooni "RANG.KESK", mis annab numbri järjestuses antud arvu jaoks. Rahulolu jaoks kasutame esialgu järgmist valemit:
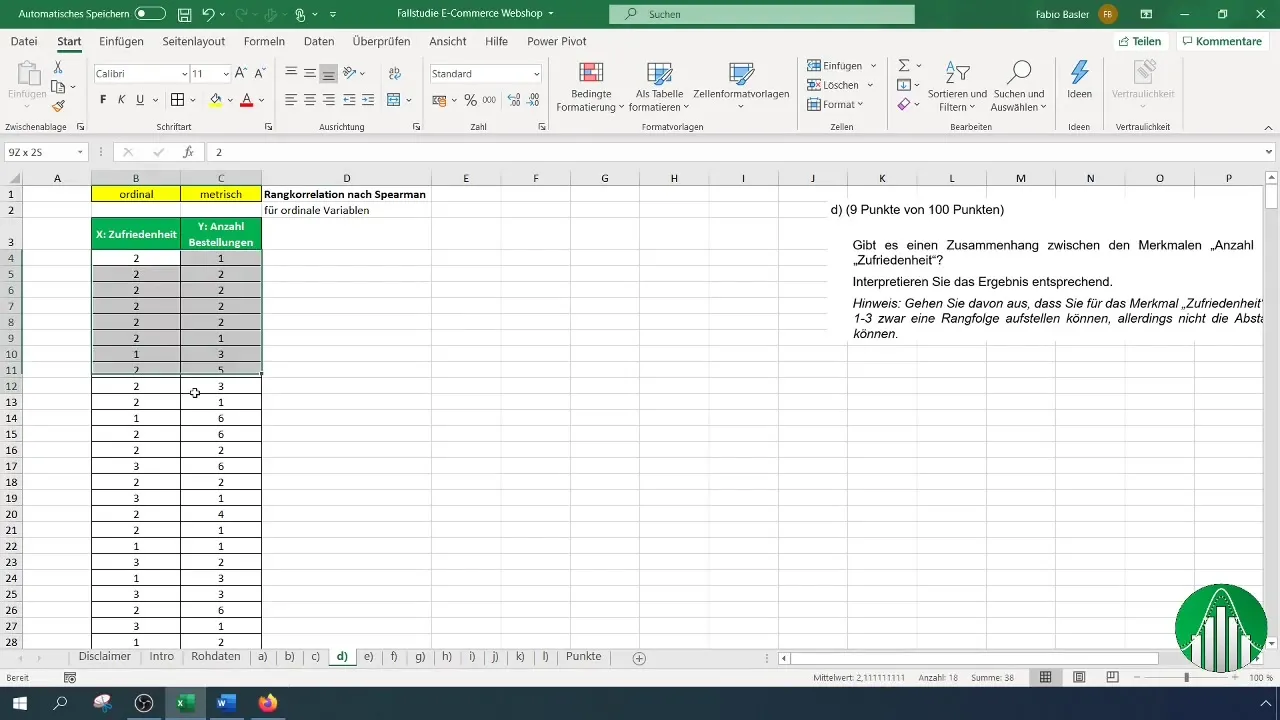
Valemi kasutamisel pea meeles, et märgid järjestuse rahulolu ja kinnita andmehulga komplekti B4-st kuni andmesarja lõpuni, et täpselt tuvastada rangid.
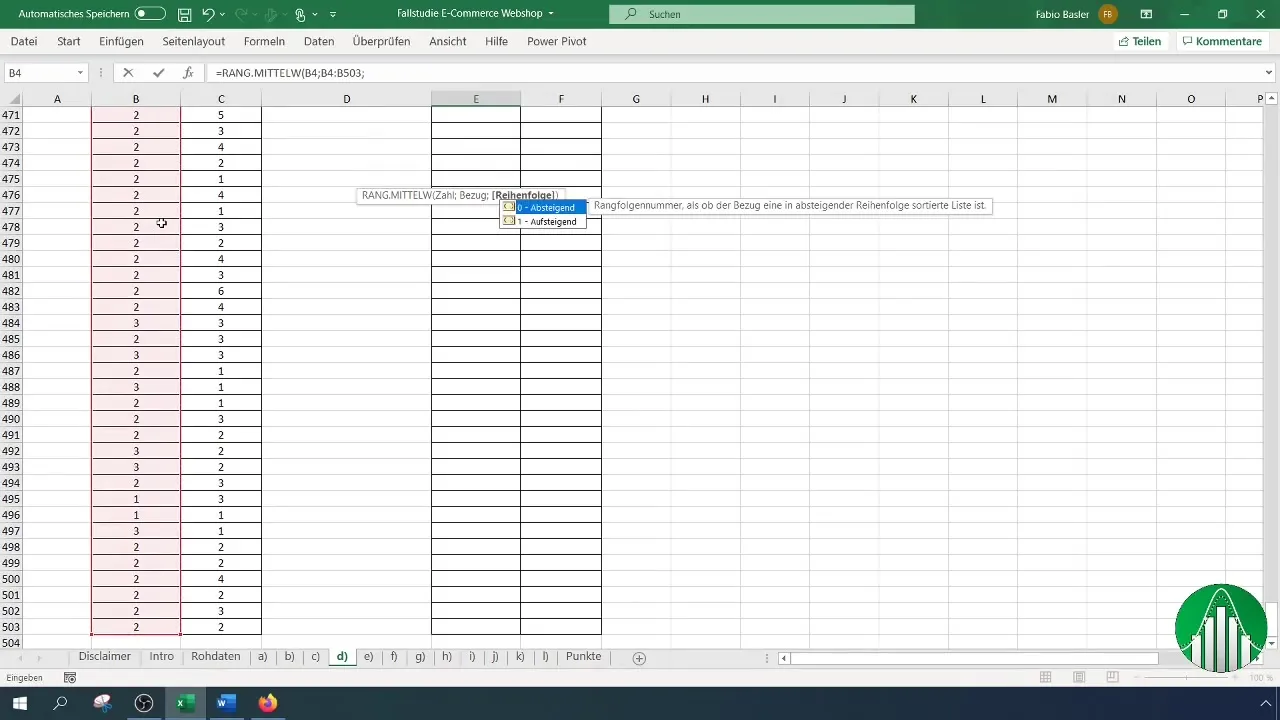
Otsusta, kas soovid rangid järjestada tõusvalt või laskuvalt. Tavaliselt on soovitatav neid järjestada tõusvas järjekorras. Oluline on fikseerida rangide jaoks rakus viiteid, kasutades F4-klahvi. See on oluline, et viited jääksid kopeerimise ajal muutmata.
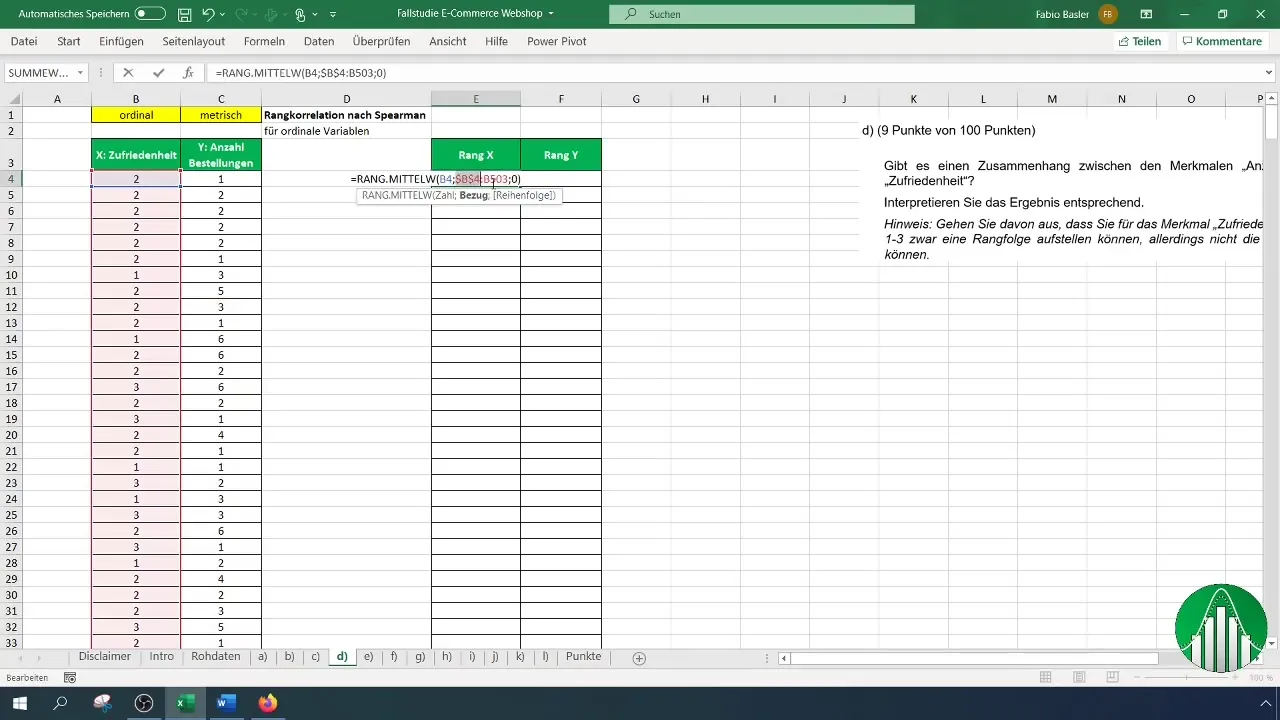
Kui oled rahulolu rangid määranud, korda protsessi tellimuste arvu jaoks. Veendu, et valemit ja viidet rakendad õigesti.
Mõlema rangi loendi (rahulolu ja tellimuste arv) korral oled valmis Spearmani rangkorrelatsioonikordinaadi arvutamiseks. Selleks kasuta valemit "=KORREL", et suhet määrata. Süntaks näeb välja järgmiselt:
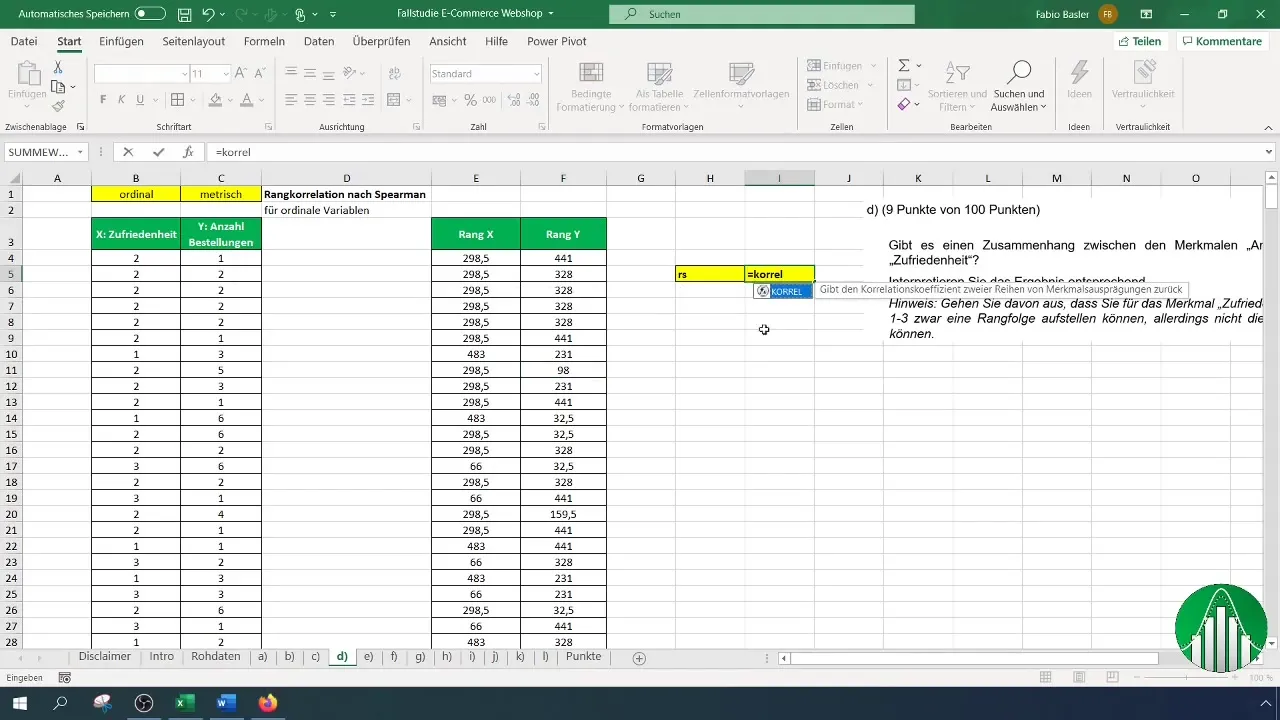
Esimene viide on rahulolu rangiloend ja teine tellimuste rangiloend. Excel arvutab nüüd automaatselt Spearmani rangkorrelatsioonikordinaadi.

Mis on sinu arvutuse tulemus? 5,61% väärtus näitab nõrka positiivset seost rahulolu ja tellimuste arvu vahel. See tähendab, et nende kahe muutuja vahel praktiliselt puudub oluline seos.
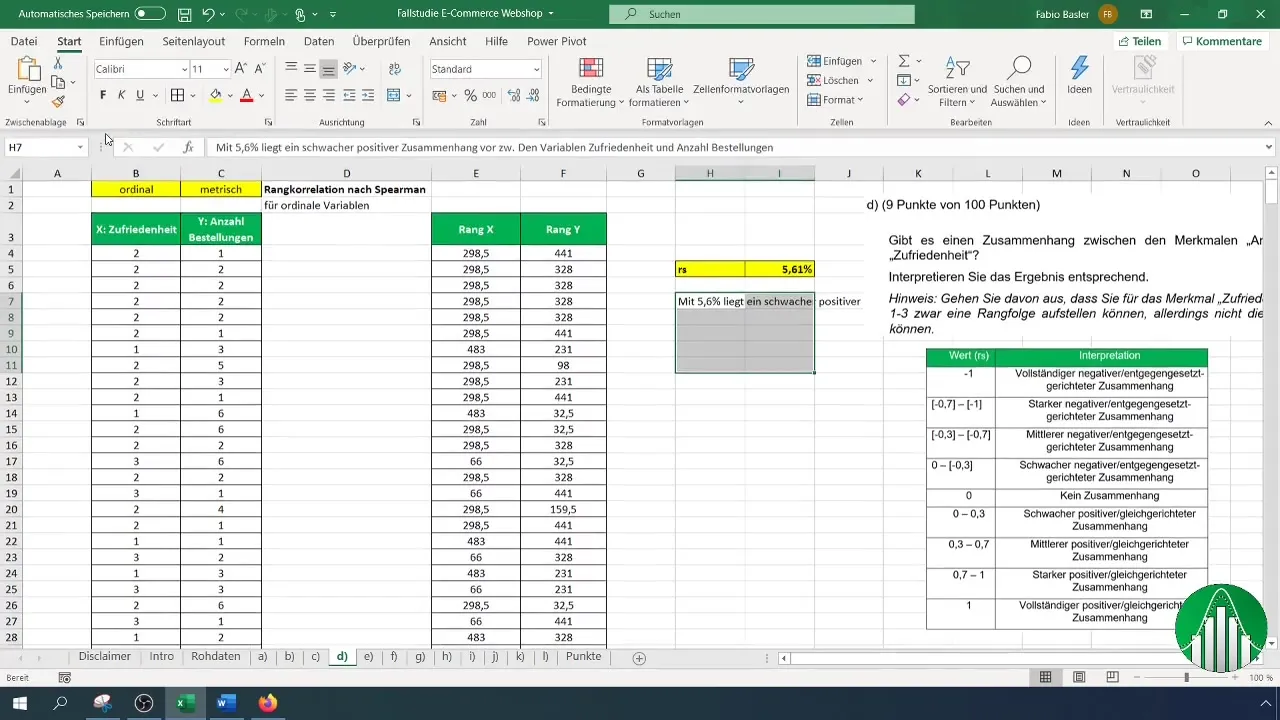
Tulemuste tõlgendamiseks kasuta väärtustabelit, kus on loetletud rangkorrelatsiooni erinevad valdkonnad. Pärast tõlgendamist kinnitame, et madal korrelatsiooni määr tähendab, et muutujad on suhteliselt sõltumatud.
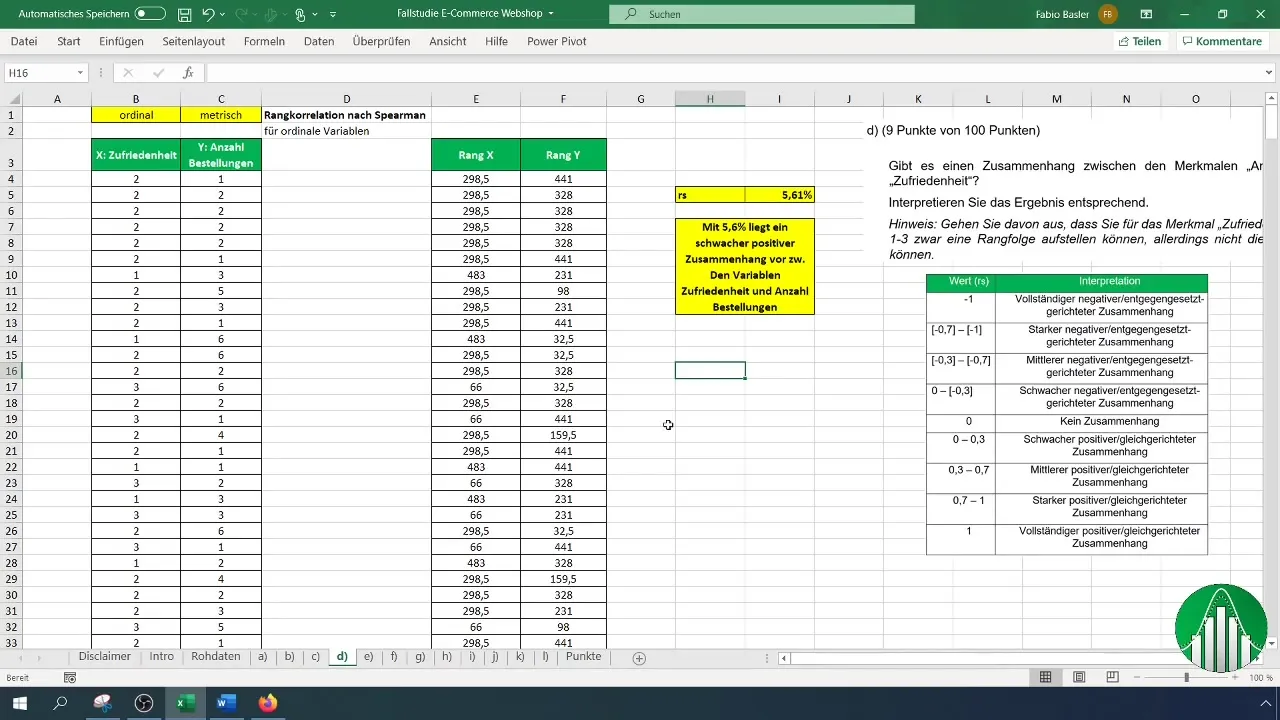
Kokkuvõte
Spearmani rangkorrelatsioonianalüüs Excelis võimaldab teil saada väärtuslikke teadmisi järjestuslike ja mõõdetavate muutujate suhetest. Meetod on lihtne ja annab selge ülevaate võimalikest seostest.
Korduma kippuvad küsimused
Mis on Spearmani järjestuskorrelatsioonikordaja?Spearmani järjestuskorrelatsioonikordaja mõõdab kahe muutuja vahelise monotoonse seose tugevust ja suunda.
Millal on mõttekas kasutada Spearmani kordaja?See on mõttekas, kui vähemalt üks muutuja on järjestuslikult skaalaline.
Kuidas arvutan Excelis Spearmani kordaja?Kasuta ridade keskmiste järjestuste määramiseks funktsiooni "RANG.KESKMINE" ja seejärel seose arvutamiseks funktsiooni "KORREL".
Mis vahemikus kehtib Spearmani kordaja?Kordaja on vahemikus -1 kuni 1. Väärtused lähedal 1 viitavad tugevale positiivsele korrleatsioonile, samas kui väärtused lähedal -1 viitavad tugevale negatiivsele korrelatsioonile.
Mis võib tähendada 5,61% väärtus järjestuskorrelatsioonis?Väärtus 5,61% näitab nõrka positiivset seost, mis viitab sellele, et muutujad on suhteliselt sõltumatud.


