Excel-perusteet: Oppia ymmärtämään absoluuttiset soluviittaukset

Solusijaksot Excelissä voivat helpottaa ja tehostaa työskentelyäsi huomattavasti. Tunnet varmasti suhteelliset solusijainnit. Mutta miten on laita absoluuttisten solusijojen kanssa? Ne ovat olennainen osa tarkkoja laskelmia Excel-taulukoissasi, ilman että sijainti muuttuu kaavojasi kopioitaessa. Tutkitaan yhdessä eroja suhteellisten ja absoluuttisten solusijojen välillä.

Tärkeimmät havainnot

• Absoluuttiset solusijainnit pysyvät paikallaan eivätkä muutu kaavoja kopioitaessa.
• Absoluuttiset solusijainnit määritellään dollarimerkillä ($).
• Voit asettaa kiinnityksen yksilöllisesti sarakkeelle, riville tai molemmille.

Askeleittainen ohje

1. Excel-taulukon valmistelu

Aluksi luot uuden tyhjän Excel-taulukon. Ensimmäiseen riviin voit syöttää erilaisia arvoja. Esimerkiksi oletetaan, että sinulla on 500 € pääomaa, jota haluat käyttää erilaisiin ostoksiin.

2. Menojen syöttäminen

Syötä niihin soluihin arvot, jotka haluat käyttää ostoksiin. Esimerkiksi oletetaan, että käytät 50 euroa Rewellä, 80 euroa Marketkaupassa ja 130 euroa Saturissa.

3. Jäljellä olevan pääoman laskeminen

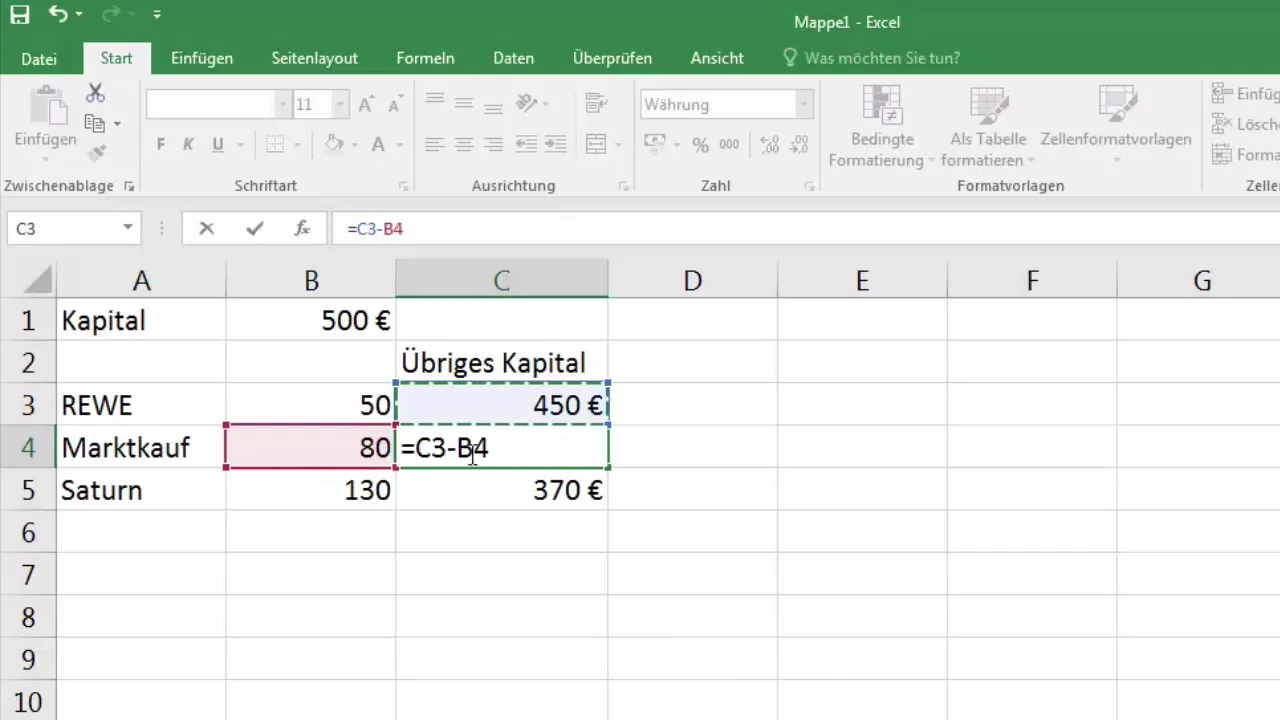
Nyt haluamme laskea jäljellä olevan pääoman jokaisen ostoksen jälkeen. Voit luoda uuteen soluun kaavan, joka laskee, paljonko pääomaa on jäljellä Rewen ostoksen jälkeen. Kaava olisi =B1-B3, missä B1 on alun perin oleva pääomasumma ja B3 on Rewessä käytetty summa.

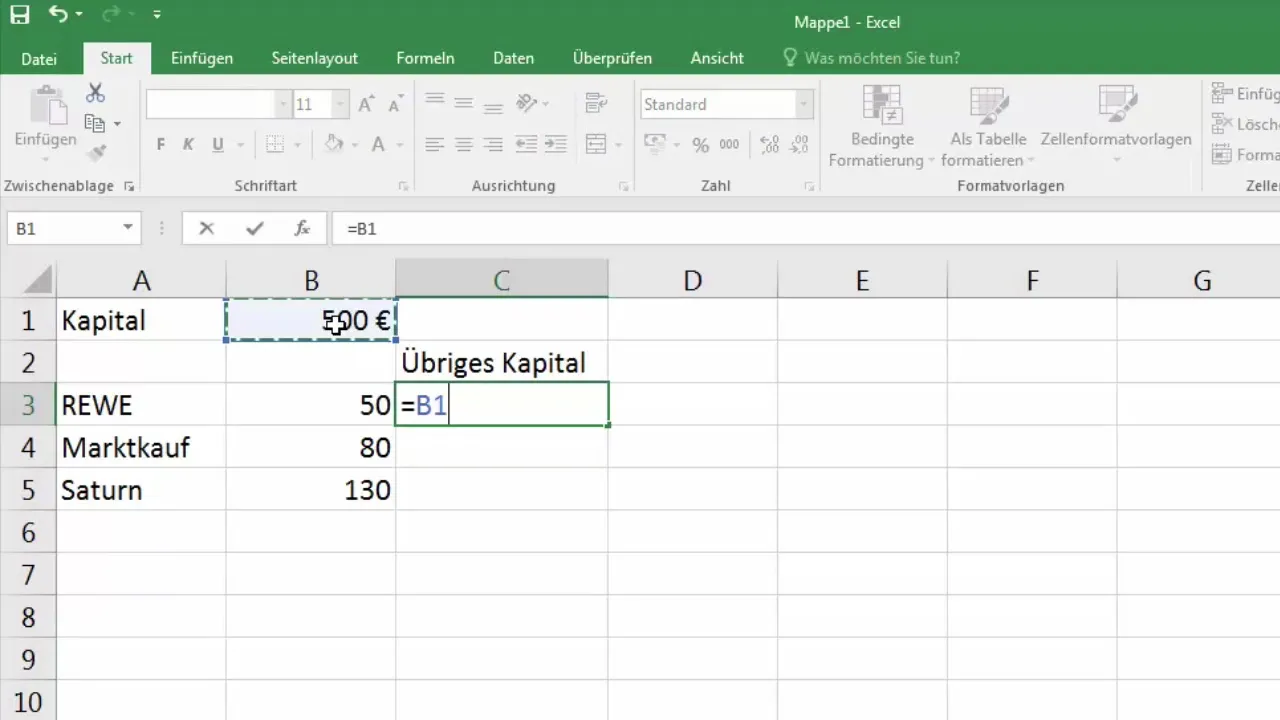
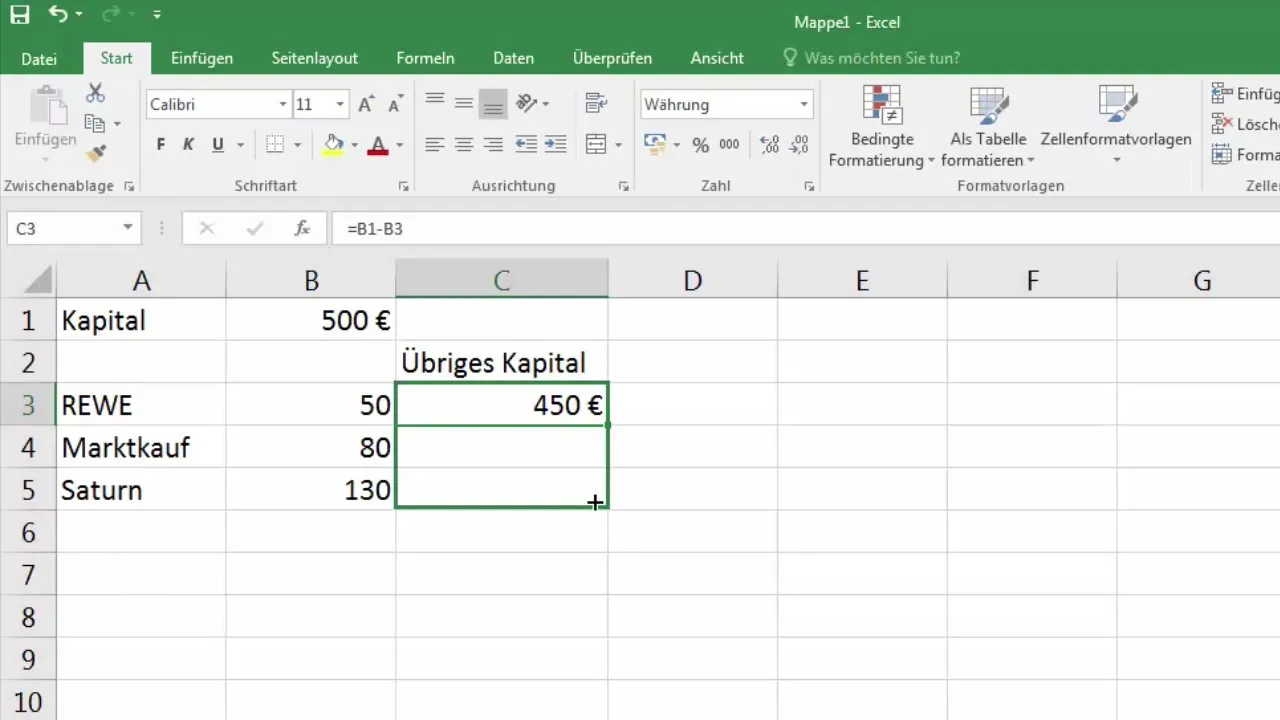
4. Kaavan kopioiminen ja suhteellisten sijaintien havainnointi

Nyt vedät solun, jossa kaava lasketaan, alaspäin. Tulet huomaamaan, että arvot muuttuvat ja viittaukset eivät ole oikeita. Tässä tulee mukaan suhteellisten ja absoluuttisten solusijojen ero.

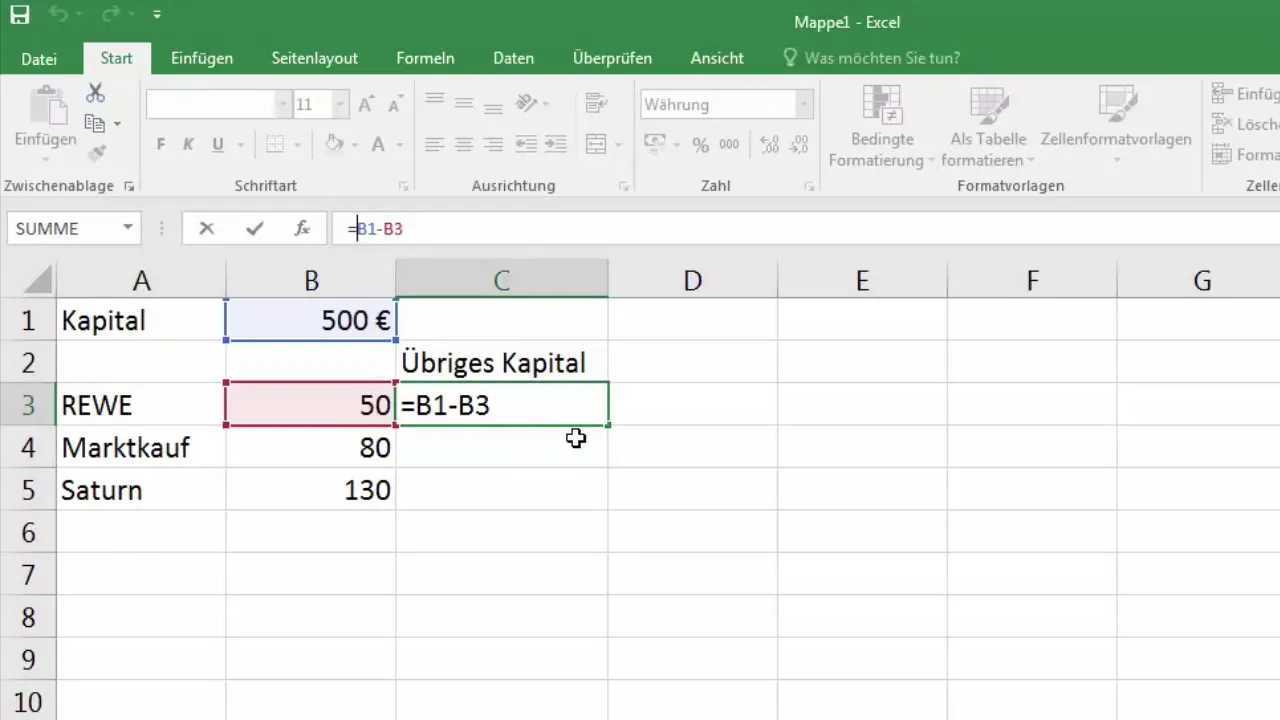
5. Absoluuttisen solusijan käyttöönotto

Varmistaaksesi, että viittaus pääomaasi B1 pysyy aina samana, voit määrittää tämän solun absoluuttiseksi solusijaksi. Tämä tapahtuu asettamalla dollarimerkit sarakkeen ja rivin nimityksen eteen. Sitä kutsutaan $B$1, mikä kiinnittää solun paikalleen.

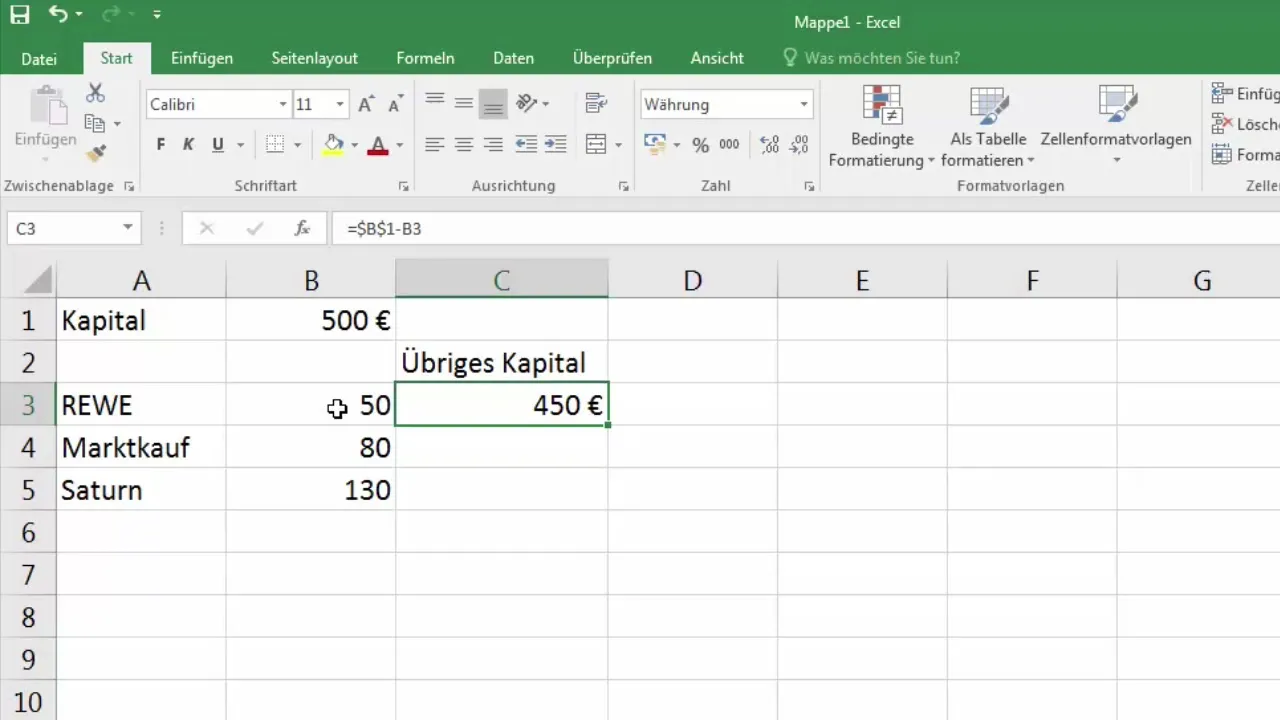
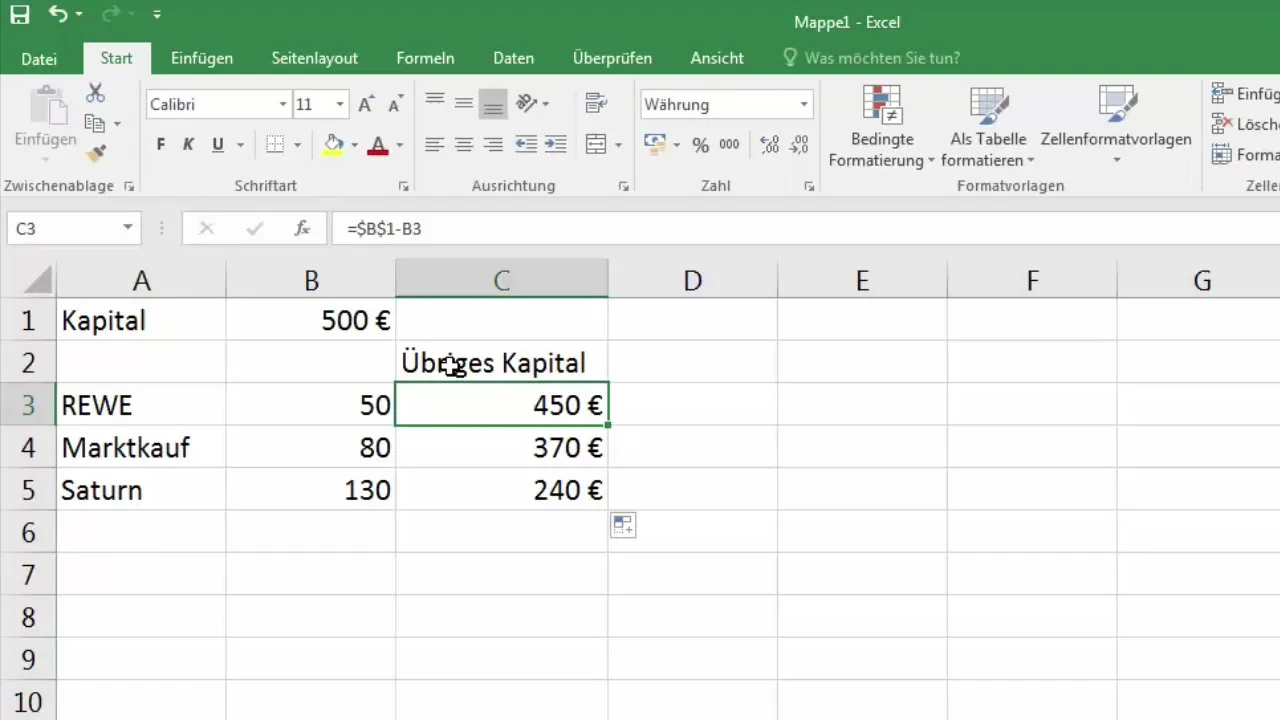
6. Kaavan muokkaaminen absoluuttisella sijainnilla

Nyt muutat kaavasi muotoon =$B$1-B3. Tämä johtaa siihen, että kaavaa kopioitaessa alaspäin viitataan aina arvoon B1, mikä tuottaa nyt oikeat tulokset.

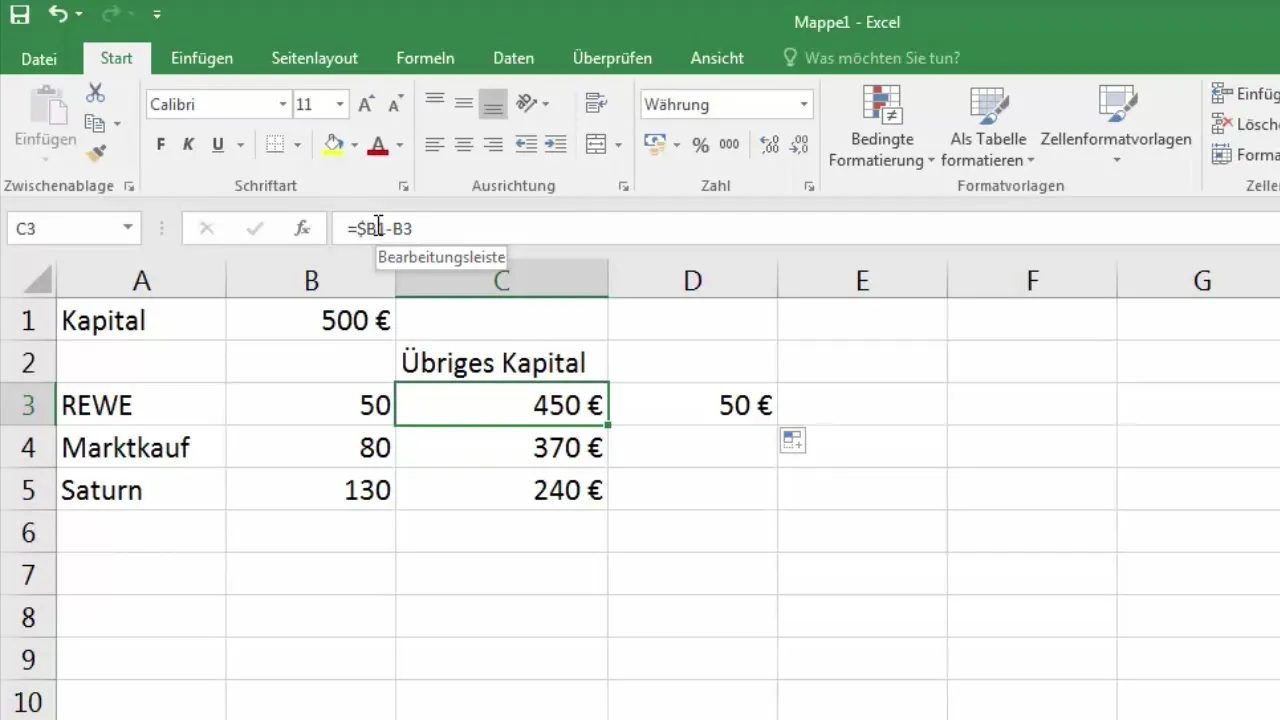
7. Laskevat laskelmat riviviitteellä

Jos haluat muotoilla laskelmat siten, että aina vähennetään edellisen rivin summa, voit tehdä sen samalla tavalla. Sen sijaan kirjoitat C3:een kaavan =C2-$B$1. Näin laskenta osoittaa suoraan nykyisen rivin yläpuolella olevaan soluun ja vähentää summan B1:ssä.

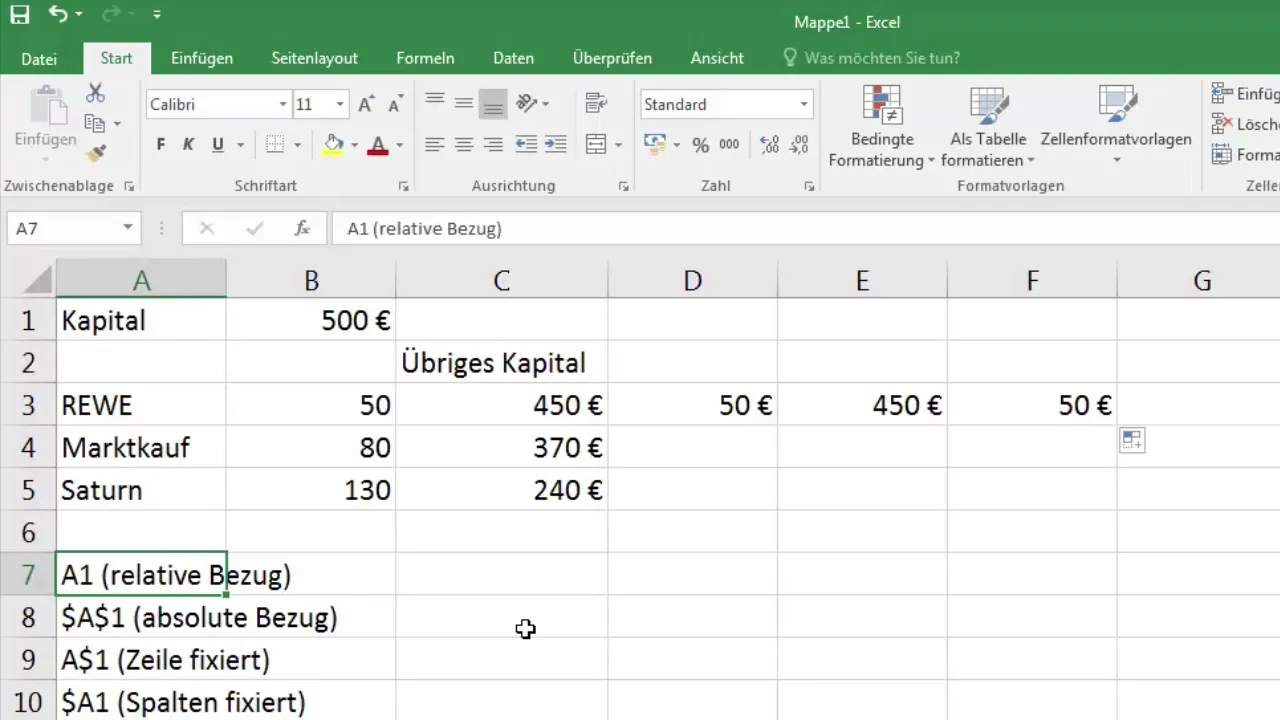
8. Lisälaskelmat ja dollarimerkkien käyttö

Jos jatkat laskelmien tekemistä tällä tavalla, voit hyödyntää dollarimerkkejä asianmukaisesti kiinnittääksesi joko rivin tai sarakkeen tai molemmat. Tämä antaa sinulle suurimman joustavuuden laskelmissasi.

9. Kaavojen kopiointi oikealle

Kun kopioit kaavoja oikealle, sarake B (§B$) pysyy kiinnitettynä. Kaikki muut viittaukset ovat edelleen suhteellisia, mikä antaa sinulle suurta etua suurempien tietomäärien tai jatkuvien laskelmien yhteydessä.

10. Yhteenveto soluviittausten käytöstä

Päätelmänä on välttämätöntä ymmärtää suhteellisten ja absoluuttisten soluviittausten erot voidakseen hyödyntää Excelin täyttä potentiaalia. Olitpa sitten käsittelemässä taloustietoja, myyntilukuja tai muita tilastoja - näiden soluviittausten oikea käyttö voi merkittävästi helpottaa analyysiäsi ja raportointiasi.

Yhteenveto

Olet nyt oppinut Excelin absoluuttisten soluviittausten perusteet. Tämä taito mahdollistaa tehokkaampien ja virheettömien laskutoimitusten suorittamisen, kun järjestät ja analysoit tietojasi.