Tilastotiede on tärkeä työkalu analysoinnissa monilla aloilla. Tämä ohje näyttää sinulle, kuinka teet Spearmanin järjestyskorrelaatioanalyysin Excelissä. Tällä menetelmällä voit tehokkaasti kvantifioida ordinaalimuuttujien välistä suhdetta. Tarkastelemme asiakastyytyväisyyden ja markkinointitasojen välistä suhdetta.
Tärkeimmät havainnot
- Spearmanin järjestyskorrelaatioanalyysi soveltuu erityisesti ordinaalisille asteikoille.
- Excelin käyttö mahdollistaa nopean rangkorrelaation laskennan ja visualisoinnin.
- Heikko positiivinen yhteys markkinointitasojen ja asiakastyytyväisyyden välillä osoittaa, että enemmän sijoituksia markkinointiin eivät välttämättä johda korkeampaan tyytyväisyyteen.
Askel-askeleelta ohjeet
Aloita syöttämällä relevanteista tiedoista. Keskitämme huomiota asiakastyytyväisyyteen ja markkinointitasoihin. Nämä tiedot kerättiin tapaustutkimuksen yhteydessä.
Voit ensin kopioida tiedot alkuperäisestä aineistosta ja liittää ne uuteen työlehteen. Määritä sarakkeiden otsikot selkeästi. Saattaa olla hyödyllistä nimetä sarakkeet "asiakastyytyväisyys" ja "markkinointitaso".
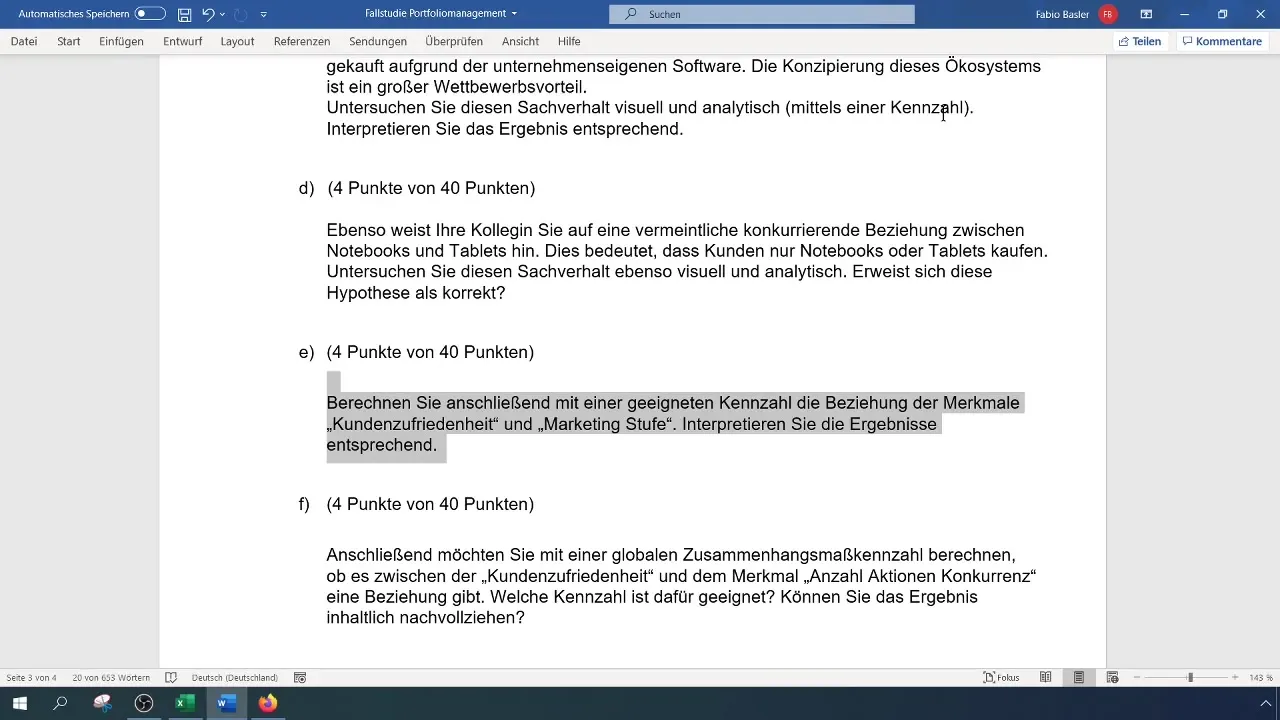
Kopioitujen tietojen jälkeen on tärkeää tarkistaa muuttujien asteikot. Asiakastyytyväisyys on ordinaalisesti asteikoitu, samoin markkinointitasot. Varmista, että ymmärrät tämän oikein välttääksesi virheitä myöhempiä laskelmia tehdessä.
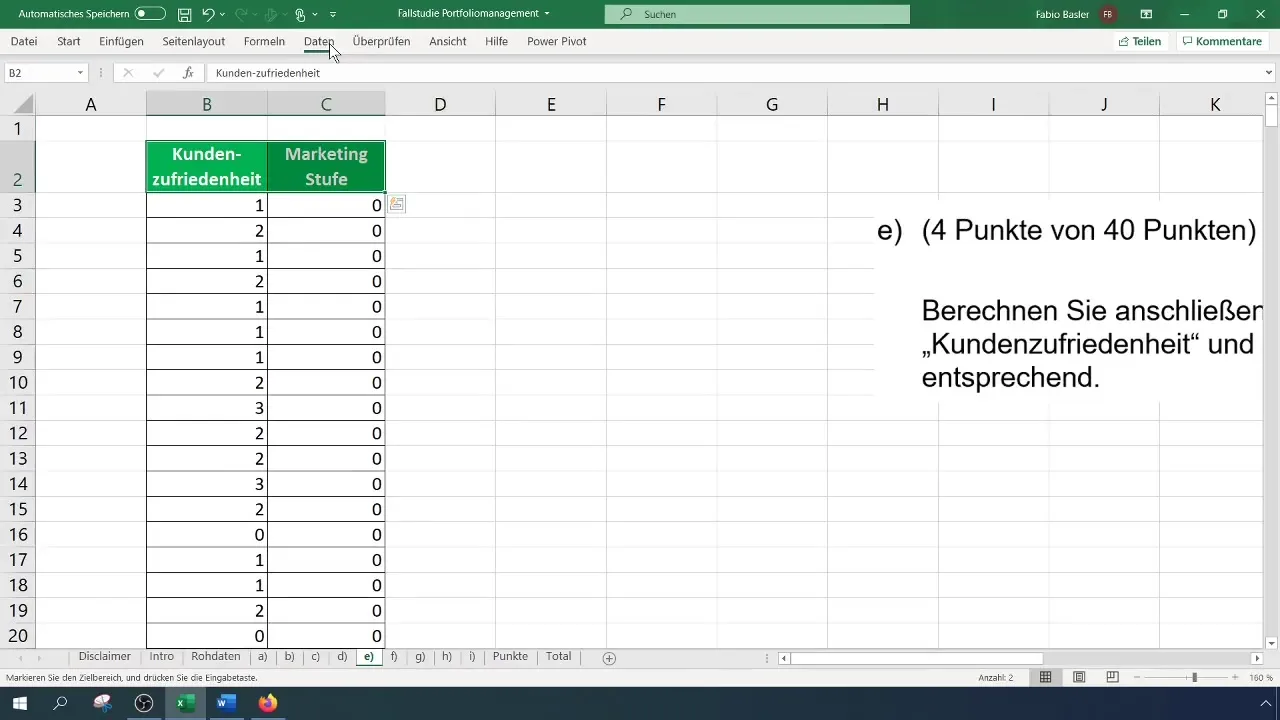
Seuraavaksi valmistele tietosi rangkorrelaatioanalyysiä varten. Tarvitset muuttujien rangit. Excelsior toimii tämän ansiosta "RANK.EQ" tai "RANK.AVG" -toiminnon kautta. Tämä toiminto antaa jokaiselle luvulle vastaavan asteen suhteessa määritettyyn matriisiin. Varmista, että työskentelet oikealla alueella.
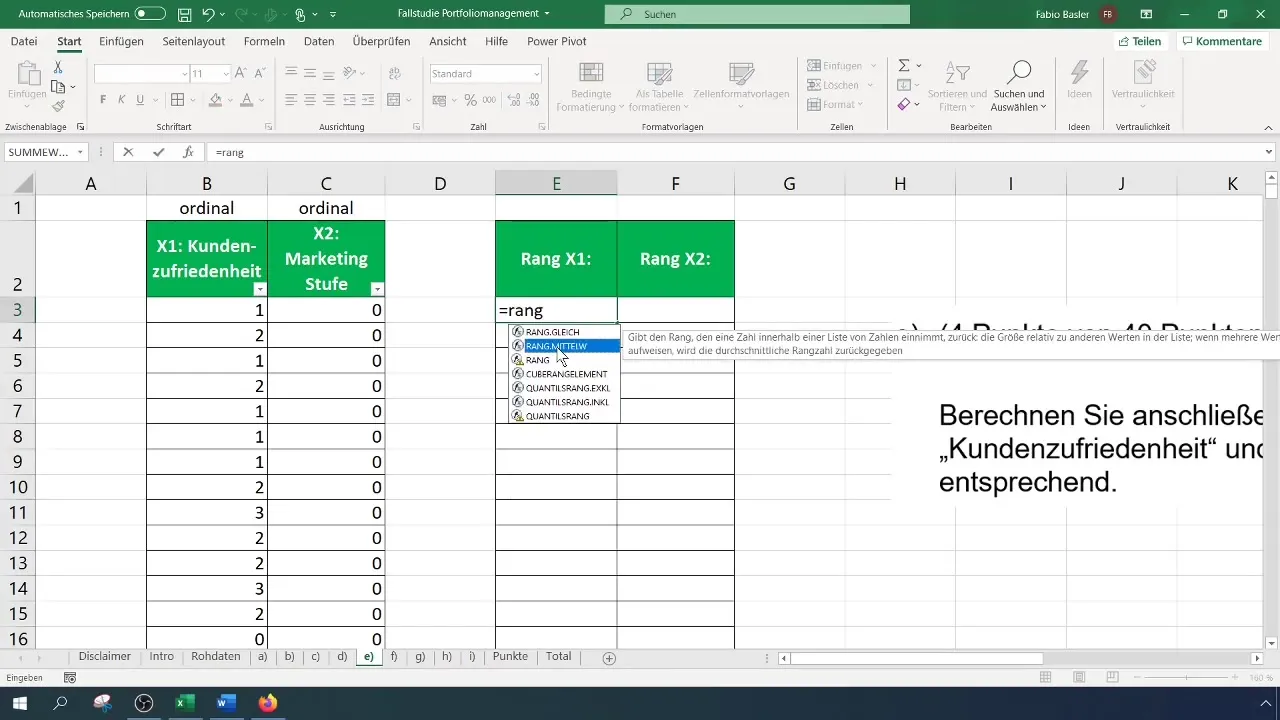
Kun haluat laskea rangit asiakastyytyväisyydelle, jonka merkitset tässä muuttujaksi X1, valitse ensin vastaava solu. Ensimmäistä havaintoa varten tämä tarkoittaa asiakastyytyväisyyden solun merkitsemistä ja sen jälkeen matriisin valitsemista, jossa rangit määritetään. On tärkeää, että pysyttelet koko matriisin suhteessa, jotta viittaus ei muutu, kun vedät kaavan alaspäin.
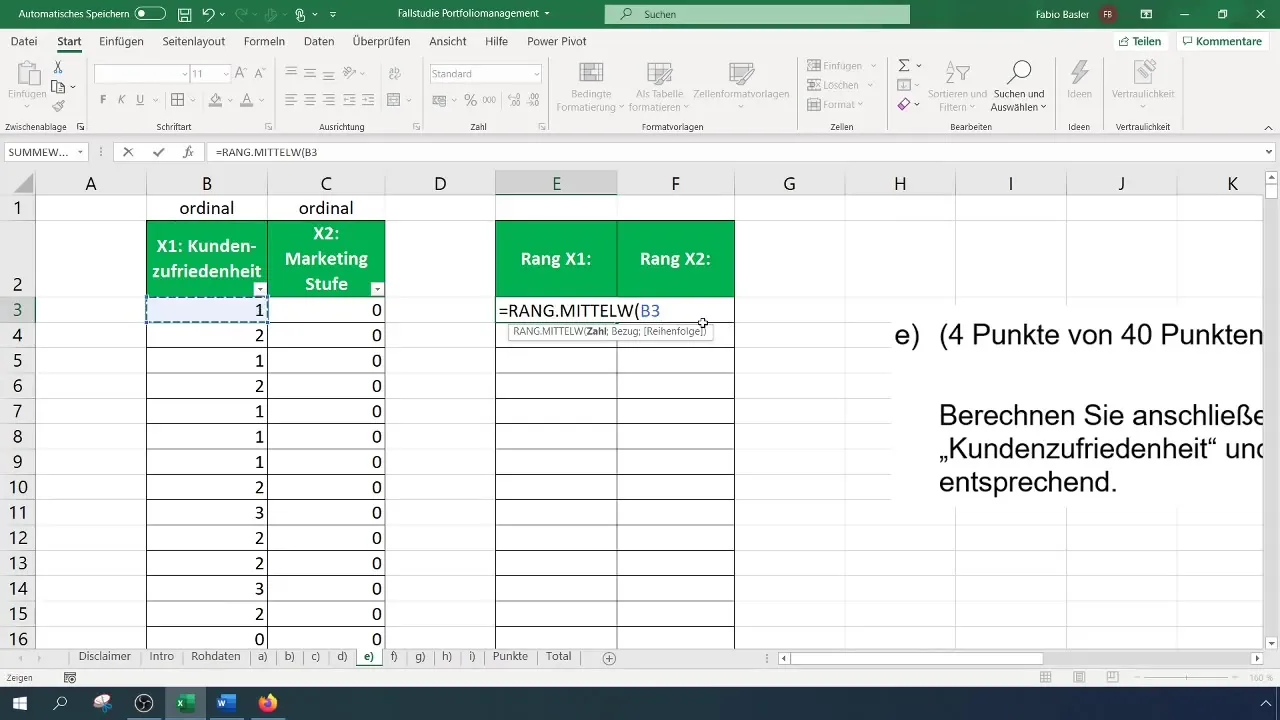
Aloita laskennan tekeminen kirjoittamalla kaava ja lisäämällä sitten tarvittavat parametrit. Noudata funktion oikeaa järjestystä. Määritä viittaus tietomatriisiisi ja valitse haluamasi järjestys, eli nouseva tai laskeva.
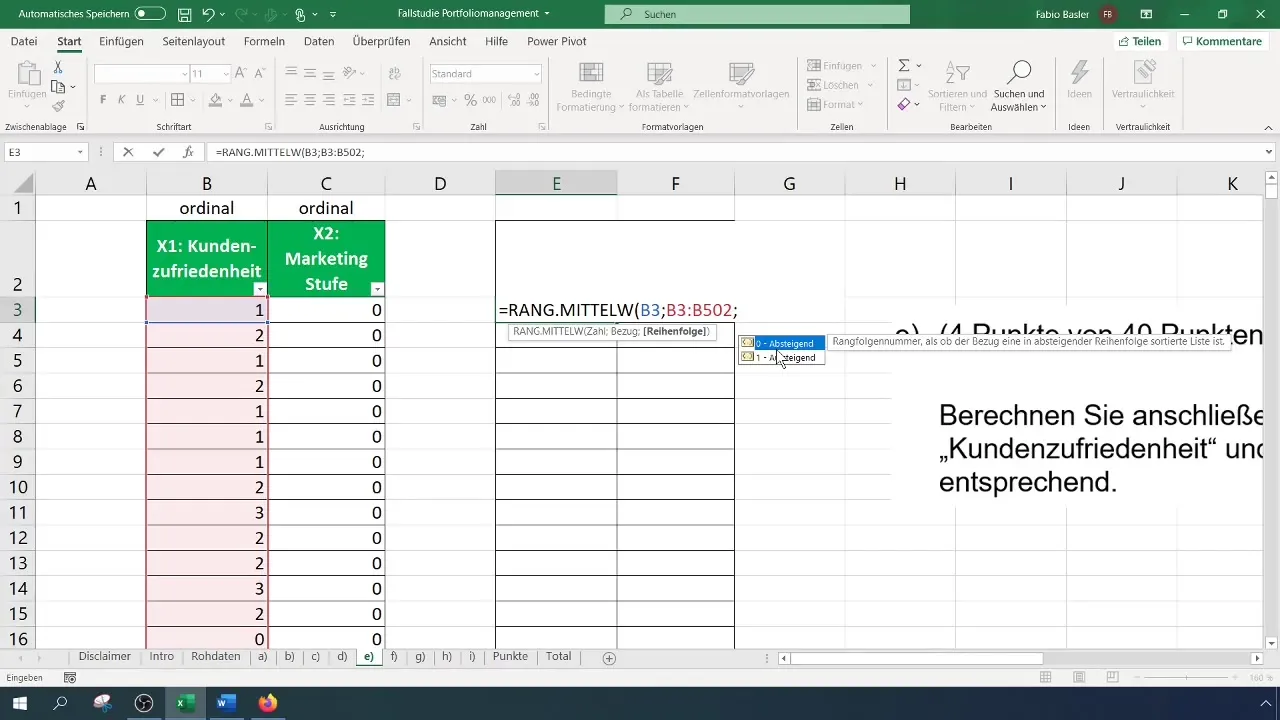
Kun haluat laskea rangit markkinointitasolle (X2), toista sama prosessi. Myös tässä on tärkeää pysyä koko tietoalueessa, jotta kaava toimii oikein, kun kopioit sen alaspäin. Nämä vaiheet takaavat, että rangit kullekin muuttujalle määritellään asianmukaisesti.
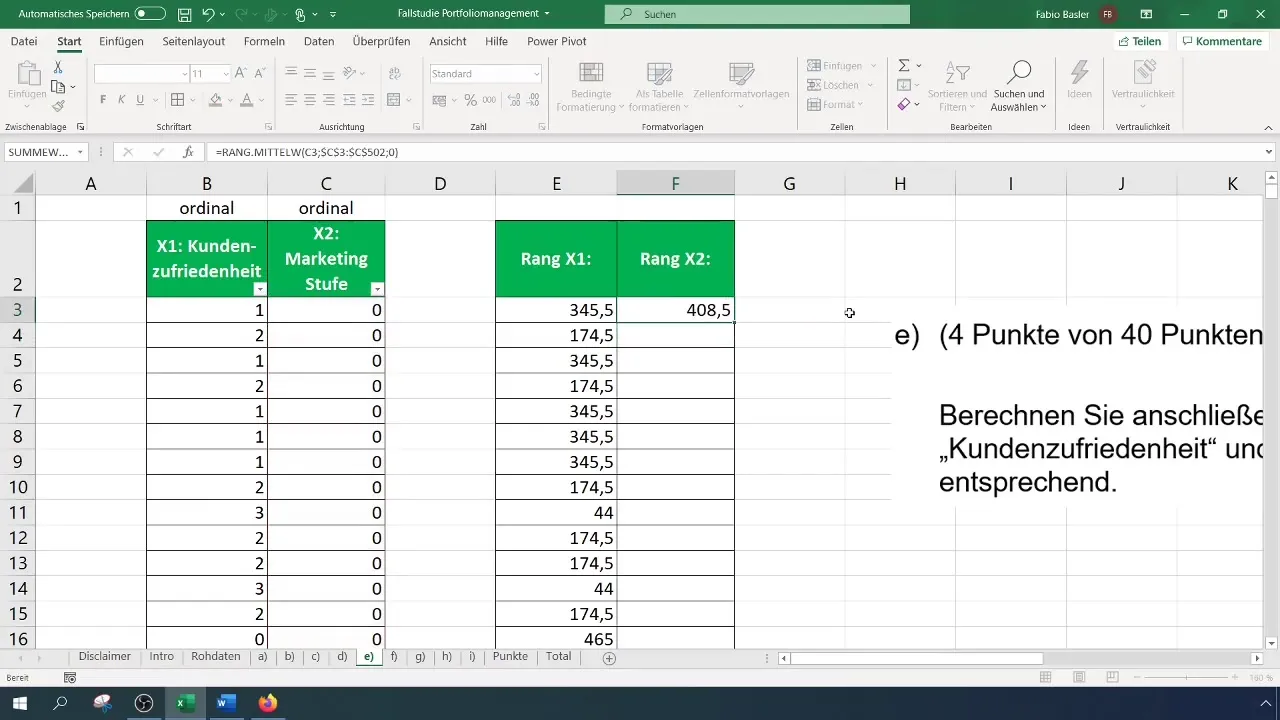
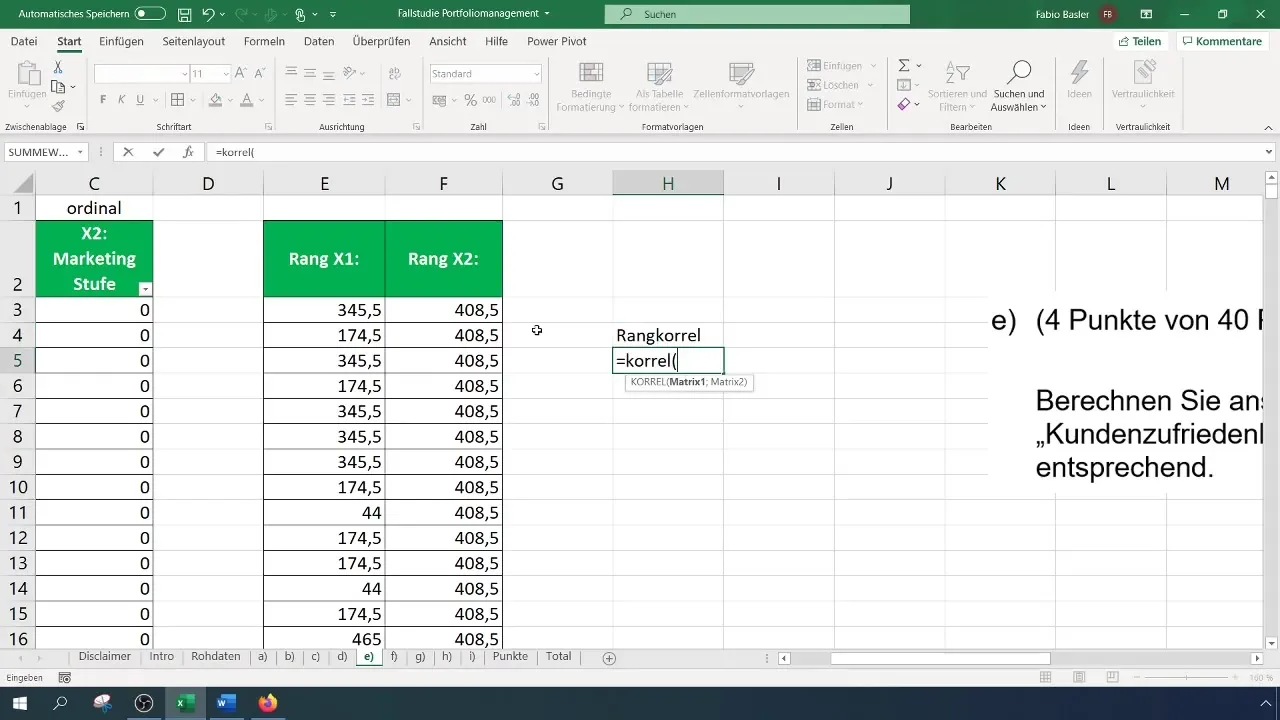
Kun olet saanut rangit molemmille muuttujille, voit laskea rangkorrelaation. Käytä "CORREL" -toimintoa. Tämä funktio mahdollistaa X1:n ja X2:n rangit valitsemisen ja korrelaation laskemisen. Tulos antaa sinulle yhteyden voimakkuuden näiden kahden muuttujan välillä.
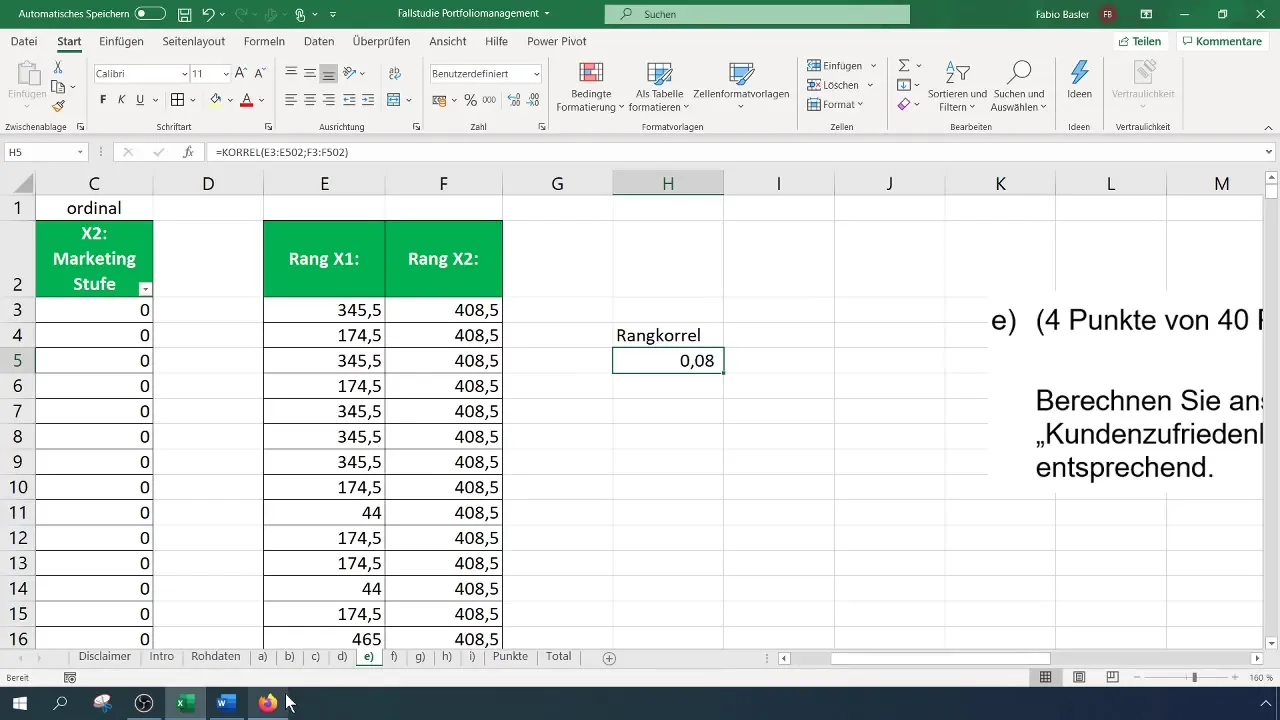
Omissa tuloksissasi korrelaatio on 0,082, mikä viittaa heikkoon myönteiseen yhteyteen. Tämä luku osoittaa, että vaikka suuntaus parempaan asiakastyytyväisyyteen lisääntyneiden markkinointikulujen kanssa on olemassa, tämä yhteys ei ole vahva.
Lopuksi sinun tulisi dokumentoida tulosten tulkinta. Taulukko voi auttaa sinua havainnollistamaan, missä rangkorrelaatio sijaitsee, ja selventämään kahden muuttujan välistä suhdetta.
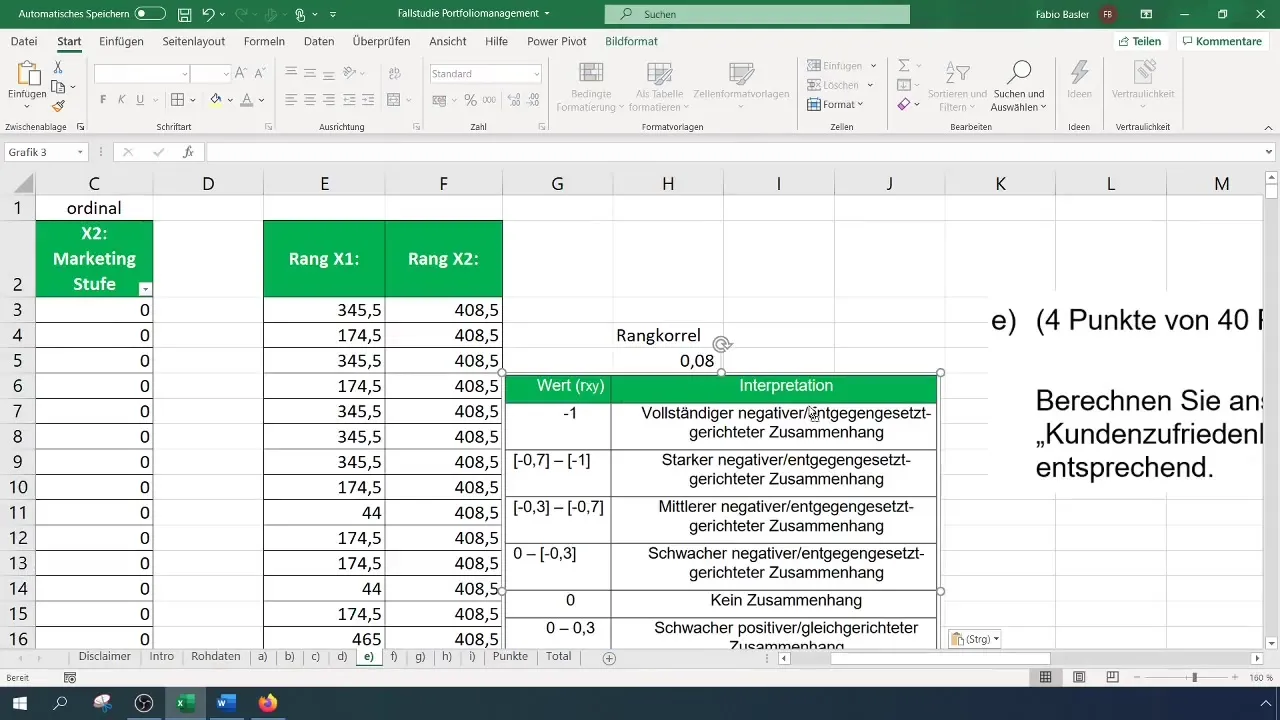
Rangkorrelaatioanalyysin lähestymistapa auttaa saamaan laadullisia näkemyksiä kvantitatiivisista tiedoista ja osoittaa, miten markkinointikulut saattavat vaihdella ilman että suoraan asiakkaiden tyytyväisyyttä lisättäisiin.
Yhteenveto
Tässä oppaassa opit suorittamaan rangkorrelaatioanalyysin Excelissä. Ensin olet valmistanut tiedot oikein ja sitten määrittänyt molempien muuttujien rangit. Lopuksi olet laskenut rangkorrelaation, jotta voit kvantifioida markkinointiluokan ja asiakastyytyväisyyden välisen yhteyden.
Usein kysytyt kysymykset
Kuinka erilaisia ovat Spearman ja Kendall?Spearman ja Kendall ovat molemmat rangkorrelaatiokertoimia, jotka lasketaan kuitenkin eri tavalla. Spearman perustuu rangierojen määrään, kun taas Kendall käyttää vastausten ja ei-vastausten määrää.
Kuinka valitsen sopivan korrelaation?Korrelaation valitseminen riippuu tietojen tyypistä. Ordinaalisesti asteikoiduille tiedoille Spearman sopii, metrisille tiedoille usein käytetään Pearsonia.
Vaihtaisinko regression korrelaation sijaan?Kyllä, regressio voi olla hyödyllinen yhden tai useamman riippumattoman muuttujan vaikutuksen tutkimisessa riippuvalla muuttujalla, korrelaatio osoittaa vain suhteen.


