Onnistunut odotusarvon 1-SP-testi Excelissä

Tilastolliset testit ovat keskeinen osa tietojen analysointia ja päätöksentekoa. Erityisesti biotekniikan alalla voi olla ratkaisevaa testata hypoteeseja vaikuttavien aineiden onnistumisprosentista. Tässä opetusohjelmassa opit, miten Excelissä suoritetaan tehokkaasti yhden otoksen testi (1-SP-testi ) odotusarvolle, jonka varianssi tunnetaan.

Keskeiset havainnot

Tämä opas opettaa sinulle:

• 1-SP-testin teoreettisen perustan.
• Vaiheet testin suorittamiseksi Excelissä.
• Tulosten tulkinnan.

Tietojen valmistelu

Jotta voit suorittaa 1-SP-testin Excelissä, tarvitset ensin tarvittavat tiedot. Esimerkissämme oletamme tilanteen, jossa analysoidaan tehoaineiden onnistumisprosenttia. Tiedetään, että keskimääräinen onnistumisprosentti on ollut 59 %, ja sen keskihajonta on 19. Ensin sinun on syötettävä tietosi Excel-taulukkoon.

Varmista, että tiedot on järjestetty sarakkeisiin, jotta voit käyttää niitä myöhemmin. Selkeä yleiskuva auttaa sinua ymmärtämään yksittäisiä vaiheita helpommin.

Testin yleiskatsaus

1-SP-testillä tarkistetaan, poikkeaako keskimääräinen onnistumisarvo merkittävästi määritellystä arvosta. Tässä tapauksessa tarkistetaan, voidaanko 59 prosentin onnistumisastetta nostaa merkittävästi tulevaisuudessa.

Muodostetaan hypoteesit

Testiä varten muotoilemasi hypoteesit ovat ratkaisevan tärkeitä:

• Nollahypoteesi (H0): Todellinen odotusarvo on yhtä suuri kuin 59 (σ = 59 %).
• Vaihtoehtoinen hypoteesi (H1): Todellinen odotusarvo on suurempi kuin 59 %.

Hypoteeseja muotoiltaessa olisi keskityttävä siihen, mitä tarkalleen ottaen on testattava ja miten tämä ilmenee kontekstissasi.

On tärkeää tunnistaa selvästi nollahypoteesin ja vaihtoehtoisen hypoteesin välinen ero, sillä ne muodostavat perustan seuraaville laskelmille.

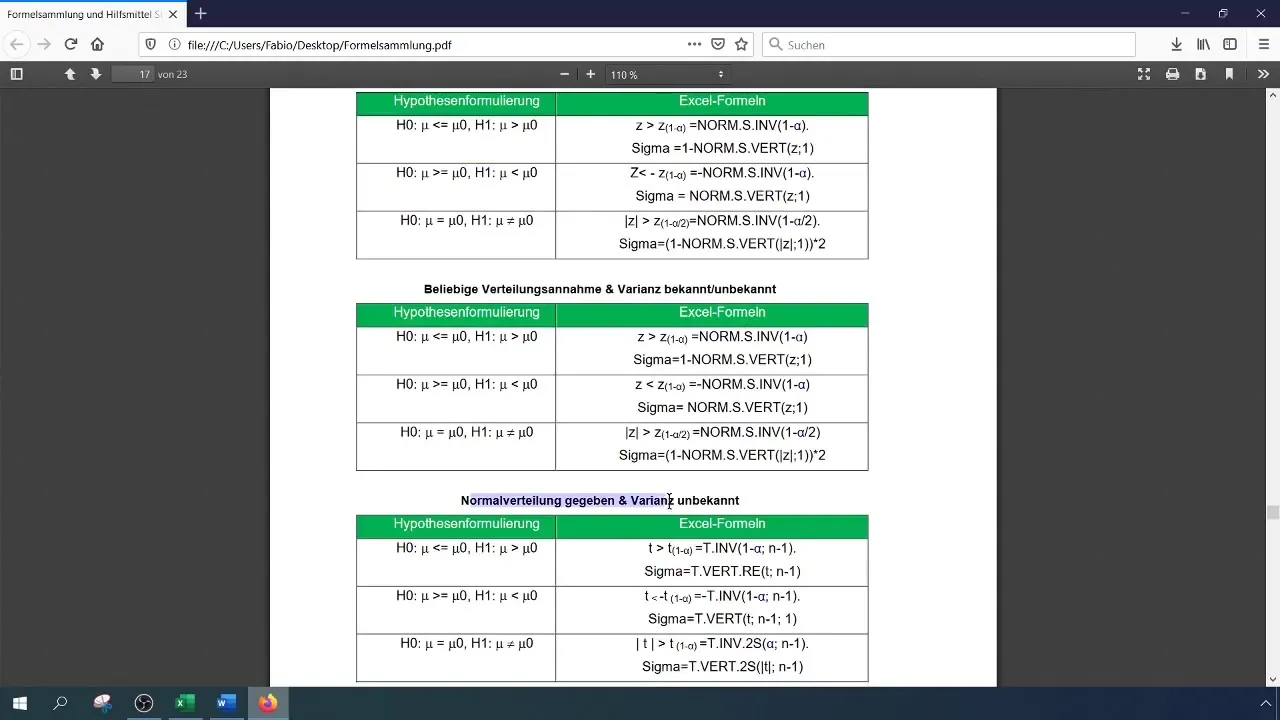
Otoksen kerääminen

Testiämme varten otamme 500 vaikuttavan aineen näytteen. On tärkeää huomata, että otoksen valinta on edustava, ja sen pitäisi taata asianmukaisen menetelmän avulla, että tulokset voidaan realistisesti siirtää koko perusjoukkoon.

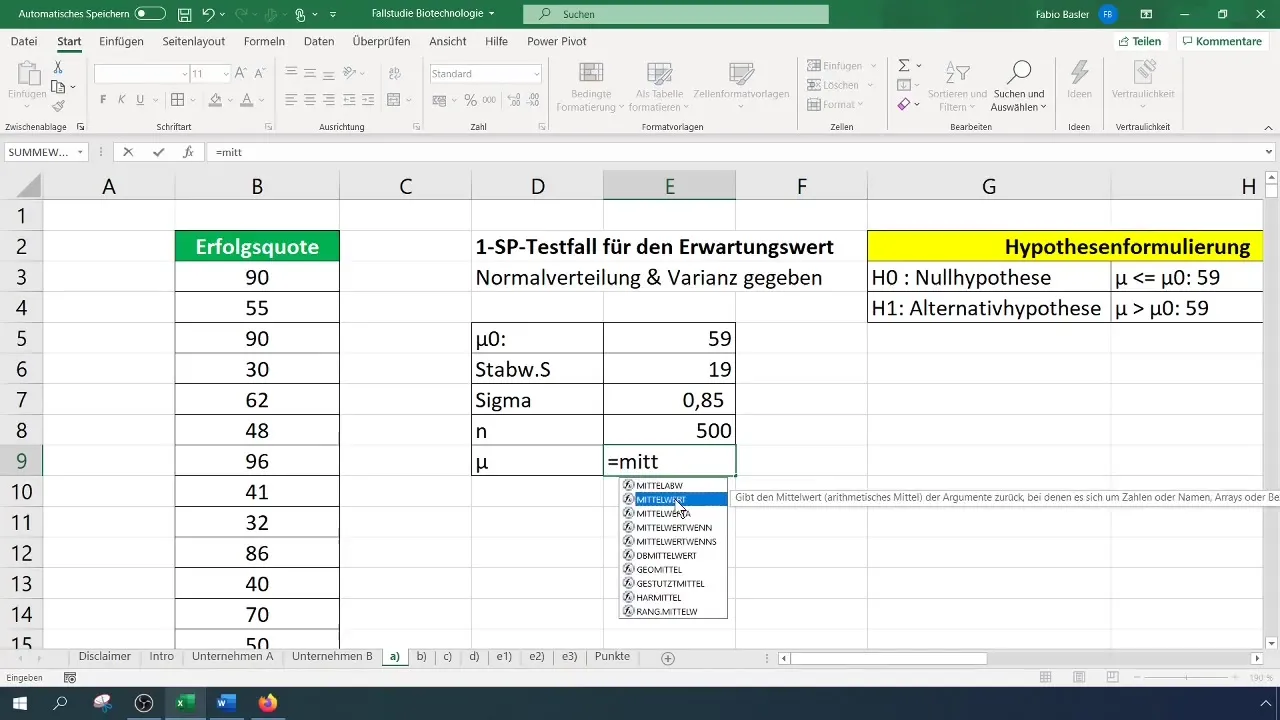
Testiä varten lasketaan ensin aritmeettinen keskiarvo. Tämän pitäisi olla helppo tehdä käyttämällä sopivaa kaavaa Excelissä.

Testimuuttujan laskeminen

Testimuuttuja 1-SP-testiä varten määritetään seuraavan kaavan avulla.

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]

Tässä (\bar{x}) tarkoittaa otoksen keskiarvoa, (\mu_0) oletettua keskiarvoa (tässä tapauksessa 59), (\sigma) keskihajontaa (tässä tapauksessa 19) ja (n) otosten lukumäärää (500).

Kun olet lisännyt arvot kaavaan, laske testistatistiikka määrittääksesi, onko se merkitsevä vai ei.

Kriittisen arvon määrittäminen

Jos merkitsevyystaso on 1 % (0,01), sinun on luettava tai laskettava kriittinen arvo. Voit tehdä tämän Excelissä NORM.S.INV-funktiolla.

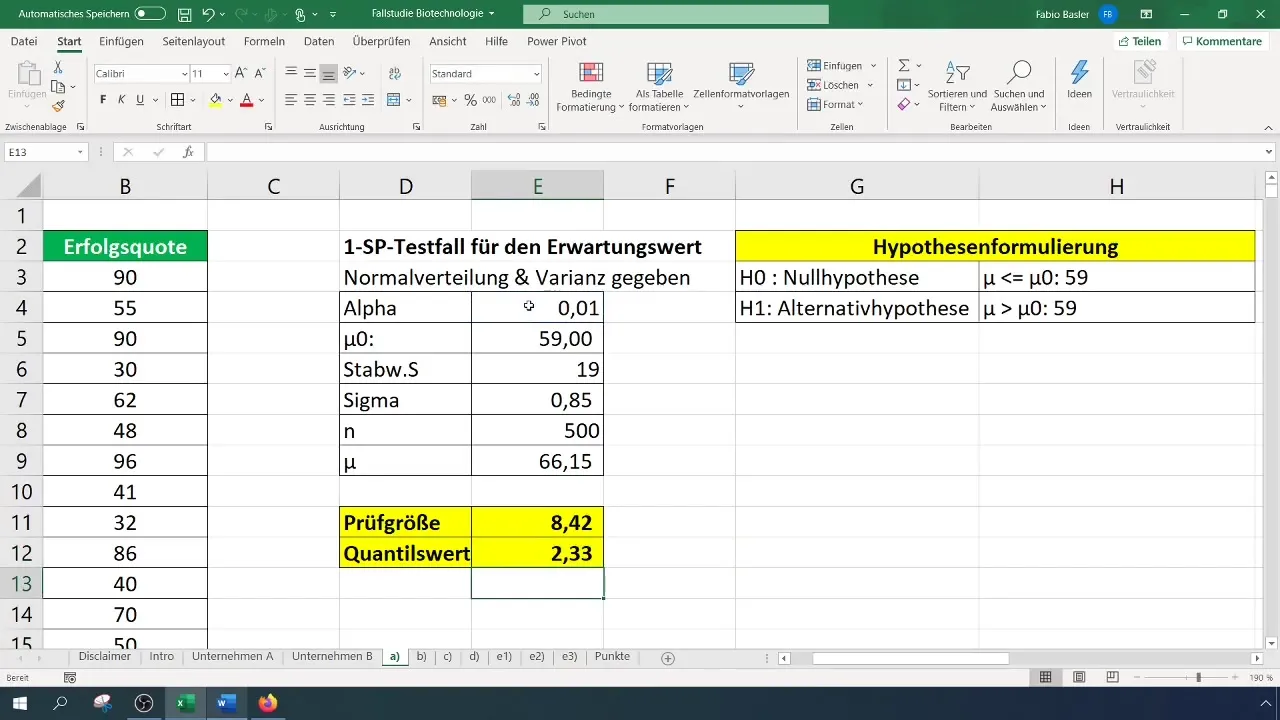
Kaava on seuraava:

[ \text{NORM.S.INV}(1 - \alpha)] ]

Jossa (\alpha) on merkitsevyystaso (0,01). Määritettyä arvoa käytetään vertailuperusteena testimuuttujaan nähden.

Testin suorittaminen

Nyt kun sinulla on sekä testistatistiikka että kriittinen arvo, vertaa näitä kahta:

• Jos testitilasto on suurempi kuin kriittinen arvo, nollahypoteesi hylätään.
• Muussa tapauksessa nollahypoteesia ei voida hylätä.

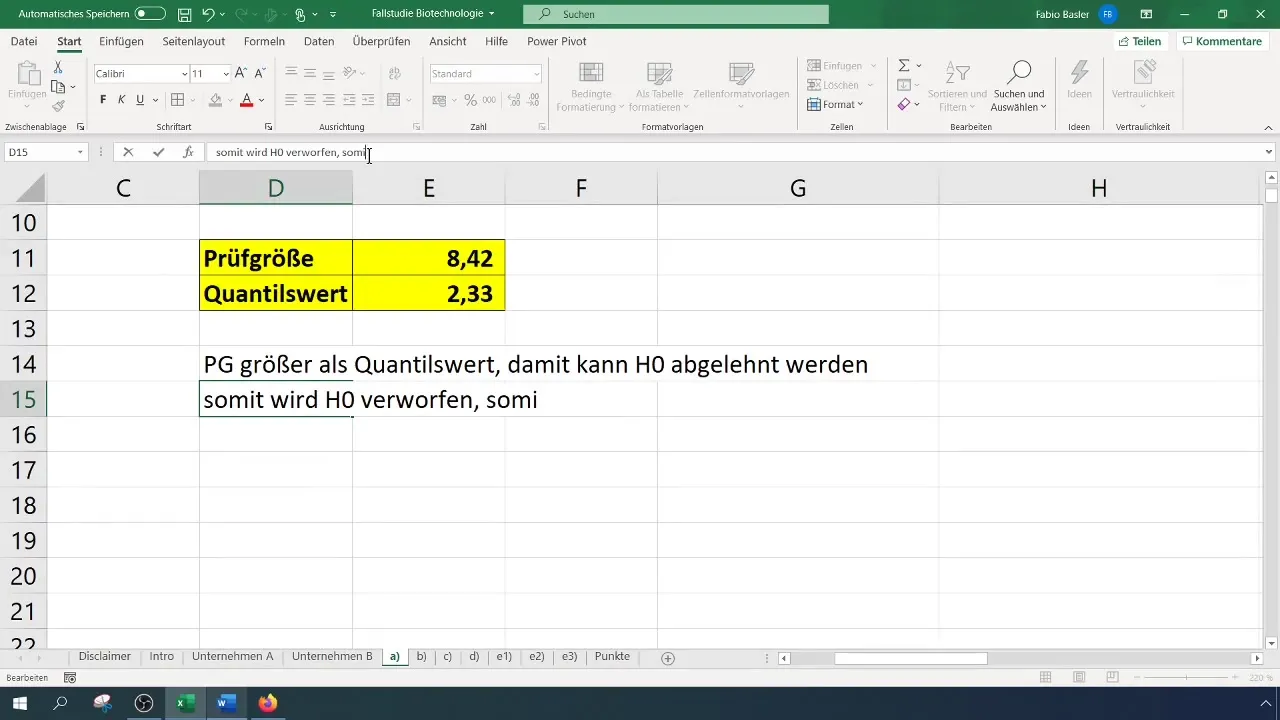
Tapauksessamme testitilastoksi saadaan 8,4, joka ylittää kriittisen arvon 2,33. Voimme siis hylätä nollahypoteesin. Tämä osoittaa, että onnistumisprosentti parani merkittävästi.

Tulosten tulkinta

Kun olet suorittanut testin ja saanut tulokset, sinun on tulkittava niitä selkeässä yhteydessä. Nollahypoteesin hylkääminen tarkoittaa, että uusi testattu arvo eroaa merkittävästi aiemmasta, tässä tapauksessa 59 %:sta.

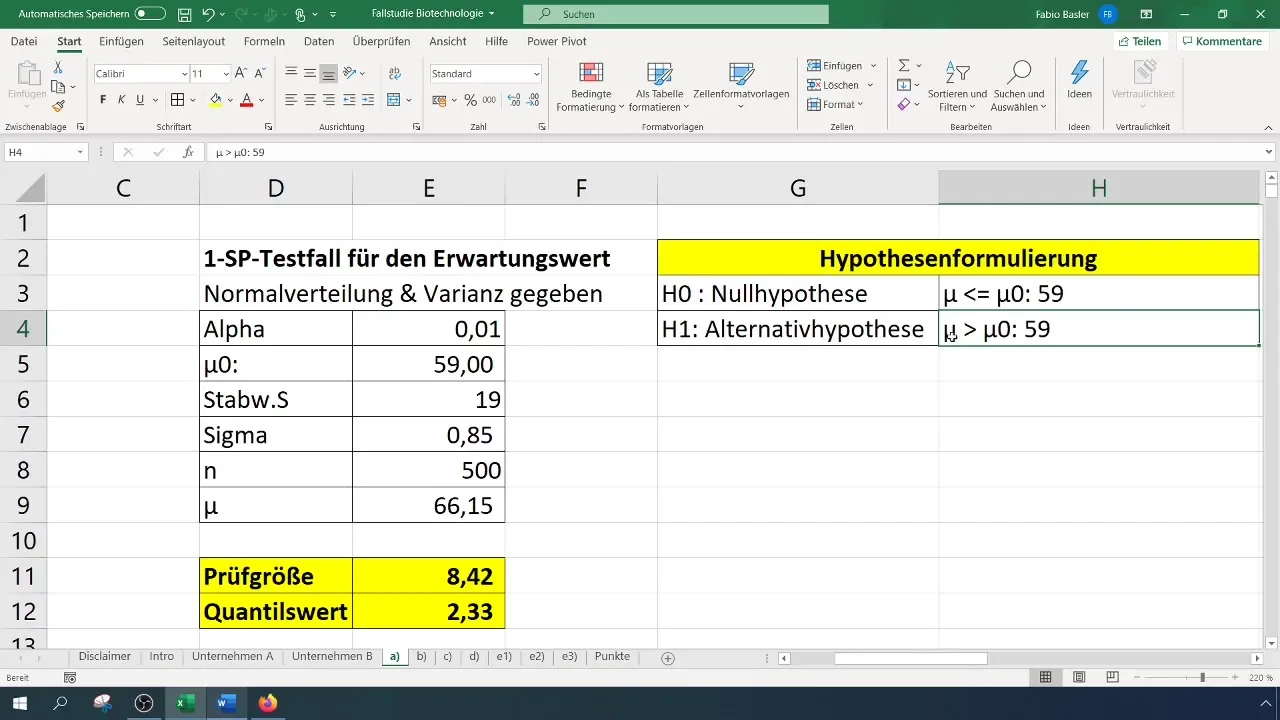
Tämä tieto on erittäin tärkeää organisaatiosi strategisen päätöksenteon kannalta. Se vahvistaa, että ponnistelut onnistumisasteen parantamiseksi olivat tehokkaita.

Yhteenveto

Tässä opetusohjelmassa opit, miten odotetun arvon 1-SP-testi suoritetaan Excelissä. Tapaustutkimuksen avulla pystyit seuraamaan vaiheita hypoteesien asettamisesta tietojen laskemiseen ja tulosten tulkintaan. Tämä tieto on arvokasta paitsi tieteellisissä analyyseissä myös käytännön sovelluksissa yrityksessä.