Kaksinäytteinen t-testi on olennainen työkalu tilastotieteessä, kun haluat tutkia eron kahden keskiarvon välillä. Tässä oppaassa opit, kuinka suoritat tämän testin helposti ja tehokkaasti Excelissä. Bioalan esimerkki auttaa sinua vertailemaan ja tilastollisesti analysoimaan kahden kilpailevan yrityksen onnistumisprosentteja.
Tärkeimmät havainnot
- Kaksinäytteisen t-testin soveltaminen kahden keskiarvon eron analysointiin.
- Oletusten muotoilu ja tarkistus.
- Excen käyttö tulosten laskemiseen ja esittämiseen.
Askel-askeleelta -opas
Aloitetaan luomalla tarvittavat tiedot ja suorittamalla testi Excelissä.
Askel 1: Valmistele tiedot
Aloita keräämällä raakadataa kahden yrityksen onnistumisprosenteista. Oletetaan, että sinulla on käytettävissäsi dataa yrityksestä A ja B. Sinulla on 100 näytettä kummastakin yrityksestä.

Askel 2: Näytenumero ja keskiarvot
Luo taulukko Exceliin, jossa vertaat näytteitä ja niiden keskiarvoja. Laske ensin näytemäärä (N) kummallekin yritykselle sekä keskiarvo (X).

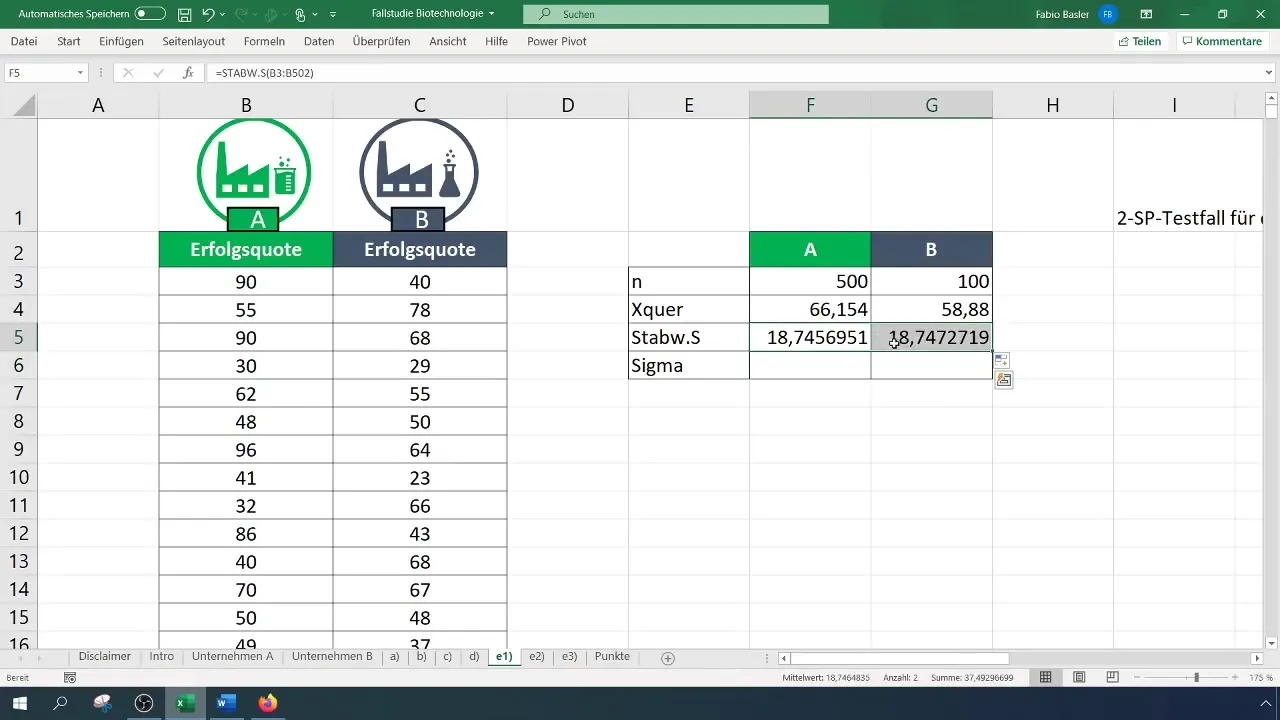
Askel 3: Laske standardipoikkeamat
Lasketaan standardipoikkeama kummallekin yritykselle. Nämä arvot ovat tärkeitä varianssin ja jatkotoimenpiteiden laskemisessa.
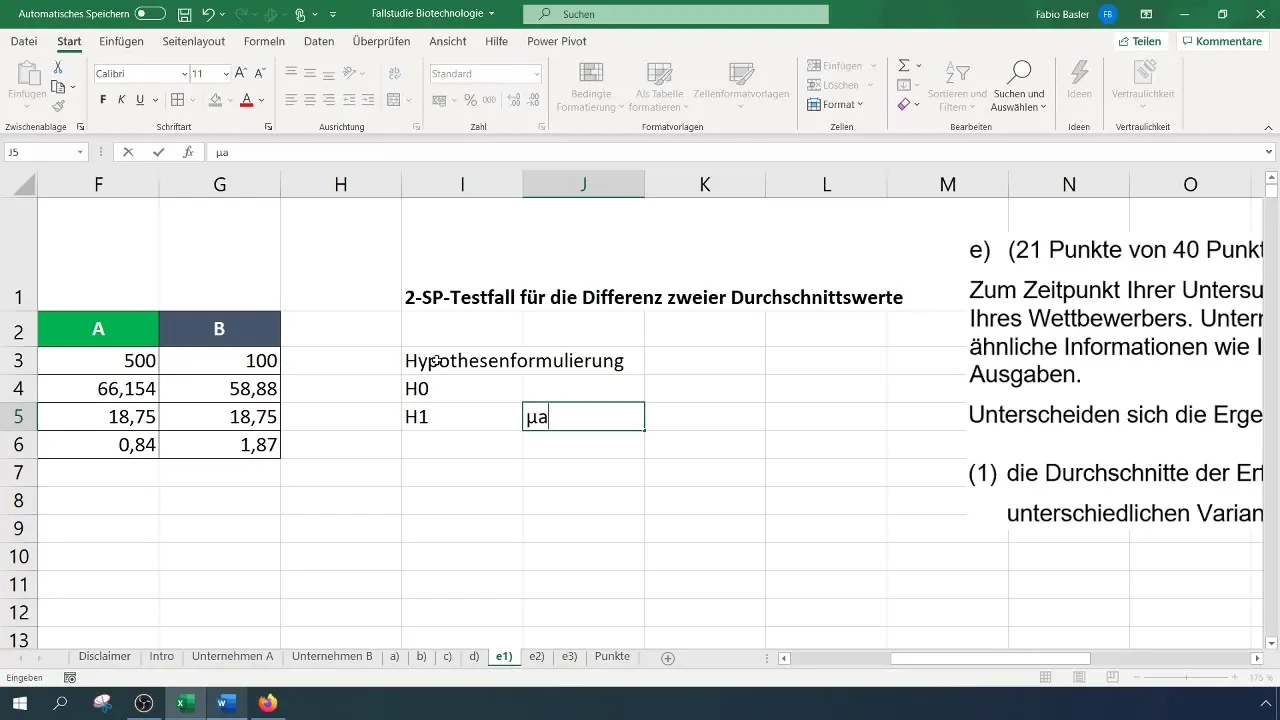
Askel 4: Muotoile hypoteesit
Laadi nollahypoteesi (H_0): Yritysten A ja B onnistumisprosenttien keskiarvot ovat samat. Vaihtoehtohypoteesi (H_1): Onnistumisprosenttien keskiarvot ovat erilaiset.
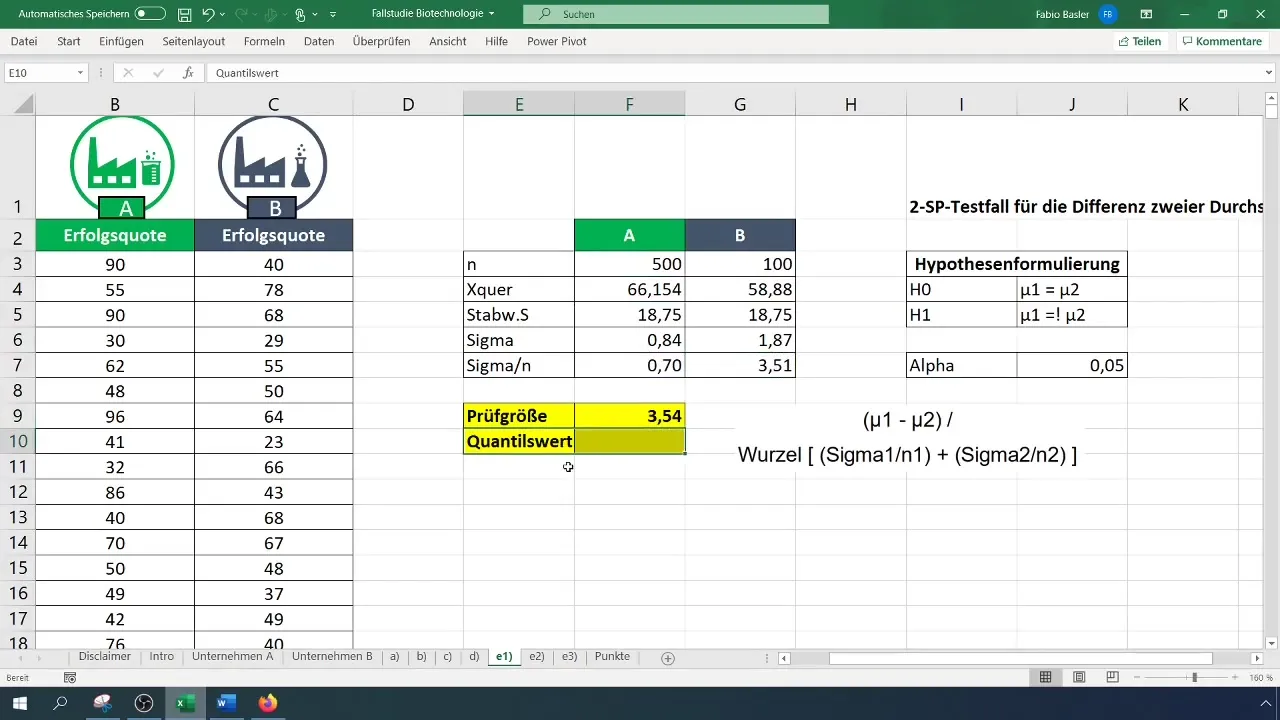
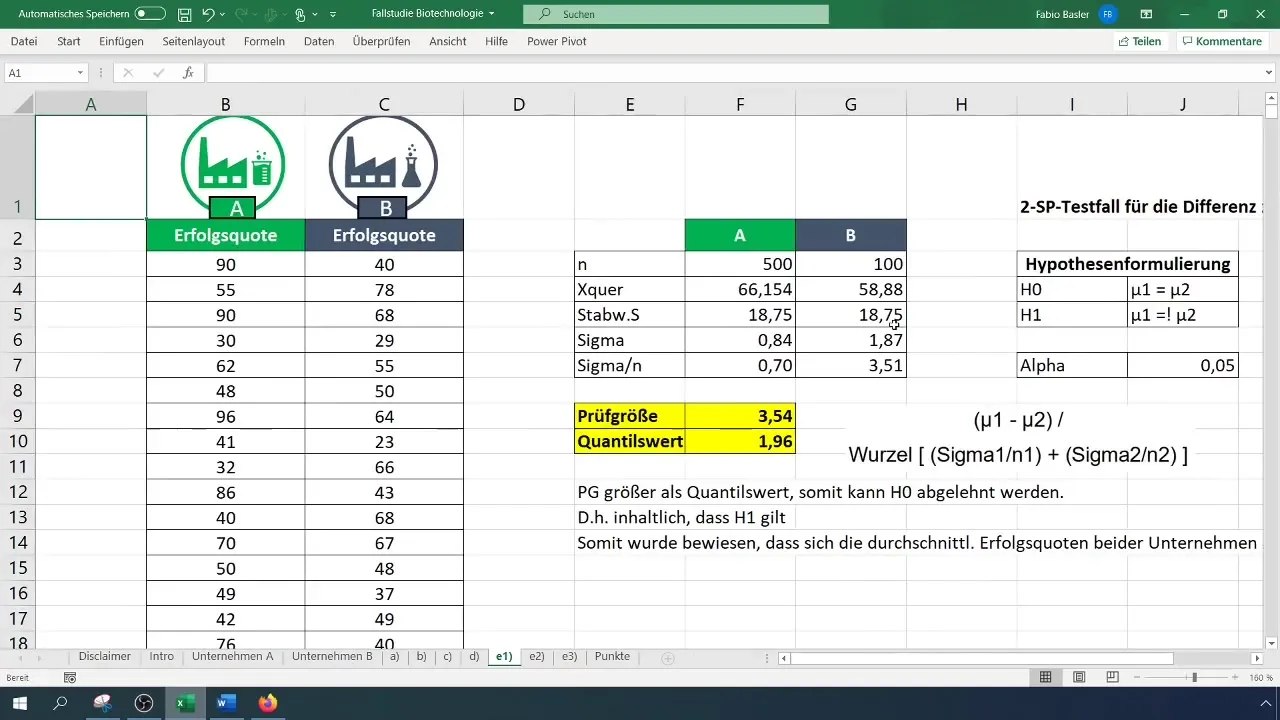
Askel 5: Laske testitilastosuure
Lasketaan testitilastosuure käyttäen t-testin kaavaa. Laske keskiarvojen erotus ja jaa se näytenumeroiden varianssien summan neliöjuurella.
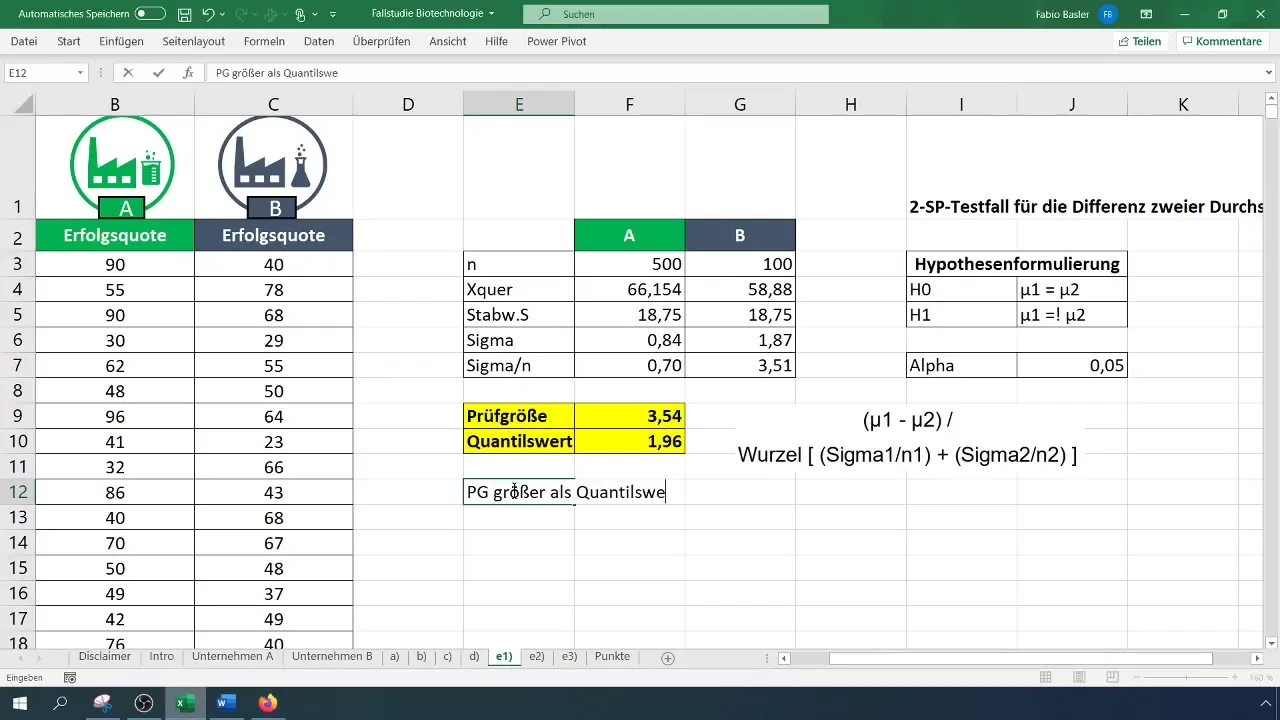
Askel 6: Määritä kriittinen arvo
Käytä kaksisuuntaista t-jakaumaa kriittisen arvon löytämiseen. Aseta alfa-taso 0,05:een. Tarkista t-jakaumataulukosta tai laske tekijä suoraan Excelissä.
Askel 7: Tee päätös hypoteesista
Vertaa laskettua testitilastosuuretta kriittiseen arvoon. Jos testitilastosuure on suurempi kuin kriittinen arvo, hylkää nollahypoteesi (H_0) ja vahvista siten vaihtoehtohypoteesi (H_1).
Askel 8: Tulosten tulkinta
Lopuksi tulkitse tulos. Tässä esimerkissä havaittiin keskimääräisten onnistumisprosenttien kahden yrityksen välillä olevan merkittävä ero.
Yhteenveto
Olet oppinut suorittamaan kaksinäytteisen t-testin Excelissä voidaksesi tutkia kahden ryhmän keskiarvojen eroja. Dataan valmistautumisesta hypothesioiden muotoiluun ja tulosten tulkintaan tehdyt askeleet ovat ratkaisevia pätevien ja informoitujen päätösten tekemisessä.
Usein kysytyt kysymykset
Mikä on kaksinäytteinen t-testi?Kaksinäytteinen t-testi vertailee kahden ryhmän keskiarvoja selvittääkseen ovatko ne merkitsevästi erilaisia.
Miten muotoilen hypoteesit?Nollahypoteesi (H_0) olettaa, että keskiarvot ovat samat, kun taas vaihtoehtohypoteesi (H_1) olettaa ne olevan erilaiset.
Miten lasken testitilastosuureen?Testitilastosuure lasketaan keskiarvojen erotuksen ja näytenumeroiden varianssin summan neliöjuuren avulla.
Mitä teen laskennan jälkeen?Vertaa testitilastosuuretta kriittiseen arvoon päättääksesi voitko hylätä nollahypoteesin.
Miksi standardipoikkeama on tärkeä?Standardipoikkeama auttaa ymmärtämään dataan liittyvää muuttujaisuutta, mikä on tärkeää testitilastosuureen laskennassa.


