Tilastolliset testit ovat olennainen osa datan analysointia, erityisesti kun on kyse ryhmien välisistä erojen selvittämisestä. Eräs luotettava menetelmä, jota usein käytetään tutkimuksessa ja liike-elämässä, on Kahden otoksen F-testi. Tämä opas näyttää sinulle vaihe vaiheelta, miten voit toteuttaa tällaisen testin Excelissä ja vertailla kahden lääkeyrityksen muuttujia niiden tutkimuskuluihin liittyen.
Tärkeimmät havainnot
- Opit, miten voit vertailla kahden ryhmän variansseja F-testin avulla.
- Opas sisältää yksityiskohtaiset ohjeet testin suorittamiseen Excelissä, mukaan lukien Data-analyysi -toiminnon käyttö.
- Lopuksi tiedät, miten tulokset tulisi tulkita ja minkälaisia johtopäätöksiä niistä voidaan vetää.
Vaiheittainen opas
Vaihe 1: Datan valmistelu
Tarvitset ensin molempien yritysten tutkimuskulujen raakadatan. Avaa Excel-tiedosto ja kopioi kunkin yrityksen tutkimustiedot erillisille sarakkeille.

Vaihe 2: Otoskoon ja varianssin laskeminen
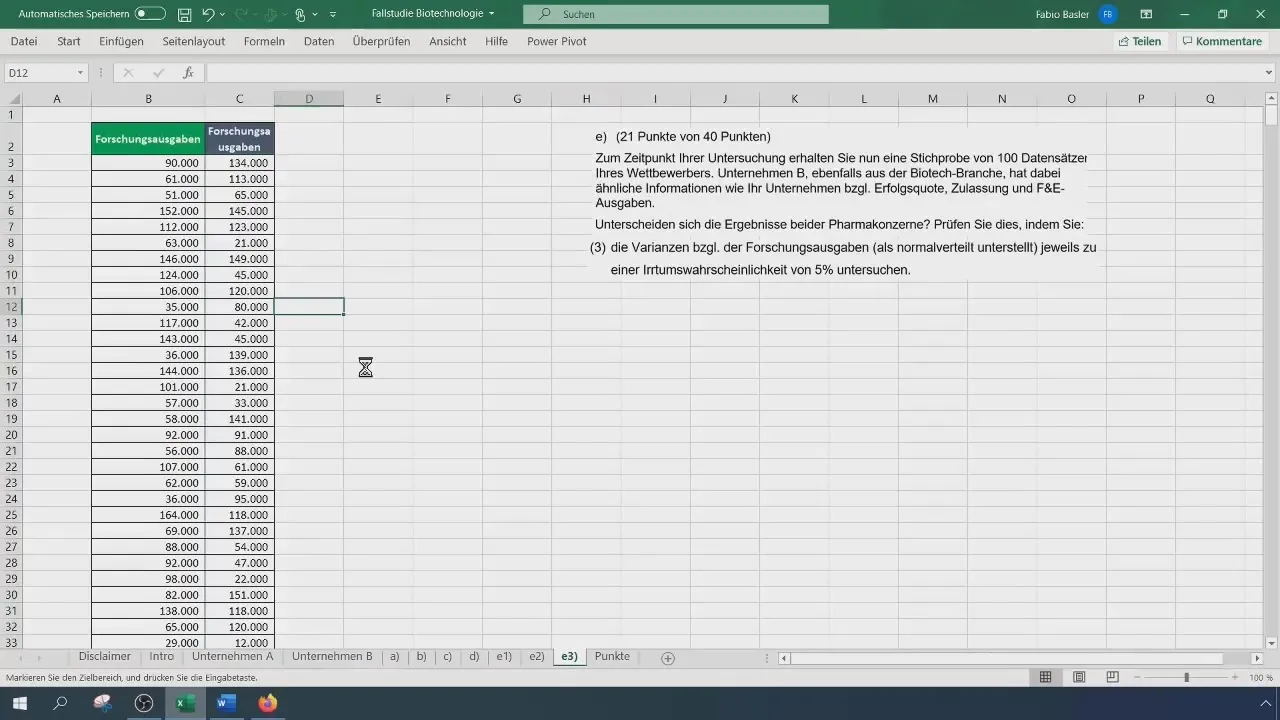
Otoskoko pysyy samana molempien yritysten kohdalla, 500 yritykselle A ja 100 yritykselle B. Jotta voit laskea datan varianssin, käytä VAR.S() -funktiota estimoidaksesi ryhmien varianssit. Varmista, että syötät arvot Excel-muodossa tarkkojen tulosten saamiseksi.
Vaihe 3: Hypoteesien muotoilu
F-testiä varten hypoteesit tulee määritellä seuraavasti:
- Nollahypoteesi (H0): σ1² = σ2² (Molempien yritysten varianssit ovat samat).
- Vaihtoehtohypoteesi (H1): σ1² ≠ σ2² (Molempien yritysten varianssit ovat erilaiset).
Vaihe 4: Testisuureen laskeminen
Lasketaan testisuure (F-tilastollinen tunnusluku) jakamalla molempien varianssien suhde. Käytä kaavaa Varianssi_A / Varianssi_B. Kun olet syöttänyt varianssit asianmukaisesti, saat vertailtavan F-tilastollisen tuloksen.
Vaihe 5: Kriittisen arvon määrittäminen
Kriittisen F-arvon määrittämiseksi tarvitset alfan tason (yleensä 0,05) ja asteikot. Asteikot lasketaan seuraavasti: df1 = n1 - 1 ja df2 = n2 - 1. Määritä kriittinen arvo käyttäen F.INV() -funktiota.

Vaihe 6: Päätöksen tekeminen
Vertaa laskettua F-tilastollista tunnuslukua kriittiseen F-arvoon. Jos F-tilastollinen tunnusluku on suurempi kuin kriittinen arvo, hylkää nollahypoteesi, muussa tapauksessa älä. Tässä esimerkissä hylkäämisperuste on, että testisuureen on oltava pienempi kuin kvantiilinen arvo (F kriittinen).

Vaihe 7: Hyödynnä Excelin Data-analyysiä
Excel tarjoaa myös mahdollisuuden suorittaa F-testi Data-analyysi -toiminnon kautta. Siirry ”Data” -välilehteen ja valitse ”Data-analyysi”. Valitse ”Kahden otoksen F-testi”. Syötä kumpaakin muuttujaa vastaavat alueet ja valitse tarvittavat asetukset.
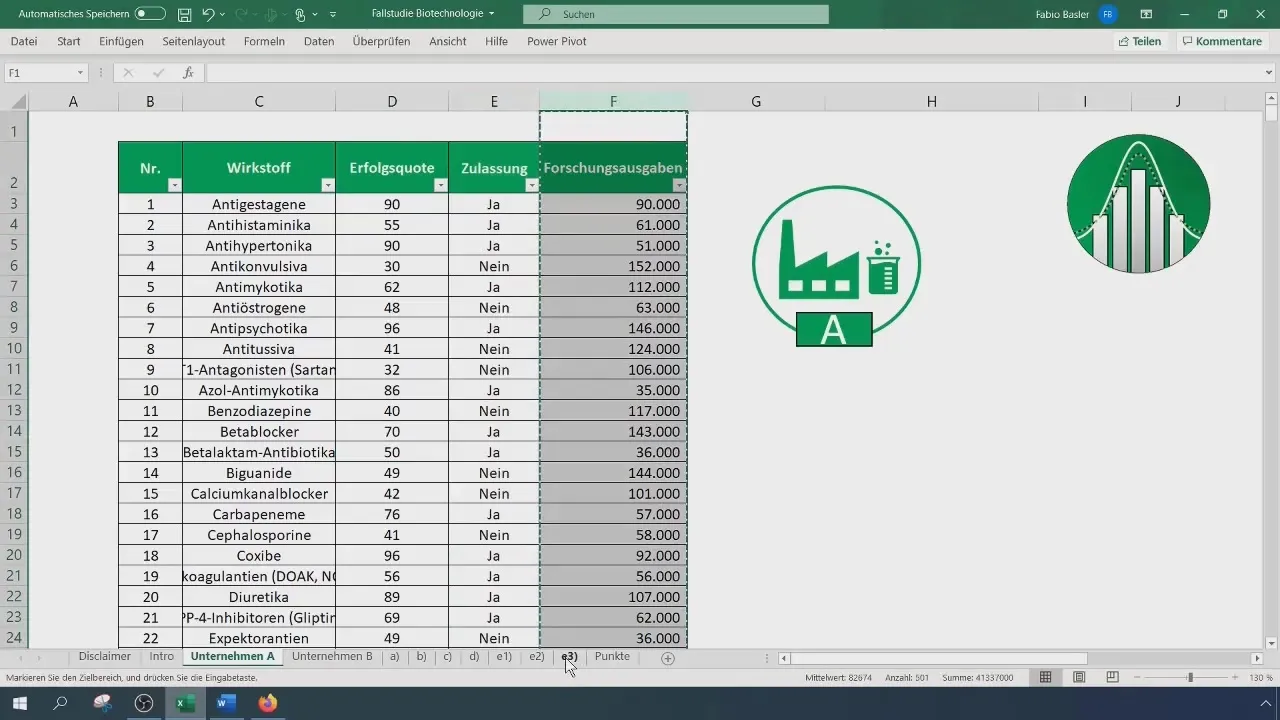
Vaihe 8: Tulosten tulkinta
Analysoi F-testin tulokset. Jos laskemasi F-tilastollinen tunnusluku ja p-arvo Excel-tulosteessa antavat samat tulokset kuin manuaalinen laskenta, voit päätellä, että molempien yritysten varianssit ovat samat.
Yhteenveto
Kahden otoksen F-testi on olennainen työkalu tilastollisessa analyysissä, joka mahdollistaa kahden ryhmän varianssien vertailun. Tässä oppaassa olet oppinut, miten suoritat tämän testin tehokkaasti Excelissä aina datan valmistelusta tulosten tulkintaan asti.
Usein kysytyt kysymykset
Mikä on Kahden otoksen F-testi?Kahden otoksen F-testi vertailee kahden ryhmän variansseja selvittääkseen, ovatko ne tilastollisesti merkittävästi erilaisia.
Milloin minun pitäisi käyttää F-testiä?F-testiä käytetään, kun haluat tarkistaa varianssien tasa-arvoisuutta kahden riippumattoman ryhmän välillä.
Miten lasken F-tilastollisen tunnusluvun?F-tilastollinen tunnusluku lasketaan jakamalla ensimmäisen ryhmän varianssi toisen ryhmän varianssilla.
Mitä teen, jos nollahypoteesi hylätään?Jos nollahypoteesi hylätään, voit olettaa, että kahden ryhmän varianssit ovat tilastollisesti merkittävästi erilaisia.
Onko olemassa vaihtoehtoja F-testille?Kyllä, voit käyttää myös Bartlettin testiä tai Levenen testiä, jos haluat testata varianssin homogeenisuutta.


