Tietojen analysointiin Excel-työkalujen avulla on ratkaisevan tärkeää liiketoiminnan ja myynnin menestykselle. Tässä oppaassa keskitytään korrelaatio- ja regressioanalyysiin, jotta voit selvittää, miten työntekijöiden määrä ja puheluiden määrä vaikuttavat liikevaihtoon. Näiden kahden analyysin suorittaminen auttaa sinua arvioimaan näitä suhteita kvantitatiivisesti ja tekee tulosten tulkinnan ymmärrettäväksi.
Tärkeimmät havainnot
- Ero korrelaation ja regressiion välillä: Korrelaatio näyttää kahden muuttujan välisen yhteyden, kun taas regressio tutkii useiden riippumattomien muuttujien vaikutusta yhteen riippuvaan muuttujaan.
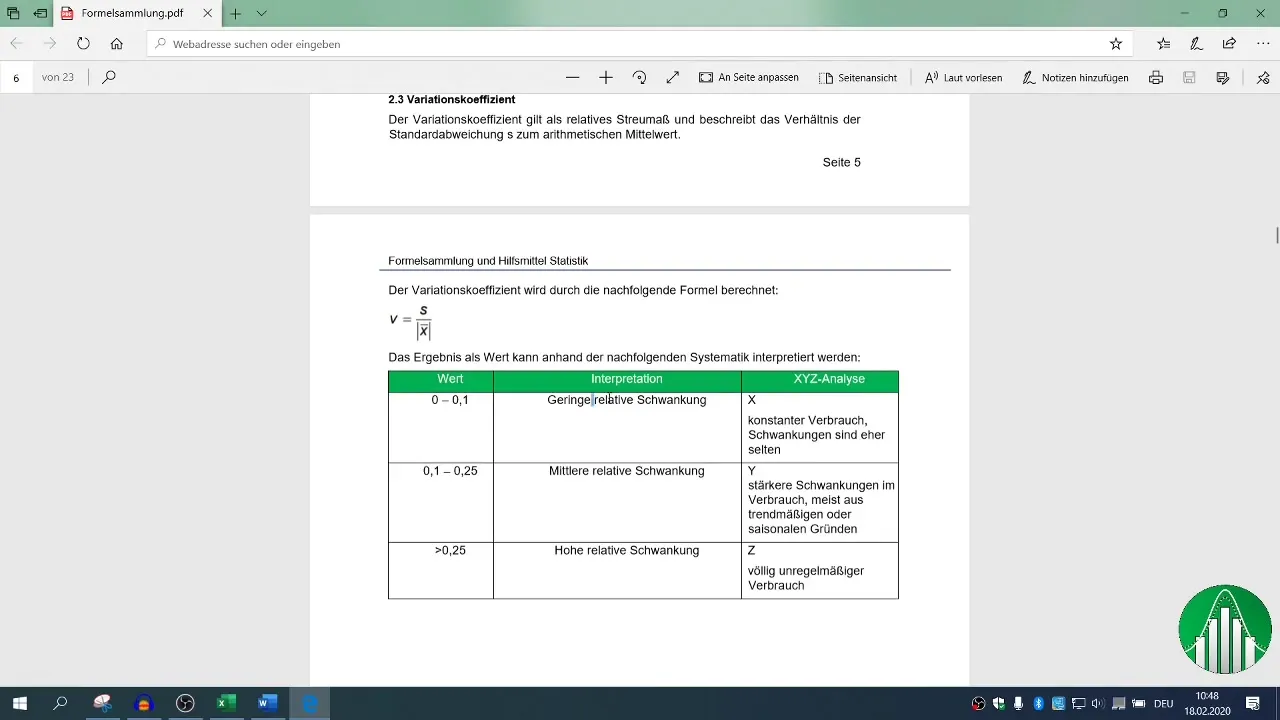
- Tietoa tilastollisesta merkitsevyydestä ja mallin laadusta.
- Riippujien tärkeyden kvantitatiivinen arviointi.
Vaiheittainen ohje
1. Valmistelut tietojen analysointia varten
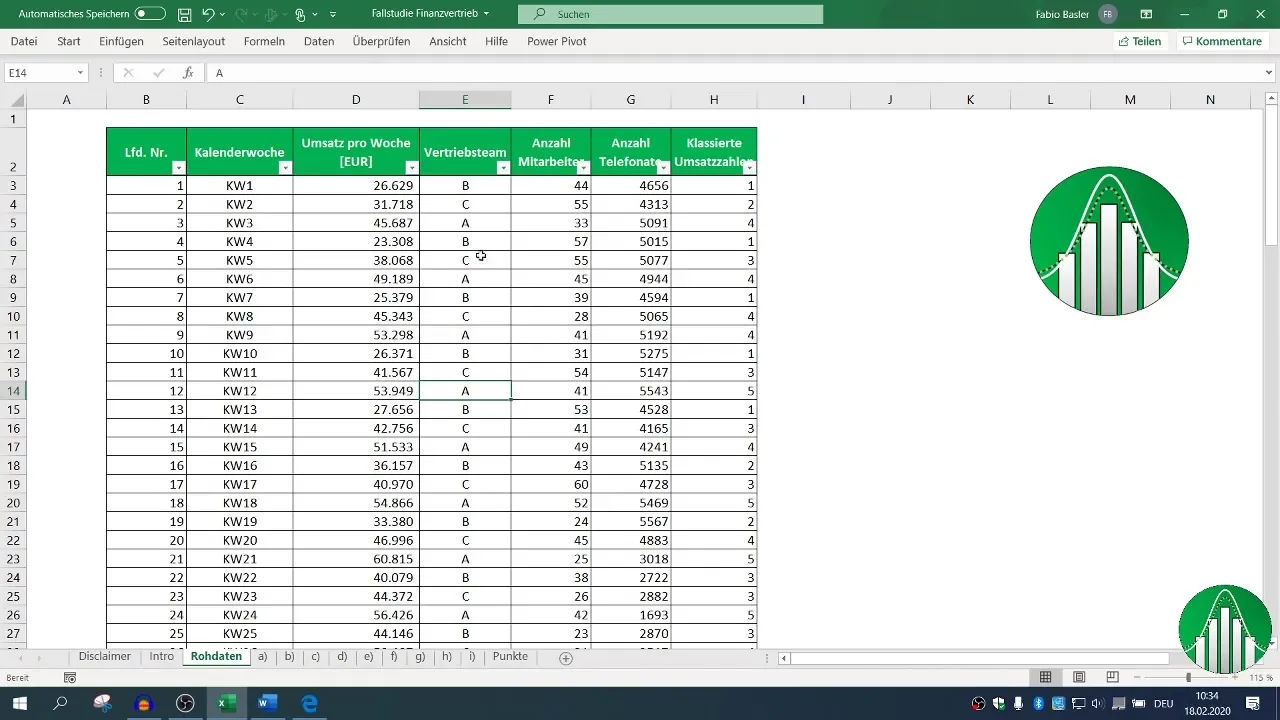
Ennen kuin voit aloittaa analyysin, varmista, että tietosi on oikein muotoiltu Excelissä. Tuo tulos-, työntekijä- ja puhelindata Excel-arkistoon. Varmista, että kaikki tietueet ovat täydellisiä ja tarvittavat muuttujat ovat olemassa.

2. Korrelaatioanalyysin suorittaminen
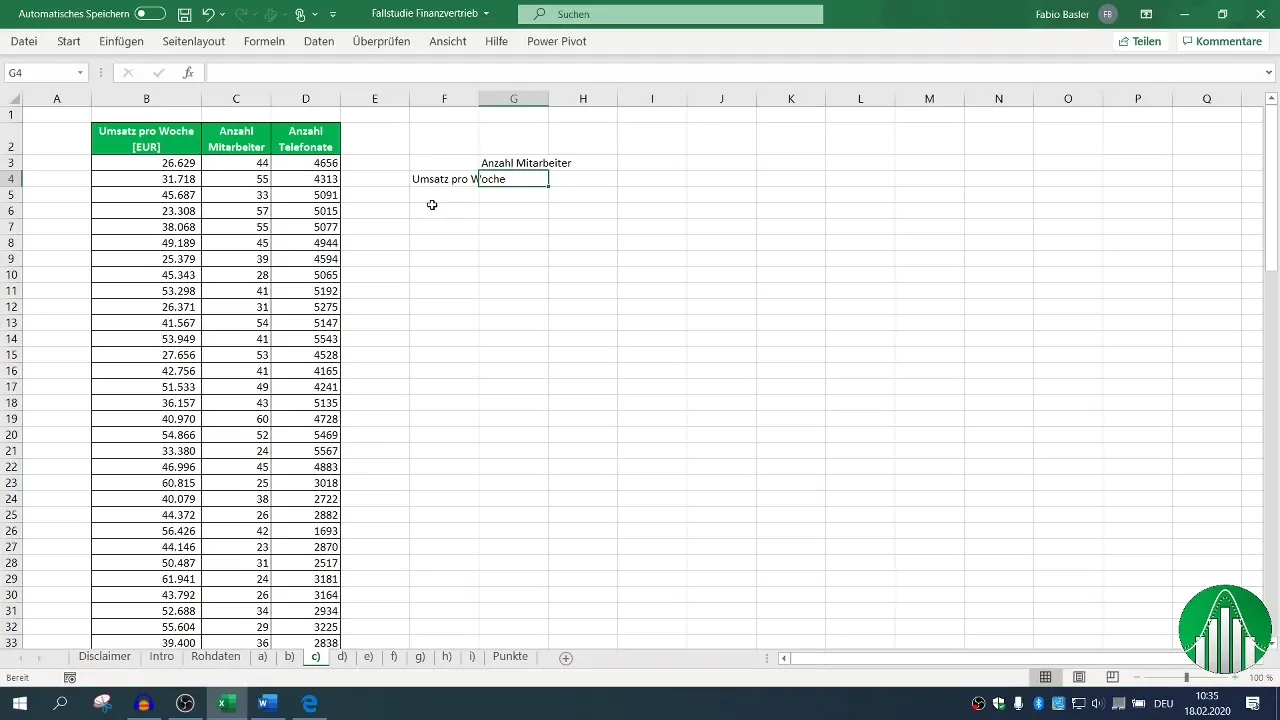
Voit analysoida korrelaatiota liikevaihdon, työntekijöiden ja puheluiden muuttujien välillä laskemalla korrelaatiokertoimen. Tähän voit käyttää Excelin kaavaa =KORREL(). Saadaksesi yleiskuvan kaikista muuttujista, luo korrelaatiomatriisi.
Valitse ensin sopivat sarakkeet liikevaihdolle ja työntekijämäärälle. Kaavalla =KORREL() valitset alueet liikevaihdolle ja työntekijämäärälle. Tulos näyttää yhteyden voimakkuuden.
3. Korrelaatiomatriisin luominen
Lisäanalyyseja varten suositellaan Excelin tietojen analyysitoimintojen käyttämistä. Ota data-analyysi käyttöön, jos et ole tehnyt sitä vielä. Siirry "Data"-välilehteen, valitse "Data-analyysi" ja valitse "Correlation".
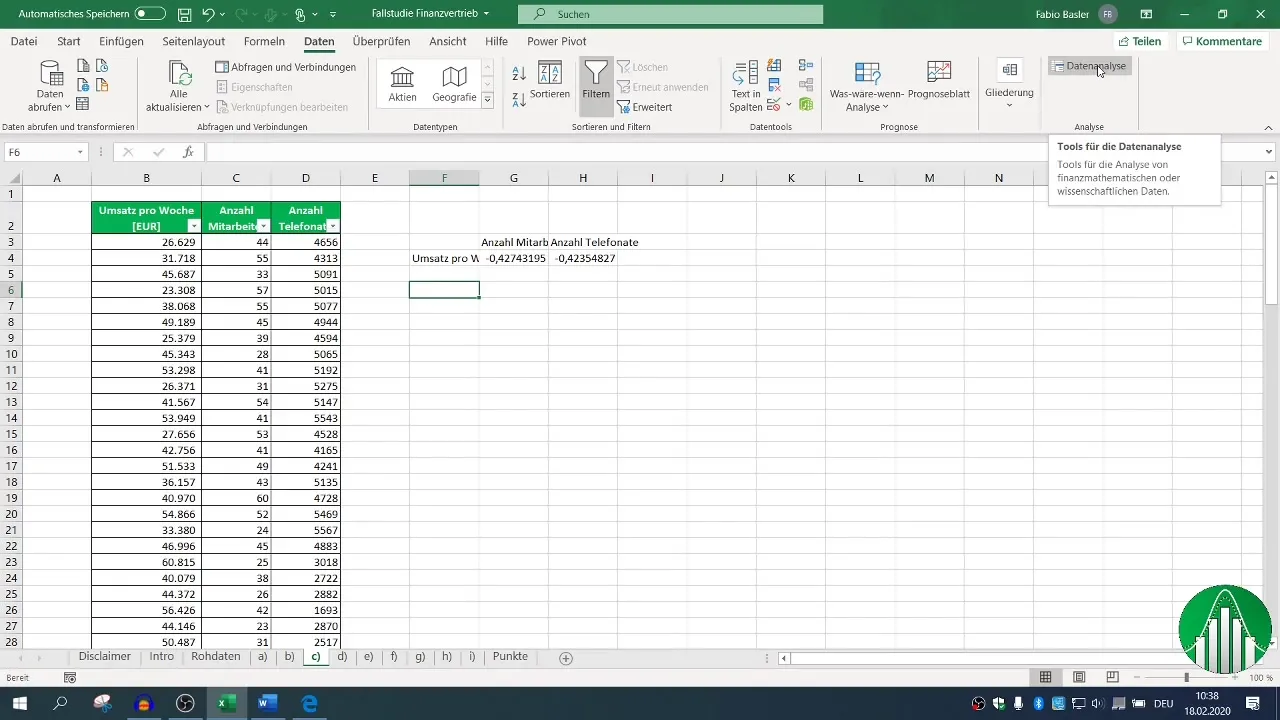
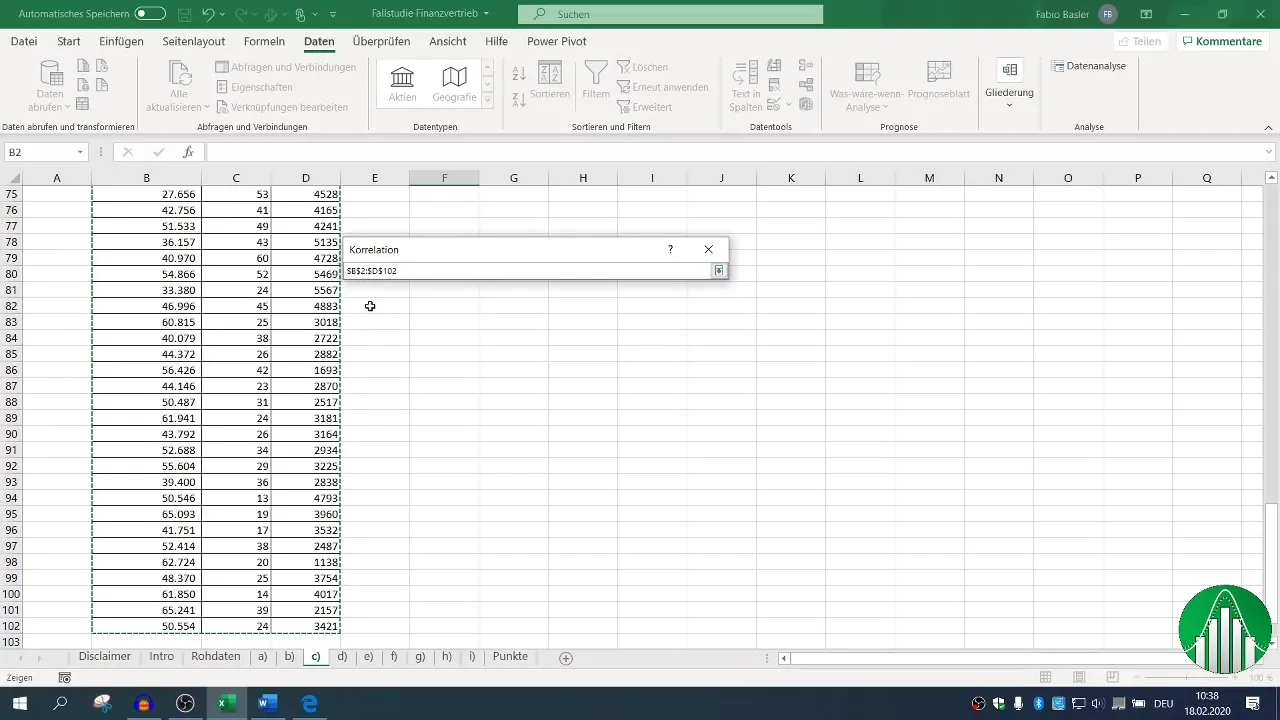
Määritä syöttöalue datallesi ja rastita valintaruutu otsikkotiedoille, jotta Excel tunnistaa otsikot oikein. Kun olet määrittänyt tulostusalueen, voit generoida korrelaatiomatriisin, joka näyttää kaikki oleelliset suhteet.
4. Korrelaatioiden visualisointi
Tulosten havainnollistamiseksi XY-diagrammi voi olla hyödyllinen. Valitse X- ja Y-aineistosi ja pyydä pistepilven generointia.
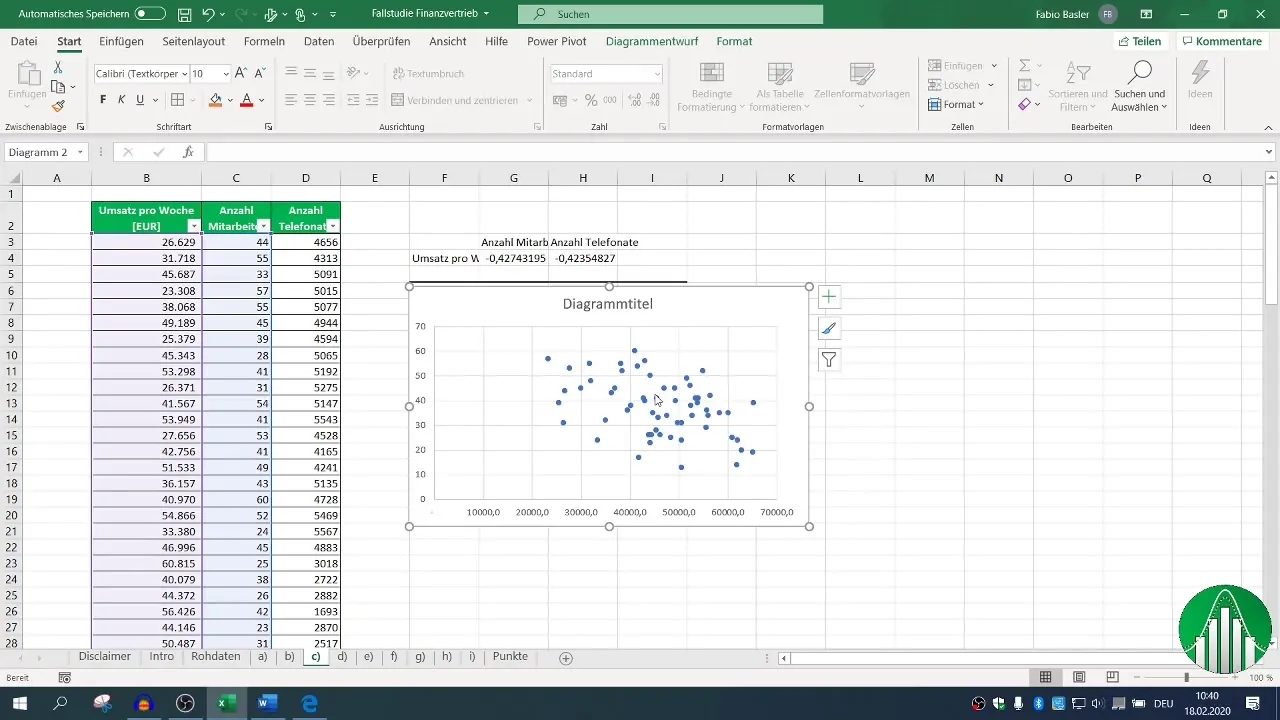
Lisää trendiviiva visuaalisen yhteyden havainnollistamiseksi. Tämä voi tarjota intuitiivisemman käsityksen tiedoista.
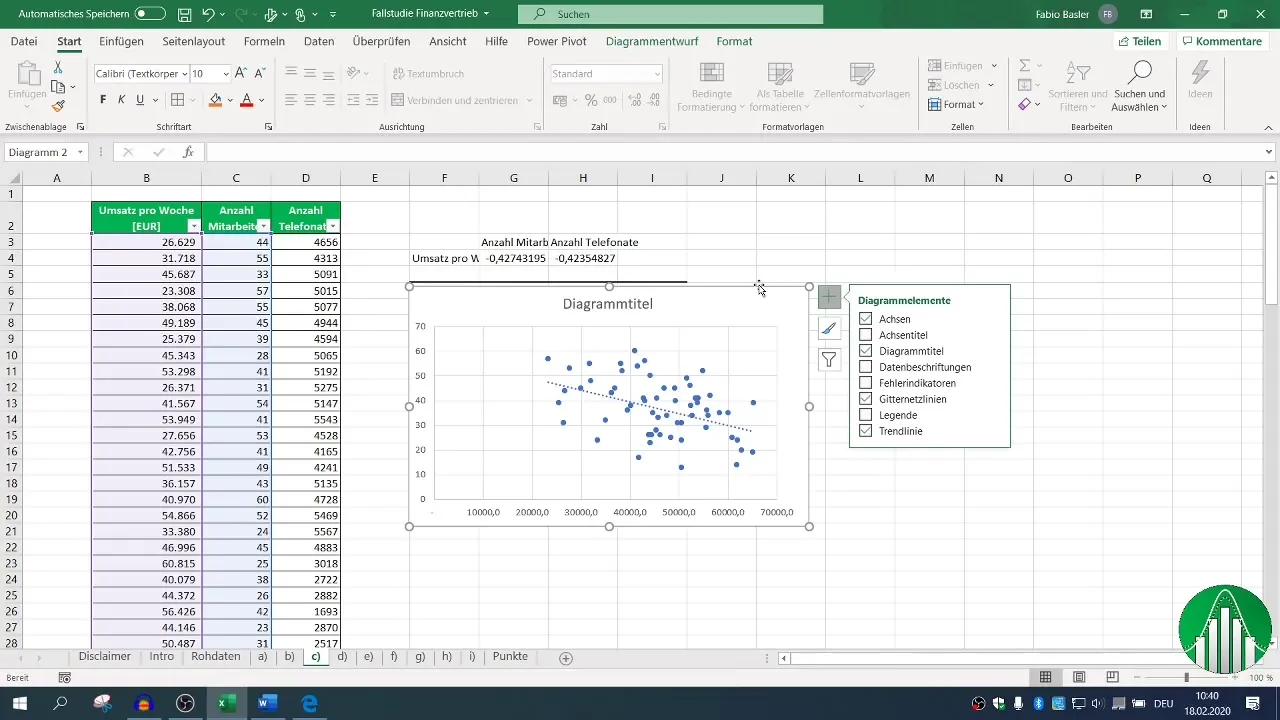
5. Regressioanalyysin suorittaminen
Seuraavaksi on regressioanalyysin vaihe. Siirry uudelleen "Data"-välilehteen ja valitse "Data-analyysi", sitten "Regressio". Määritä syöttöalue riippuvaiselle muuttujalle (liikevaihto) ja riippumattomille muuttujille (työntekijämäärä ja puhelut).
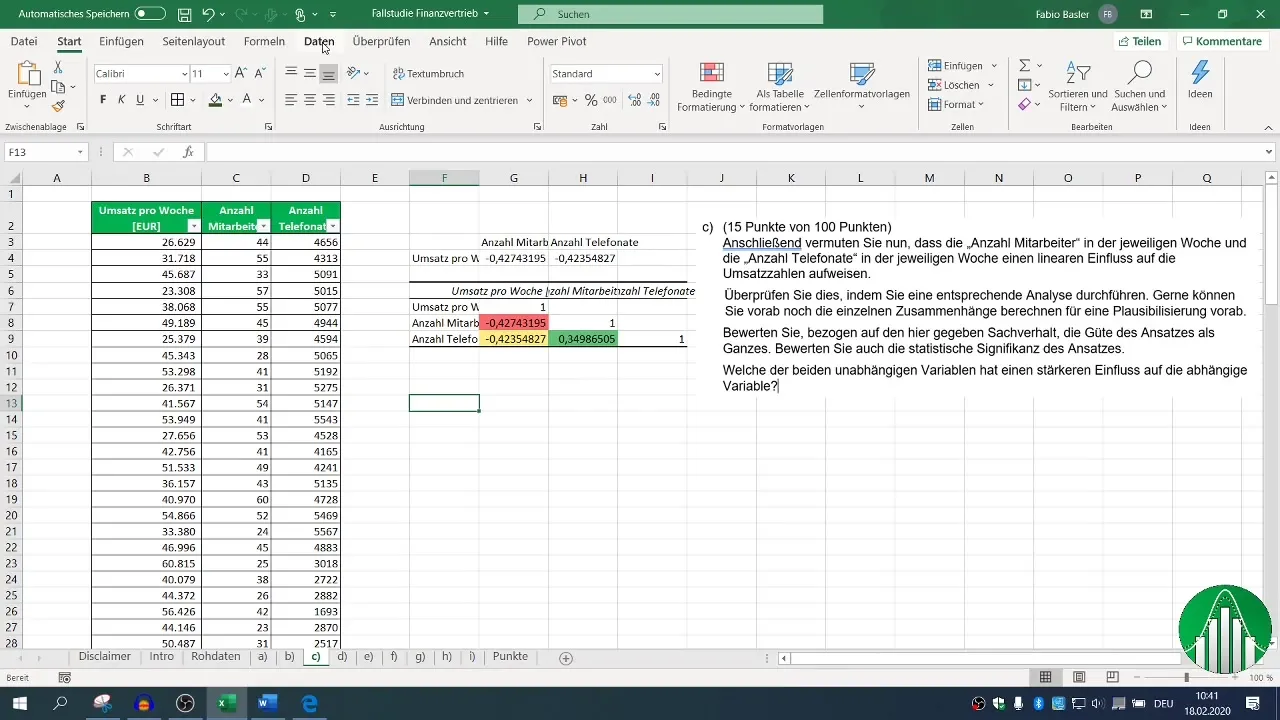
Varmista, että olet määrittänyt otsikon arvoille ja määritä tulostusalueesi. Oletuskonfidenssitaso on asetettu 95 %:iin, mikä riittää useimpiin analysointitapauksiin.
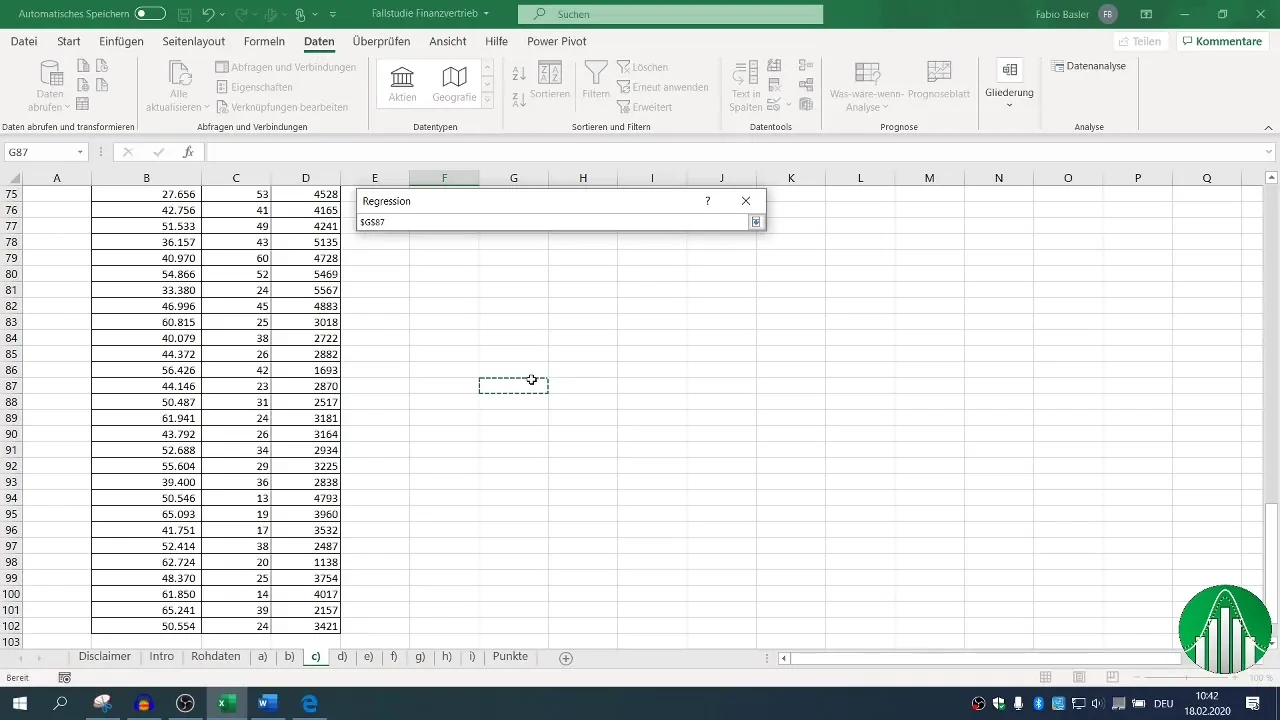
6. Regressioanalyysin arviointi
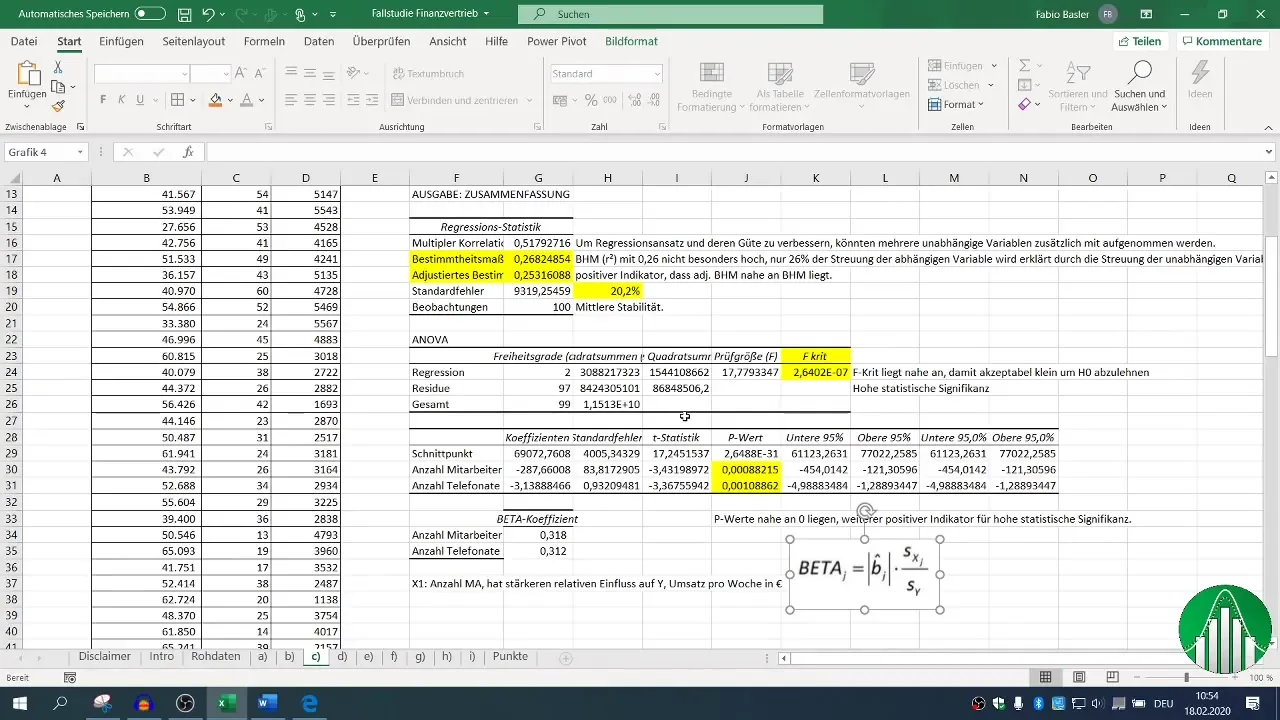
Kun regressioanalyysi on suoritettu, sinulla on erilaisia tulostuslohkoja käytössäsi. Keskitä huomiosi selityskertoimeen (R²), joka kuvaa mallin laatua. R²-arvo 0,26 kertoo, että vain 26 % liikevaihtomuuttujan vaihtelusta selittyy riippumattomien muuttujien avulla.
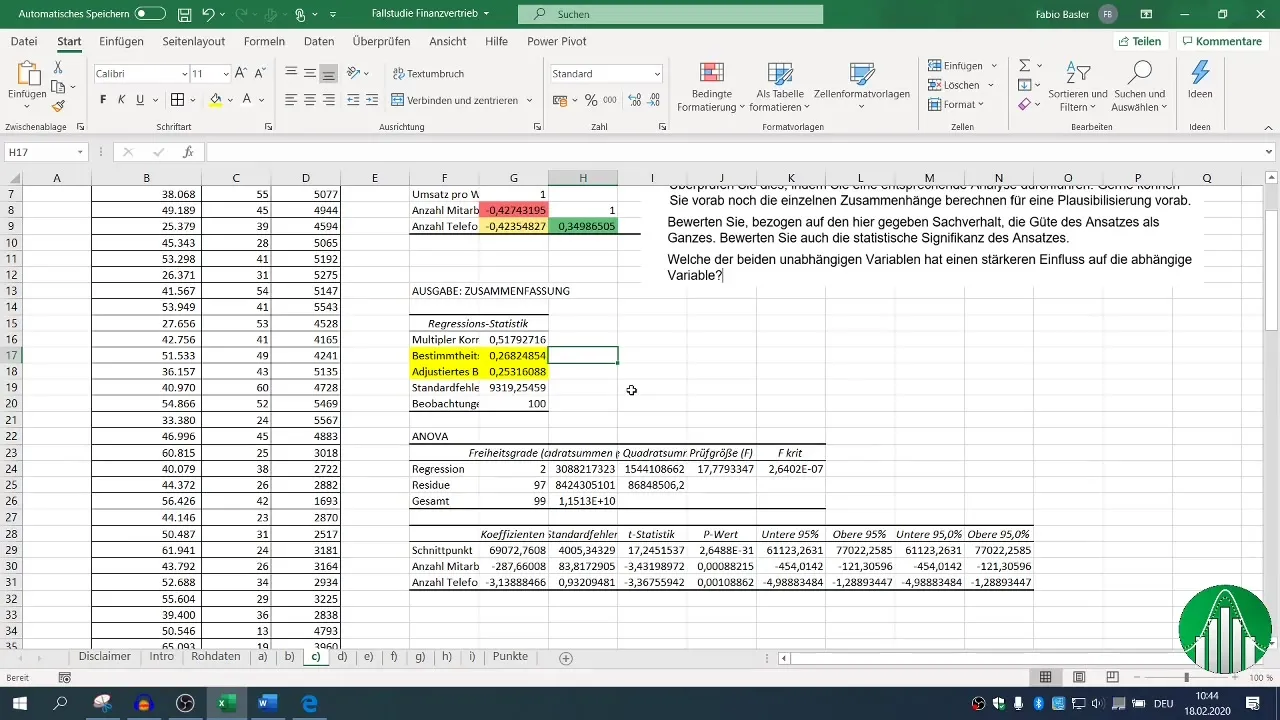
Säädetyssä määräysasteessa tulisi olla lähellä R²-arvoa, mikä tässä tapauksessa on positiivinen indikaattori.
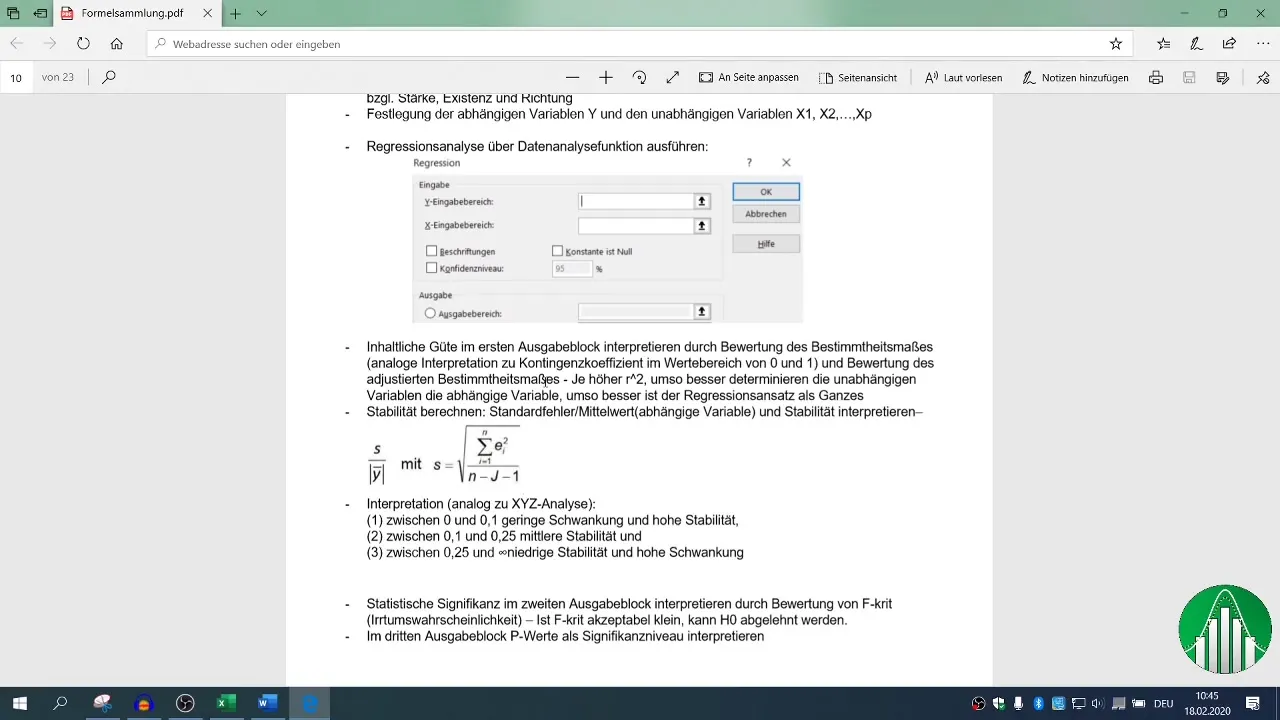
7. Tilastollisen merkitsevyyden arviointi
F-arvo ja riippumattomien muuttujien p-arvot ovat ratkaisevia tilastollisen merkitsevyyden arviointiin. P-arvo alle 0,05 osoittaa, että yhteys on tilastollisesti merkitsevä.
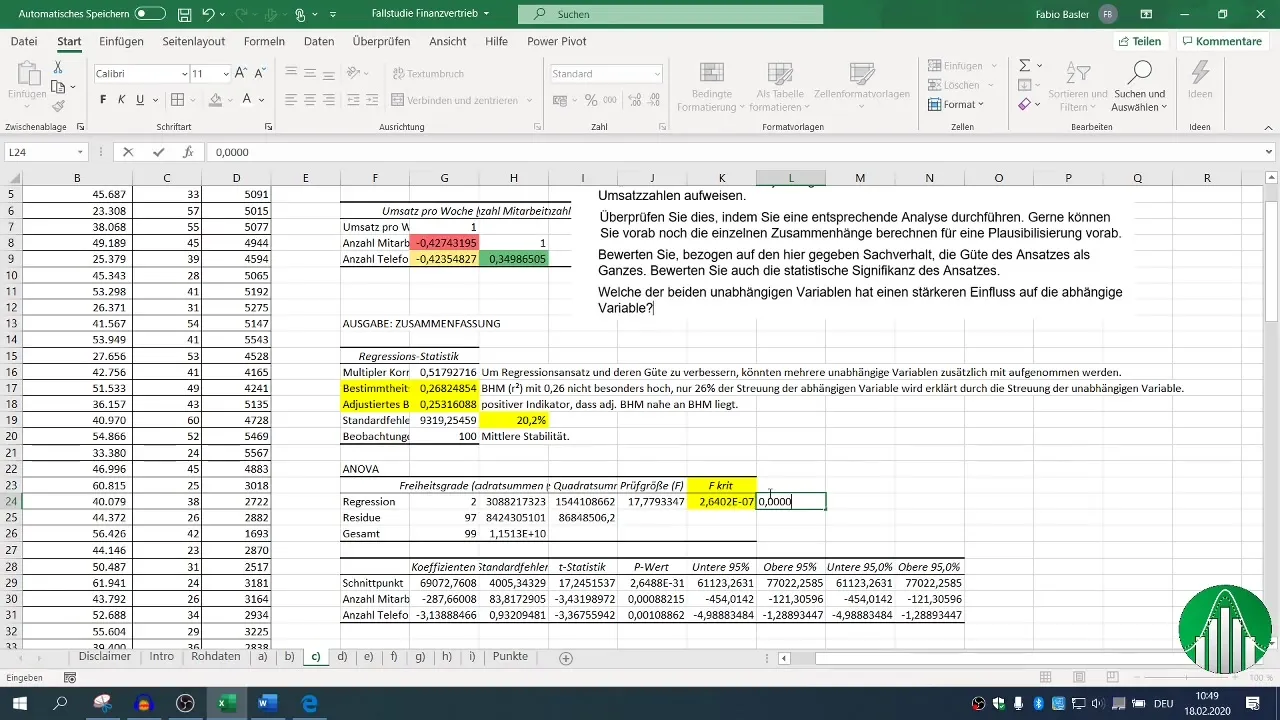
Nämä tilastolliset tunnusluvut yhdistettynä R²-arvoon auttavat sinua ymmärtämään tulostesi vakaudesta ja merkityksellisyydestä.
8. Vaikuttavien tekijöiden vertailu
Lopulta sinua kiinnostaa, mikä tekijä – työntekijöiden määrä vai puhelut – vaikuttaa enemmän liikevaihtoon. Tässä tapauksessa otat beetakertoimet käteesi ja vertaat niitä keskenään.
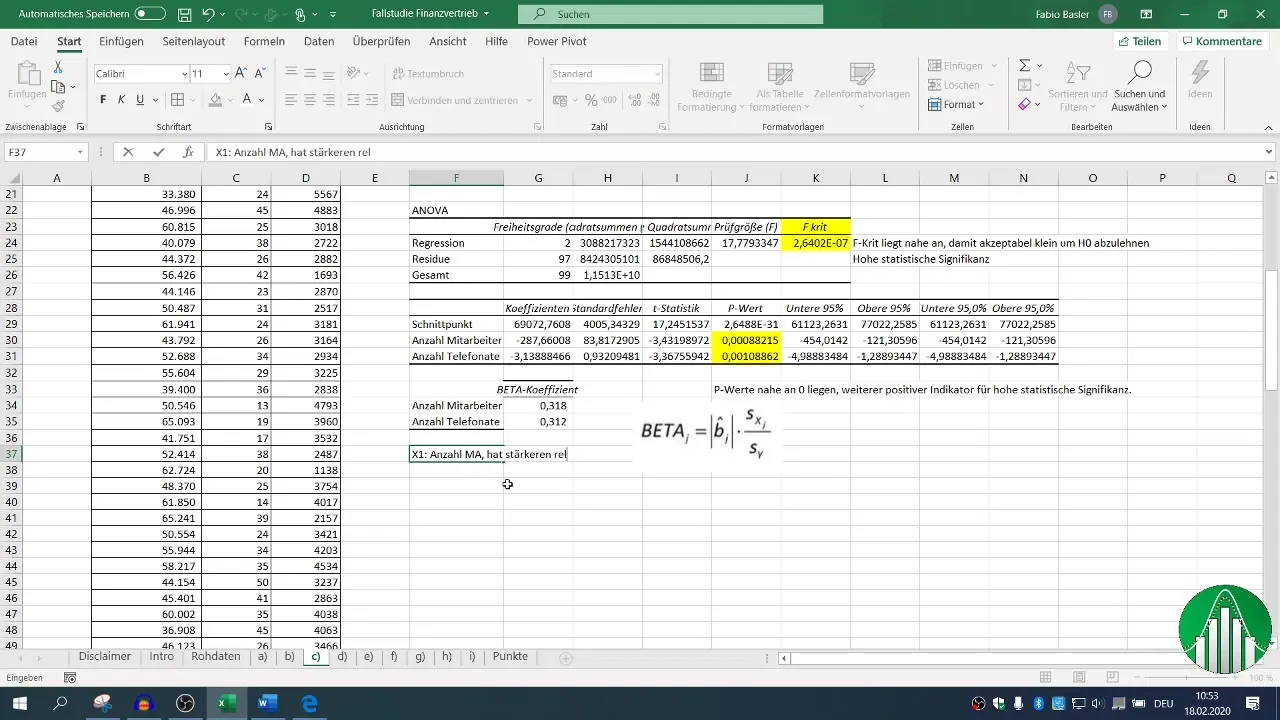
Korkeampi beetakerroin osoittaa suhteellisen vaikutuksen; voi käydä ilmi, että työntekijämäärällä on suurempi vaikutus liikevaihtoon kuin puhelumäärällä.
Yhteenveto
Aiempi analyysi antoi sinulle arvokkaita näkemyksiä tilastollisista suhteista liikevaihdon, työntekijämäärän ja puheluiden välillä. Suorittamalla järjestelmällisesti korrelaatio- ja regressioanalyysit Excelissä voit tehdä päätöksiä, jotka perustuvat tuloksiisi.
Usein kysytyt kysymykset
Miksi korrelaatioanalyysi on tärkeä?Korrelaatioanalyysi auttaa tunnistamaan kahden muuttujan välisen suhteen ennen yksityiskohtaisen regressioanalyysin suorittamista.
Miten tulkitsen R²-arvon regressioanalyysissä?R²-arvo 0,26 tarkoittaa, että 26 % riippuvan muuttujan (liikevaihto) vaihteluista selittyy riippumattomilla muuttujilla.
Mikä on korrelaation ja regressioiden ero?Korrelaatio mittaa kahden muuttujan välistä suhdetta, kun taas regressio arvioi useiden riippumattomien muuttujien vaikutusta yhteen riippuvaan muuttujaan.
Kuinka voin testata tilastollisen merkitsevyyden?Testaat tilastollisen merkitsevyyden p-arvon perusteella; p-arvot alle 0,05 ovat merkitseviä.
Mikä rooli beetakertoimilla on?Beetakertoimet osoittavat riippumattomien muuttujien suhteellisen vaikutuksen riippuvaan muuttujaan.


