Les statistiques sont un outil important pour l'analyse dans de nombreux domaines. Ce guide vous montre comment effectuer l'analyse de corrélation de rang de Spearman dans Excel. Cette méthode vous permet de quantifier efficacement la relation entre des variables ordinales. Nous examinons la relation entre la satisfaction client et le niveau de marketing.
Principales découvertes
- L'analyse de corrélation de rang de Spearman est particulièrement adaptée aux données à échelle ordinale.
- L'utilisation d'Excel permet un calcul rapide et une visualisation de la corrélation de rang.
- Une faible corrélation positive entre les niveaux de marketing et la satisfaction client montre que des investissements supplémentaires dans le marketing ne conduisent pas nécessairement à une satisfaction plus élevée.
Guide étape par étape
Tout d'abord, vous ne pouvez pas éviter d'insérer les données pertinentes. Nous nous concentrons sur la satisfaction client et les niveaux de marketing. Ces données ont été collectées dans le cadre d'une étude de cas.
Vous pouvez commencer par copier les données de votre ensemble de données brut et les coller dans une nouvelle feuille de travail. Assurez-vous de définir clairement les en-têtes de colonnes. Il pourrait être utile de nommer les colonnes "Satisfaction client" et "Niveau de marketing".
Une fois que vous avez copié les données, il est important de vérifier les niveaux d'échelle de vos variables. La satisfaction client est à échelle ordinale, tout comme les niveaux de marketing qui sont également catégorisés de manière ordinale. Vous devez vous assurer d'avoir correctement compris cela pour éviter toute erreur lors du calcul ultérieur.
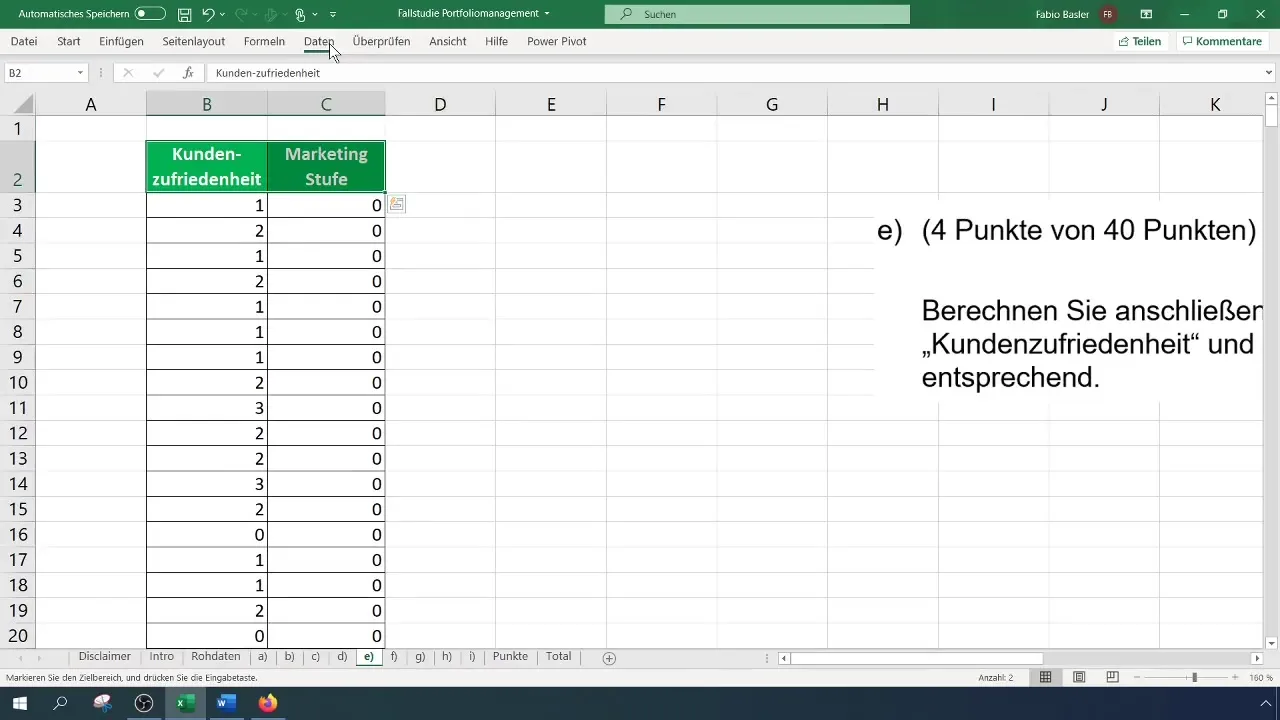
La prochaine étape consiste à préparer les données pour l'analyse de corrélation de rang. Vous avez besoin des rangs des variables. Dans Excel, cela se fait avec la fonction "RANG.EQUIV" ou "RANG.MOYEN". Cette fonction attribue un rang à chaque nombre par rapport à une matrice définie. Assurez-vous de travailler dans la plage correcte.
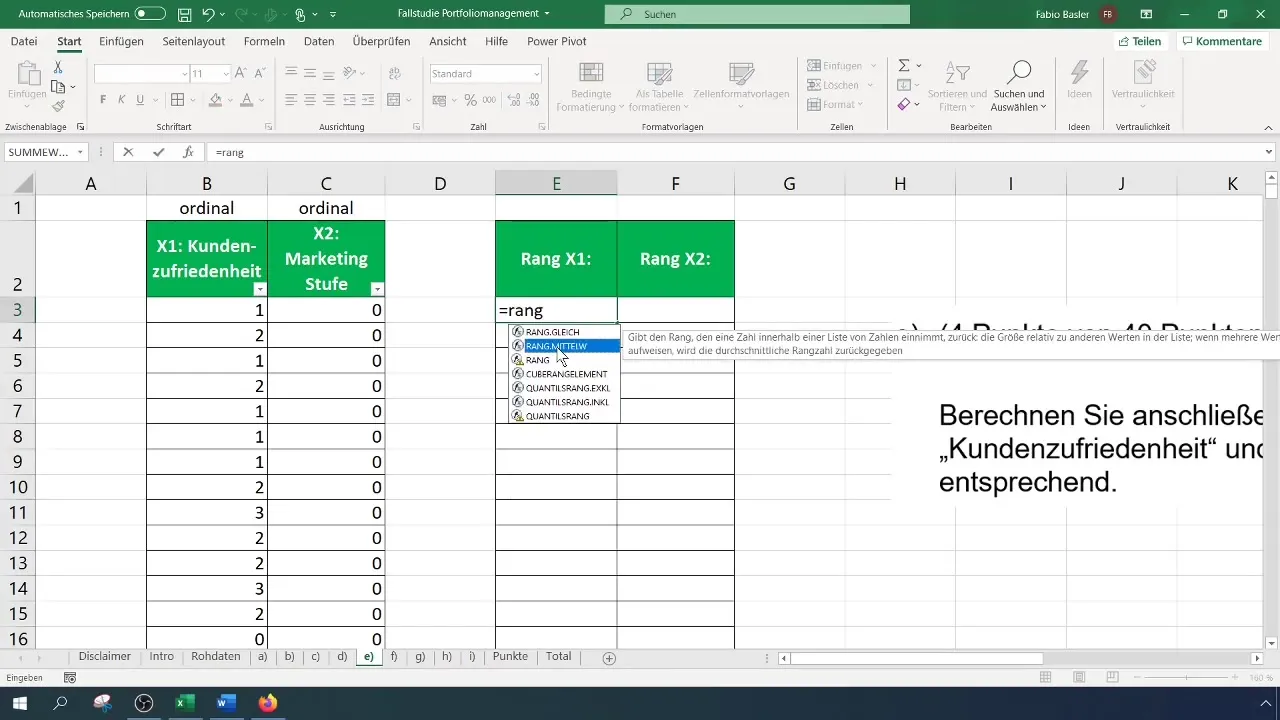
Pour calculer les rangs de la satisfaction client, que nous désignons ici par la variable X1, vous sélectionnez d'abord la cellule correspondante. Pour la première observation, cela signifie sélectionner la cellule de la satisfaction client, puis choisir la matrice dans laquelle les rangs seront déterminés. Il est important de fixer le référencement pour l'ensemble de la matrice afin que le référencement ne change pas lorsque vous faites glisser la formule vers le bas.
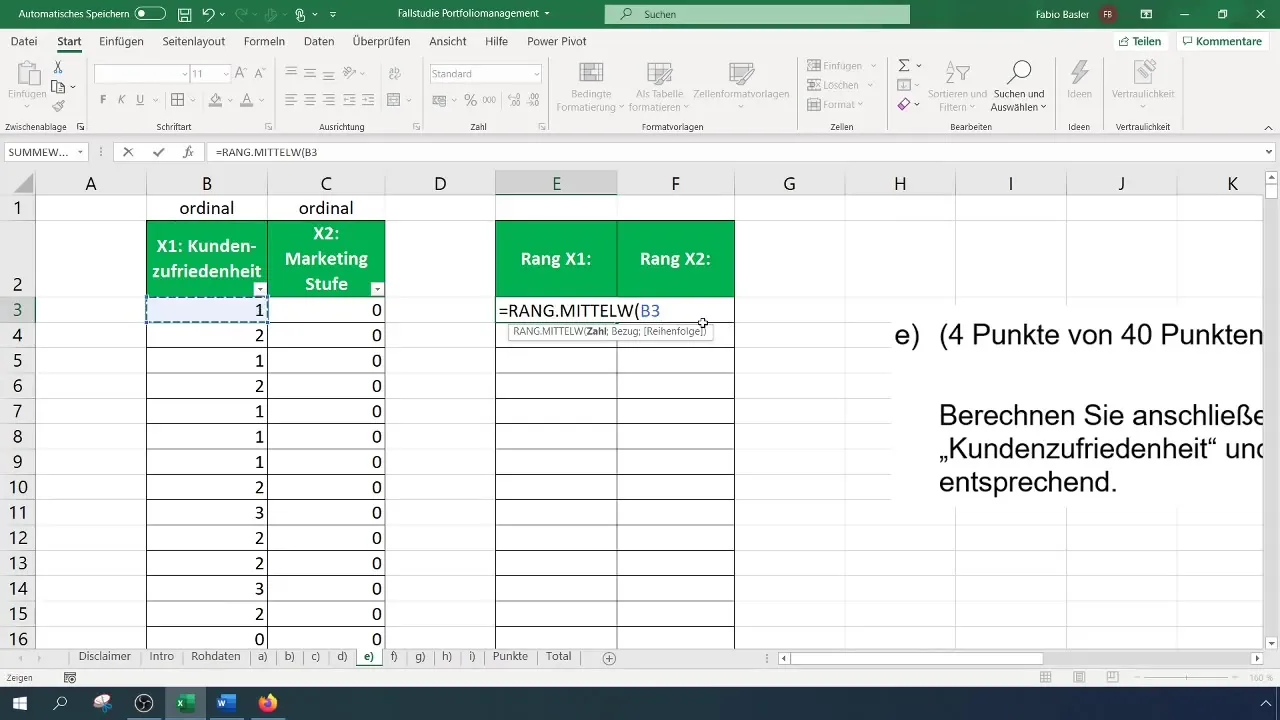
Pour calculer les rangs du niveau de marketing (X2), vous répétez le même processus. Ici aussi, il est important de conserver l'intégralité de la plage de données pour que la formule fonctionne correctement lorsque vous la copiez vers le bas. Ces étapes garantissent que les rangs de chaque variable sont correctement déterminés.
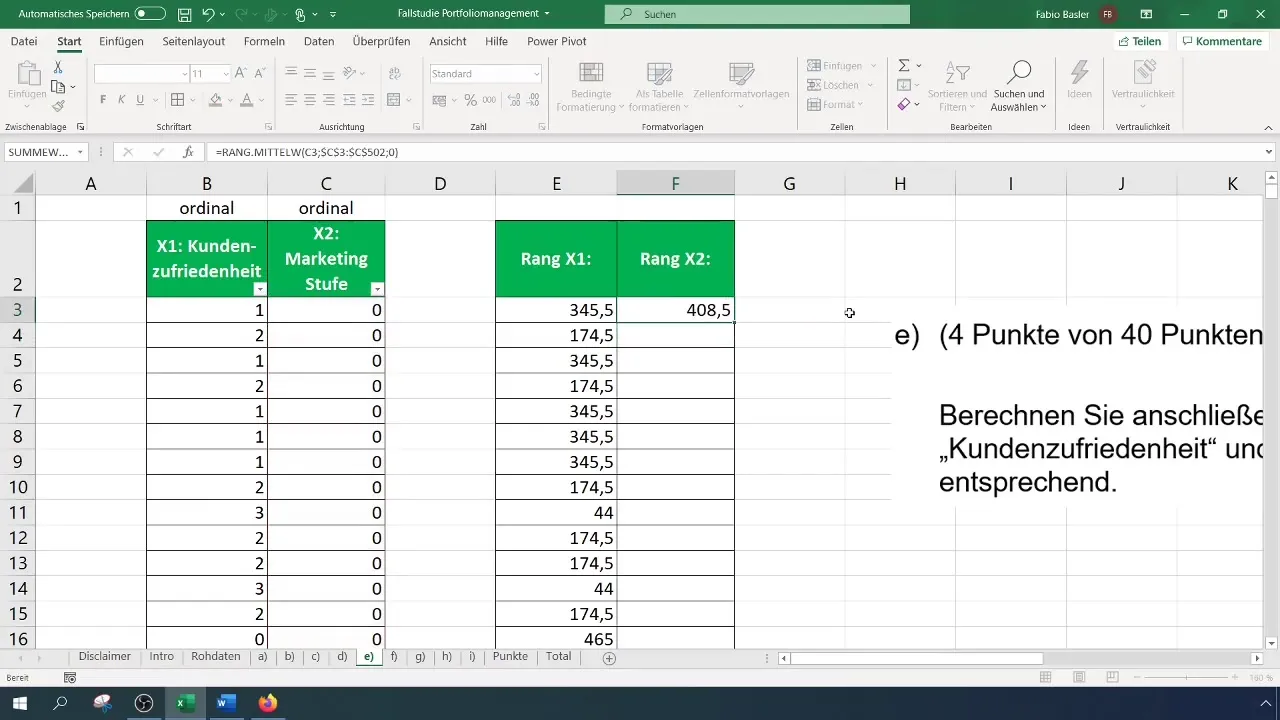
Une fois que vous avez les rangs pour les deux variables, vous pouvez calculer la corrélation de rang. Cela se fait avec la fonction "CORREL". Cette fonction vous permet de sélectionner les rangs à la fois de X1 et de X2 et de calculer la corrélation. Le résultat vous indiquera la force de la relation entre les deux variables.
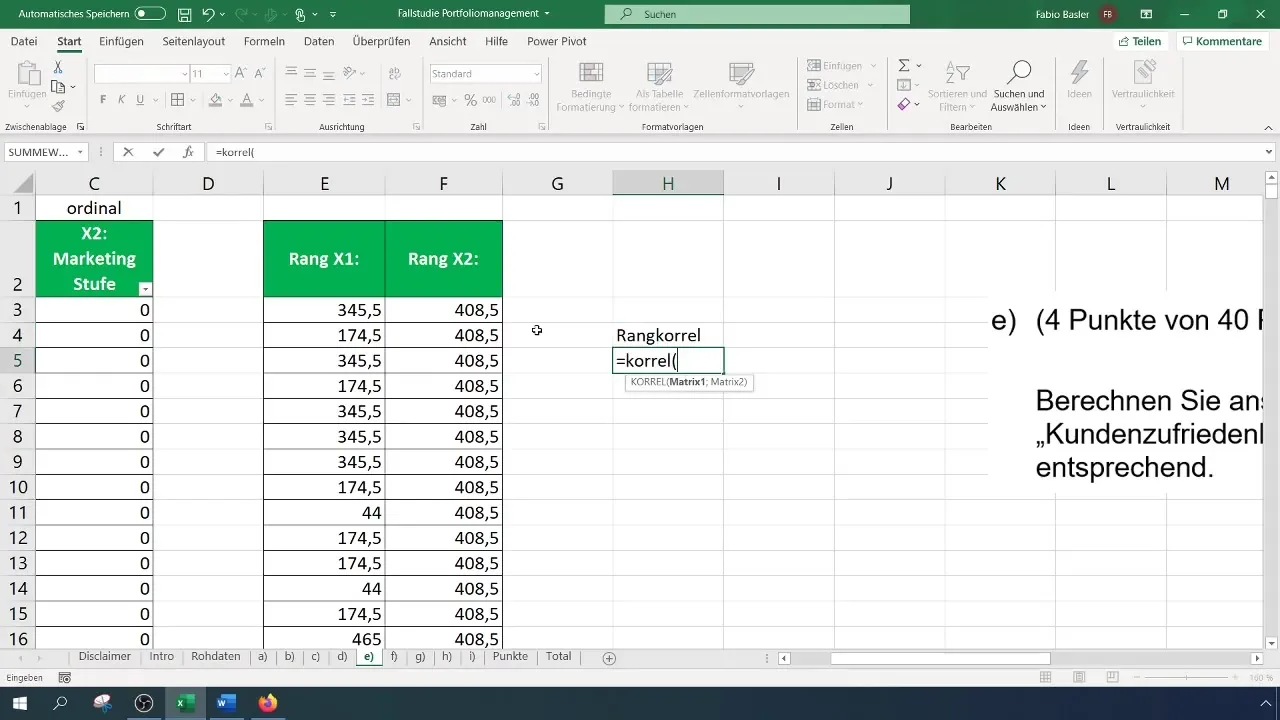
Dans votre cas, la corrélation est de 0,082, ce qui indique une faible corrélation positive. Ce chiffre montre qu'il y a une tendance selon laquelle des dépenses marketing plus élevées entraînent une meilleure satisfaction client, mais cette relation n'est pas forte.
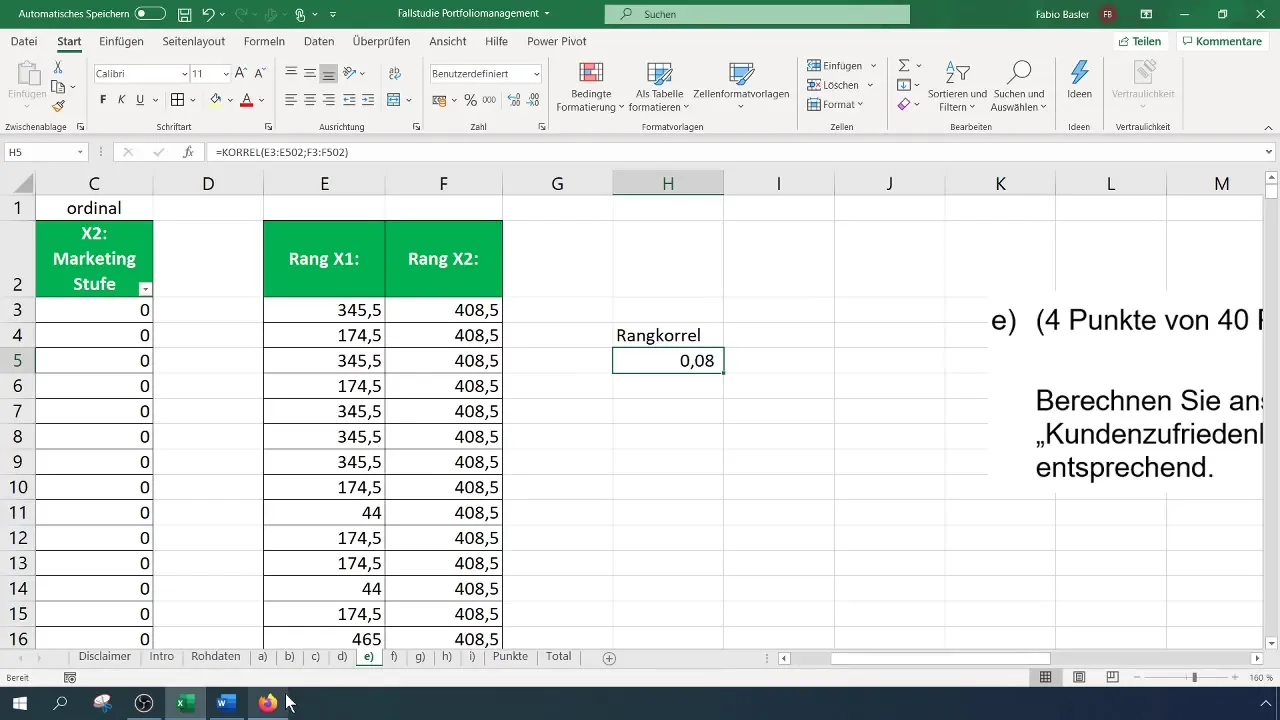
Enfin, vous devriez documenter l'interprétation de vos résultats. Un tableau pourrait vous aider à montrer où se situe la corrélation de rang et à clarifier la relation entre les deux variables.
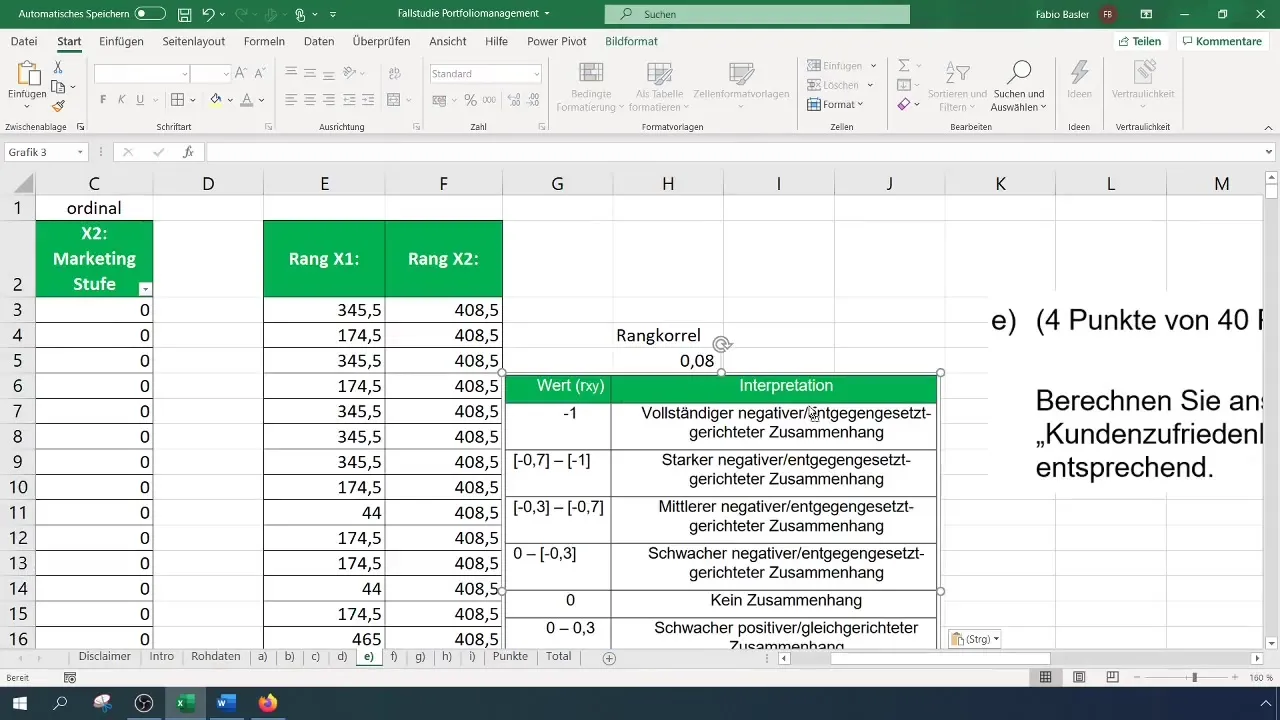
L'approche de l'analyse de corrélation des rangs aide à obtenir des insights qualitatifs à partir de données quantitatives et montre comment les dépenses marketing pourraient varier sans nécessairement augmenter la satisfaction des clients.
Résumé
Dans ce tutoriel, vous avez appris comment réaliser l'analyse de corrélation des rangs dans Excel. Vous avez d'abord préparé correctement vos données, puis déterminé les rangs des deux variables. Enfin, vous avez calculé la corrélation des rangs pour quantifier la relation entre le niveau de marketing et la satisfaction des clients.


