Les tests statistiques sont un élément central de l'analyse des données et de la prise de décision. En particulier dans le domaine de la biotechnologie, il peut être crucial de vérifier des hypothèses concernant le taux de succès des agents actifs. Dans le cadre de ce tutoriel, vous apprendrez comment effectuer un test unilatéral (test 1SP) pour l'espérance avec une variance connue de manière efficace dans Excel.
Principales conclusions
Ce guide vous transmettra :
- Les bases théoriques du test unilatéral.
- Les étapes pour effectuer le test dans Excel.
- L'interprétation des résultats.
Préparation des données
Pour effectuer le test unilatéral dans Excel, vous avez besoin des données pertinentes. Dans notre exemple, nous supposons que vous analysez le taux de succès des agents actifs. Il est connu que le taux de succès moyen était auparavant de 59 %, avec un écart-type de 19. Vous devriez d'abord insérer vos données dans un tableau Excel.
Assurez-vous d'organiser vos données en colonnes pour pouvoir y accéder plus tard. Une belle clarté vous aidera à suivre plus facilement les étapes individuelles.
Aperçu du test
Le test unilatéral vise à vérifier si la valeur moyenne du succès diffère significativement d'une valeur donnée. Dans ce cas, nous vérifions si le taux de succès de 59 % peut être nettement augmenté à l'avenir.
Formulation des hypothèses
Les hypothèses que vous formulez pour le test sont cruciales :
- Hypothèse nulle (H0) : La vraie valeur moyenne est égale à 59 (σ = 59 %).
- Hypothèse alternative (H1) : La vraie valeur moyenne est plus grande que 59 %.
Lors de la formulation des hypothèses, le focus doit être mis sur ce qui doit être testé et comment cela se présente dans votre contexte.
Il est important de bien comprendre la différence entre l'hypothèse nulle et l'hypothèse alternative, car elles constituent la base des calculs suivants.
Collecte de l'échantillon
Pour notre test, nous prenons un échantillon de 500 agents actifs. Il est important de noter que la sélection de l'échantillon doit être représentative et garantir, par la méthode appropriée, que vos résultats peuvent être transférés à la population totale de manière réaliste.
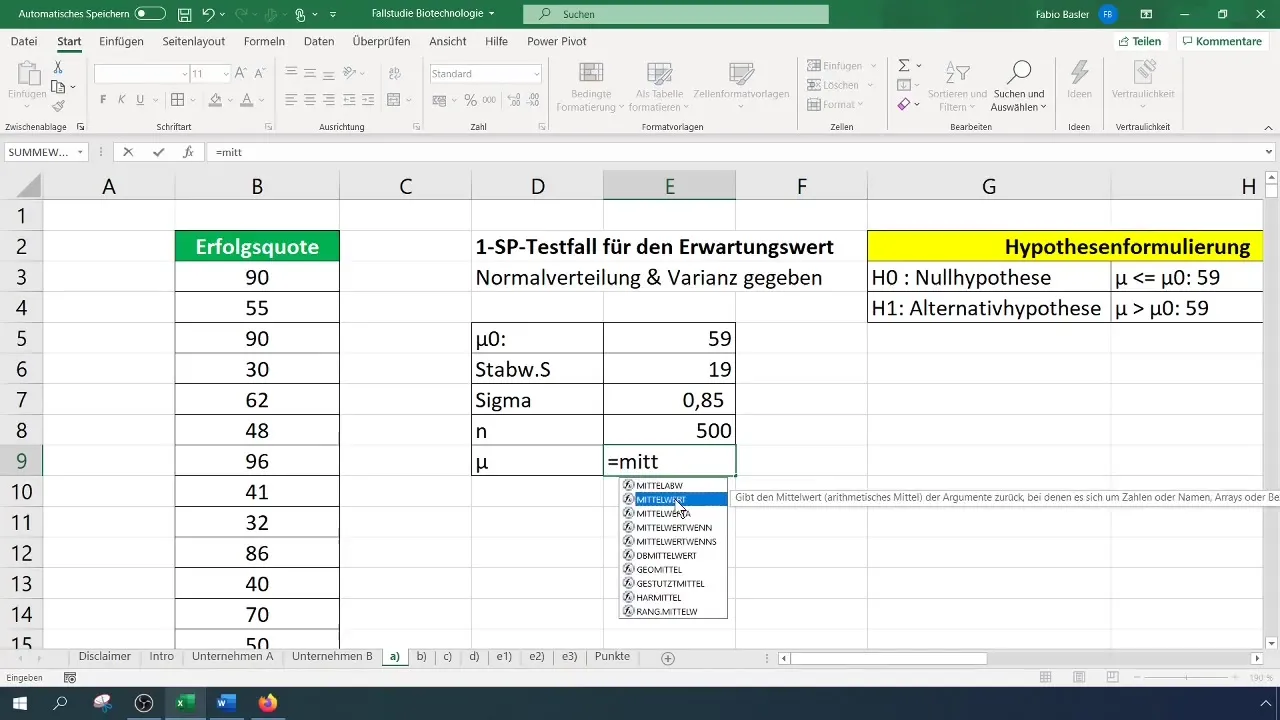
Pour le test, commencez par calculer la moyenne arithmétique. Cela devrait être facile à réaliser en utilisant la formule appropriée dans Excel.
Calcul de la statistique de test
La statistique de test pour un test unilatéral est déterminée par la formule suivante :
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Ici, (\bar{x}) représente la moyenne de votre échantillon, (\mu_0) est la moyenne supposée (dans ce cas 59), (\sigma) est l'écart-type (ici 19), et (n) est le nombre d'échantillons (500).
Une fois que vous avez inséré les valeurs dans la formule, calculez la statistique de test pour déterminer si elle est significative ou non.
Détermination de la valeur critique
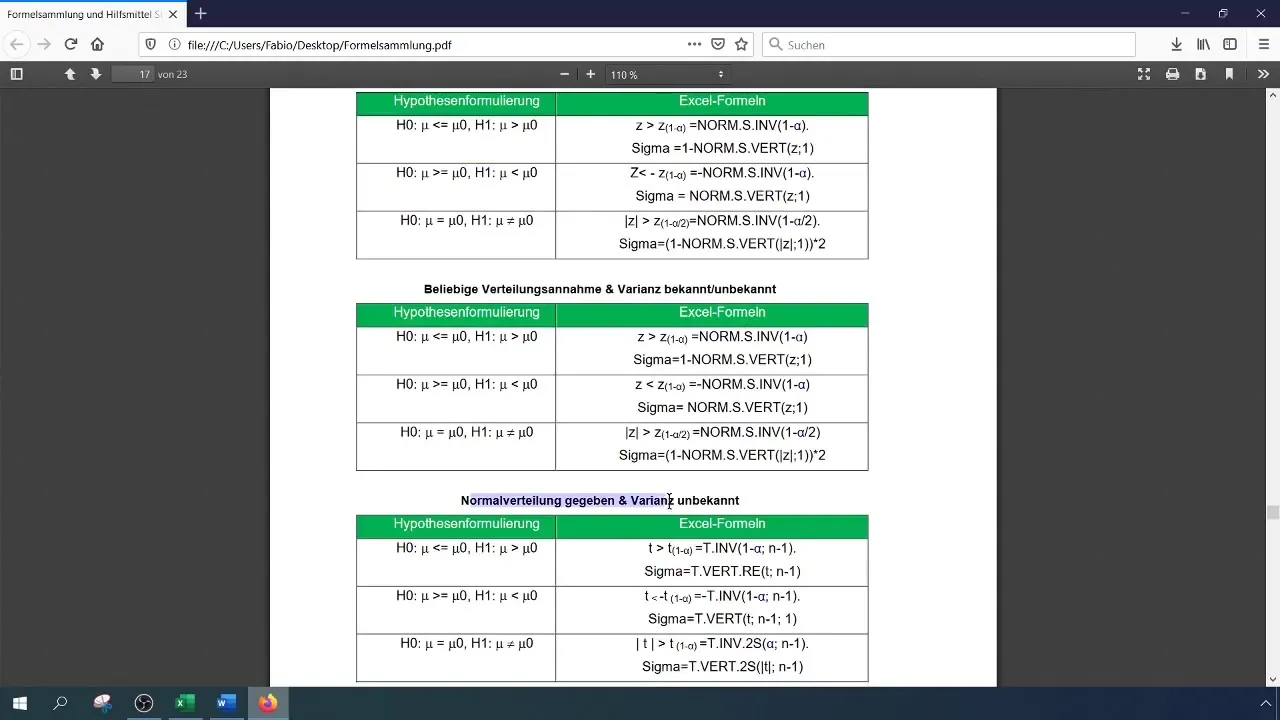
Pour un niveau de signification de 1 % (0,01), vous devez lire ou calculer la valeur critique. Vous pouvez le faire dans Excel avec la fonction NORM.S.INV.
La formule est la suivante :
[ \text{NORM.S.INV}(1 - \alpha) ]
Ici, (\alpha) est le niveau de signification (0,01). La valeur déterminée servira de base pour la comparaison avec la statistique de test.
Exécution du test
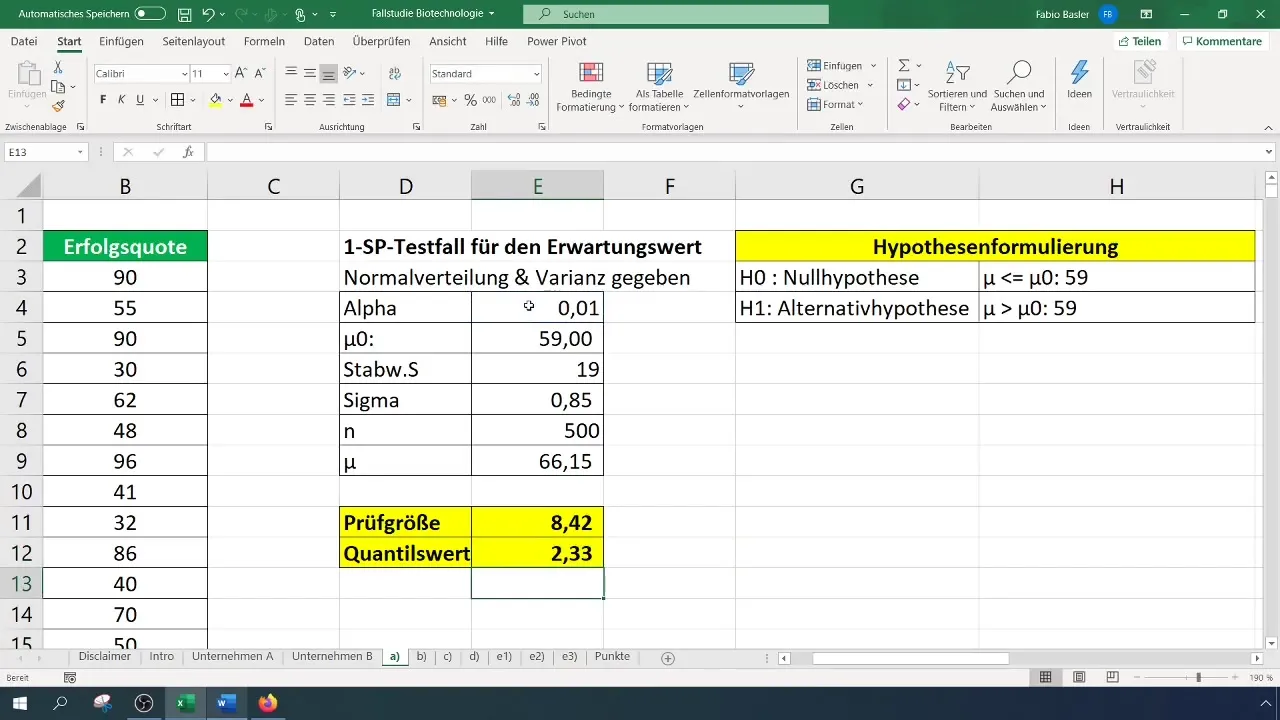
Après avoir obtenu à la fois la statistique de test et la valeur critique, comparez les deux :
- Si la statistique de test est supérieure à la valeur critique, la nullité est rejetée.
- Autrement, vous ne pouvez pas rejeter la nullité.
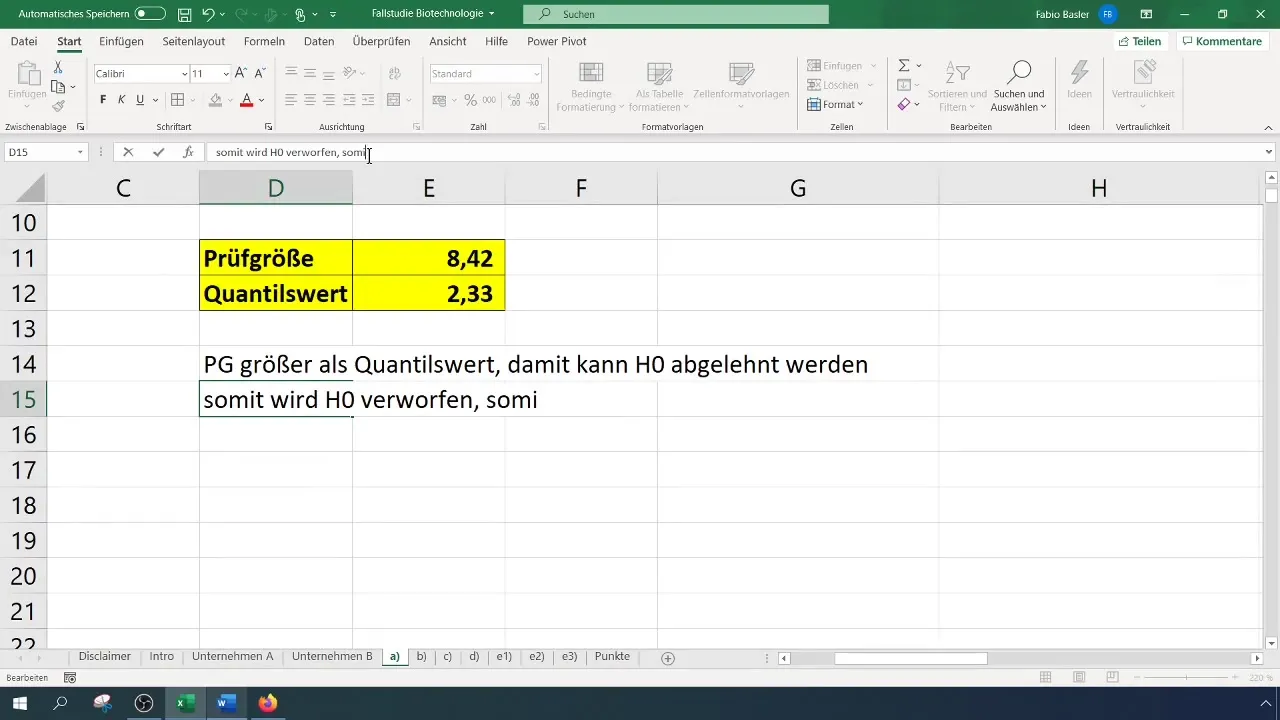
Dans notre cas, nous obtenons une statistique de test de 8,4, qui dépasse la valeur critique de 2,33. Par conséquent, nous pouvons rejeter l'hypothèse nulle. Cela suggère que le taux de réussite a été significativement amélioré.
Interprétation des résultats
Après avoir effectué le test et obtenu les résultats, vous devriez les interpréter dans un contexte clair. Le rejet de l'hypothèse nulle signifie que la nouvelle valeur testée diffère significativement du passé, dans ce cas, les 59 %.
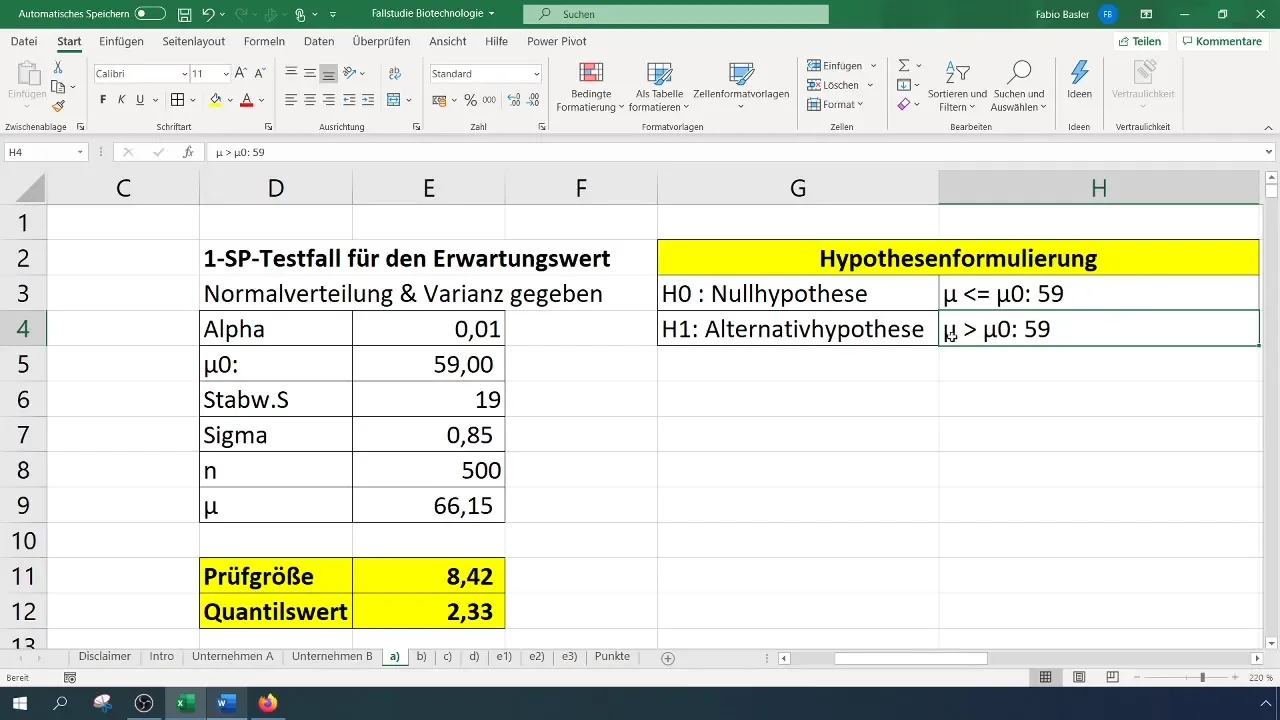
Ces informations sont d'une importance capitale pour la prise de décisions stratégiques au sein de votre entreprise. Elles confirment que les efforts pour améliorer le taux de réussite ont été efficaces.
Conclusion
Dans ce tutoriel, vous avez appris à effectuer un test 1-SP pour la valeur attendue dans Excel. À travers une étude de cas, vous avez pu suivre les étapes de la formulation des hypothèses au calcul des données en passant par l'interprétation des résultats. Ces connaissances sont précieuses non seulement pour les évaluations scientifiques, mais aussi pour les applications pratiques en entreprise.
Questions fréquemment posées
Qu'est-ce que le test 1-SP ?Le test 1-SP est un test statistique permettant de vérifier si la moyenne d'un échantillon diffère significativement d'une valeur prédéfinie.
Comment formuler des hypothèses pour le test ?Les hypothèses se composent d'une hypothèse nulle (H0) et d'une hypothèse alternative (H1) documentant l'état à tester.
Comment calculer la statistique de test ?La statistique de test est déterminée par la formule ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ).
Que se passe-t-il si la statistique de test est supérieure à la valeur critique ?Si la statistique de test est supérieure à la valeur critique, l'hypothèse nulle est rejetée.
Quel est le rôle du niveau de signification ?Le niveau de signification indique avec quelle probabilité vous êtes prêt à accepter une erreur en rejetant à tort l'hypothèse nulle.


