Les tests statistiques sont un élément indispensable de l'analyse des données, en particulier lorsqu'il s'agit de vérifier les différences entre groupes. Une méthode éprouvée, fréquemment utilisée dans la recherche et l'économie, est le test F à deux échantillons. Ce guide vous montre pas à pas comment réaliser un tel test avec Excel pour comparer les variables de dépenses de recherche de deux sociétés pharmaceutiques.
Principales conclusions
- Vous apprendrez comment comparer la variance de deux groupes à l'aide d'un test F.
- Le guide comprend des étapes détaillées pour effectuer le test dans Excel, y compris l'utilisation de la fonction d'analyse des données.
- À la fin, vous saurez comment interpréter les résultats et quelles conclusions en tirer.
Guide étape par étape
Étape 1 : Préparation des données
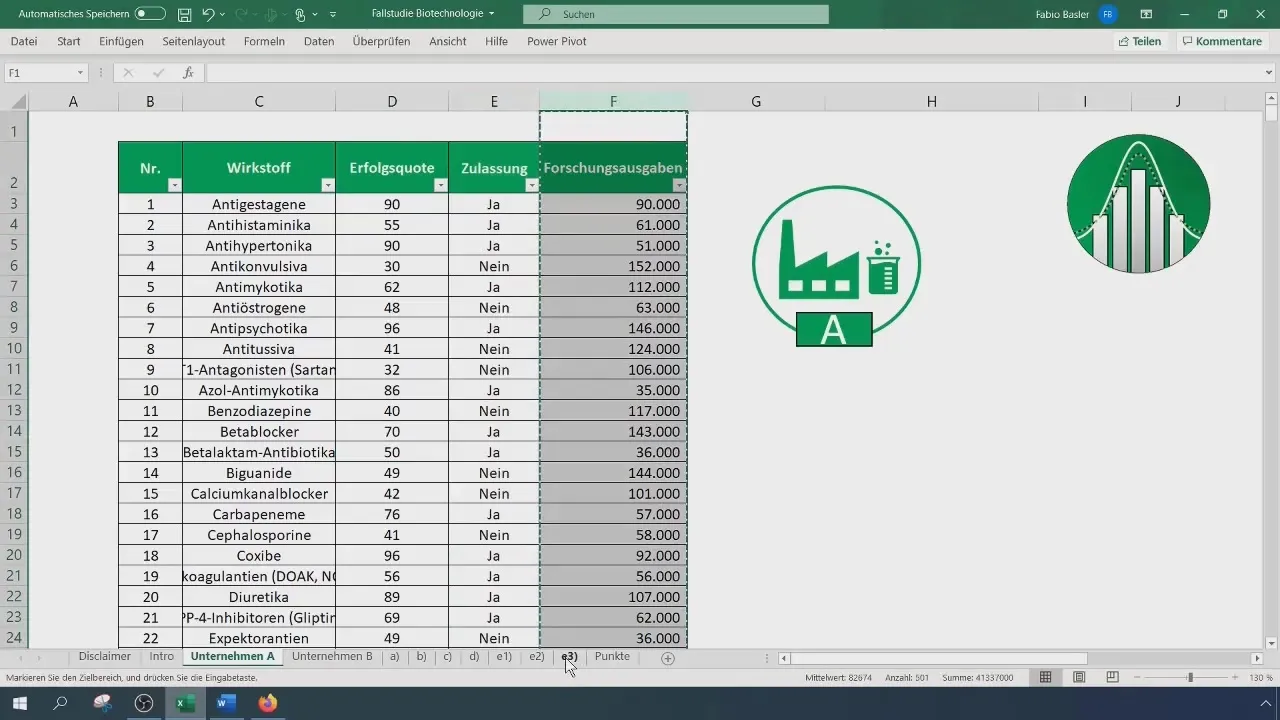
Vous avez besoin des données brutes des dépenses de recherche des deux entreprises. Ouvrez votre fichier Excel et copiez les données de recherche respectives des deux entreprises dans des colonnes séparées.

Étape 2 : Calcul du nombre d'échantillons et de la variance
Votre taille d'échantillon reste la même avec 500 pour l'entreprise A et 100 pour l'entreprise B. Pour calculer la variance des données, utilisez la fonction VAR.S() pour estimer la variance des groupes. Veillez à entrer les valeurs au format Excel pour obtenir des résultats précis.
Étape 3 : Formuler les hypothèses
Pour le test F, les hypothèses doivent être formulées comme suit :
- Hypothèse nulle (H0) : σ1² = σ2² (Les variances des deux entreprises sont égales).
- Hypothèse alternative (H1) : σ1² ≠ σ2² (Les variances des deux entreprises sont différentes).
Étape 4 : Calcul de la statistique de test
Calculez la statistique de test (F-statistique) en divisant les deux variances. Utilisez la formule Variance_A / Variance_B. Si vous avez entré les variances correctement, vous obtiendrez une statistique F pour la comparaison.
Étape 5 : Détermination de la valeur critique
Pour déterminer la valeur F critique, vous avez besoin du niveau d'alpha (généralement 0,05) et des degrés de liberté. Les degrés de liberté se calculent comme suit : dl1 = n1 - 1 et dl2 = n2 - 1. Calculez la valeur critique avec la fonction F.INV().

Étape 6 : Prise de décision
Comparez la statistique F calculée avec la valeur F critique. Si la statistique F est supérieure à la valeur critique, rejetez l'hypothèse nulle ; sinon, ne la rejetez pas. Dans cet exemple, le critère de rejet est que la statistique de test doit être inférieure à la valeur quantile (F critique).

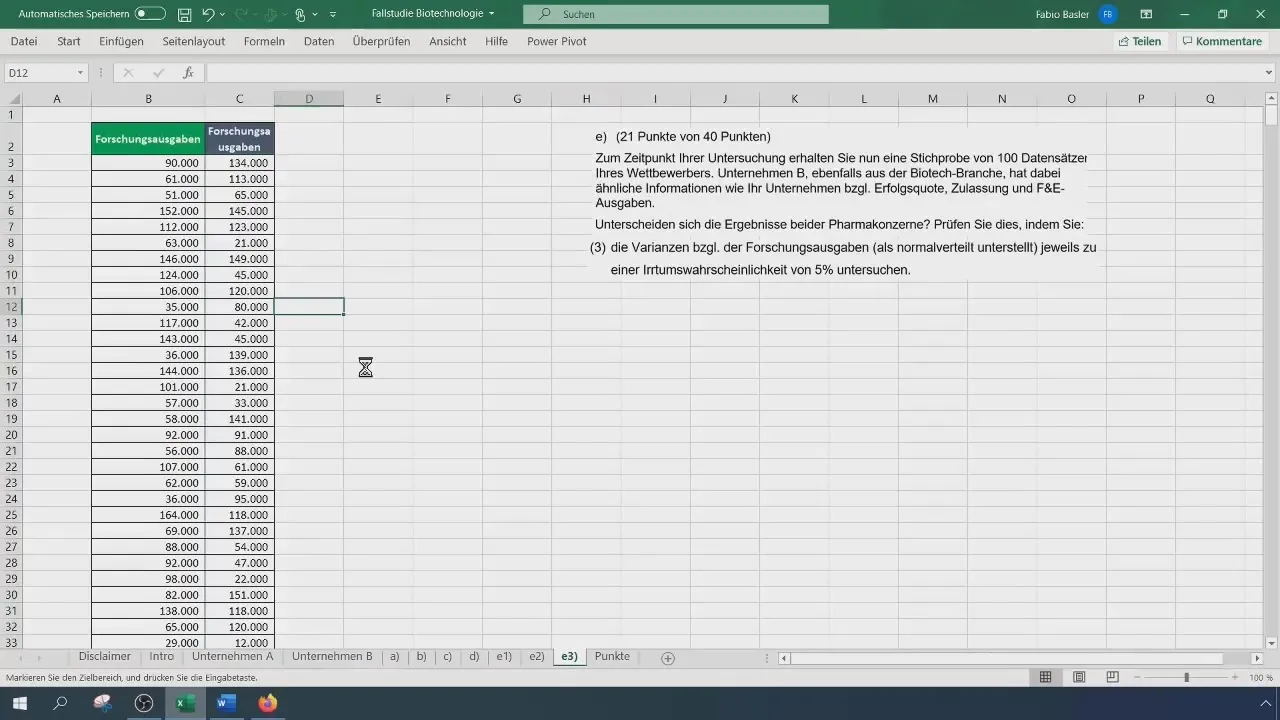
Étape 7 : Utiliser l'analyse des données Excel
Excel permet également d'effectuer le test F via la fonction d'analyse des données. Allez dans "Données" et sélectionnez "Analyse des données". Choisissez le "test F à deux échantillons". Entrez les plages des deux variables et sélectionnez les options appropriées.
Étape 8 : Interpréter les résultats
Analysez les résultats du test F. Si la statistique F calculée et la valeur p dans la sortie Excel donnent les mêmes résultats que votre calcul manuel, vous pouvez conclure que les variances des deux entreprises sont égales.
Résumé
Le test F à deux échantillons est un outil essentiel dans l'analyse statistique qui vous permet de comparer les différences de variance entre deux groupes. Dans ce guide, vous avez appris comment effectuer ce test de manière efficace dans Excel, de la préparation des données à l'interprétation des résultats.
Questions fréquemment posées
Qu'est-ce que le test F à deux échantillons ?Le test F à deux échantillons compare les variances de deux groupes pour déterminer s'ils sont statistiquement significativement différents.
Quand devrais-je utiliser un test F ?Un test F est utilisé lorsque vous souhaitez vérifier l'égalité des variances dans deux groupes indépendants.
Comment calculer la statistique F ?La statistique F est calculée en divisant la variance du premier groupe par la variance du deuxième groupe.
Que faire si l'hypothèse nulle est rejetée ?Si l'hypothèse nulle est rejetée, vous pouvez supposer que les variances des deux groupes sont statistiquement significativement différentes.
Y a-t-il des alternatives au test F ?Oui, vous pouvez également utiliser le test de Bartlett ou le test de Levene si vous souhaitez tester l'homogénéité des variances.


